2. 中国气象局, 北京 100081
2. China Meteorological Administration, Beijing 100081
预测电力负荷时考虑天气的影响, 对电力系统控制、运行和计划都很重要, 是电力市场有效运作的基础。准确的负荷预测可以使发电商和电网公司签订的预购合同更接近实际交易合同, 避免了因合同变更而产生的交易费用; 能够使电网公司在保证电网安全的前提下, 降低电网公司的运营成本; 能够为电力市场的投资规划提供决策依据。因此, 能源经济学家和能源电力企业对负荷预测很感兴趣, 研究天气变化与电力负荷变动, 特别是对短期负荷预测 (从几分钟到一周) 研究较多[1-2]。研究方法主要包括统计学方法、神经网络方法、模糊理论法、小波分析法、专家系统法等。研究中, 有些只考虑年平均温度序列, 没有包括季节性变动[3-4], 有些对较长时期 (季、半年) 的预测较弱。国内的研究主要集中在支持向量机方法和神经网络方法预测短期负荷[5-6], 以计量经济学手段预测月、季、半年的电力负荷研究尚不多见[7]。
本文以北京市2002-2004年气温和电力负荷数据为基础, 用计量经济学方法, 构建气温对电力负荷影响的数学模型, 检查北京市电力负荷与气温的关系。电力负荷受经济发展水平、能源结构、天气等多种因素的影响, 如何分离出气温因素一直是个难题。本文构造了气温的派生变量---采暖度日指数 (Heating Degree Days, HDD) 和制冷度日指数 (Cooling Degree Days, CDD), 充分考虑一周的每天、月份及节假日对电力需求的季节性影响, 较好地解决了这个难题。
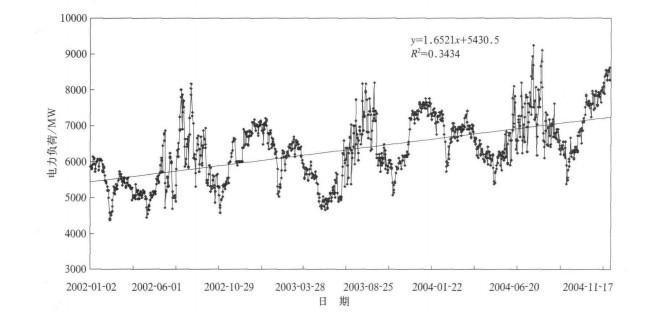
1 数据与资料本文使用的电力数据是北京市2002-2004年日最高电力负荷, 共1096个观测值。这些负荷包括农业、工业、服务业和居民等各部门的用电负荷, 分部门的用电负荷无法得到。由于样本观测值较多, 所以出现异方差的可能性较大[8], 异方差违背了回归分析的方差一致性假设。计量经济学中经常用取对数的方法消除异方差[9], 本文就使用这种方法。从图 1可以看出, 去趋势后的最高电力负荷与气温之间呈指数趋势, 取对数后可将指数趋势变为线性趋势。因此, 本文对最高电力负荷取自然对数, 用Lt表示。
|
|
| 图 1. 2002-2004年北京市日电力负荷 Fig 1. Beijing daily electricity load during 2002-2004 | |
过去的研究显示, 气温是影响电力需求的最显著变量[10]。本文选取北京市2002-2004年每日的室外气温T(单位:℃) 为影响电力负荷的影响因子, 尽管湿度、风速等对电力负荷也有影响, 但由于资料的可获得性等原因, 本文暂不考虑。室外气温数据来自北京市丰台气象站, 将每日最高气温与最低气温相加除以2计算得到每日平均气温, 即
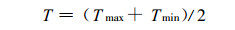
|
(1) |
Pardo等研究表明, 这种计算方法是无偏的, 随机误差不超过0.5 ℃[8]。本文所说的气温指日平均气温。
图 1是北京市2002-2004年的日电力负荷变动情况。电力负荷随着季节的变化而上下波动, 主要表现为夏季和冬季电力负荷增加, 春秋两季电力负荷减少。这显然与夏天制冷降温、冬天取暖有关。从图 1还可以看出电力负荷随时间增加的趋势, 这主要是由于经济发展引起的 (北京市GDP每年以超过10%的速度增长)。
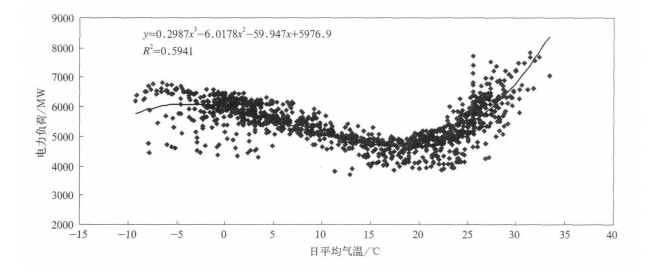
图 2显示出气温与电力负荷之间相关关系。值得说明的是, 图 2中电力负荷数据不是原始数据, 而是对原数据按图 1的线性增长率去趋势后的值。因为包含趋势的电力负荷数据与气温之间相关性并不明显。显然, 电力负荷与气温之间是非线性关系, 呈U型。气温高于某个阈值后, 电力需求随气温升高而增加, 气温低于这个阈值后, 电力需求随气温降低而增加。但是电力需求对高温和低温的敏感程度并不相同。当气温为25 ℃时, 气温上升1 ℃, 电力负荷增加3.7%, 当气温为30 ℃时, 上升1 ℃, 电力负荷会增加5.7%, 而当气温低于10 ℃时, 降低1 ℃, 电力负荷只增加1%~1.8%。主要原因是冬天的供暖方式多样, 北京以天然气为主, 电力供暖为辅, 而夏天只能用电力制冷。在18 ℃左右, 电力需求最低, 气温对电力负荷影响最小。
|
|
| 图 2. 2002-2004年北京市日平均气温与电力负荷 (去趋势) 散点图 Fig 2. Scatter diagram of daily temperature and electricity load (detrend) of Beijing during 2002-2004 | |
正如图 2所示, 气温对电力需求的影响是非线性的, 在这个U型曲线的两侧, 随着气温的升高 (降低), 电力需求都增加。因此需要把这两侧分开, 以分别描述气温升高和气温降低对电力需求的影响。国际上一般引入采暖度日指数和制冷度日指数两个温度派生指标, 这种分割有助于建立简洁的线性模型, 预测能力更强[8]。所谓度日就是指日平均气温与选定的参考温度的实际离差, 它反映冬天的冷和夏天的热的强度和持续的时间, 因而也可以反映能源需求的强度。HDD的值表示平均气温低于参考温度 (如18 ℃) 的大小, HDD越大, 表示气温越低, 需要采暖强度越大。CDD的值表示平均气温高于参考温度的大小, CDD越大, 表示气温越高, 需要制冷强度越大。HDD为零时, 表示气温舒适, 不需要采暖, 也不需要制冷。HDD, CDD均为非负数, 第t天的HDD, CDD计算公式如下:
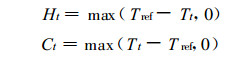
|
(2) |
式 (2) 中, Ht, Ct, Tt分别表示第t天的HDD, CDD, 平均气温; Tref为参考温度。参考温度的选择应以能分开冷热季节对能源电力的需求为原则。由图 2可以看出, 当温度为18 ℃左右时, 电力需求对温度的弹性最小, 正好是需要制冷和需要采暖的分水岭, 所以本文取Tref为18 ℃。模型中用到的HDD, CDD数据均由上式计算得到。不同的地区可以取不同的参考温度, 如北欧的斯堪的纳维亚国家和波兰取17 ℃, 美国取65 °F (相当18.3 ℃), 加拿大则与本文一致[11-13]。在建立模型过程中参考温度选择16~20 ℃, 但模型结果没有明显改进。
2 方法与模型 2.1 基本模型模型用到如下解释变量:
时间t。这个变量是用于描述电力负荷的长期趋势。这种长期增加的趋势主要与社会、经济、技术和人口等因素有关, 如城市化进程的加快, 生活水平的提高, 居民空调拥有量的增加, 以及人口的持续增加 (主要由于各种外来人口增加)。去除时间序列趋势的常用方法有两种, 一是差分, 二是引入时间变量多项式[9]。本文用后者, 并假设经济增长近似呈线性 (即一次多项式), 这样使模型相对简单, 而且也比较准确。即使对经济发展作更复杂的假设, 模型结果并不会有显著提高[14]。
第t天的采暖度日指数Ht和制冷度日指数Ct。
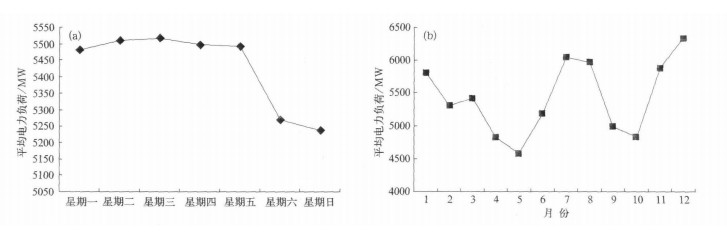
6个星期虚拟变量Dit, 它们代表一周内的每天电力需求变化。i=2, 3, …, 7, 分别代表星期二, 星期三, …, 星期日。星期一为基础日。当然任何一天都可以作为基础日。虚拟变量是定性变量, 当定性变量有m个类型时, 模型不能引入m个虚拟变量, 否则在虚拟变量间会产生完全多重共线性[9]。每个虚拟变量只能取值1或0。例如, 如果第t天为星期二, 则D2t=1, 其他Dit=0;如果第t天为星期三, 则D3t=1, 其他Dit=0, 以此类推。如果第t天为星期一, 则所有的Dit=0。研究表明, 一周内的每天电力需求变化有较强的周期性[15], 比如星期一到星期五用电量比较大, 而非工作日的星期六和星期日用电量比较小 (如图 3a所示), 因此引入星期虚拟变量可以捕捉这种非温度引起的电力负荷变化。
|
|
| 图 3. 2002-2004年一周 (a) 及各月 (b) 平均电力负荷 Fig 3. Weekly (a) and monthly (b) fluctuation of average electricity load during 2002-2004 | |
11个月份虚拟变量Mjt。它们代表由于经济、社会等非温度因素引起的电力需求月份季节性变动, 如某些食品工业在节假日前用电量会增加, 学校等机构在暑假期间用电量会下降。电力负荷月度波动如图 3b所示。类似于星期虚拟变量, 月份虚拟变量Mjt的下标j=2, 3, …, 12, 分别代表2月, 3月, …, 12月, 取值情况也完全类似于上面的星期虚拟变量Dit。1月为基础月份 (任何月份均可以做基础月份), j为1月时, 所有的Mjt均取0。
两个节日虚拟变量Jt, St。Jt代表元旦、五一国际劳动节、十一国庆节, 这些节日时间相对固定。在这些假期期间, Jt取1, 其他时间取0。St代表我国的传统节日春节, 相对公历而言, 时间是变动的, 在模型中找到相应的日期, 春节期间St取1, 其他时间取0。一般而言, 在节假日里工业和服务业的用电量下降, 所以设置这些虚拟变量以使模型更准确。
考虑上面所有因素, 首先给出第一个模型形式:
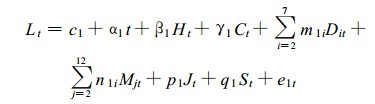
|
(3) |
式 (3) 中, c1, α1, β1, γ1, m1i (i=2, 3, …, 7), n1j(j=2, 3, …, 12), p1, q1为回归分析要估计的系数, e1t为随机误差项。
模型中引入了很多虚拟变量, 在这里有必要说明一下虚拟变量系数的含义。例如, 1月的非假期星期一的预期电力负荷为Lt=c1+α1t+β1Ht+γ1Ct, 而3月的非假期星期二的预期电力负荷为Lt=c1+α1t+β1Ht+γ1Ct+m1, 2+n1, 3。
依此类推。因而上面的模型就可以预测每天的电力负荷。
运用Eviews软件, 得到模型1的结果如表 1所示。常数项和趋势项非常显著, 两个气温派生指标也很显著, 且Ct的系数明显大于Ht的系数, 说明夏天气温升高比冬天气温降低对电力负荷影响更大些, 这与现实相吻合。星期一到星期五这几个虚拟变量的系数都是正数, 而星期六、星期日以及节假日的系数都是负数, 而且t检验非常显著, 说明非工作日的电力消费低于工作日。星期三的电力需求最高, 次低的依次是星期四、星期五、星期二。工作日t检验都不显著, 说明各工作日相对星期一来说, 电力负荷增加不明显。各月相对1月来说, 电力负荷有增有减, 3, 7, 8月t检验不显著。方程拟合优度87.1%, 不是很高。
|
|
表 1 模型1、模型2、模型3的估计结果 Table 1 Result of model-1, model-2 and model-3 |
2.2 序列相关
从模型1计算的DW统计量值看, 方程误差项存在严重正自相关。根据计量经济学理论, 如果误差项自相关, 则F检验和t检验的置信区间不是严格有效, 估计出的系数也是不稳定的, 有可能导致错误的结果。因此, 应该进一步优化模型。
解决序列相关的方法之一是把被解释变量的滞后项作为解释变量。本文考虑将Lt-1加入到解释变量, 结果显示误差自相关消除, 调整的拟合优度达95%, 似乎是个好模型。但是, 采暖度日指数Ht和制冷度日指数Ct的滞后项系数均为负值, 说明当天的高温或低温会引起第二天的电力需求下降, 这无法解释现实情况。星期虚拟变量系数Dit也为负。导致这种结果的原因是Lt-1对电力负荷Lt的解释力太强, 将本应由HDD, CDD等因素来解释的部分也包括了, 才导致了这种不合理现象。本文舍弃了这种消除序列相关方法。
解决序列相关的另一种方法是引入误差自回归结构 (AR)[15]。这种方法假设误差et可由有限期的误差滞后项来解释, 可表示为:
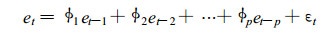
|
(4) |
即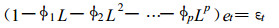
其中, L为滞后算子; φ1,φ2, …, φp是常系数, 在模型中需要估计; εt是白噪声过程。
有很多诊断方法以确定自回归结构, 本文以赤池信息准则 (AIC) 和许瓦兹准则 (SC) 值最小为原则, 确定了二阶自回归结构AR (2)。完整模型形式为:
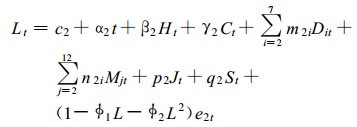
|
(5) |
模型2的回归分析结果在表 1中给出。可以看出, 调整的拟合优度 (R2) 大幅提高到95%, 说明模型的预测能力有很大提升。DW值为2.02, 自相关消除。常数项和趋势项仍然非常显著, 且系数有轻微增加。Ht和Ct系数有所下降, 这也说明增加AR的重要性。节假日与星期六、星期日的系数仍为负数, 说明电力需求在节假日减少。
2.3 模型动态化上述模型没有包括度日指数的动态结构, 事实上, 当天的气象条件 (尤其是气温) 对后几天的电力需求是有影响的。由于建筑物的隔热作用, 室外气温的变化不会立即影响室内温度, 室内温度调节对室外气温有一定滞后[16-17]。这说明Ht, Ct除对当天的电力负荷有影响外, 还存在滞后效应。为检验这个假设, 在模型2中引入Ht, Ct的二阶滞后变量Ht-1, Ct-1, Ht-2, Ct-2(三阶以上的滞后变量不显著, 对模型结果没有改进)。误差项的自回归结构仍按AIC, SC最小原则, 取AR (3)。新的模型3形式为:
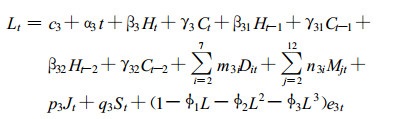
|
(6) |
模型3的回归结果见表 1。方程左侧是电力负荷的自然对数, 右侧是各解释变量的一次线性多项式。对方程求全微分, 则方程左侧等于电力负荷的增长率, 右侧为各变量的系数。因此各系数的值可以解释为:当解释变量变动一单位时, 电力负荷的变动率。主要结果如下:
度日指数Ht, Ct仍然显著, 且比模型2的相应系数略大。
Ct比Ht系数大, 说明夏季高温对电力负荷的影响比冬季低温更大。当CDD增加1 ℃时, 电力负荷增加1.962%, 即当平均气温超过18 ℃时, 每增加1 ℃, 电力负荷增加约2%。而如果是冷季, 气温每降低1 ℃, 电力负荷增加0.41%。
Ht-1, Ht-2小于Ht, Ct-1, Ct-2小于Ct, 说明度日指数对当天的电力负荷影响较大, 而对后几天的电力负荷影响较小。当天CDD增加1 ℃, 今后两天电力需求约增加0.33%~0.468%。当天HDD增加1 ℃, 今后两天电力需求约增加0.17%~0.19%。Ct-1不显著。
非工作日虚拟变量的系数均为负数, 而且显著, 说明非工作日的电力消费低于工作日。从D6和D7的系数可以看出, 星期六和星期日的电力需求比星期一分别下降3.14%和3.697%。而“五一”、“十一”等假日的电力负荷比非假日下降3%, 我国的传统节日春节期间, 电力需求减少6.375%。
除5, 6月虚拟变量系数显著外, 其他都不显著, 说明由于经济、社会原因影响的各月电力负荷 (非温度因素, 温度因素包含在度日指数中) 与1月没有明显的区别。4-8月系数为负, 可以解释为高温天气对社会经济有抑制作用, 导致用电负荷相对1月稍低。
调整的拟合优度达95.3%, 比模型2稍有提高。
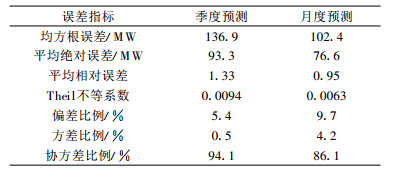
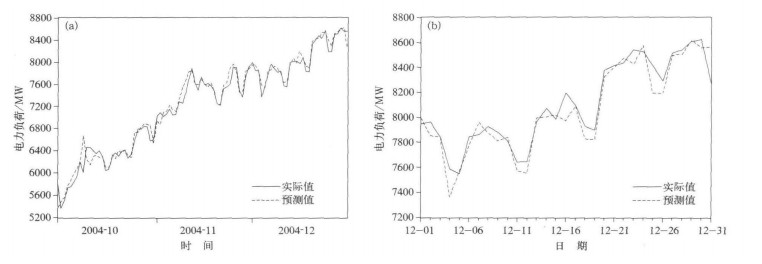
3 模型评估为了评估模型3的预测能力, 将2002-2004年的气温和电力负荷数据分成两部分, 一部分用于训练模型3, 另一部分用于预测。在模型评估中, 分别进行了季度和月度电力负荷预测。在季度预测中, 将2001年1月-2004年9月的数据用于训练模型3, 2004年第4季度的温度数据用于预测这季度的电力负荷。在月度预测中, 把2001年1月-2004年11月的数据用于训练模型3, 2004年12月的温度数据用于预测这个月份的电力负荷。有必要说明的是, 由于观测样本数减少, 所得到的变量系数与表 1中的模型3系数可能稍有不同。预测结果如图 4所示。
|
|
| 图 4. 2004年第4季度 (a) 及12月 (b) 电力负荷 Fig 4. Electricity load of the 4th quarter (a) and December (b) in 2004 | |
|
|
表 2 季度和月度预测误差 Table 2 Quarterly and monthly forecasting error |
从这些误差指标看, 模型预测能力较强。季度预测的偏差比例, 即预测均值与实际均值的偏离程度, 也即系统误差只有5.4%。均方根误差为136.9 MW, 即99.7%的概率保证误差不超过400 MW。月度预测也有类似的结果, 但从偏差比例看, 月度预测比季度预测的效果差。这些说明模型有较强的中期预测能力。由于只有3年的数据样本, 预测结果有一定偏差。如果增加样本数, 模型的预测能力会更好。国外的同类研究表明, 如果用10年的样本进行预测, 平均误差小于1%[15]。但应该注意的是, 这个误差评估是以实际温度来检验的。在实践中, 月度和季度气温预报的准确性往往不太理想, 这将对电力负荷的预估将产生重要影响。因此, 实践应用时, 要特别注意气温预报的准确性问题。
4 小结气象条件对能源电力消费的影响比较明确, 但由于气象条件的复杂性以及社会、经济、技术和人口等多种因素共同对电力消费发生作用, 使得预测电力消费极为复杂。本文以气温派生变量度日指数为解释变量, 引入序列相关AR结构和解释变量的动态结构, 以星期虚拟变量、月份虚拟变量和节假日虚拟变量来分解电力负荷的日、月和假期的季节性波动, 通过逐步优化的方法构建了气温与电力负荷的计量经济模型。模型结果很好地解释了气温变动、工作日与非工作日对电力需求的影响。
从模型估计看, CDD对电力负荷的影响比HDD大, CDD增加1 ℃, 电力负荷约增加3%, 而HDD增加1 ℃, 电力负荷约增加0.4%。CDD的滞后影响也比HDD的滞后影响大。星期六、星期日、“五一”等假日的用电负荷比正常情况 (工作日) 下降3%~4%之间, 而春节期间的用电负荷比正常情况下降更多, 超过6%。
对模型预测能力进行评估发现, 该模型季度预测的系统误差约为5%, 而月度预测的系统误差约为10%, 说明该模型有较好的中期预测能力, 对电力企业电力调度与电力建议有重要参考价值。
| [1] | Lotufo A D P, Minussi C R. Electric Power Systems Load Forecasting: A Survey. Paper BPT99-028-25 Accepted for Presentation at the IEEE Power Tech'99 Conference. Budapest, Hungary, 1999. |
| [2] | 张文哲, 陈刚. 电力市场下负荷预测综述. 渝西学院学报 (自然科学版), 2003, (3): 71–74. |
| [3] | Kermanshahi B, Iwamiya H, Up to year 2020 load forecasting using neural nets. Electrical Power Energy Syst, 2000, 24: 789–797. |
| [4] | Ringwood J V, Bofell D, Murray F T, Forecasting electricity demand on short, medium and long time scales using neural networks. J Intell Rob Syst, 2001, 31: 129–147. DOI:10.1023/A:1012046824237 |
| [5] | 艾名舜, 马红光, 刘遵雄. 基于RBFNN的短期电力负荷混沌局域预测法. 继电器, 2006, (14): 21–23. |
| [6] | 赵宇红, 唐耀庚, 张韵辉. 基于神经网络和模糊理论的短期负荷预测. 高电压技术, 2006, (5): 45–47. |
| [7] | 陈春琴. 数理统计分析在电力企业负荷预测中的应用. 华东电力, 2006, (5): 63–65. |
| [8] | Pardo A, Meneu V, Valor E, Temperature and seasonality influences on Spanish electricity load. Energy Econ, 2002, 24: 55–70. DOI:10.1016/S0140-9883(01)00082-2 |
| [9] | 张晓峒. 计量经济学基础. 天津: 南开大学出版社, 2001. |
| [10] | Li X, Sailor D J, Electricity use sensitivity to climate and climate change. World Resour Rev, 1995, 7, (3): 334–346. |
| [11] | Wibig J. Heating Degree Days and Cooling Degree Days Variability in Lodz in the Period 1931-2000. Fifth International Conference on Urbun Climate. Lodz, Poland, 2003:471-474. |
| [12] | Byrd G P, An adjustment for the effects of observation time on mean temperature and degree-days computations. J Clim Appl Met, 1985, 24, (8): 870–874. |
| [13] | 谢庄, 苏德斌, 虞海燕, 等. 北京地区热度日和冷度日的变化特征. 应用气象学报, 2007, 18, (2): 232–236. |
| [14] | Lalas D P, Mirasgedis S, Sarafidis Y, et al. Impacts of Environmental Restrictions on the Structure of the Electricity Sector. Technical Report Prepared by National Observatory of Athens for the Greek Public Power Corporation, Lofos Nimfon, Thission, 11810 Athens. 2003. |
| [15] | Mirasgedis S, Sarafidis Y, Georgopoulou E, et al. Models for mid-term electricity demand forecasting incorporating weather influences. Energy, 2006, 31: 208–227. DOI:10.1016/j.energy.2005.02.016 |
| [16] | Peirson J, Henley A, Electricity load and temperature:issues in dynamic specification. Energy Econ, 1994, 16, (4): 235–243. DOI:10.1016/0140-9883(94)90021-3 |
| [17] | Le Comte D, Warren H E, Modeling the impact of summer temperatures on national electricity consumption. J Appl Met, 1981, 20: 1415–1419. DOI:10.1175/1520-0450(1981)020<1415:MTIOST>2.0.CO;2 |
 2008, 19 (5): 531-538
2008, 19 (5): 531-538