2. 国家气象中心, 北京 100081
2. National Meteorological Center, Beijing 100081
在过去的十多年中, 国家气象中心利用多元回归的动力统计(MOS)[1]、卡尔曼滤波[2]、神经元网络[3-4]等统计方法和一些动力诊断方法[4]对数值预报产品进行释用, 已经取得了一定成绩, 使定时、定点、定量的要素客观预报无论在预报种类、或是在预报时效上都上了一个台阶, 预报质量也得到了较大提高。特别是对具有连续特点的要素, 如最高气温、最低气温及相对湿度的预报效果较好, 但是对于具有非线性特点的降水定量预报, 效果尚不够理想。由于某地发生的降水是大尺度环流与中小尺度系统相互作用的综合结果, 同时也是本地流场和热力场与当地地形、地貌有机结合的产物, 正是由于存在这样一系列复杂的物理过程, 因此, 目前对降水的定量预报除了依赖数值预报模式质量提高以外, 对数值模式产品的释用技术也提出了更高的要求。通常MOS、卡尔曼滤波等方法是假定观测数据误差服从一种概率密度分布, 并且输入的变量统计独立[5], 对于定量降水这样复杂多变且还没有完全认识的大气系统中取得的数据, 不能完全满足这些假设, 因此用这类统计方法建立的模型必然会影响预报的准确性和稳定性。近年来, 不少气象工作者在预报方法和预报技术的各环节上都进行着不断地改进, 如刘爱鸣等[6]利用滑动分区切比雪夫展开方法, 求取高度场特征分布的展开系数及其时间变量, 通过相关分析, 从中提取物理意义明确和相关性好的预报因子集和消空因子集, 再通过预报因子的多形态组合分析, 提炼出物理图像清晰的福建省前汛期区域暴雨预报模型。岳彩军等[7]用湿Q矢量散度场强迫的方程得到垂直速度, 再结合水汽条件进行降水量预报, 形成定量降水的动力释用方法。此外, 在预报对象的处理上也提出一些改进的办法, 如赵声蓉等[8]在对降水量进行分级预处理时, 将相对湿度与降水量结合形成新的实况因子; 陈力强等[9]首先对有无降水进行判别, 然后对降水量开4次方, 使预报对象尽量接近正态分布, 从而改善多元回归的效果。总之社会对要素预报的需求, 加之数值预报不完善的现状, 迫使数值预报产品的释用技术向更广、更深、更细的方向发展。
KNN(K-nearest neighbor)非参数估计技术[10]也是近几年来在数值预报释用中颇为重要的一种方法, 它是基于范例进行推理的人工智能领域中发展较快的一种求解问题技术, 是利用过去的范例或经验来解决当前问题的类比推理方法, 亦称为相似方法。为了解决降水和风的预报问题, 有人采用K近邻非参数估计技术, 这一方法不需要建立预报方程, 去除建立预报方程需要作的种种假设, 避开了需要参数估计的一些统计方法的弊病。翟宇梅等[11]提出了一种概率天气预报的K近邻非参数估计仿真模型(简称KNN-M), 利用该模型进行了降水和云量的概率预报试验, 得到较好的应用效果。邵明轩等[12]设计和试用了一种根据过程相似性从历史样本集中搜索出近邻子集, 并从新的近邻子集中挑选最佳样本的方法。经过业务试用, 该预报方法不仅使得风的预报TS评分有一定的提高, 同时使得72 h降水量的预报TS评分也有一定的提高。
KNN方法作为一种非线性模式识别分类器, 它的原理是通过将现有数据与已经存在的模板相匹配, 当找到匹配的模板时, 就把模板的类别当作需要识别物体的类别, 这符合人类认知事物的过程。由于气象要素样本较长, 并且获取资料较为及时, 这使得KNN技术得以在天气预报, 特别是在定性要素的判别中发挥作用。K近邻非参数估计技术中的关键是采用何种原则搜索出近邻子集, 以及如何从近邻子集中做出未来天气预报。在过去使用中, 对于历史样本数据集, 通常不考虑预报对象出现与不出现的样本数多寡, 特别是对小概率事件的天气, 如强降水, 显然两者的样本数悬殊很大, 如不考虑这一差别, 都使用同一K值作为邻域, 将会影响到最相似样本取舍的效果。该文针对降水预报提出一个改进的KNN客观方法, 其中分别考虑两类不同天气的历史样本, 同时通过交叉检验, 寻求客观有效地确定K值, 并利用这一方法制作了不同地区的降水预报试验, 对其结果进行分析与研究, 以此, 对降水的客观预报提供参考。
1 资料与加工利用2003-2006年4-9月国家气象中心逐日T213数值预报产品作为基本因子资料。所使用的T213数值预报产品包括15层7个预报时效(0, 12, 24, 36, 48, 60, 72 h)格点场中的14个基本气象要素, 包括:温度、高度、纬向风、经向风、垂直速度、比湿、相对湿度、海平面气压、地面温度、地面气压、10 m纬向风、10 m径向风、2 m温度、2 m相对湿度。利用这些基本气象要素通过动力诊断得出反映降水的如涡度、散度、位温等100多个气象物理量及如涡度、温度等平流项和梯度项物理量, 此外还有从地面到某层的垂直累积上升速度、水汽通量、水汽通量散度和一些时间累积的物理量, 然后利用双线性插值方法将这些基本要素和扩充物理量插值到对应的站点上, 建立起所需要的站点因子库。值得注意的是, 过去的工作都是寻求格点物理场的相似, 本研究尝试将格点场的资料直接插值到站点上, 一方面可将其与降水有关的物理量一并考虑, 另一方面也大大增加了可挑选的因子信息量。
实况数据集是采用MEOFIS系统[13]中的历史实况库, 取2003-2006年逐日08:00(北京时, 下同)到次日08:00的24 h降水量。
2 因子的选择因子的好坏直接影响着预报的效果, 因子较少不能概括预报对象信息, 因子较多又会有很多噪音干扰, 在众多因子中客观地选出较好的因子可以提高预报效果。首先确定某站点的预报对象, 而后计算该站预报时效所对应的T213模式(可跨前后1~2个时效)的预报因子与相应预报对象之间的相关, 从而挑选出一批与预报对象相关系数较大的不同层次的各种因子。然后再通过逐步回归的方法, 经过F检验在这批因子中选取其中关系最好的10~20个左右的因子, 形成该站点的预报因子集。对不同的站点, 不同的时效以及不同的预报对象来说, 所选出来的因子和因子个数是不一样的。对于某一站点, 某一降水量等级, 某一预报时刻来说, 把这些因子对应的样本选出作为模型文件, 计算预报场的因子(与模型相同)与历史资料因子间的距离, 通过交叉验证的KNN方法进行预报。
另外由于预报因子之间量级的差异, 在建模之前, 使用式(1)对全部样本的每一个因子分别做归一化处理, 使每个因子的数据在[0, 1]之间。
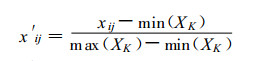
|
(1) |
式(1)中, x′ij为标准化后因子值; xij为标准化前的因子值; i为样本数; j为因子数。min(XK)和max(XK)分别表示第K个因子的所有样本中的最小值和最大值。
3 KNN方法的改进和参数选取 3.1 KNN原理KNN方法可以做如下表述, 给定一组历史训练样本集:
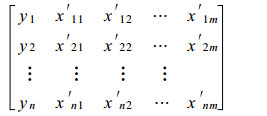
|
(2) |
式(2)中, x′ij ∈ R, i=1, 2, …, n; j=1, 2, …, m; n为样本数, m为因子数, x′ij是数值预报产品挑选出来的因子标准化后的值, yi ∈ { 1, 0}, 为预报对象(某天气实况)集, 其中0代表没出现该天气事件, 称这类样本为负样本, 1代表出现该天气事件, 称这类样本为正样本, 它们都是来自历史的实况资料库。
另外给出待预报数据集
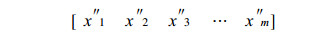
|
(3) |
式(3)中, x″j ∈ R, j=1, 2, …, m; 是与历史训练样本集中的因子相对应的实时预报数据样本。
计算待预报数据样本与历史数据样本中对应的每个子样本的距离, 这里采用欧式距离作为相似判据:

|
(4) |
式(4)中, Di ∈ R, i=1, 2, …, n; 这样n个样本数可得到n个距离, 按距离依次排序, 选择第K个作为待预报数据的判断标准, 凡小于该距离的样本, 就作为待预报的最近邻域。通过统计训练样本中小于判别距离DK的个数, 将预测数据集的类别归到其中个数较多的一类中, 从而做出预报。
3.2 分类求取K值对于有无降水、有无中雨或有无大雨等这两种类型的天气样本数是不均衡的, 特别对于北方地区, K值大小对邻近域有着直接的影响, 也是相似预报效果好坏的关键。通过试验发现, 在同一个训练集中, 对于正负两类子样本采取不同的K值的预报效果, 要比对正负样本都用同一个K值的预报效果要好。下面对分类算法描述如下:
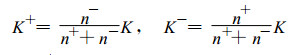
|
(5) |
式(5)中n+为训练样本中的正样本数(如有雨天数), n-为训练样本中的负样本数(如无雨天数)。K+为正样本的K值, K-为负样本的K值。对于不同站点的正样本数根据自身在总体样本中的比例而确定K值, 使正负样本的K值具有不同的权重。这里假设在总天数中雨天日数少于无雨天日数, 式(5)左边公式表示占据概率较小的天气类(如雨天)取的K值权重较大, 增大这类小概率事件的天气的最近邻域K+值, 而式(5)右边公式表示占据概率较大的天气类(如无雨)取的K值权重较小, 使其减少最近邻域K-值。通过这样处理, 将KNN方法选择的最邻近域中的K值取得更为合理。
由于K值分为两个部分, 那么K+和K-就分别对应不同的距离(DK+, DK-)。通过统计小于DK+距离的正样本数和小于DK-的负样本数, 比较两者样本数的大小, 把将预测的对象归到样本数目较多的一类天气事件, 从而做出预报。
3.3 交叉验证求取最佳K的组合搜索近邻的过程就是根据事先定义的相似性测度, 在历史数据库中寻找和当前预测状态条件特征相似的历史记录, 并把搜索到的有相似特征的历史记录标记为一个近邻, 所有搜索到的近邻就组成了近邻子集。最优近邻子集是指那些在搜索得到的所有近邻中对预报矢量估计贡献最大的近邻组合而成的子集, 一般由控制参数和一个最优化指标确定, 最优化近邻子集的过程是一个函数寻优过程。
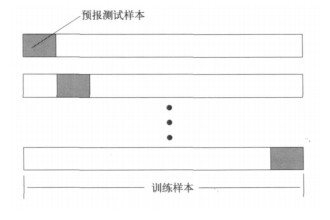
这里, 在K值的选择中, 首先确定某一K值(如从K=1开始), 然后利用交叉验证的方法, 取训练样本中的一部分作为试预报称为预报测试集, 将剩余部分作为训练样本集, 通过不断的交叉更换预报测试样本(图 1), 直到遍历整个样本集为止。至此, 将每次预报的结果汇集并进行检验, 得到一组评分结果。再改变K值, 重复上述过程, 得到另一组检验评分结果, 这样依次下去, 直到K值试验完毕(如K=50为止)。
|
|
| 图 1. 交叉验证示意图 Fig 1. The sketch map of cross validation | |
对于上述逐个预测结果采用4种评价标准, 分别是准确率(全体样本), 以及正样本的概括率、TS评分和空报率:

|
(6) |

|
(7) |

|
(8) |

|
(9) |
式中, 空报指预报为正类但实际是负类; 漏报指预报其中, 预报判别值是通过历史资料试预报比较判断给出。制作预报时, 当由式(12)计算出来的预报判别值大于该给定值, 则认为有该类天气事件发生, 反之则无。
为了更清楚具体步骤, 对以上所述KNN方法流程归纳如下:①提取数据, 求解相关系数, 利用逐步回归对因子进行筛选, 选出10~20个因子作为KNN的预报因子集; ②循环K值(比如从1~50, )利用式(5)将K值分解为K+, K-; ③在每一次K值循环中, 把模型样本分为与预报测试样本和训练集样本, 通过不断的交叉提取, 计算每个预报测试样本中的DK+, DK-, 做出每一个子样本的预报, 将交叉所得的预报结果汇集起来, 而后得出该K+, K-值所对应的预报评分; ④最后通过式(10)和(11)选出最优的K+, K-值; ⑤对历史资料由确定的K+, K-值, 寻求最邻近域, 通过预报判别式(12)确定预报判别值; ⑥预报时, 用确定的K+, K-值计算实时预报因子与历史样本的最邻近域, 并以预报判别值为标准, 最后给出预报结论。
4 试验结果分析利用2003-2005年4-9月的T213资料以及实为负类但实际为正类。
为了达到较好的预报效果, 既要考虑总体样本的准确率, 又要考虑正样本的概括率或TS评分。这里, 为减少漏报率, 着重考虑准确率和正样本的概括率, 提出如下K值选择公式:

|
(10) |

|
(11) |
通过L次交叉验证后(L的大小根据具体样本的大小确定, 或者使用留一法确定L), 不断调整K+, K-两个值, 比较上述预报试验的评分结果, 选出准确率和正样本的概括率都达到相对最优的组合, 从而将该最优组合所对应的K+, K-作为最终选择。
实际预报中, 将某站点实时预报因子, 依据上述确定的K+, K-值, 从历史样本中选取最邻近域, 而后用以下预报判别的办法给出预报结论。其预报判别公式为:
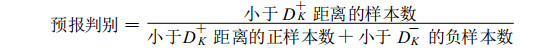
|
(12) |
况资料作为训练样本集, 通过KNN方法对2006年4-9月逐日08:00-08:00 24 h降水量进行24 h与48 h大于或等于0 mm晴雨预报和大于或等于10 mm降水预报试验。本文选取代表不同地域的14个气象站点(包括:沈阳, 青岛, 郑州, 安康, 武汉, 南京, 合肥, 南昌, 河池, 漳州, 梧州, 汕头, 湛江, 三亚)进行试报。通过对不同站点, 不同预报时效(24, 48 h)以及不同降水量等级, 建立不同的参数与模型。这些建立出来的参数与模型对于同一站点, 同一预报时效, 同一降水量级在4-9月的每天预报中不会发生改变。
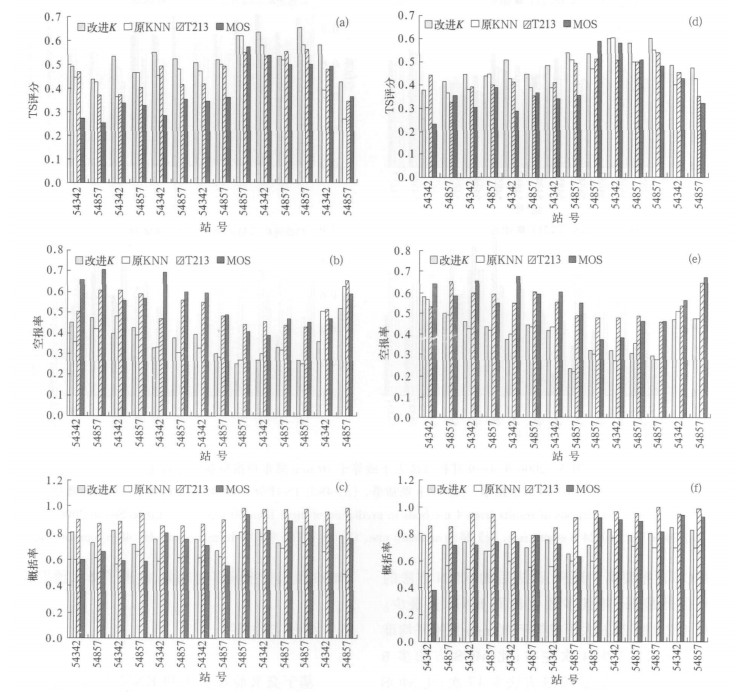
为了衡量改进后的KNN预报效果, 用传统的KNN方法和同样的数据对上述站点制作降水预报, 并将T213数值预报的逐日降水结果(将离预报站点距离最近的一个网格点上的预报值作为该站点的T213降水预报值)、以及通常用MOS方法的预报结果作为对比参照, 以此考察改进后的KNN预报方法是否具有实际应用的价值。对2006年4-9月预报结果检验如下:图 2为4种预报方法做出的24, 48 h晴雨预报的TS评分、空报率及概括率。从中不难看出:改进后的KNN方法对24 h晴雨预报的TS评分普遍高于其他方法, 其中安康、河池24 h改进后的KNN与原KNN的TS评分不相上下, 48 h还略低于后者, 除此之外, 改进后的KNN均高于原KNN。除了梧州24 h TS评分比MOS略低, 48 h TS评分沈阳比T213偏低, 河池比MOS偏低外, 其他都高于T213和MOS方法。24 h和48 h预报, 改进后的KNN空报率明显低于后两者, 14个台站的平均空报次数只有T213的40%, 这就使得预报的可信度得到很大提高, 但两种KNN方法相差不多。改进后的KNN比原KNN的正样本概括率高, 而比T213有所降低, 也有部分台站比MOS偏低的现象。改进后的KNN方法的14个站177 d的24 h雨天预报的平均准确次数比T213少10次, 但是平均空报次数比T213少36次。可见, 尽管概括率降低, 而空报明显减少, 有利于预报效果的提高。48 h晴雨预报平均准确的次数比T213少10次。比MOS方法少2次; 平均空报次数比T213方法少38次, 比MOS方法少30次。
|
|
| 图 2. 2006年4-9月各方法晴雨预报检验评分对比 (a)24 h TS评分,(b)24 h空报率,(c)24 h概括率,(d)48 h TS评分,(e)48 h空报率,(f)48 h概括率 Fig 2. Comparisons of results from 4 methods to prediction of 0 mm from Apr to Sep in 2006 (a)24 h TS,(b)24 h empty rate,(c)24 h summary rate,(d)48 h TS,(e)48 h empty rate,(f)48 h summary rate | |
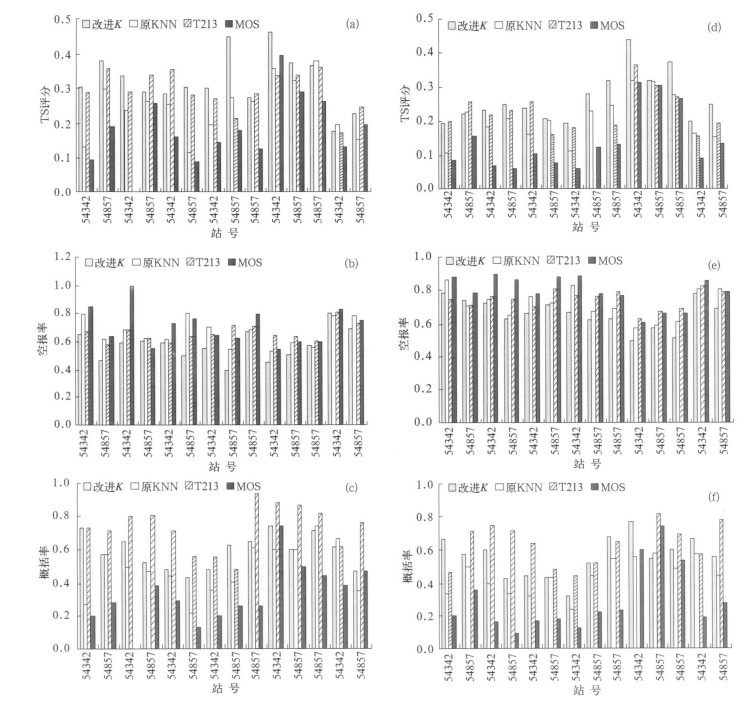
与晴雨预报类似, 对于大于或等于10 mm的预报(图 3), 两个时效(24, 48 h)除有2~3个站外, 其余站的TS评分均比T213高, 特别是24 h南昌和漳州高于T213达0.1以上, 并且所有站的TS评分都比MOS预报要高。同样, 改进后的KNN方法的空报率仍然最低, 并且多数也比原KNN空报少。14个站177 d的24 h大于或等于10 mm预报平均准确的次数比T213少4次左右; 比MOS方法多6次, 但平均空报次数比T213方法少17次; 比MOS方法少30次。48 h大于或等于10 mm预报平均准确的次数比T213少3次。比MOS方法多6次; 平均空报次数比T213方法少20次, 比MOS方法少2次。总体看来, 改进的KNN方法无论是24 h还是48 h预报, 均优于其他方法, 克服了数值预报和MOS预报空报偏多的现象, 改善了降水预报效果。
|
|
| 图 3. 2006年4-9月各方法大于或等于10 mm降水预报检验评分对比 (a)24 h TS评分,(b)24 h空报率,(c)24 h概括率,(d)48 h TS评分,(e)48 h空报率,(f)48 h概括率 Fig 3. Comparisons of results from 4 methods to prediction of more than 10 mm from Apr to Sep in 2006 (a)24 h TS,(b)24 h empty rate,(c)24 h summary rate,(d)48 h TS,(e)48 h empty rate,(f)48 h summary rate | |
5 结论与讨论
基于交叉验证技术的KNN方法用于T213数值预报模式产品的解释应用, 在客观、定点降水预报方面进行了初步尝试, 该方法主要特点如下:
1) 对不同站点, 通过求取相关系数和利用逐步回归方法, 从大量数值预报因子中提取不同层次、不同时效多个因子。与其他相似预报相比, 这无疑大大增加了利用数值预报结果的信息量。
2) 该方法仍以欧氏距离作为相似测度, 在搜索K邻近域的过程中, 考虑天气事件出现的概率不同, 分别求取正样本K+值和负样本K-值, 使最邻近K值的选择更为合理。
3) 利用交叉验证的方法依次选取部分样本作为预报测试集, 通过预测结果的检验评分, 选取获得最大准确率和最大概括率的K+值和K-值作为最佳邻近域的组合。
4) 确定了最优K值后, 反算历史样本, 通过比较, 得到该站该天气事件的预报判别值, 这在一定程度上减少了空报, 达到了较好的预报效果。
由于资料样本长度的限制, 本试验对降水预报没有分季节进行, 而事实上春季降水与夏季降水, 无论是环流背景、还是影响系统都有明显的差异, 对4-9月笼统提取同一组预报因子, 显然不十分合理, 进而也会影响预报效果。如果首先划分天气类型, 在不同的环流背景下分别选取因子, 将会反映不同天气特点的预报信息, 可能有助于选择更合适的邻近域, 以达到提高预报水平的目的, 这将是在下一步工作中需要改进的。
| [1] | 刘还珠, 赵声蓉, 赵翠光, 等. 国家气象中心气象要素的客观预报——MOS系统. 应用气象学报, 2004, 15, (2): 181–191. |
| [2] | 陆如华, 何于班. 卡尔曼滤波方法在天气预报中的应用. 气象, 1994, 20, (9): 41–46. |
| [3] | 林健玲, 金龙, 彭海燕. 区域降水数值预报产品人工神经网络释用预报研究. 气象科技, 2006, 34, (1): 12–17. |
| [4] | 刘还珠, 汤桂生. 暴雨落区预报实用方法. 北京: 气象出版社, 2000: 103-107. |
| [5] | 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 2000: 103-107. |
| [6] | 刘爱鸣, 潘宁, 邹燕, 等. 福建前汛期区域暴雨客观预报模型研究. 应用气象学报, 2003, 14, (4): 419–429. |
| [7] | 岳彩军, 寿亦萱, 寿绍文. 湿Q矢量释用技术及其在定量降水预报中应用研究. 应用气象学报, 2007, 18, (5): 666–675. |
| [8] | 赵声蓉, 裴海英. 客观定量预报中降水的预处理问题. 应用气象学报, 2007, 18, (1): 21–28. |
| [9] | 陈力强, 韩秀君, 张立祥. 基于MM5模式的站点降水预报释用方法研究. 气象科技, 2005, 31, (5): 268–272. |
| [10] | Cover T M, Hart P E, Nearest neighbor pattern classification. IEEE Trans on Inf Theory, 1967, 13: 21–27. DOI:10.1109/TIT.1967.1053964 |
| [11] | 翟宇梅, 赵瑞星. 概率天气预报的K近邻非参数估计仿真模型. 系统仿真学报, 2005, 17, (4): 786–788. |
| [12] | 邵明轩, 刘还珠, 窦以文. 用非参数估计技术预报风的研究. 应用气象学报, 2006, 17, (增刊): 125–129. |
| [13] | 车军辉, 李德生, 李玉华. 数值预报产品释用业务系统历史数据存储与检索. 应用气象学报, 2006, 17, (增刊): 152–156. |
| [14] | Bjarne K Harksen, Denis Riordan. Weather Prediction Using Casebased Reasoning and Fuzzy Set Theory. Master of Computer Science Thesis, Technical University of Nova Scotia, Halifax, Nova Scotia, Canada, 2001. |
| [15] | 郑烇, 王俊普, 蔡庆生. 一种基于时间范例的预测技术. 南京大学学报(自然科学), 2003, 39, (2): 159–164. |
 2008, 19 (4): 471-478
2008, 19 (4): 471-478

