应用气象学报  2008, 19 (4): 463-470   PDF    
引用本文
沈艳, 任芝花, 王颖, 刘小宁. 我国自动与人工蒸发量观测资料的对比分析[J]. 应用气象学报, 2008, 19(4): 463-470.
Shen Yan, Ren Zhihua, Wang Ying, Liu Xiaoning. Comparative Analysis on Automatic and Manual Evaporation Measurements in China[J]. Journal of Applied Meteorological Science, 2008, 19(4): 463-470  
我国自动与人工蒸发量观测资料的对比分析
沈艳, 任芝花, 王颖, 刘小宁     
国家气象信息中心, 北京 100081
2007-07-27 收到, 2008-01-03 收到修改稿.
资助项目: 国家级气象科学数据资源建设(2005DKA31700-02)和中国气象局气象新技术推广项目(CMATG2006Z03, CMATG2008Z12)共同资助    
摘要: 截止到2005年，全国共有130个台站进行蒸发量自动与人工业务观测。该文利用2005年平行观测月数据，对资料的差异和相关性以及比对系数和影响因子进行了讨论，结果表明：月蒸发量差值不满足正态分布，近80%的数据为自动观测值大于人工观测值；在人工观测值较小时，对应的自动与人工相对差值较大，随着人工观测值的增加，差值有减小趋势；自动与人工观测数据之间存在很好的线性相关关系，相关系数为0.98，通过了0.01的显著性检验；比对系数年平均值在1.0~1.2之间，两大高值中心分别位于广西都安和湖南南县；比对系数月平均值的变化近似于二次型拟合曲线，1月最大，6，7月最小；在定性讨论特征站比对系数影响因子的基础上，进一步查明了影响月比对系数的气象因子有月平均相对湿度和月平均风速。
关键词: 自动观测    人工观测    蒸发量    对比分析    
Comparative Analysis on Automatic and Manual Evaporation Measurements in China
Shen Yan, Ren Zhihua, Wang Ying, Liu Xiaoning     
National Meteorological Information Center, Beijing 100081
Abstract: Automatic Observation System (AOS) has been set up since 2002 and Manual Observation System (MOS) will be substituted gradually. The results show that data quality will be influenced by the changes of either the measurement instrument or the manner. So it is necessary to conduct AOS-MOS parallel observations to determine the discrepancy and correlation. For evaporation observations the difference is great between the manual and automatic observation. In fact manual evaporation is measured once a day at about 20:00, the difference of the two days measurements is the daily evaporation quantity. However, automatic measurements have been implemented to record continuously water surface height which is then used to calculate the hourly and daily evaporation at a given station. It is wanted by many meteorologists to know how much is the difference and the relationship between the amount of evaporation measured by automatic and manual observations and what is the main causes of the difference. There are 130 stations by 2005 conducting evaporation parallel measurements in China. The monthly or annual value is often used for evaporation analysis. Moreover the contrast coefficient is defined as the ratio between automatic and manual value and often used, too. Based on the monthly, annual value and contrast coefficient, various analyses are carried out on evaporation difference arising from two observation systems. The results are as follows: Monthly difference doesn't satisfy normal distribution pattern. The average monthly evaporation a mount observed by automatic way is 5.74 mm (or 5.51%) more than that by manual way. The standard deviation of the difference is 9.02 mm. In the 1050 evaporation comparison observations, 3.33% of data observed in the two ways is identical, 19.71% of data observed by automatic way is smaller, 76.95% of data observed by automatic way is larger. Namely, about 80% of automatic monthly data is greater than corresponding manual ones. Super sensitive of automatic ultrasonic probe and the measurement time discrepancy may be the reasons. When manual amount is small, its associated difference between automatic and manual is large, especially in the Wanyuan station in Sichuan Province. The monthly evaporation by automatic observation is obviously a linear function of that by manual one with the correlation coefficient passing 0.01 significant level test. The annual contrast coefficient is within the range of 1.0 to 1.2, with two high value regions centered at Douan and Nanxian stations in Guangxi and Hunan provinces, respectively. The change of monthly contrast coefficient is similar to bi-parabolic distribution pattern with highest and lowest value in January and June or July, respectively. Meteorological factors influencing the monthly contrast coefficient include the monthly average relative humidity and monthly average wind speed. There is a trend to merge the different kind of data to compose high quality evaporation dataset which deserves further research in the future.
Key words: automatic measurements     manual measurements     evaporation     comparative analysis    
引言

历史上任何观测仪器和观测方式的改变都会产生数据差异, 例如1980年以后, 全国陆续安装E-601型蒸发器代替小型蒸发器时, 就有专家对两种蒸发观测资料进行了对比分析[1]。随着我国气象观测自动化的发展, 自2002年以来, 陆续建立了地面气象自动观测站。自动站与人工观测之间的差异也是不可避免的。为了进一步明确两种观测资料间的差异及产生差异的原因, 中国气象局规定:地面自动气象站与人工必须平行观测至少两年, 在对两种观测资料进行质量评估并认为自动气象站可以单轨运行后再停止人工观测。平行观测期间降雨量的差异及相关性已有了较深入的讨论[2], 但对蒸发量的讨论未见报道。

蒸发是地面热量平衡和水量平衡的重要组成部分, 一直是国内外气象学、地理学、土壤学、水文学等相关学科关心的焦点问题之一, 已有大量的传统估算方法[3-6]和模拟估算法[7-11]。但蒸发量获取的根本途径就是直接观测[1]。国内原600多个基准基本站业务上是用WMO推荐的E-601型蒸发器来观测蒸发量的, 目前约130个站进行平行观测, 人工定点读数观测每日(20:00-次日20:00, 北京时, 下同)蒸发量, 自动观测由超声波蒸发传感器自动采集并计算出每小时和每日(20:00-次日20:00)的蒸发量。本文利用我国蒸发量自动与人工平行观测期数据, 在比较两者差异和相关性的基础上, 试图找出产生差异的原因。

1 蒸发量观测与数据 1.1 观测原理

E-601B型蒸发器由蒸发桶、水圈、溢流桶和测针等组成。每日20:00进行人工观测, 观测员会先调整测针针尖与水面恰好相接, 然后从游标尺上读出水面高度。人工观测计算蒸发量的公式是:蒸发量=前一日水面高度+降水量(以雨量器观测值为准)-测量时水面高度。自动观测是在同一蒸发桶内的专用三角支架上安装超声波传感器, 根据超声波测距原理, 利用高精度超声波探头, 对E-601B型蒸发器内水面高度变化进行连续检测, 转换成电信号输出。采集器能自动计算出每小时和1日(20:00-次日20:00)的蒸发量(会自动把同一时间内的降水量减去), 测量范围是0~100 mm, 分辨率是0.1 mm。若因降水使小时和日蒸发量出现负值时, 该值将按0.0 mm处理[12]。北方冬季结冰期停止观测。

1.2 观测数据

自动站观测的每小时蒸发量以及人工每日定时观测的资料均保存于地面气象观测数据A文件中[13], 并上传到各级资料部门。上传到国家气象信息中心的自动与人工蒸发量数据(A文件), 经过了台站维护以及各级质量检查, 其质量应优于两年平行观测资料。截止到2005年, 全国共有130个台站安装了蒸发量平行观测装置, 其中青海省(无人工蒸发量观测)和西藏地区暂无平行观测资料。影响日蒸发量的因素很多, 因此讨论蒸发量的变化一般都是基于月值和年值进行的[14]。对比分析前, 先对数据采用3倍标准差进行粗差处理, 在自动站观测的1109组月值资料中, 有18组作为了粗差数据, 粗差率为1.62%; 对应人工站的1074组月值资料中, 共有20组作为了粗差数据, 粗差率为1.86%。因此, 参加对比分析的月数据共有1050组。

需要说明的是:某些台站存在用自动观测日值数据代替人工观测日值的情况, 因此在分析过程中, 如果某台站1个月中连续10 d的人工观测日值等于自动观测日值, 则该数据不参加对比分析。定义了如下参数:

(1)
(2)
(3)

其中比对系数越接近1, 说明人工站观测的蒸发量越接近自动站测值。

2 两种资料对比分析 2.1 月蒸发量的差异和相关性 2.1.1 月蒸发量的差异

首先来检验自动与人工观测的月蒸发量差值是否遵从标准正态分布。在样本容量较大时, 假设月蒸发量差值遵从正态分布, 在0.05显著水平下, 若样本的峰度系数g1、偏度系数g2满足下式:

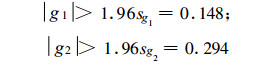
则拒绝假设, 变量不遵从正态分布[15]。其中, (n为样本容量)峰度系数g1、偏度系数g2的计算公式见文献[15]。

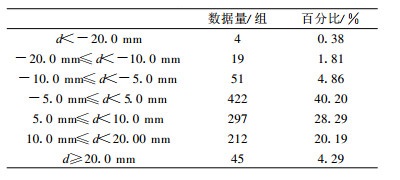
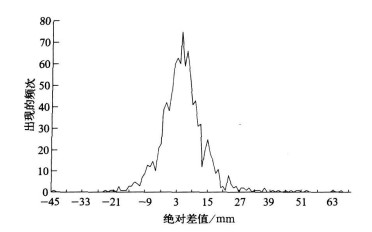
计算得到:|g1|=2.248, |g2|=15.332, 1.96sg1=0.148, 1.96sg2=0.294。在α=0.05的显著水平下, |g1| >1.96sg1, |g2| >1.96sg2, 假设不成立, 故自动与人工观测月蒸发量差值不遵从标准正态分布(均值为零, 方差为1)。但从月蒸发量绝对差值的频率分布(图 1)可见:最大频率出现在差值约5.0 mm处, 偏差过大和过小的概率明显减小, 是偏峰的准对称分布。这种偏峰的准对称分布主要是因为测量仪器不同造成的系统偏差。进一步对月蒸发量资料分析发现, 自动观测比人工观测的月蒸发量平均偏高5.74 mm, 相对偏高5.51%, 标准差为9.02 mm。在1050次有效对比观测中, 自动与人工观测月蒸发量一致的仅有35个占3.33%, 自动观测月蒸发量大于人工观测的有808个占76.95%, 自动观测月蒸发量小于人工观测的有207个占19.71%, 即3/4以上的台站自动观测值大于人工观测值。表 1详细列出了各差值段内的数据量及百分比, 其绝对差值在±5.0 mm的共有422组数据, 占数据量的40.20%, 其中有296组数据在0.0~5.0 mm之间; 而绝对差值在±10.0 mm的共有770组数据, 占73.35%。

图 1. 月蒸发量绝对差值的频率分布图 Fig 1. Frequency diagram of monthly evaporation difference in the parallel measurements

表 1 月蒸发量各差值段内的数据量和所占百分比 Table 1 Amount and percentage in every difference range of monthly evaporation

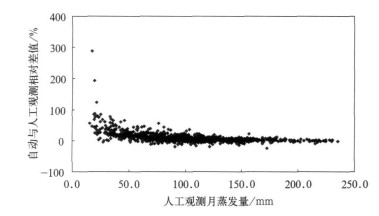
图 2显示了月蒸发量相对差值与人工观测月蒸发量的散点图。最大相对差值是289.5%, 最小为-25.5%; 人工观测的最大值是235.2 mm, 最小值是5.0 mm。从图中可见, 大部分月的相对差值均较小, 且随着月蒸发量的增加, 其相对差值有缓慢减小的趋势。但同时也注意到:相对差值较大的点, 往往对应人工观测的月蒸发量值较小, 其中最大相对差值289.5%对应的人工观测值为17.2 mm。自动与人工观测原理有别, 高精度超声波探头的优点是能很灵敏地感应水面高度变化, 然而受外界干扰也较大, 例如受蒸发池内湍流波动以及不明物体落入池中等许多不确定因素的影响。另外, 人工站20:00定时观测和自动站连续观测的时间不一致也会导致自动与人工观测的月蒸发量存在差异。

图 2. 自动与人工观测月蒸发量的相对差值与月蒸发量的散点图 Fig 2. Scatter plot between relative difference and monthly evaporation

2.1.2 月蒸发量的相关性

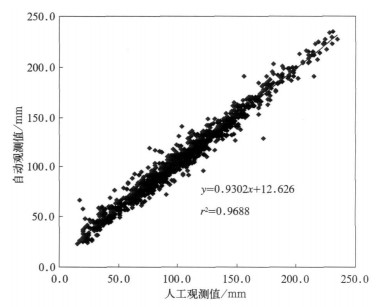
利用1050组有效对比观测数据进行了相关分析, 图 3即为自动与人工观测月蒸发量的相关关系图。可见, 数据分布近似围绕1:1直线, 二者观测的月蒸发量有很好的线性相关关系, 相关系数r为0.983, 通过了0.01水平的显著性检验。图中直线即为最小二乘法拟合的自动与人工测值的线性曲线, 其线性方程为:

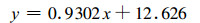
(4)

式(4)中, x代表人工观测的月蒸发量, y代表自动观测的月蒸发量。

图 3. 自动与人工观测月蒸发量的相关关系图 Fig 3. Correlation relationship between automatic and manual evaporation measurements

2.2 比对系数

比对系数可以反映两种资料差异的平均状况, 越接近1, 说明人工观测蒸发量越接近自动观测值。

2.2.1 全国平均变化特征

为了比较全国范围内自动与人工蒸发量观测资料的平均差异, 计算了各台站蒸发观测期的比对系数, 并据此生成了我国年平均比对系数等值线分布图(图 4)。从图 4可见, 总体上比对系数都大于1.0, 两大高值中心分别位于广西都安和湖南南县, 其中心值为1.2。另外, 黑龙江部分地区也是比对系数值较高的区域, 其他如内蒙古、新疆、华北平原以及东南沿海地区的比对系数大多维持在1.0或1.1, 而青海以及西藏暂无平行观测数据。

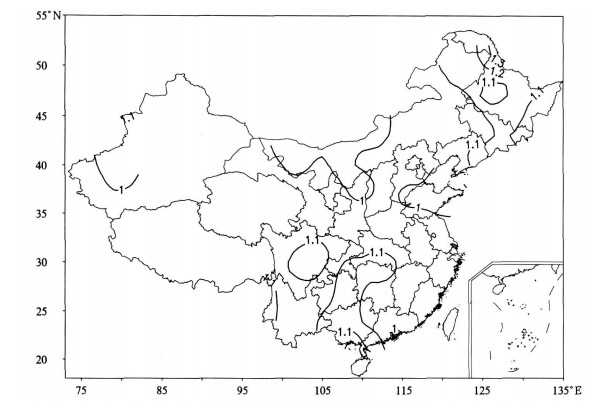
图 4. 我国蒸发量观测期间比对系数等值线分布图 Fig 4. Isoline map of contrast coefficient in China on the contrast of measurements

进一步绘制了比对系数各月平均值的变化曲线(图 5)。可见:1月的比对系数最大是1.49, 说明自动观测值约比人工观测值大一半; 而自动和人工观测差异最小的月份是6月和7月, 分别是1.08和1.09, 之后比对系数有所增加。用近似于二次型抛物线可以较好地模拟该变化趋势, 相关系数为0.96, 达到0.05显著性水平。该关系式只需要月份就能确定比对系数的月平均值, 对于长期进行人工蒸发量观测而暂无自动观测的台站, 利用该算式能方便的将人工观测值转换成自动观测值, 从而使全国蒸发资料具有更好的可比性。

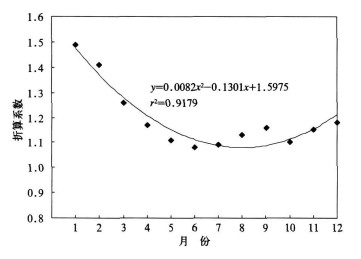
图 5. 比对系数月平均值的变化曲线 Fig 5. Monthly average curve of contrast coefficient

2.2.2 特征站的对比结果

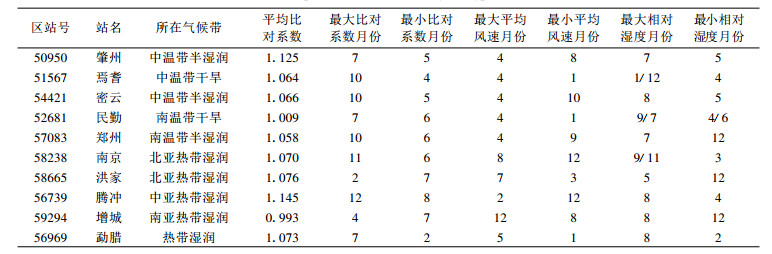
水面蒸发是一个受诸多因子影响的复杂物理过程。为了比较不同地区、不同季节、不同天气气候条件下自动与人工观测资料的差异, 选择了代表我国不同气候带的台站(表 2), 根据其月比对系数的变化(图 6)来定性探讨资料的差异。

表 2 不同气候带代表台站的比对系数及风速、相对湿度表 Table 2 Contrast coefficient and wind speed, relative humidity of typical stations at different climatic zones

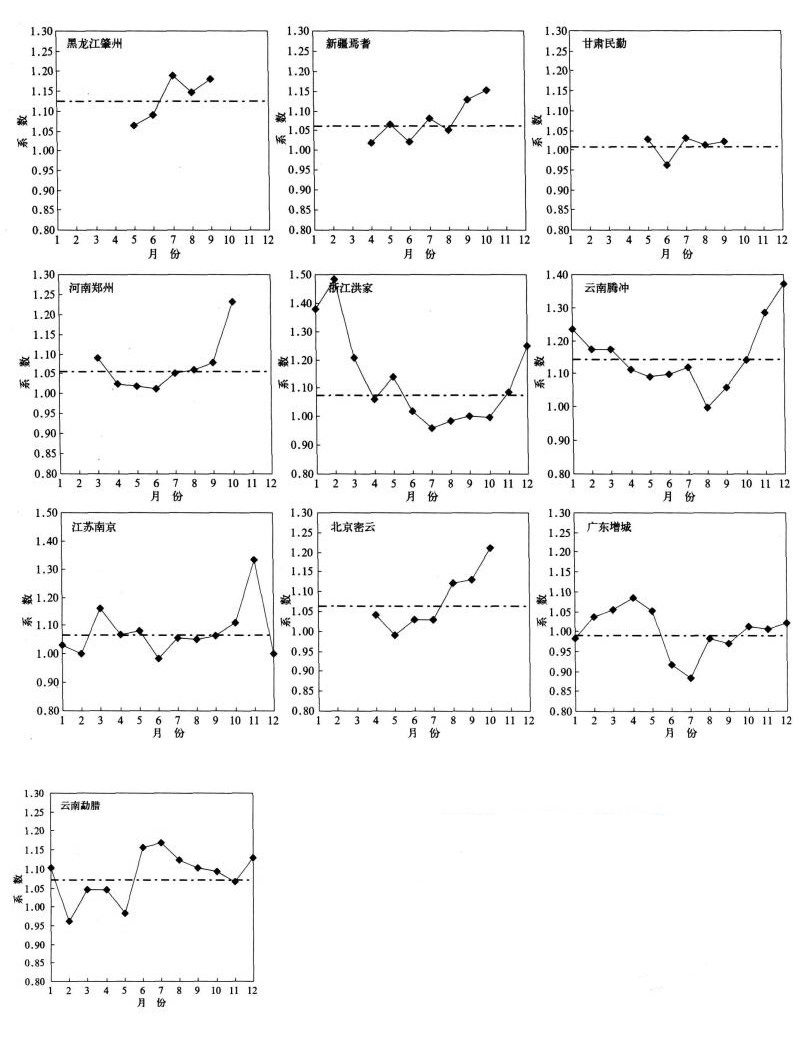
图 6. 各代表台站比对系数月变化曲线图 (全年观测的台站点划线表示年比对系数; 冬季停止观测的台站点划线表示各月平均比对系数) Fig 6. Monthly changing curves of contrast coefficient in typical stations (dash lines denote annual average contrast coefficient for all-year measured stations and monthly average parallel coeffient for winter-stopped measuring stations, respectively)

从图 6可以看出, 除了增城的年平均比对系数0.993小于1以外, 其他各站都大于1, 从1.009变化到1.145。说明我国自动站观测的蒸发量普遍大于人工观测值, 最小相对差值为0.9%, 最大相对差值达到14.5%, 平均相对差值是7.86%。另外, 从每条曲线的变化可以看出:代表各气候带不同天气特征下的比对系数, 其变化趋势不完全相同。如某些台站, 在降水多的月份, 其比对系数低于其平均值, 如腾冲站。受季风气候影响, 4-10月为该地区的雨季, 而对应各月的比对系数低于年比对系数, 甚至8月是比对系数最小值月, 与最大相对湿度出现的月份对应; 而其他月份高于年比对系数, 最大值出现在12月, 对应最小风速月。说明雨季人工站观测的蒸发量偏大(比对系数小), 而旱季人工站比自动站偏小(比对系数大)。增城站、洪家站、南京站以及郑州站的变化趋势均如此。尤其是洪家站, 其最小比对系数出现在7月, 正好对应最大风速月份。说明在这些台站, 人工观测值偏大受相对湿度和风速的共同影响较大。勐腊站、肇州站、密云站和民勤站比对系数的变化趋势正好相反, 这些站表现为雨季的比对系数大于平均值, 而旱季的比对系数小于平均值。对比表 2的结果, 这4个站比对系数最大值出现的月份与相对湿度有很好的正相关关系, 例如肇州站最大比对系数出现的7月恰好也是最大相对湿度出现的月份, 而最小比对系数在5月也正好是最小相对湿度出现的月份。说明在这些台站相对湿度是比对系数的主要影响因素。而焉耆站4-8月的比对系数波动变化, 其最小比对系数与最大平均风速和最小相对湿度出现的月份一致, 都是4月, 可以认为是相对湿度和风速综合作用的结果。

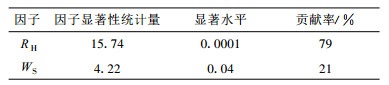
2.2.3 影响比对系数的主要气象因子

为了综合考虑月比对系数的影响因子, 共选入5个因子:月平均气温T、月平均最高气温Tmax、月平均最低气温Tmin、月平均相对湿度RH和月平均风速WS, 采用逐步回归分析方法[15]筛选因子并建立方程。在显著水平为0.05时, 入选的因子是WS和RH, 其结果见表 3, 对应的线性模型是:

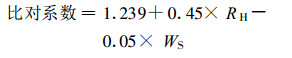
(5)

根据模型(5)中各系数的正、负号得到:月比对系数与RH成正相关, 与WS成负相关。而RH对比对系数的贡献率约是WS的4倍。从实用角度出发建立模型(5), 可为我国暂无蒸发量自动观测的台站用RH和WS估计比对系数提供参考。

表 3 逐步回归方法筛选因子结果及贡献率 Table 3 Selected factors by stepwise regression and its contributing ratio

3 小结与讨论

随着气象台站自动化水平的提高, 截止到2005年, 全国气象部门约有130多个台站蒸发量观测方式由人工定点读数观测每日(20:00-次日20:00)蒸发量, 变成了超声波蒸发传感器自动采集并计算出每小时和每日(20:00-次日20:00)的蒸发量。其仪器构造、观测原理、观测方式和计算方法均不同, 观测时次不一致、观测时间不同步等都会造成数据间的差异。本文利用2005年月蒸发量平行观测数据进行对比分析, 得到如下结论:

1) 月蒸发量差值不满足正态分布, 自动观测值比人工观测值平均偏高5.74 mm, 相对偏高5.51%, 标准差为9.02 mm。将近80%的数据都是自动观测值大于人工观测值。

2) 自动与人工观测月蒸发量数据间存在很好的线性相关, 相关系数达到0.98, 通过0.01的显著性检验。二者相对差值较大的站, 往往对应人工观测值较小。

3) 比对系数年平均值在1.0~1.2之间, 两大高值中心分别位于广西都安和湖南南县; 月变化近似于抛物线型, 1月最大, 6, 7月值最小。在定性讨论特征站比对系数影响因子的基础上, 进一步查明了影响月比对系数的气象因子有月平均相对湿度和月平均风速。由于进行蒸发量平行观测的台站数量较少, 数据序列较短, 加之北方冬季结冰期停止观测等原因, 因此分析是很初步的。相信随着序列的延长和蒸发自动观测站的增加, 必将促进对蒸发量的深入分析。

随着遥感反演技术的提高, 已有学者借助遥感图像计算了中国区域的蒸发(散)量[16-18]。但不可否认, 单纯利用遥感数据的反演精度常常不高, 其结果稳定性差, 受区域和时间的影响大。因此, 借助数据融合技术, 将遥感数据与地面观测数据有效结合, 是相关研究中值得深入的方向。

参考文献
[1] 刘小宁, 王淑清, 吴增祥, 等. 我国两种蒸发现测资料的对比分析. 应用气象学报, 1998, 9, (3): 321–328.
[2] 任芝花, 冯明农, 张洪政, 等. 自动与人工观测降雨量的差异及相关性. 应用气象学报, 2007, 18, (3): 358–364.
[3] Bowen I, The ratio of heat losses by conduction and evaporation from any water surface. Phys Rev, 1926, 27, (6): 779–787. DOI:10.1103/PhysRev.27.779
[4] Monteith J L, Environmental Control of Plant Growth. New York: Academic Press, 1963: 95-112.
[5] Hillel D, Applications of Soil Physics. New York: Academic Press, 1980.
[6] Lieth H, Whittaker R H, Primary Productivity of the Biosphere. New York: Springer Verlag, 1975.
[7] Dikinson R E, Changes in Land Use Climate System Modeling. Cambridge: Cambridge University Press, 1993: 689-701.
[8] Selles A H, Pitman J A, Land-surface schemes for future climate models: Specification, aggregation and heterogeneity. J Geophys Res, 1992, 97, (D3): 2787–2696.
[9] 裴步祥. 蒸发和蒸散的测定与计算. 北京: 气象出版社, 1989.
[10] 程维新. 农田蒸发与作物耗水量研究. 北京: 气象出版社, 1994.
[11] 谢贤群, 左大康, 唐登银. 农田蒸发———测定与计算. 北京: 气象出版社, 1991.
[12] 中国气象局. 地面气象观测规范. 北京: 气象出版社, 2003.
[13] 中国气象局. 地面气象观测数据文件和记录薄表格式. 北京: 气象出版社, 2005.
[14] 任芝花, 黎明琴, 张纬敏. 小型蒸发器对E—601B蒸发器的折算系数. 应用气象学报, 2002, 13, (4): 508–512.
[15] 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 2000.
[16] 马耀明, 王介民. 卫星遥感结合地面观测估算非均匀地表区域能量通量. 气象学报, 1999, 57, (2): 180–188.
[17] 陈云浩, 李晓兵, 史培军. 中国西北地区蒸发散量计算的遥感研究. 地理学报, 2001, 56, (3): 261–268.
[18] 郭建茂, 王连喜, 郑有飞, 等. 宁夏南部区域蒸发(散)量遥感估算方法. 南京气象学院学报, 2004, 27, (3): 302–309.