应用气象学报  2008, 19 (4): 454-462   PDF    
引用本文
陈廷娣, 王连仲, 窦贤康. TRMM卫星与机载雷达在降雨反演中的数据对比个例研究[J]. 应用气象学报, 2008, 19(4): 454-462.
Chen Tingdi, Wang Lianzhong, Dou Xiankang. A Case Comparison Between the TRMM Data and Airborne Radar Data in Rainfall Retrieval[J]. Journal of Applied Meteorological Science, 2008, 19(4): 454-462  
TRMM卫星与机载雷达在降雨反演中的数据对比个例研究
陈廷娣, 王连仲, 窦贤康     
中国科学技术大学地球和空间科学学院, 合肥 230026
2007-07-23 收到, 2008-01-22 收到修改稿.
资助项目: 国家自然科学基金面上项目(40275008)资助    
摘要: 热带降水测量卫星（TRMM）上搭载的测雨雷达是第一部能够提供三维降水信息的星载雷达，机载雷达也能够对降雨进行实时观测。由于机载和星载雷达观测有很多共同点，所以选择机载、星载雷达数据进行对比。1998年8月26日NOAA/P3飞机对Bonnie飓风进行了一次观测飞行，与此同时TRMM卫星也同步扫过该区域，因此利用对Bonnie飓风的机、星观测数据对应点数值对比、差值对比、平均值对比等，对Bonnie飓风做了进一步分析。对比结果一致，印证了TRMM数据的可靠性，同时进一步验证了双束立体雷达算法的联合算法的可靠性。
关键词: Bonnie飓风    机载雷达    TRMM卫星    
A Case Comparison Between the TRMM Data and Airborne Radar Data in Rainfall Retrieval
Chen Tingdi, Wang Lianzhong, Dou Xiankang     
School of Space and Earth Science, University of Science and Technology of China, Hefei 230026
Abstract: Precipitation radar (PR) on the Tropical Rainfall Measuring Mission (TRMM) is the first spaceborne instrument capable of producing three dimensional structure of rainfall. Information about each individual tropical cyclone (TC) can also be provided by airborne radar. Both airborne and spaceborne radars have a lot in common and their observing data are comparable. But it's difficult to get proper cases with good coincidence to perform significant comparison. Only hurricane Bonnie is selected as a study case. On August 26, 1998, a flight is made by NOAA/P3 plane at 11:30 along the east coast of America, and a close observation on hurricane Bonnie is made by the dual beam airborne radar placed on it. Almost at the same time the TC core is fully observed by TRMM orbits. Before comparing with TRMM, P3 radar data need to be processed. The measured reflectivity factor (Z-field) of P3 radar is corrected for path attenuation using the hybrid dual beam/stereoradar algorithm. The absolute error in the radar calibration is also corrected. The typical sampling time of a hurricane by the airborne P3 radar is about one hour, while it is one or two minutes for the TRMM PR. Therefore, the nearly instantaneous rain pattern observed by the PR may evolve and move during the airborne radar sampling. Such an effect is reduced by restricting the region for comparisons to a domain where the maximum time lag between the two samplings do not exceeding 600 s. Also, the rain pattern is corrected for advection using a model of horizontal tangential speed (Vt) of individual rain cell versus the radial distance to the eye center. Considering different cross range resolution, TRMM is interpolated on the P3 grid. Then a serial of comparisons is made between P3 and TRMM data. Comparisons of vertical cross section of TRMM and P3 corrected reflectivities are given, and the data agree with each other well within the comparison domain. Outside this area, a large part of the hurricane where the time lag between the two samplings exceeds 600 s can't be used for significant comparisons. Point to point comparis ons of all rain, stratiform rain and convective rain show that most of the data points are along the diagonal and have a standard deviation of 3.9 dBz. The associated histogram of differences ΔZ is sharply peaked, the mean difference is 0.7 dBz with a standard deviation of 6.1 dBz. The mean vertical rainfall density profiles retrieved from the P3 and TRMM show they agree with each other very well above 5 km and have a little difference within 2—5 km. All the comparison results show that these data are in good agreement. By comparing the data of P3 and TRMM in hurricane Bonnie, the TRMM results a re validated, so is the hybrid algorithm and also the understanding of TC precipitation field is improved.
Key words: Bonnie     airborne radar     TRMM    
引言

雷达作为一种有力的探测手段已被广泛应用, 但20世纪80年代以前使用的雷达主要是地基雷达, 90年代以后机载大气多普勒雷达开始被逐渐使用并显示出诱人的前景[1]。和地基雷达相比, 机载雷达的优势明显:自然界中大气现象如对流系统的形成在地理位置上分布是随机的, 同时雷达观测半径又是有限的, 这样地基雷达只能观测方圆几百公里内的降水, 而机载雷达可以方便地跟踪观测对象, 并且可以观察地基雷达较难观察的区域(如海洋)。由于机载雷达受天线尺寸的限制, 如果要获得一个较好的束向分辨率, 就不得不使用X波段的频率, 而该波段的电磁波穿过雨区时会受到衰减, 因此, 直接利用视反射率进行降水反演会产生很大误差, 而双束-立体雷达算法等算法被证明能够对衰减进行很好的修正[2-6]。

近年来全球气候变化现象引起人们的重视, 如全球变暖、厄尔尼诺等。这些变化的一个重要原因是水及水汽的循环问题。解决这些问题需要对热带水域进行大范围长时间的连续观测, 机载雷达在这些方面也显得无能为力。美国NASA和日本NASDA联合开发了TRMM卫星, 于1997年11月28日发射成功, 该卫星旨在测量热带和亚热带的降水、能量交换及热带降水对全球气候的影响[7-9], 其上搭载的第一部星载降水雷达PR(precipitation radar)[10]首次实现了从太空探测降水三维空间分布。过去进行数据对比研究大多是利用TRMM PR数据与地基雷达数据对比, 然而TRMM覆盖范围很广, 地基雷达却受到地理位置和覆盖范围的限制, 对于海洋地区或特定事件的观测对比就不能够实现。机载雷达则能够弥补这种不足。TRMM PR与机载雷达观测有一定的相似处, 比如两者都从空中向下垂直观测, 观测范围都较大; 雷达所用的波长都很短, 对衰减敏感, 要在算法上做出订正[11-13]; 水平视场大, 要考虑束内填充效应[14-15]。正是由于这些相似之处, 为机载雷达与TRMM PR的观测数据对比提供了可能。通过对同一事件采用不同观测手段获得结果的对比, 不但可以对该事件有一个更加全面的了解, 而且观测结果的对比同样可以印证观测手段的可靠性, 或发现问题。另外当机载或星载雷达的反演算法有所改变时, 通过不同测量方法之间的对比也同样可以看出新算法的优劣, 提高反演精度。

1 TRMM数据和机载雷达数据简介

Bonnie(1998年8月19-30日)是直接横扫北卡罗莱纳州海岸的3级飓风, 但是它造成的损失仅类似于2级飓风Bertha, 这得益于对它进行了足够的观测和相对以前更加准确的预报。在它的形成发展过程中, 采用了多种观测手段, 其中包括NOAA的WP-3D, G-IVSP以及NASA的DC-8飞机等进行了多次观测飞行, 积累了丰富的观测资料。1998年8月26日, 一架WP-3D(N42RF)在11:30(世界时, 下同)到达Bonnie飓风所在地并开始了观测, 与此同时TRMM卫星也几乎在同一时刻扫过该区域, 这两组数据为机载、星载雷达测量数据在降雨反演中的对比提供了条件。

1.1 TRMM数据

TRMM PR的工作频率为13.8 GHz, 波长2.2 cm, 3 dB波束宽0.71°, 扫描角度空间范围为±17°, 星下点水平分辨率4.3 km, 刈幅宽度215 km, 每条扫描线由49个像素(即角库)组成。文中利用的TRMM数据为NASA提供的二级产品中2A25数据, 是经过衰减订正和非均匀分布修正后的数据, 网格距约为4 km×4 km×0.25 km, 包括逐条轨道上的降水率、反射率因子、雨滴谱参数、Z-R关系式中参数和降水类型[16-17]等信息。2A25数据中将18 dBz视为噪声域值, 而略去小于18 dBz的资料。本文中采用的是8月26日TRMM 2A25数据(#4283)给出的反射率因子。

1.2 机载雷达资料

本文使用的飞机数据为NOAA的WP-3D飞机尾部雷达所测数据。飞机飞行高度为7.6 km, 低空(小于4.8 km)时可飞行8.5 h, 4100 km, 高空时可飞行10.5 h, 6100 km。雷达工作频率为9.315 GHz, 工作波长为3.22 cm。这里采用的是飞机于8月26日11:36:00至12:19:00期间所探测到的数据。该数据记录在数字式录音磁带上, 是沿雷达波束探测方向上记录的, 主要记录视反射率, 探测的倾角、仰角, 时间, 经纬度, Z-R关系参数等信息。

由于飞机记录的数据并非网格点数据, 所以必须对数据进行一系列处理。首先将其插值到1.5 km×1.5 km×0.4 km的网格上, 形成可用算法进行反演的规范数据。反演算法用的是双束算法[18]-立体雷达算法[19]的联合算法。这种联合算法避免了双束算法反演中在雨团中心雨强大处的不稳定性、立体雷达算法对于边界的要求非常苛刻的缺点, 充分发挥了两种算法的优越性, 更具适用性和准确性[20]。

由于飞机以约120 m/s的速度飞行, 对于飓风, 机载雷达的典型取样时间约为1 h左右, 而TRMM卫星扫描相同的区域只要1~2 min。因此, 与卫星相比, 飞机测量的时间段里雨场会有明显的发展变化。为了使得卫星数据和飞机数据具有可比性, 通过限定对比区域, 缩短对比数据的时间差来实现。由于雨场在一个相对较短的时间(本文中延时取600 s)里变化不会很大, 可近似认为卫星与飞机所测量的雨场相同, 保证了数据的可对比性; 考虑到观测系统的平移与旋转, 引入一个水平切线速度Vt(单位:m/s):

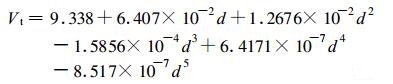
(1)

式(1)中, d为测量点到飓风中心的距离, 利用上式可推算出测量点在卫星扫描时所在的位置, 即用飞机在较短时间内的测值, 推算出飞机探测开始时的瞬时雨场。

2 TRMM数据与机载雷达数据对比分析

对比数据选择以32.2°N, 78.4°W为坐标原点, 对飞机反演的数据与TRMM数据作对比分析。

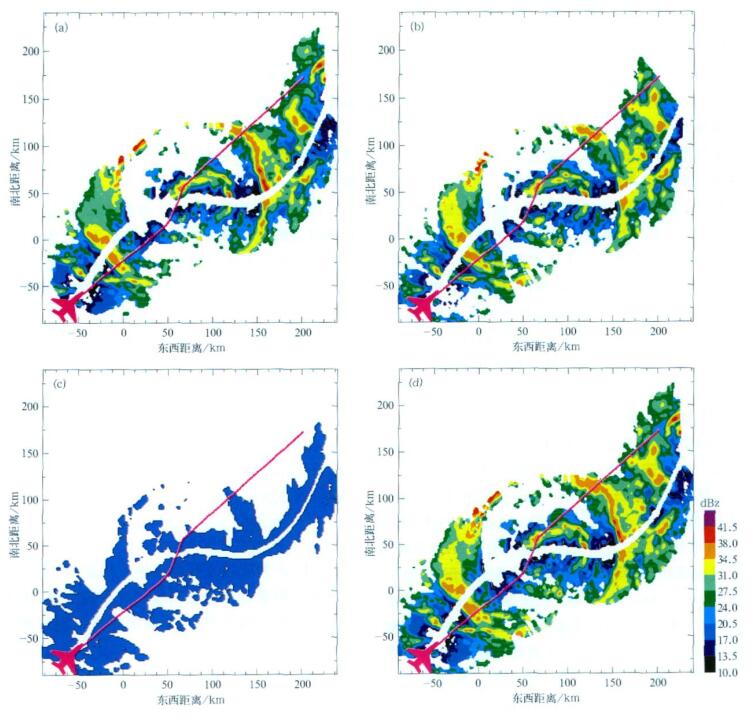
2.1 平面图对比

绘画中的网格为221×221× 34, 格距为1.5 km×1.5 km×0.4 km, 图 1给出P3飞机在2.1 km高度上数据, 这部分数据经过插值并且已经考虑Vt作用, 图中实线代表飞机实际飞行的路线。图 1c中的区域是这样确定的, 这一区域中前向和后向的PIA(path-integ rated attenuation)因子中至少有一个是可以忽略的[19], 这个区域是双束-立体雷达算法的联合算法反演时所必须的。

图 1. P3飞机所测的2.1 km高度上Bonnie飓风的视反射率因子分布 (a)前向视反射率因子,(b)后向视反射率因子,(c)边界条件,(d)最大视反射率因子 Fig 1. Reflectivity factors measured by P3 radar in Bonnie at 2.1 km height (a)foreward reflectivity,(b)backward reflectivity,(c)boundary condition,(d)maximum reflectivity factors

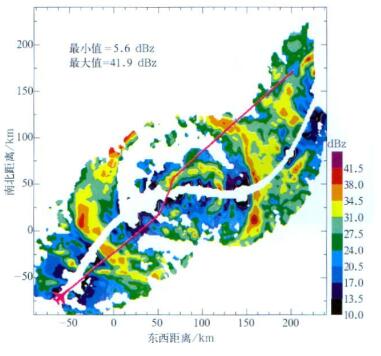
图 2是利用双束-立体雷达的联合算法反演后得到的2.1 km高度上Bonnie飓风的反射率因子分布情况。图中实线为飞机的实际飞行路线和考虑Vt作用后的测值分布情况。可以看出飞机飞行一段时间后测到的是离飞行路线较远区域的值, 由于时间相差较多, 其值变化也较大。

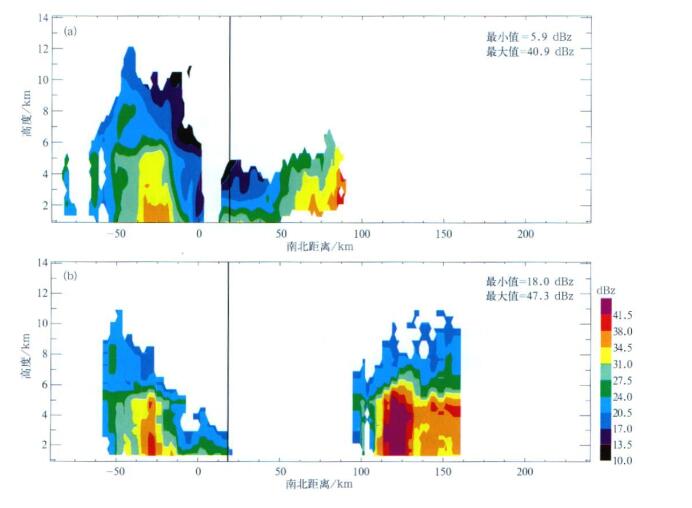
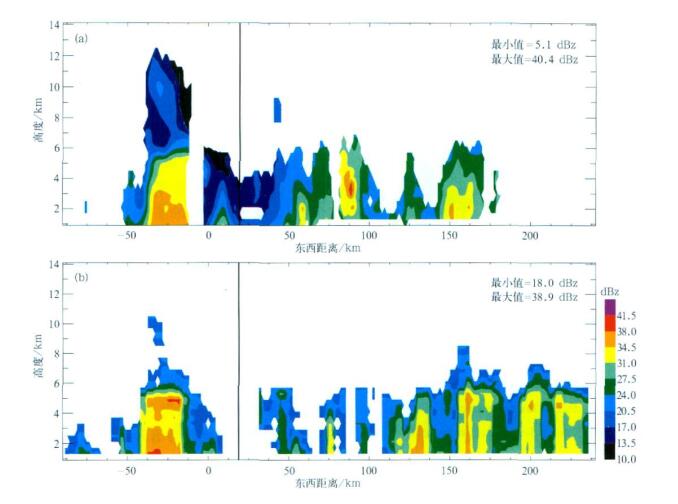
2.2 切面图对比

虽然用Vt可以使测点位置还原, 但随时间变化而变化的雨场值却无法还原。数据对比中发现, 在较短(本文中取600 s)的时间内, 雨场反射率因子变化不大。对图 2沿x=0(即沿78.4°W经线)和y=0(即沿32.2°N纬线)两个方向取两个切面, 与相同位置TRMM垂直切面上的反射率因子数据进行对比, 分别为图 3和图 4。如前面提到的对比时间延迟和飞机的飞行速度的关系, 能较好进行对比的区域不超过75 km为宜, 飞机计时开始位置距图 3和图 4中的竖线位置约75 km。从图 3中可以看出, P3的反射率因子最大值和最小值分别为40.9 dBz和5.9 dBz, 而TRMM的反射率因子最大值和最小值分别为47.3 dBz和18 dBz。在竖线的左面, 即选定的比较范围内, P3和TRMM数据反射率因子的大小和位置都对应的较好; 而竖线的右边飞机探测的范围没有卫星探测的范围大。即使两者都有测值的区域, 反射率因子也相差很多。这是因为两组数据在测得时间上差距较大, 测点的强度已经有了很大改变, 所以该区域不属于比较范围。TRMM的最大值正是出现在竖线的右边, 不在选定的对比区域中。最小值之间的差异主要是由于TRMM将18 dBz作为其噪音阈值, 所以飞机数据中很多地方出现10~18 dBz值区, 对应的在TRMM数据中则为零值区。图 4中给出的是沿y=0方向的切面, 与图 3类似, 在竖线的左边, P3和TRMM数据反射率因子的大小和位置也有较好的对应。图 3和图 4的对比中, 由于是将TRMM的数据按飞机数据网格点进行了插值, 而TRMM数据的水平网格距约为飞机数据水平网格距的3倍, 所以在插值时, TRMM的图中很多地方表现出的是平均值特征。

图 2. 利用双束-立体雷达的联合算法反演P3飞机数据得到的2.1 km高度上Bonnie飓风反射率因子 Fig 2. Reflectivity factors of Bonnie corrected by hybrid algorithm using P3 radar data at 2.1 km height

图 3. Bonnie飓风经向切面反射率因子图(x=0) (a)P3飞机,(b)TRMM Fig 3. Meridional cross-section (x=0) of reflectivity factors in Bonnie (a)P3,(b)TRMM

图 4. Bonnie飓风纬向切面反射率因子图(y=0) (a)P3飞机,(b)TRMM Fig 4. Zonal cross-section(y=0)of reflectivity factors in Bonnie (a)P3,(b)TRMM

在两图限定对比区域内, 数据都对应很好, 本文对比中所用到的数据也都取在这个限定区域内, 即测点时间差小于600 s。

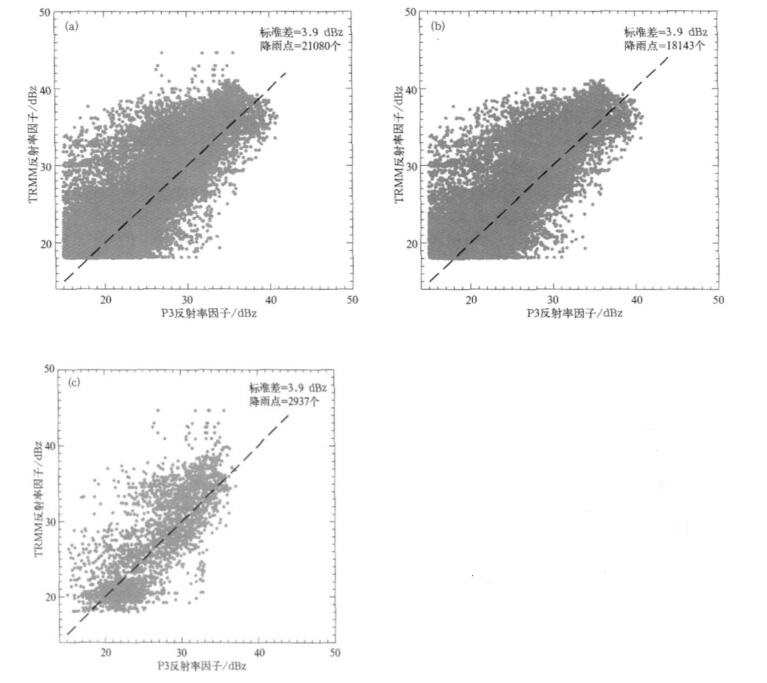
2.3 散点图对比

在对比区内根据降水类型做点对点的比较。TRMM卫星的2A25还提供了降水类型的数据信息, 依据0 ℃层是否出现亮带, 以及回波中信号强度(一般超过39 dBz为对流性降水)等来定义降水类型[21]为层状云降水、对流性降水和其他类型降水; 对飞机所测的数据也做了简单的降水类型分类:在3 km的高度层上, 将反射率因子小于37 dBz的点定义为层状云降水, 反射率因子大于37 dBz的点定义为对流性降水。图 5分别按全部降水、层状云降水、对流性降水给出点点对应的比较。

图 5. 飞机测量反演反射率因子与TRMM反射率因子点对点对比 (a)全部降水,(b)层状云降水, (c)对流性降水 Fig 5. Comparisons between reflectivity factors retrieved by P3 and TRMM (a)all rainfall,(b)stratiform rainfall, (c)convective rainfall

从图 5中易知, 对比区内定义的层状云降水点占全部降水的主要部分; 点的分布虽然基本上是以y=x的直线对称分布的, 但相对离散, 标准差达到3.9 dBz。这可能是由于对机载数据反演中对于降水类型的划分较TRMM PR的简单, 使整个空间上存在降水类型与实际不相符合的情况。

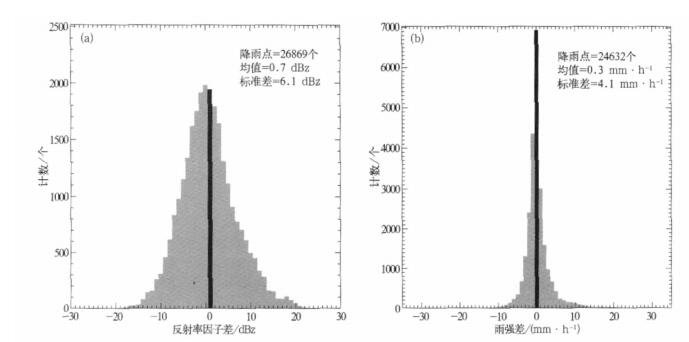
2.4 差值对比

图 5只能反映点的分布, 却不能获知距y=x线近的点的数目, 数目多则说明飞机数据与TRMM卫星数据对应关系较好, 反之对应不好, 而图 6正好可以反映这一情况。如图 6所示, 图 6a、图 6b分别为TRMM与P3的点对点反射率因子之差和雨强之差。图 6a的反射率因子差以0为中心对称分布, 大部分的点都集中在0值附近, 也有偏差较大的, 但这些点的数量相对总的对比点数量是极小的一部分, 图 6b的雨强差中也可得到同样的规律, 说明飞机数据与TRMM卫星数据有较好的对应关系。反射率因子差平均值为0.7 dBz, 雨强差平均值为0.3 mm·h-1, 都是TRMM的值大一些, 这可能是由于在将TRMM数据插值到飞机网格点上时, 这些插值相当于是TRMM数据的平均值, 总体上会使TRMM数据值偏大。

图 6. 飞机测量与TRMM差值统计 (a)反射率因子,(b)降水 Fig 6. Histogram of the differences between P3 and TRMM (a)reflectivity factor,(b)rainfall

2.5 平均值对比

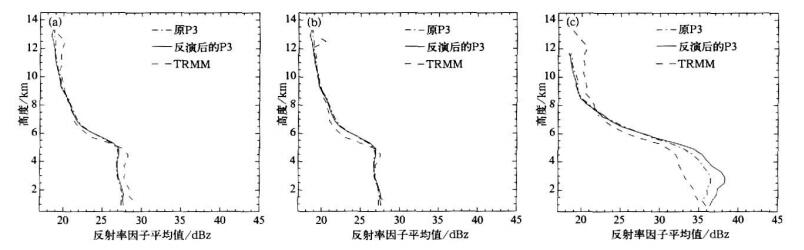
图 7分别给出全部降水、层状云降水、对流性降水反射率因子平均值沿高度的分布图。从图 7a中可以看出P3和TRMM的全部降水反射率因子平均值在5 km以上虽互有大小变化, 但是其值十分接近, 且都随着高度的增加而迅速减少。在5 km以下, TRMM值总体比P3值大1 dBz左右, 估计主要是由于探测手段不同引起的。TRMM PR的波束达到这一高度时已经变得比较宽, 其水平分辨率较低, 它的平滑作用给降水系统的结构、回波面积和降水的探测都带来比较大的影响。同时飞机在这一区域中波束宽虽然比PR的情况好, 同样由于衰减效应, 其值较真值也会产生偏离, 从而导致了在此高度范围内TRMM与P3的差异。由于层状云降水占全部降水的绝大多数, 所以图 7b中P3和TRMM层状云降水反射率因子与图 7a中P3和TRMM全部降水反射率因子变化趋势类似, 且P3和TRMM反射率符合得更好。图 7c中P3的对流性降水反射率因子平均值3 km以上基本随高度的增加而减少, 在3 km左右出现极大值, TRMM则没有类似的极值出现, 且P3反射率因子在高度较低时大于TRMM数据。但是由于该类降水很少, 对全部降水的反射率因子并没有太大的影响。

图 7. 反射率因子平均值分布曲线图 (a)全部降水,(b)层状云降水,(c)对流性降水 Fig 7. Mean reflectivity factor profiles (a)all rainfall,(b)stratiform rainfall,(c)convective rainfall

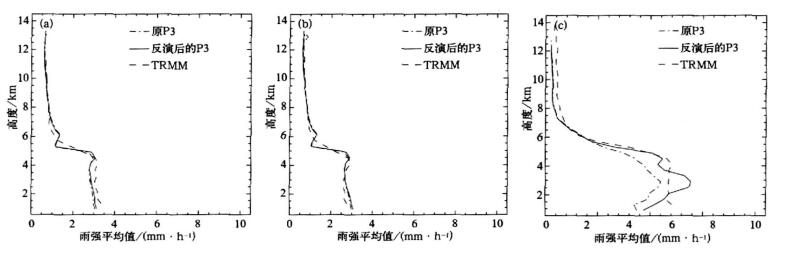
图 8给出了反演得到的雨强平均值沿高度分布图。从图 8a和图 8b中可以看到, P3和TRMM降水平均值曲线符合得很好, 且与图 7a和b中反射率因子平均值的变化趋势相对应。图 7c和图 8c是对流性降水的Z与R的平均值。在图 7c中, 5 km以下TRMM值远小于P3的值, 图 8c的对流性降水平均值图中, TRMM值却与飞机测量值差不多。这主要是由于对于降水分类的方法不同、对比时将TRMM数据插值到飞机网格上以及对强降水反演修正的方法不同造成的。不过从前面的分析中已知, 这类降水点在所取区域中很少, 这一部分对全部降水的平均值的影响不大。

图 8. 雨强平均值分布曲线图 (a)全部降水,(b)层状云降水,(c)对流性降水 Fig 8. Mean rainfall density profiles (a)all rainfall,(b)stratiform rainfall,(c)co nvective rainfall

总体来说, 利用双束-立体雷达算法的联合算法反演P3数据后得到的降水平均值曲线图与TRMM数据符合较好, 这也印证了该联合反演算法具有较高的反演精度。

对于高度低于2 km的情况, 由于回波信号受地表的影响较大, 会产生较大误差, 因此不作对比分析。

3 结论

通过P3飞机雷达和TRMM卫星对Bonnie飓风测量数据比较得出:在较短的延迟时间(600 s)内, P3飞机与TRMM所测的结果都是一致的, 特别是层状云降水部分, 反演结果对比中两组资料一致性更高。在5 km以下, 机载、星载雷达波长短、受衰减效应影响大的特点在平均值图中体现得很明显, 使得这部分数据存在着一些小的差异。总的来说, 以上一系列对比充分印证了TRMM卫星测量资料的可靠性。

文中对于机载雷达的测量资料, 采用了双束-立体雷达算法的联合算法[20]。从降雨反演的结果可以看出, 机载雷达数据与TRMM卫星数据一致, 从而印证了这种联合算法具有可靠的反演精度, 适用于机载雷达数据。

参考文献
[1] Hildebrand P H, Moore R K, Meteorological radar observation from mobile platforms. Radar in Meteorology, 1990: 287–314.
[2] Testud J, Amayenc P, Stereoradar meteorology:A promising technique for observation of precipitation from a mobile platform. J Atmos Ocean Technol, 1989, 6: 89–108. DOI:10.1175/1520-0426(1989)006<0089:SMAPTF>2.0.CO;2
[3] Kabeche A, Testud J, Stereoradar meteorology:A unified approach to process data from airborne or ground-based meteorological radars. J Atmos Ocean Technol, 1995, 12: 783–795. DOI:10.1175/1520-0426(1995)012<0783:SMANUA>2.0.CO;2
[4] Oury S, Testud J, Marecal V, Estimate of precipitation from the dual beam airborne radars in TOGA-COARE. Part Ⅰ:The K-Z relationships derived from the stereo-and quad-beam analysis. J APPl Meteor, 1999, 38, (2): 156–174. DOI:10.1175/1520-0450(1999)038<0156:EOPFTD>2.0.CO;2
[5] Testud J, Oury S, Algorithme de correction d'atténuation pour radar météorologique. C R Acad Sc Paris, t324, serieIIa, 1997: 705–710.
[6] Oury S, Dou X K, Testud J, Estimate of precipitation from the dual beam airborne radars in TOGA-COARE. Part Ⅱ:Precipitation efficiency in convective cells, case study of 9th February 1993. J Appl Meteor, 2000, 39, (12): 2371–2384. DOI:10.1175/1520-0450(2000)039<2371:EOPFTD>2.0.CO;2
[7] Simpson J, Adler R F, North G R, A proposed Tropical Rainfall Measuring Mission(TRMM)satellite. Bull Amer Meteor Soc, 1998, 69: 278–295.
[8] Tao W K, Smith E A, Adler R F, et al. Retrieval of latent heating from TRMM measurements. Bull Amer Meteor Soc, 2006, 87, (11): 1555–1572. DOI:10.1175/BAMS-87-11-1555
[9] Tao W K, Simpson J, Sui C H, et al. Retrieval algorithms for estimating the vertical profiles of latent heat release:Their applications for TRMM. J Meteor SocJapan, 1993, 71: 685–700.
[10] Kummerow C, Barnes W, Kozu T, et al. The tropical rainfall measuring mission(TRMM)sensor package. J Atmos Ocean Technol, 1998, 15, (3): 809–817. DOI:10.1175/1520-0426(1998)015<0809:TTRMMT>2.0.CO;2
[11] 窦贤康, 刘万栓, 刘锦丽. 机载雷达定量测雨中衰减效应的订正研究. 大气科学, 1999, 23, (4): 403–410.
[12] 窦贤康, 刘万栓, 刘锦丽. 用机载雷达资料反演雨空间结构. 遥感学报, 1999, 3, (3): 203–208.
[13] 窦贤康, 刘万栓, 胡先鹏. 用TOGA/COARE试验中机载雷达资料进行衰减效应订正的个案研究. 电波科学学报, 1998, 13, (1): 6–10.
[14] Kozu T, Iguchi T, Meneghini R, et al. Preliminary Test Results of a Rain rate Profiling Algorithm for TRMM Precipitation Radar. Proceedings of SPIE on Microwave Remote Sensing of the Atmosphere and Environment Beijing China, 1998: 86–93.
[15] 窦贤康, 刘万拴, Amayenc P, 等. 不均匀性束内充塞效应对星载测雨雷达反演算法的影响. 大气科学, 2000, 24, (4): 568–576.
[16] Kummerow C, Simpson J, Thiele O, et al. The status of the Tropical Rainfall Measuring Mission(TRMM)after two years in orbit. J Appl Meteor, 2000, 39, (12): 1965–1982. DOI:10.1175/1520-0450(2001)040<1965:TSOTTR>2.0.CO;2
[17] Iguchi T, Kozu T, Meneghini R, et al. Raln-profiling algorithm for the TRMM precipitation radar. J Appl Meteor, 2000, 39: 2038–2052. DOI:10.1175/1520-0450(2001)040<2038:RPAFTT>2.0.CO;2
[18] Testud J, Amayenc P, Marzoug M, Rainfall-rate retrieval from a spaceborne radar:Comparison between single-frequency, dualfrequency, and dual-beam techniques. J Atmos Ocean Technol, 1992, 9: 599–623. DOI:10.1175/1520-0426(1992)009<0599:RRRFAS>2.0.CO;2
[19] 窦贤康, TestudJ. 立体雷达方法在星载测与雷达上的. 应用气象科学, 1999, 57, (3): 358–366.
[20] 王连仲, 窦贤康. 机载测雨雷达两种反演方法的优化和综合利用的模拟研究. 大气科学, 2007, 13, (2): 265–272.
[21] Awaka J, Iguchi T, Okamoto K, Early Results on Rain Type Classification by the Tropical Rainfall Measuring Mission(TRMM)Precipitation Radar. Pro 8th URSI Commission F Open Symp, Averior, Portuga, 1998: 134–146.