应用气象学报  2008, 19 (3): 326-332   PDF    
引用本文
史玉光, 孙照渤, 杨青. 新疆区域面雨量分布特征及其变化规律[J]. 应用气象学报, 2008, 19(3): 326-332.
Shi Yuguang, Sun Zhaobo, Yang Qing. Characteristics of Area Precipitation in Xinjiang Region with Its Variations[J]. Journal of Applied Meteorological Science, 2008, 19(3): 326-332  
新疆区域面雨量分布特征及其变化规律
史玉光1,2, 孙照渤1, 杨青3     
1. 南京信息工程大学, 南京 210044;
2. 新疆维吾尔族自治区气象局, 乌鲁木齐 830002;
3. 中国气象局乌鲁木齐沙漠气象研究所, 乌鲁木齐 830002
2007-08-28 收到, 2008-01-18 收到修改稿.
资助项目: 国家自然科学基金项目 (40775056) 和中国气象局气候变化研究专项 (CCSF2008-8) 共同资助    
摘要: 将自然正交分解 (EOF) 和数字高程模型 (DEM) 相结合, 利用新疆区域144个气象站和水文站的1961—2005年降水量资料, 计算得到新疆区域面雨量年、季分布特征和变化规律。分析结果表明:新疆区域年平均面雨量约为2724.6×108t, 年平均降水量为165.5 mm。从空间分布来看, 天山山区面雨量最大, 约占全疆面雨量的40.4%, 该区域年平均降水量为409.1 mm; 北疆地区次之占34.3%, 年降水量为277.3 mm; 南疆地区最少约为25.3%, 年平均降水量仅有66.2 mm。从季节分布来看:夏季面雨量最大, 约占全年面雨量的54.4%;春季次之为23.6%;秋季为16.5 %; 冬季最少, 约为5.5%。新疆区域面雨量年际变化呈现出增多的趋势, 1987年存在突变, 在此之后降水量明显增多。
关键词: 新疆    面雨量    气候变化    
Characteristics of Area Precipitation in Xinjiang Region with Its Variations
Shi Yuguang1,2, Sun Zhaobo1, Yang Qing3     
1. Nanjing University of Information Science & Technology, Nanjing 210044;
2. Xinjiang Meteorological Bureau, Urumqi 830002;
3. Institute of Desert Meteorology, China Meteorological Administration, Urumqi 830002
Abstract: Using the data of precipitation including 144 meteorological and hydrological stations in Xinjiang from 1961 to 2005, annual and seasonal distributing features and its variations of area precipitation in Xinjiang are discussed by empirical orthogonal function (EOF), multiple regression analysis, maximum entropy analysis and so on, combining with 1 km×1 km gridding data of digital elevation model (DEM). Results show that mean annual area precipitation in Xinjiang region is 2724.6×108t and mean annual precipitation is 165.5 mm. For space distribution, area precipitation of Tianshan Mountains, Northern Xinjiang and Southern Xinjiang respectively occupy about 40.4%, 34.3% and 25.3% of all regions, and its mean annual precipitation are 409.1 mm, 277.3 mm and 66.2 mm, respectively. Area precipitation in summer is the most one about 54.4% of all year, 23.6% in spring, 16.5% in autumn, and the least 5.5% in winter. In the last 45 years area precipitation in Xinjiang presents clear annual variations and increasing trend, especially since 1987.
Key words: Xinjiang region     area precipitation     climate change    
引言

新疆位于我国西北部, 东西最长达1900 km, 南北最宽为1500 km, 面积约164 ×104 km2, 约占我国陆地面积的六分之一。新疆地处欧亚大陆腹地, 四面高山环抱, 地理特征独特, 生态环境脆弱, 水资源分布极不均匀, 是典型的干旱、半干旱地区。降水是新疆所有形式的地表水、地下水和高山积雪冰川等水体的根本补给源, 是水分循环过程中的一个重要分量。降水不仅决定着新疆水资源总量, 而且它的空间分布和随时间的变化直接影响着新疆的水分布状况、河川径流形成等, 直接关系到新疆的生态环境与经济社会的发展, 实际工作中更需要了解区域的总降水量的分布特征及其变化规律。

面雨量是一个区域的降水量总和, 能客观地描述该区域实际降水资源状况。面雨量的多少对一个区域的河水径流量影响很大, 是水分循环、气候-水文模式研究中一个重要的基础数据, 也是洪水预报中非常重要的指标之一, 它是气象与水文相互结合的桥梁和纽带。我国在“八五”期间, 开展了致洪暴雨预报方法的研究, 对面雨量的计算方法进行了大量研究, 并在七大江河流域进行了广泛应用[1-9]。

新疆在面雨量方面的研究还处于探索阶段。由于新疆地形复杂, 台站稀少分布不均, 尤其在降水集中的山区更为稀少, 以往的一些研究大多是采用台站数据进行简单的算术平均来代表新疆区域的平均降水量, 随着观测资料的积累, 计算能力的提高, 精细化地计算新疆面雨量是一项十分重要的工作。

面雨量计算方法有多种, 主要采用实况插值法、要素回归法、遥感相关法、神经网络法、物理模型法等[10-18], 这些方法有各自的适用条件。本文将以DEM (digital elevation model) 为基础, 结合自然正交分解 (EOF)、多元回归等方法, 建立插值模型, 计算新疆区域不同季节、不同区域的面雨量序列, 研究其时空分布特征及变化规律。

1 资料与方法 1.1 资料与区域的划分

利用1961—2005年新疆境内144个气象站和水文站观测的降水量资料, 结合DEM数据GTOPO30 (global digital elevation model), 使用水平空间分辨率为30″, 近似1 km×1 km的网格资料, 对新疆区域面雨量进行计算。

根据影响新疆降水的天气气候特点和地理要素把新疆分为3个特征明显的区域:北疆、南疆、天山山区 (海拔高度≥1500 m, 含伊犁河谷)。本文基于地理信息精细化计算各区域面雨量时, 首先确定天山山区的边界, 通过实验分析, 在天山附近选取海拔高度≥1500 m的区域确定为天山山区。考虑到伊犁河谷地处天山之中, 气候特征相近, 虽然有部分地区海拔高度 < 1500 m, 但仍将其划入天山山区。在天山与昆仑山交接处以直线分割, 在天山最东段也以直线分割。因此本文所指的北疆、天山山区、南疆的范围在细节上可能与过去的区域定性描述有一点差异。本文所计算出的新疆区域总面积为164×104 km2, 其中北疆区域面积为33.65×104 km2, 天山山区面积为27.08×104 km2, 南疆区域面积为103.27×104 km2。

1.2 插值计算方法

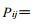
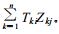
根据新疆区域降水的变化规律和特点, 本研究首先运用经验正交分解 (EOF) 对新疆区域各站历年降水量矩阵P(45×144) 进行分解, 将其分解为n个空间函数Z和时间函数T乘积的线性组合:一般情况下, 原始场的主要信息仅用前几个特征向量和时间系数就能得到充分的反映。

由此可知, 每个特征向量都有n个分量组成, 与n个站点相对应, 即每个分量对应一组经纬度和高度值。

其次, 分别建立前H个特征向量的各分量与地理信息系统中某点位置 (X, Y) 及海拔高度的多元回归方程:

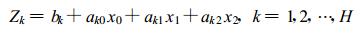
(1)

式 (1) 中, Zk代表回归对象, 即指降水量场的第k个特征向量的分量值; x0, x1, x2分别为X, Y以及海拔高度; bk为第k个特征向量的回归方程常数项。

再以DEM数据为基础, 采用梯度距离平方反比法 (GIDS) 作为插值公式[17], 计算区域内每个网格点l的第k个特征向量值Zkl :

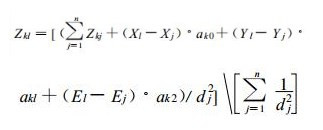
(2)

式 (2) 中, Xl, Xj为待估点l与气象站点j的x轴坐标值, Yl, Yj为待估点l与气象站点j的y轴坐标值, El, Ej为待估点l与气象站点j的海拔高度; dj为待估点l与第j个气象站点的大圆距离; ak0, ak1, ak2是第k个特征向量的各分量与X, Y及海拔高度回归系数, 由式 (1) 求出。选定的参考点为32°N, 72°E, 以求出气象站点和各计算点的坐标值。

最后, 再利用式 (3) 乘以相应的时间系数Tkl并求和:

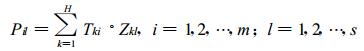
(3)

式 (3) 中, m为序列长度, s为计算区域内网格点总数。回归方程的个数H远小于序列长度m。

由此得到第i年整个新疆区域网格点l的年降水量值Pil, 再乘以相应的面积Bl, 得出该格点的面雨量, 然后再对所有格点的面雨量求和:

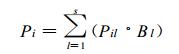
(4)

得出第i年新疆区域的面雨量Pi, 依次指定年份, 重复式 (3) 与 (4) 的计算, 即求出整个流域面雨量序列。

本计算方案结合地理信息系统数据考虑了海拔高度的影响, 也结合自然正交分解 (EOF), 以最少的插值方程给出了要素区域平均的序列值。

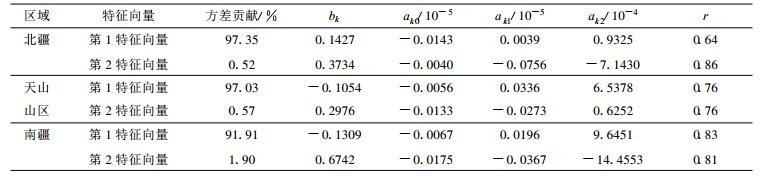
2 结果分析 2.1 EOF及回归方程

对北疆地区47站、天山山区79站和南疆地区58站1961—2005的年降水量场进行EOF分解, 结果表明:年降水量的第1特征向量分别占总方差的97.35%, 97.03%和91.91%, 说明此种分布类型代表了该地区降水量场变化的主要特征, 反映了各区域大气候背景下的一致性; 第2特征向量分别占总方差的0.52%, 0.57%和1.90%, 收敛速度很快, 浓缩了原始场的主要空间分布信息 (表 1)。由此可以看出, 前2个特征向量已完全能够代表原始场时空分布的主要特征。因此, 分别求出前2个特征向量与X, Y及海拔高度因子的回归方程, 其变量系数与式 (1) 对应, r为复相关系数。对回归效果的计算分析表明, 在显著性α=0.05的情况下, 均通过F检验。考虑到建立模型的需要, 并使气候要素在边界过度更连续、合理, 各区域选用的站点也包括了在区域边界外附近的部分站点, 也就是说各区域建模使用的站点在边界附近有一定的重复。

表 1 特征向量与地理因子的回归方程系数 Table 1 Regress equation coefficients between the characteristic vectors and geography factors

2.2 拟合误差分析

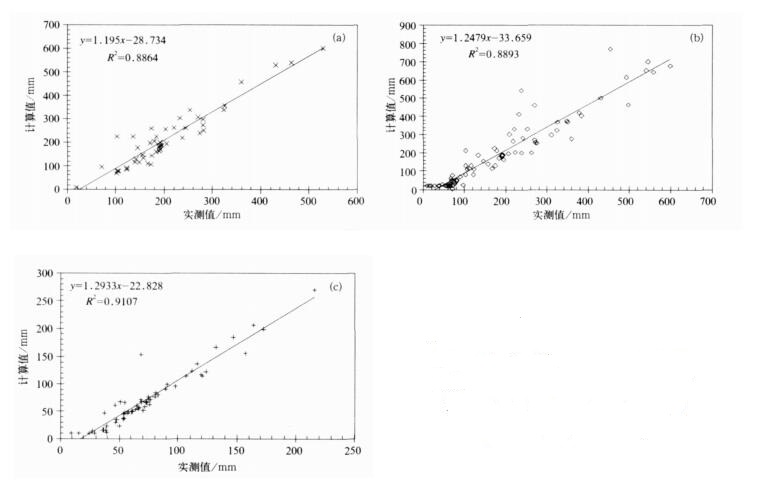
为了检验拟合误差, 分别对各区域建模所用站点的年降水量数据的计算值与实测值分别进行对比 (图 1)。计算结果表明, 各区域站点的计算值与实测值呈现比较好的线性关系, 两者的相关系数分别为0.94, 0.95和0.94。各站点45年平均差异更小, 北疆地区、天山山区和南疆地区的计算值与实测值相对误差分别5.3%, 6.8%和1.2%, 表明本文计算方法可行。

图 1. 计算年降水量与实测值比较 (a) 北疆地区, (b) 天山山区, (c) 南疆地区 Fig 1. Compare between calculating and observing annual precipitation in Northern Xinjiang (a), Tianshan Mountains (b) and Southern Xinjiang (c)

2.3 面雨量特征分析 2.3.1 全区域面雨量分布

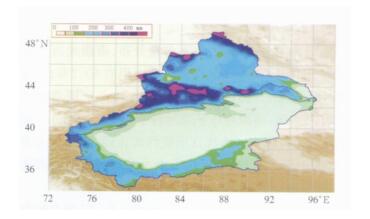
运用式 (1), (2) 和 (3) 进行计算, 即得出新疆区域各网格点的逐年降水量。计算出的新疆区域年降水量的空间分布见图 2。由图 2可见, 降水量基本上呈现北多南少, 西多东少, 山区多平原少的特征, 降水量的大小与地形分布有着十分密切的关系。降水量高值区位于天山山区中西段、阿勒泰山区和塔城的塔尔巴哈台山地区, 降水量在400 mm以上; 降水量低值区大多位于南疆塔里木盆地及哈密南部地区, 降水量低于50 mm; 在哈密北部淖毛湖地区和北疆西部艾比湖地区附近降水量在50~100 mm之间, 200 mm以上的降水大多都集中在山区, 山区降水是新疆区域河水径流主要的补给来源之一。

图 2. 新疆区域降水量分布 Fig 2. Precipitation distribution in Xinjiang

通过计算得出在新疆164.6×104km2的区域上面雨量多年平均值为2724.6×108t, 年平均降水量为165.5 mm。

为了便于比较, 本文还分别用了5 km×5 km, 10 km×10 km, 20 km×20 km, 50 km×50 km等4个不同水平分辨率的网格分别进行计算, 计算见表 2。

表 2 不同分辨率的面雨量 Table 2 The results of area precipitation in different resolution in Xinjiang region

2.3.2 各区域面雨量分布

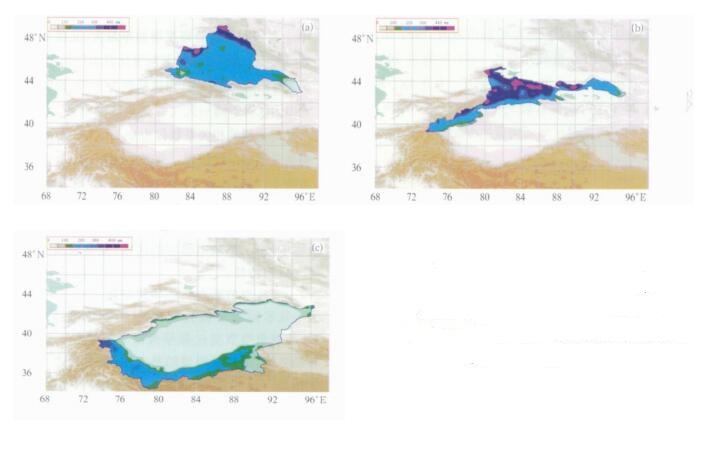
北疆地区面积约为33.68×104km2, 占全疆总面积的20.5% (图 3a); 北疆地区面雨量平均值为934 ×108t, 约占全疆总面雨量的34.3%, 北疆地区平均年降水量为277.3 mm。从图 3a可以看出, 北疆地区的最大降水区在阿勒泰山和塔城北部的塔尔巴哈台山区, 降水量大多在400 mm以上; 准噶尔盆地是降水的低值区, 最小区在北疆西部的艾比湖和东部的淖毛湖地区, 降水量约为50 mm左右。

图 3. 北疆地区 (a)、天山山区 (b) 和南疆地区 (c) 年平均降水量分布 Fig 3. Annual precipitation distribution in Northern Xinjiang (a), Tianshan Mountains (b) and Southern Xinjiang (c)

图 3b为天山山区的降水量分布, 天山山区面积约为26.9×104 km2, 占全疆总面积的16.3%。天山山区面雨量平均值为1101.5×108t, 约占全疆总面雨量的40.4%, 天山山区平均年降水量为409.1 mm, 是新疆地表径流形成的主要源区。此外, 天山山区的最大降水区在天山中部的北坡一带及伊犁河谷两侧, 降水量大多在450 mm以上; 最小区在东天山和天山西南端的南坡附近, 降水量一般为150 mm左右, 这与过去人们的研究和认识是一致的。

图 3c为南疆地区的降水量分布, 南疆地区面积约为104.01×104km2, 占全疆总面积的63.2%;南疆地区面雨量平均值为689.1×108t, 约占全疆总面雨量的25.3%, 南疆地区平均年降水量为66.2 mm。南疆地区最大降水区出现在南疆西部山区, 降水量大多在300 mm左右; 最小区在塔里木盆地和哈密南部地区, 降水量一般为50 mm左右。

上述分析表明, 天山山区面积虽小, 但所占的面雨量最大, 说明山区是新疆的主要水源区; 南疆地区面积大, 分别是北疆和天山山区的3到4倍, 但面雨量却明显的少于北疆和天山山区, 是新疆最干旱的区域。

2.3.3 各季节面雨量分布

新疆面雨量的季节分布存在很大差异。夏季最大, 为1481.5×108t, 占到整个年面雨量的54.4%, 平均降水量为90 mm, 说明夏季是新疆全年降水最多的季节; 春季次之为642.9 ×108t, 占23. 6 %, 平均降水量为39.1 mm; 秋季为449.8×108t, 占16.5%, 平均降水量为27.3 mm; 冬季最少, 面雨量仅有150.4 ×108t, 仅占全年面雨量的5.5%, 冬季降水量平均只有9.1 mm, 是新疆降水最少的季节。

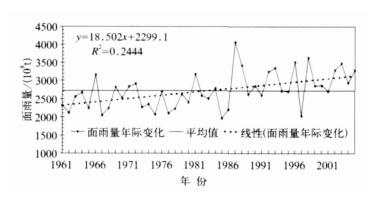
2.4 面雨量变化特征 2.4.1 全区域面雨量变化

图 4为1961—2005年新疆区域面雨量的年际变化曲线, 面雨量最大年份出现在1987年, 高达4060.6×108t, 最低年份为1985年约为1963.6×108t, 相差约2.1倍, 变差系数Cv为0.18。取显著性α=0.01, 相关系数rα=0.38, r实=0.49, |r实|≥rα, 说明新疆区域面雨量的增加趋势在0.01显著性水平上是显著的, 其线性趋势变化率为185×108m3/10a。

图 4. 1961—2005年新疆区域面雨量的年际变化 Fig 4. Annual variation of Xinjiang area precipitation from 1961 to 2005

2.4.2 各区域面雨量变化

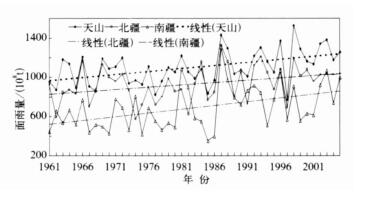
从各区域面雨量的变化特征来看 (图 5), 北疆、天山山区、南疆都不同程度存在上升趋势, 取显著性α=0.01, 相关系数rα=0.38, 天山山区r实=0.47, 南疆区域r实=0.45, 表明|r实|≥rα, 说明天山山区和南疆区域面雨量在0.01显著性水平上增加趋势是显著的; 北疆区域取显著性α=0.05, 相关系数rα=0.30, r实=0.36, |r实|≥rα, 说明北疆区域面雨量的增加趋势在0.05显著性水平上是显著的。

图 5. 不同区域面雨量的年际变化 Fig 5. Annual variation of area precipitation of different regions from 1961 to 2005 in Xinjiang

北疆、天山山区、南疆线性趋势变化率分别为47.6 ×108m3/10a, 61.8×108m3/10a, 75.5×108 m3/10a。其中南疆趋势幅度增加率最大, 北疆最小。北疆与天山山区面雨量的年际变化波动位相十分一致, 两者有很高的相关性, 相关系数为0.78, 说明北疆与天山山区属于同一天气气候系统影响区, 而南疆面雨量与北疆的相关系数仅为0.39, 反映出南疆与北疆属于不同的气候带。北疆、天山山区、南疆的变差系数Cv分别为0.19, 0.16, 0.32, 说明天山山区面雨量年际变化最小; 其次是北疆; 南疆面雨量年际变化幅度最大, 是最不稳定的区域, 充分表现出了干旱区的典型特征。

2.4.3 各季节面雨量的年代变化

从不同季节面雨量的年代变化可以看出 (表 3), 面雨量季节变化都呈现出增长趋势。从降水增幅趋势看, 增长最明显的是冬季, 夏季次之; 春、秋两季相当。20世纪80年代中后期至今降水呈现出明显偏多的趋势, 1986—2005年比1961—1985年春、夏、秋、冬各季分别增加17.4%, 22.2%, 17.6%, 44.3%, 这期间年平均面雨量达3020.2×108m3, 比前期 (60, 70年代) 多两成以上 (21.4%), 比45年平均值多10.8%。1987年是一个明显降水偏多的年份, 四季均表现出明显增多的趋势。

表 3 新疆面雨量各季节年代际变化 (单位: 108t) Table 3 Decadal variations of Xinjiang area precipitation (unit:108t)

3 小结与讨论

研究表明:新疆区域年平均面雨量约为2724.6×108t, 年平均降水量为165.5 mm。从空间分布来看, 天山山区面雨量最大, 约占全疆面雨量的40.4%, 该区域年平均降水量为409.1 mm; 北疆地区次之占34.3%, 年降水量为277.3mm; 南疆地区最少约为25.3%, 年平均降水量仅有66.2 mm。从季节分布来看, 夏季面雨量最大, 约占全年面雨量的54.4%, 春季次之为23.6%, 秋季为16.5%, 冬季最少, 约为5.5%。近45年新疆区域面雨量年际变化呈现出增多的趋势, 尤其是1987年以后降水明显增多。

关于新疆面雨量的问题一直是科学工作者关注的, 本研究采用地理信息数据, 通过自然正交分解和回归分析等技术手段, 推算出新疆区域面雨量年际变化序列和各区域、各季节面雨量年际变化序列。虽然在技术方法上还有一些值得推敲、改进之处, 计算精度也有待于提高, 但这些结果均有助于进一步深入认识新疆降水资源分布规律、全球变化的区域响应和水分循环等科学问题。另一方面, 新疆的水汽主要来自于西风带的水汽输送, 这与我国东部季风降水的水汽主要来自于热带[19]不同。因此, 新疆降水增多的原因, 特别是1987年突变的原因值得今后进一步研究。

参考文献
[1] 傅抱璞. 山地气候要素空间分布的模拟. 气象学报, 1988, (3): 319–326.
[2] 彭春华, 郑启松. 荆江致洪与三峡区间暴雨预报. 空军气象学院学报, 1995, 16, (2): 152–159.
[3] 王仁乔, 李武阶. 日本降水预报的客观订正及三峡区间面雨量的估算. 空军气象学院学报, 1996, 17, (2): 175–180.
[4] 秦承平, 居志刚. 清江和长江干支流域面雨量计算方法及其应用. 湖北气象, 1994, (4): 16–18.
[5] 孟遂珍, 彭治班. 流域平均降水量的一种算法∥新一代气象服务体系研究文集 (二). 北京: 气象出版社, 1999: 112-118.
[6] 董官臣, 冶林茂. 面雨量在气象预报中的应用. 气象, 2000, 26, (1): 9–13.
[7] 徐晶, 林建, 姚学祥, 等. 七大江河流域面雨量计算方法及应用. 气象, 2001, 27, (11): 13–16.
[8] 周筱兰, 张礼平, 王仁乔. 应用最优化订正法制作长江上游面雨量预报. 气象, 2003, 29, (3): 31–33.
[9] 毕宝贵, 徐晶, 林建. 面雨量计算方法及其在海河流域的应用. 气象, 2003, 29, (8): 39–42.
[10] 张学文, 张家宝. 新疆气象手册. 北京: 气象出版社, 2006: 215.
[11] 林开平, 孙崇智, 郑凤琴, 等. 丘陵地区面雨量计算方法及应用. 气象, 2003, 29, (10): 8–12.
[12] 杨扬, 戚建国. 数字卫星云图估算面雨量的应用试验. 气象, 1995, 21, (3): 35–39.
[13] 杨扬. 利用地理信息系统软件计算面雨量. 水文, 1997, 6: 24–27.
[14] 林柄干, 张培昌. 天气雷达测定区域降水量方法的改进与比较. 南京气象学院学报, 1997, 20, (3): 334–346.
[15] 熊秋芬, 胡江林, 夏军. 神经网络方法在静止卫星多通道资料估算中的作用. 气象, 2002, 28, (9): 17–21.
[16] 朱会义, 贾邵凤. 降雨信息空间插值的不确定性分析. 地理科学进展, 2004, 23, (2): 34–42.
[17] 白美兰, 沈建国, 郝润全. 地理信息技术在松嫩流域信息查询和面雨量监测中的应用. 干旱区资源与环境, 2005, 19, (30): 51–54.
[18] Hewitson B C, Crane R G, Gridded area-averaged daily precipitation via conditional interpolation. J Climate, 2005, 18, (1): 41–57. DOI:10.1175/JCLI3246.1
[19] Zhang Renhe, Relations of water vapor transports from Indian monsoon with those over East Asia and the summer rainfall in China. Adv Atmos Sci, 2001, 18: 1005–1017.