2. 南京信息工程大学, 南京 210044;
3. 四川省气象信息中心, 成都 610072
2. Nanjing University of Information Science & Technology, Nanjing 210044;
3. Sichuan Meteorological Information Center, Chengdu 610072
气候资料是进行气候变化研究及气候预测的基础。但长期以来, 由于仪器变动、站址迁移、观测手段变化等因素导致了气候资料产生非均一现象。所谓非均一性, 即气候序列的不连续现象, 它被归纳为人为因素对长期气候观测序列的干扰, 往往对气候变化尤其是区域或局地气候变化检测结果带来明显的歪曲。气候资料的均一性问题一直没有得到很好地解决, 尤其在我国, 这方面的工作开展得很不够。国外许多气候学家在这方面做了大量的工作, 取得了很多重要的进展, 有的甚至已经用于气候资料管理部门的业务化实施[1-5]。近年来我国不少研究人员也开始注重这方面的研究[6-9], 并且分别对我国的探空资料、气温、降水资料以及风速资料等进行了一些均一性检验研究, 并对气温数据作了一些均一化订正, 制作了均一化的中国历史气温数据集[10-11]。这对于我国气候资料的均一性分析工作无疑是非常重要的, 但是也应该看到, 很多工作仍只停留于一些方法的研究和探讨, 或者是孤立地对单个 (几个) 数据集进行订正, 这与科研工作对于气候资料的要求还有很大的差距。许多研究仍然基于原始的没有经过均一化的气候观测序列, 导致研究结论中存在着相当多的不确定性甚至歪曲, 这一问题越来越引起人们的重视。因此, 深入研究各种气候资料要素均一性检验方法以及订正方法, 努力探索气候资料均一化业务实施手段, 仍是当前气候学和气候变化研究面临的难点之一。
在我国, 对于气温数据的均一化调整已经取得了一些突破性进展。而对于降水序列的均一性研究, 则仍然停留于一些尝试性的水平, 原因在于: ①降水资料的变率大, 年以下尺度降水概率分布非正态, 空间代表性差于气温; ②降水数据产生非均一性的原因比气温的更加复杂; ③我国降水数据观测站点密度不足, 国内对气候数据均一性研究的重视十分不够, 等等。因此, 本文拟采取一些较为成熟的技术方法, 结合我国气象观测实际和当前数据均一性研究的一些新成果, 来探讨对降水量数据进行均一化的可能性。
1 资料和分析方法本文采用的资料为国家气象信息中心气象资料室收集整理的长江三角洲地区 (包括上海、江苏部分地区) 共36个地面观测站 (均为国家基准及基本气象站, 见图 1) 的1961—2002年逐月降水总量资料, 该资料序列通过了气象资料室的质量检验。选取1961—2002年序列的原因是考虑到1961年以后台站数目较为稳定, 便于获得更多的观测序列来构造检验参考序列, 从而使检验结果更加合理。

|
|
| 图 1. 长江三角洲地区站点分布图 (站号) Fig 1. Stations distribution of the Yangtze Delta (station number) | |
长期以来国际上发展形成的降水资料的均一性检验方法有很多种, 大都是基于最大似然方法。在对降水资料的均一性检验实践中, 标准正态检验方法[12] (SNHT) 和potter方法[13]应用较多, 但二者比较起来, SNHT方法对于不连续点 (尤其是那些幅度较小的不连续点) 的检测更为理想。标准正态均一性检验 (SNHT) 方法是一种利用临近台站作为参考序列来判断时间序列中的非均一性的参数检验方法。它用来检测待检序列和参考序列之间突变或者线性趋势的差异。Hawkins提出了这一方法[14], 被Alexanderson发展并应用于气候序列[12, 15-16], 最后又得到Alexanderson等的进一步完善[17], 成为现在的4个版本的检验方法[18], 4个版本分别针对于单平均值变化、单平均值和标准差变化、双平均值变化和平均值上的趋势变化四种情况。Tuomenvirta等指出[18], 在SNHT方法中备检序列和参考序列还可以是不同的气候要素, 并且也不一定要求是附近台站的序列。因此, 本文拟采用SNHT方法对长江三角洲地区降水资料进行均一性分析。选择我国站网密度较高、地形变化相对简单的长江三角洲地区, 可以基本保证对降水资料检验可信。另外本文还结合其他不需要考虑站网密度的手段[19]对该地区的降水资料进行检验, 看该思路是否可以在一定程度上避免台站密度不够的问题。
为了分析影响我国降水资料的均一性的原因, 本文收集整理了台站历史沿革数据, 作为检验结果的合理性判别和序列订正的参考依据。自1961年以来, 长江三角洲地区气象台站降水观测变化主要包括了以下几个方面:台站的迁移、雨量器放置高度及雨量器防风罩设置 (表略)
2 对年降水量的均一性检验 2.1 参考序列的构造和检验序列的形成建立待检序列 (cadidate) 的参考序列 (reference) 和检验序列 (diffs或ratios) 是气候序列均一性检验与订正的基础和关键。参考序列必须是均一的, 可以代表待检序列所处位置的真实变化的气候序列, 而事先无法知道哪个台站序列是非均一的, 哪个台站序列是均一的, 因此要尽可能多地选择一些台站合成一个尽可能均一的序列作为参考序列。基于上述的局地台站网, 分别将每一个站的年降水量作为检验序列, 其余所有35站 (并参考其他临近地区台站) 作为备选参考台站构造检验参考序列。具体做法是:从每个待检站临近的所有台站中挑选4个与待检站序列相关系数最高的年降水序列所在的台站, 作为待检台站的参考台站, 利用式 (1) 建立参考序列ri, 由于参考序列回避了个别台站的影响, 所以这个参考序列可以近似地认为是相对均一的。

|
(1) |
式 (1) 中, ρj是待检序列和参考站序列Xji的相关系数, Xj是参考台站序列的平均值。构造检验序列有两种方法, 即差值 (differences) 和比值 (ratios) 法。由于降水资料的空间不连续性, 因此在降水量的均一性检验时一般采用比值法 (Yi为待检序列, Y为其均值)。这样, 构造出来的一个序列可以表示为:
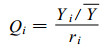
|
(2) |
对该序列进行标准化, 标准化的目的是使得序列的值在1附近波动 (如果是差值则在0附近波动), 并且近似服从N(0, 1) 分布。即:

|
(3) |
SNHT方法目前已经有很多版本, 可以针对不同的要素和实际情况采用不同的版本, 根据降水序列的实际情况, 经过比较, 采用单不连续点平均值检验效果较好。至于两个以上不连续点检验则通过分段来进行检验。
对序列{ Zi} (i=1, 2, ……, n), 假设:
如果{ Zi}序列没有不连续点存在, 则统计假设为:对于任意i, Zi∈N(0, 1)
如果{ Zi}有一个不连续点a, 则统计假设为:

|
(4) |
μ1, μ2分别为假设不连续点a前后两个序列的平均值 (μ1≠μ2), n为样本容量。σ为前后两段的均方差, 因为没有考虑方差间断, 所以前后不变。根据最大似然比率的标准技术[20], 经过一定的近似处理, 构造统计量Ts作为显著性判据:

|
(5) |
Ts的最大值Tmaxs
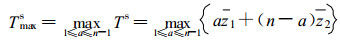
|
(6) |
z1, z2分别表示a前后的平均值, 这样如果Tmaxs大于选定的显著性水平 (临界值与序列长度有关), 解消假设可以被拒绝, 即存在非均一不连续点。表 1给出了0.1及0.05显著性水平下Tmaxs的临界值。
|
|
表 1 0.1, 0.05显著性水平的Tmaxs临界值表 Table 1 The Tmaxs threshold value of 0.05, 0.1 significance levels |
检验过程中面临的一个重要问题是多个不连续点的检验、判断, 这往往需要采取分段检验进行。本文采用的是一种叫半级分段算法进行, 它是针对于全级分段算法而言的, 所谓全级分段算法, 就是我们一般的分段方法, 比如式 (4) 中, 通过二相回归的Tmaxs0.05显著性水平的检验, 被认为是一个突变点T1。判断其他的突变点时, 必须把该序列分为两子段, 即[1, a]和[a+1, n], 再得到两个突变点T2和T3, 依次将子段再分别分为两段, 依次得到T4, T5, ……, 直到子段不能再分为止, 即Nseg<2×Nmin, 一般Nmin取5左右。
上面的分段方法看起来似乎无不妥之处, 但仔细分析, 在T1得出后, 分子段检验得出T2, T3后, T1这个突变点是否成立又成为问题了。如果[T2, T3]之间检验没有得出突变点, 那么下一步的检验将集中在[1, T2], [T2+1, T3], [T3+1, N], 而反之, 如果[T2, T3]之间得到了不同于T1的T′1, 那么下一步的检验则集中在[1, T2], [T2+1, T′1], [T′1+1, T3], [T3+1, N]之间, 依此类推, 直到子段不能再被划分为止 (Nseg<2×Nmin)。显然, 这种半级分段算法比全级分段要优越。
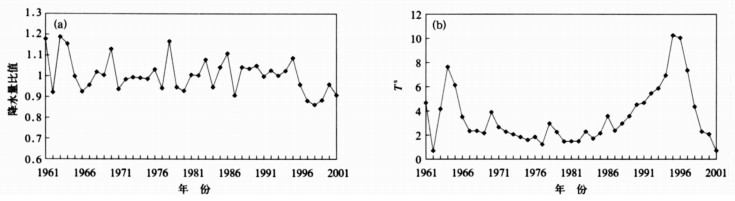
2.3 检验结果用式 (2) 中比值序列 (Ratios) 和式 (5) 中统计量Ts序列来表示检验结果。如前所述, 判别序列是否均一的依据是Ts的极大值, 因此在Ts峰值出现点, 必须做进一步分析和讨论。图 2~4以南京 (58238)、六安 (58311) 和英山 (58402) 3个典型站来说明检验的步骤和结果。

|
|
| 图 2. 南京年降水量比值序列 (a) 和Ts值序列 (b) Fig 2. Annual precipitation ratio series (a) and corresponding Ts series (b) in Nanjing | |

|
|
| 图 3. 六安年降水量比值序列 (a) 和Ts值序列 (b) Fig 3. Annual precipitation ratio series (a) and corresponding Ts series (b) in Liu' an | |
|
|
| 图 4. 英山年降水量比值序列和Ts值序列 Fig 4. Annual precipitation ratio series (a) and corresponding Ts series (b) in Yingshan | |
根据距离和相关性分析, 选定了滁州 (58236)、合肥 (58321)、巢湖 (58326) 及高邮 (58241) 4站作为参考台站, 根据式 (1) 建立年降水量的参考序列, 根据式 (2)~(6), 画出比值序列和Ts值序列 (图 2)。
从图 2a来看, 待检序列和参考序列的比值一直在1附近振荡, 虽然存在许多的峰、谷值, 但都没有达到异常高的情况, 这可以看成是一个均一序列的典型例子; 从图 2b来看, Ts值虽然变化较为明显, 甚至在1998年出现一个最大值3.94, 但比较表 2, 这个值没有达到0.1的显著性水平, 也就是说, 拒绝假设, 即序列是均一的。查看历史沿革变化, 发现从1960年至今, 该站没有发生任何仪器改变、站址迁移和高度变化。因此, 可以得出, 南京站1961—2002年间年降水量序列是连续、均一的。
|
|
表 2 定海各月降水量的订正值 Table 2 Adjusting values for each month of Dinghai |
图 3为六安 (58311) 降水分析结果。选取合肥 (58321)、霍山 (58314)、滁州 (58236) 和巢湖 (58326) 作为参考台站建立参考序列。
由图 3可以看到, 比值序列在20世纪90年代初起比值偏低, 粗略地看到有一个不连续点; 而从Ts图上可以看到有一个明显的不连续点, 发生在1990年, 最大值为7.453, 超过0.1的显著性水平, 但没有超过0.05的显著性水平。通过查看历史沿革资料, 该站在1962年发生迁站, 海拔高度由39.5 m变为现在的60.5 m, 但在1990年却没有发现任何变化。
对于英山 (58402), 选取了麻城 (57399)、安庆 (58424)、巢湖 (58326) 和黄石 (58407) 作为参考台站建立参考序列, 作出其比值和Ts值序列 (图 4)。可以看到, 比值序列在1996年以后, 明显减小; 从Ts值序列来看, 1996年为一峰值点, 超过了0.05的显著性水平。从图 4上还看到另一个峰值点出现在1964年, 超过了0.1的显著性水平。为了防止此前还存在另一个不连续点被屏蔽掉, 本文将1961—1995年段序列重新进行了检验, 结果显示, 最大值为6.25 (对于n=35, 该值没有达到0.1的显著性水平), 这说明第二个次大值并不存在显著的不连续点。
同样地, 将上述其他台站应用SNHT检验方法进行检验, 在参与检验的36个台站中发现有8个站 (58040, 58122, 58138, 58150, 58343, 58402, 58407, 58477) 有不连续点, 除去常州 (58343) 的1962年不连续点由于接近起始年份, 可以视为虚假不连续点, 还有7个站年降水量序列可能存在不连续点。
SNHT还提供了对检测出的不连续点的订正值[12]。在本文中, 比值的两个均值可以由下式来计算:
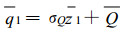
|
(8) |

|
(7) |
序列是参考序列和待检查序列的差值或比值, 比值出现不连续点, 不连续点前后的比值均值不同即q1和q2。订正调整的目的是为了让不连续点前后的q达到一致 (即q2-q1接近于0或者q2/q1接近于1)。如果用差值, 那么订正值就是q2-q1, 而若用比值 (本文中) 检验, 则订正值为q2/q1。这样对于1到a年的订正值就是q2/q1, 假设序列中只有一个不连续点, 那么应用了上述订正值后的序列就可以认为是均一的; 两个以上的不连续点则用同样的方法一一加以订正。
2.4 对检验结果补充判断不同于气温资料, 降水数据的空间变率相对较大, 因此在使用SNHT方法对台站网络进行均一性检验时, 往往要求站网中台站密度达到相当水平, 以保证各个站点序列之间相关性达到相当高的水平, 从而保证检验结果的可靠性。通常可以选用的方法是:参考检验结果, 查看台站历史沿革数据 (也称之为元数据) 信息, 如果元数据反映出在那些可疑点附近发生了台站迁移、仪器换型等影响均一性的变化, 那么这个可疑点很有可能就是真正的非均一点, 反之则需要进一步从数据序列本身去考察是否是人为干扰或者统计方法的不当造成的。从这个角度来看, 并没有发现上述8个站在可疑点附近的元数据变化, 也就是说, 仅仅从统计上发现观测序列相对于临近站 (这个临近站的选取是关键) 而言, 可能存在不连续点。因此, 上述的不连续点是否都是真正意义上的非均一性不连续点, 还需要进一步进行确认和判断。
从2.1节中各站点和其对应的参考站点的相关性 (年降水序列) 来看, 平均相关系数达到了0.763, 但和Alexanderson[12]提出的0.8~0.9比起来还是存在着一定的差距, 如果选定站网进一步加密, 那么待检站和其对应的参考台站相关性会更好。Dai等[19]指出:站点降水序列的非均一性将在历年12个月降水量资料的EOF分解的时间系数的年代际变化中得以体现。因此, 本文通过对历年12个月降水量进行EOF展开的时间系数进行突变性检测, 以补充判断上述检验结果的合理性。
考虑到我国月降水资料的非正态分布, 首先对月降水数据进行了开三次方处理, 以达到一定程度上正态化 (图略)。然后对超过0.05显著水平的几个台站进行检验, 看看上述几个站点降水序列本身是否体现了明显的非均一性。检验结果表明, 除了定海 (58477) (图 5) 以外, 其余几个站点从EOF展开的时间序列来看, 并没有发现显著的突变信号。通过对比认为:上述的检验得到的可疑点是虚假的, 虚假不连续点出现的来源有: ①参考序列的质量问题; ②检验统计手段的系统性偏差等等。从定海数据EOF展开的时间系数可以看出, 在20世纪70年代初期明显有一个突然变化, 结合前面的临近站点的比较检验, 可以认为是非均一性因素所导致的。

|
|
| 图 5. 定海站月降水 (经5年滤波) EOF展开第一时间系数 Fig 5. The first time coefficients of EOF of the monthly precipitation (5 years filtered) for Dinghai | |
3 对月降水量的订正
国际上许多气候序列均一化的工作都采取这样的思路[11, 21] :即对年序列进行检验得出订正值, 然后分别把订正值按各月的实际情况分配到各月, 这样达到对所有月份降水资料进行订正的目的。故本文也采取这一途径, 对定海的降水序列进行订正。
根据表 1, 1970年显著性水平为0.05的不连续点, 年降水量在该点的订正值为1.2, 采取上述订正思路, 计算得出各月的订正参考值 (表 2), 显然, 各月的订正值和年降水量的订正值还是有一定差别的。比较各月的订正值, 发现以8月 (1.43)、9月 (1.52)、10月 (1.49) 的订正幅度较大, 其余月份订正幅度和年降水量订正幅度较一致 (3月、5月、6月、11月), 但也有个别月份 (2月、4月) 出现与年降水量订正方向相反的情况。根据长江三角洲地区降水主要集中在夏半年 (5—10月) 的特点, 以上的订正显然是有一定道理的, 观测或其他因素的改变, 往往可能对原本降水较少月份带来的影响也比较小, 至少是在年降水量的检验中难以体现出来, 因此这种检验和订正对降水量较多的月份、年份给予了较多的权重。这一点Woodley在对英国降水资料进行检验时也得出了同样的结果[22], 以上结果也同时表明, 对逐月序列进行统一订正显然是不合理的。以上订正调整值应用于各个月份序列, 就可以得出相对较为均一的逐月降水量序列。图 6是订正前、后的年降水量序列, 订正后1970年前年降水量数据有所调整, 比订正调整前有所增加, 但从总的趋势上并没有太大的改变。显然, 订正后序列对于序列非均一性的消除是有意义的。

|
|
| 图 6. 订正前 (虚线)、后 (实线) 的年降水量变化曲线 Fig 6. Raw (dashed line) and adjusted (soid line) annual precipitation curves | |
4 结论与讨论
标准正态性均一性检验方法 (SNHT) 是一个相对较为简便、应用效果优秀的检验方法, 它在检验的精确性上相对其他一些方法有其独到的优势; 一般认为, 服从正态分布的气象要素可以直接采用该方法进行检验, 而类似月降水等不服从正态分布的气象要素则必需对资料序列进行一定的处理, 才能采用本方法。
本文基于SNHT方法应用上的优点, 同时考虑我国台站观测实际, 提出了另一种独立于台站密度的研究思路对SNHT方法进行补充的研究思路, 在一定程度上可以对原始数据集中那些明显非均一的序列进行订正调整, 以达到整个数据集基本均一的目的, 该思路对于其他要素也具有一定的参考意义。
检验表明:长江三角洲地区降水资料序列中存在着一定程度的非均一性现象, 在作气候资料整编或气候分析 (特别是单站降水变化分析) 时必需考虑到这一点。均一性检验和订正的最主要目标是获取一套尽可能均一的检验和订正参考序列, 而对于降水量资料由于其时间和空间的不连续性非常明显, 因此参考序列的质量要求资料站点密度尽可能大, 因此, 必需收集尽可能密的台站网络资料来进行均一性研究。长江三角洲地区降水量序列中的不连续点在沿革变化中并没有找到相应的变化, 这和温度序列中不连续点出现与台站迁移关系密切有所不同[10], 因此, 出现不连续现象的原因有待于进一步研究。
致谢 感谢美国国家气候资料中心的Mathew Menne在SNHT方法的应用中的合作。| [1] | Peterson T C, Easterling D R, Karl T R, et al. Homogeneity adjustments of in situ atmospheric climate data:A review. Int J Climatol, 1998, 18: 1493–1517. DOI:10.1002/(ISSN)1097-0088 |
| [2] | Herzog J, Muller W G. Homogenlzation of Various Climatological Parameters in the German Weather Service∥Proceedings of the First Seminar for Homgenlzation of Surface Climatological Data. 1996:101-111. |
| [3] | Olga E Pakhaliuk.Methods of Testing the Homogeneity of Climatological Time Series of National Hydrometeorological Service of UKRAINE∥The fifth International Meeting on Stastical Climatology, 1992:97-100. |
| [4] | WMO. Calculation of Monthly and Annual 30-year Standard Normals. WMO-TD/No.341, Geneva:WMO, 1989. |
| [5] | 李庆祥, 刘小宁, 张洪政, 等. 定点气候序列的均一性研究. 气象科技, 2003, 31, (1): 2–12. |
| [6] | 翟盘茂. 中国历史探空资料中的一些过失误差及偏差问题. 气象学报, 1997, 55, (5): 563–572. |
| [7] | 黄嘉佑, 李庆祥. 一种诊断序列非均一性的新方法. 高原气象, 2007, 26, (1): 62–66. |
| [8] | 刘小宁. 我国40年年平均风速的均一性检验. 应用气象学报, 2000, 11, (2): 27–34. |
| [9] | 李庆祥, MatthewJ Menne, ClaudeN Williams, 等. 利用多模式对中国气温序列中不连续点的检测. 气候与环境研究, 2005, 10, (4): 736–742. |
| [10] | Li Qingxiang, Liu Xiaoning, Zhang Hongzheng, et al. Detecting and adjusting on temporal inhomogeneity in Chinese mean surface air temperature dataset. Adv Atmos Sci, 2004, 21, (4): 260–268. |
| [11] | 李庆祥, 李伟. 近半个世纪中国区域历史气温网格数据集的建立. 气象学报, 2007, 65, (2): 293–300. |
| [12] | Alexanderson H, A homogeneity test applied to precipitation data. J Climatol, 1986, 6: 661–675. DOI:10.1002/joc.v6:6 |
| [13] | Potter K W, Illustration of a new test for detecting a shift in mean precipitation series. Mon Wea Rev, 1981, 109: 2040–2045. DOI:10.1175/1520-0493(1981)109<2040:IOANTF>2.0.CO;2 |
| [14] | Hawkins P M, Testing a sequence of observations for a shift in random location. J Am Statist Assoc, 1977, 73: 180–185. |
| [15] | Alexanderson H.A Homogeneity Test Based on Ratios and Applied to Precipitation.Report 79, Department of Meteorology, Uppsala, 1984:55-60. |
| [16] | Alexanderson H. Homogeneity Testing Multiple Breaks and Trends∥Proceedings of the Sixth International Meeting on Statistical Climatology, Galway, 1995, 439-441. |
| [17] | Alexanderson H, Morberg A, Homogenization of Swedish temperature data, Part Ⅰ:Homogenuity test for Linear Trends. Int J Climatol, 1996, 17: 25–34. |
| [18] | Heikki Tuomenvirta, Alexanderson Hans. Review on the Methodology of the Standard Normal Homogeneity Test (SNHT)∥Fifth International Meeting on Stastical Climatology, 1992:35-44. |
| [19] | Dai Aiguo, Fung I Y, Del A D Genio, et al. Surface observed global land precipitation variations during 1900—88. J Climate, 1997, 10: 2943–2962. DOI:10.1175/1520-0442(1997)010<2943:SOGLPV>2.0.CO;2 |
| [20] | Lindgren B W.Statistical Theory, Macmillan, 1968. |
| [21] | Esterling D R, Peterson T C, A new method for detecting undocumented discontinuities in climatological time series. Int J Climatology, 1995, 15: 369–377. DOI:10.1002/(ISSN)1097-0088 |
| [22] | Woodley M R, Recent changes in summer rainfall values measured at Long Aston. Weather, 1985, 40: 180–188. DOI:10.1002/wea.1985.40.issue-6 |
| [23] | 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 2003. |
 2008, 19 (2): 219-226
2008, 19 (2): 219-226



