应用气象学报  2008, 19 (1): 10-18   PDF    
引用本文
朱宗申, 朱国富. 有限区域风速场求解流函数和速度势场的有效方案[J]. 应用气象学报, 2008, 19(1): 10-18.
Zhu Zongshen, Zhu Guofu. An Effective Method to Solve the Streamfunction and Velocity Potential from a Wind Field in a Limited Area[J]. Journal of Applied Meteorological Science, 2008, 19(1): 10-18  
有限区域风速场求解流函数和速度势场的有效方案
朱宗申1,2, 朱国富1,2     
1. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
2. 国家气象中心, 北京 100081
2006-12-29 收到, 2007-07-31 收到修改稿.
资助项目: 国家自然科学基金项目 (40475042) 和国家“十一五”科技支撑计划项目“灾害天气精细数值预报系统及短期气候集合预测研究” (2006BAC02B) 共同资助    
摘要: 流函数和速度势是表示风场的一种变量, 在数值天气预报模式和分析、同化方案中经常使用, 通常可以用风速分量场求解Poisson方程得到。对于有限区域系统, 往往采用差分方法, 但由于存在边界问题, 用计算所得到的流函数和速度势场重建风速场, 在边界附近经常出现明显的偏差。基于差分方法、利用有限区域风速场求解流函数和速度势场的基本方法和特点的分析, 在Arakawa A网格分布的有限区域, 设计了一种用差分方法求解流函数和速度势场的有效方案。在该有效方案中, 通过将有限区域向外扩展二圈, 风速场线性外推, 改进计算边界风速值和边界定解条件的效果; 尽可能使用协调、一致的差分格式, 提高求解精度; 最后利用一种增量订正迭代方法, 迭代2~3次就可以获得令人满意的结果。实例试验的对比、检验显示, 用该方案计算求得的流函数和速度势场重建风速场, 具有非常高的精度。
关键词: 有限区域    流函数和速度势    差分计算方案    风场分离和重建    增量订正迭代方法    
An Effective Method to Solve the Streamfunction and Velocity Potential from a Wind Field in a Limited Area
Zhu Zongshen1,2, Zhu Guofu1,2     
1. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
2. National Meteorological Center, Beijing 100081
Abstract: The streamfunction and the velocity potential are variables commonly used in the scheme design for atmospheric data assimilation and initial field analysis of numeric weather prediction.They can be obtained in partitioning a wind field by solving the Poisson equations of the vorticity and the divergence of the horizontal components of the wind field. Difference method is usually adopted in a limited area; nevertheless, an obvious departure exits between the original wind field and the reconstructed one from the sum of the streamfunction and velocity potential components in the vicinity of the boundary of the limited area. An effective scheme is designed to solve by difference method the streamfunction and velocity potential of a wind field in an Arakawa-A grid limited area, based on analyzing detailedly the approach and characteristics in the process of the solution. The key techniques in the scheme include the following. Firstly, the solution domain is expanded by two rings by extrapolating linearly the wind field to improve a calculation of boundary values. Secondly, consistent difference schemes are introduced in the solution procedure to enhance the solution precision. And finally only two to three iterations are imposed on incremental corrections to get a satisfactorily accurate result. Experiments are carried out with real wind data and their results indicate that the streamfunction and velocity potential of a wind field can be acquired by the scheme and the reconstructed wind field is reproduced with a very high precision.
Key words: limited area     streamfunction and velocity potential     difference scheme     partition and reconstruction of wind field     iterative method of incremental correction    
引言

流函数和速度势是表示风场的一种变量, 在数值天气预报模式和分析、同化方案中经常使用[1-3], 通常可以用风速分量场求解Poisson方程得到。对于全球系统, 容易采用谱方法获得; 对于有限区域系统, 往往采用差分方法。在有限区域求解流函数和速度势场的方法曾有不少研究[4-8], 但由于存在边界问题, 利用计算所得到的流函数和速度势场重建风速场时, 边界附近经常出现明显偏差。Chen等[9-10]研究用谱方法求解的方案, 给出很好的结果。本文提出一种较以往方案具有更高精度的差分计算求解方案。

1 有限区域风速场分离流函数和速度势场的基本原理 1.1 风速场计算流函数和速度势场的方法

设在有限区域Ω, 其水平纬向、经向风速分量为u, v, 存在流函数、速度势为Ψ, χ; Ω内的涡度、散度分别表示为ζ, η。有

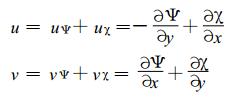
(1)
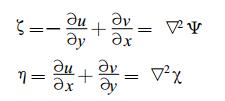
(2)

其中, uΨ, vΨ和uχ, vχ分别为有旋风速和散度风速分量。如果己知有限区域Ω边界∑的Ψ, χ值为:

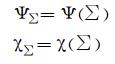
(3)

此时, 由有限区域u, v场, 根据式 (2), (3) 求解流函数和速度势场是典型的Poisson方程第一边值问题, 采用超松弛迭代方法, 可以得到有限区域内的流函数和速度势场的唯一解。

1.2 风速场求解流函数和速度势场方法的一些特点

在有限区域, 用初始风速u, v场求解Poisson方程获得流函数和速度势场的方法, 有如下一些特点。

1.2.1 解的非唯一性

在有限区域利用u, v场求解流函数和速度势场的实际问题中, 往往仅知道区域Ω内及其边界∑的风速值, 并不知道∑的Ψ, χ值。此时, 求解问题的边界条件变为:

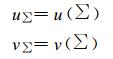
(4)

根据式 (1) 和式 (4) 式得到:

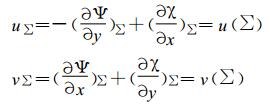
(5)

由式 (5) 可以得到无数个定解边界条件式 (3) 的解。所以, 利用u, v场求解得到的满足方程式 (2) 和边界条件式 (5) 的流函数和速度势场不是唯一的。

1.2.2 重建风速场的确定性

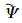
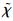
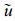
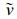
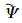
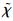
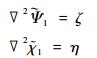
文献[9]曾讨论过以下用流函数和速度势场的解重建风速场的问题。利用1.2.1节, 由有限区域Ω的u, v场求解得到的流函数和速度势场, 根据式 (1) 可以重建风速, 场 (上标~表示计算值, 下同)。设其中的一个特解为1和1, 在有限区域Ω内有:

(6)

在边界∑有:

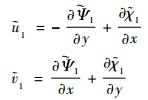
(7)

则重建风速场有:

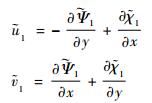
(8)

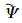
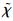
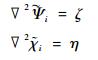
如果任意的另一个特解为 i和i, 在有限区域Ω内有:

(9)

在边界∑有:

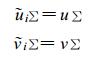
(10)

则重建风速场有:

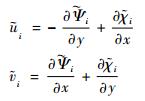
(11)

设

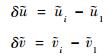
(12)

由式 (12) 和 (8)、(11)、(6)、(9), 在有限区域Ω内有:

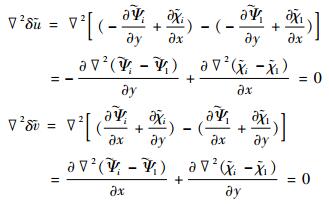
(13)

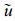
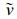
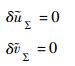
因此, δ和δ 仅可能在区域Ω的边界有极值。由式 (7)、(10) 和 (12), 边界条件为:

(14)

所以,

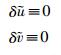
(15)

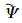
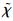
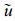
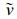
据此, 虽然由u, v场求解得到的和场不是唯一的, 但是用它们重建的风速, 场是唯一确定的。

1.2.3 差分计算格式的一致性

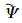
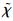
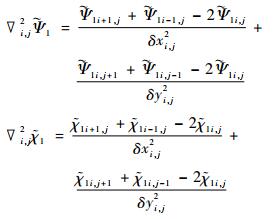
在有限区域用Poisson方程计算和场, 往往采用差分方法。由式 (5) 分别得到式 (3) 的定解边界条件 (见2.1节) 后, 根据式 (2) 求解得到。式 (2) 右端可以采用如下两种差分形式方案计算:

(16)

或

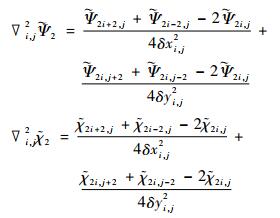
(17)

式 (2) 左端利用初始u, v场按下式计算:

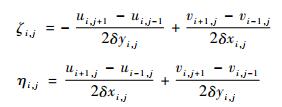
(18)

对于风速计算, 通常采用中央差分的方法:

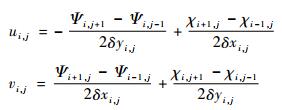
(19)

此时, 式 (18) 可改写为:

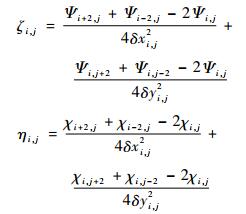
(20)

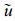
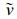
将式 (16), (17) 与式 (20) 对比可见, 与方案1的式 (16) 不同, 方案2的式 (17) 与用计算风速的式 (19) 得到ζ, η的式 (20) 具有一致的差分格式形式。实例试验 (见3.1.1节) 显示, 求解方案的差分格式尽可能与用初始风速计算ζ, η的差分格式一致, 对求解结果有很大的影响, 可以明显减小重建风速, 场与初始风速u, v场之间的偏差。

1.2.4 区域边界差分计算格式的不协调和误差

受区域边界的限制, 在边界地区用差分方法进行计算时有可能产生类似1.2.3节的计算格式不协调问题, 从而影响计算结果的精度, 出现重建风速场的误差。其主要出现在以下几个计算步骤中:

①在区域内邻近边界的一圈进行Poisson方程求解计算时, 由于缺少区域外的流函数和速度势的值, 因此无法采用式 (17), 仅能采用或部分采用 (对垂直于边界方向的差分计算) 与用风速场计算差分格式不完全一致的式 (16) 方案。

②边界的风速值 (包括有旋风和散度风), 同样由于缺少区域外的流函数和速度势的值, 无法完全采用式 (19) 求得, 往往只能使用外推方法。

③即使获得正确的边界散度风速值, 由于受格点网格方案的限制, 用边界风速值推求求解Poisson方程的定解边界条件时, 有时也无法避免采用某些插值、平均等近似计算方法 (如Arakawa A网格方案, 见2.1节)。

2 有限区域风速场求解流函数和速度势场的方案

在一个等经、纬度格点和Arakawa A网格分布[11]的有限区域, 设计了一种使用差分方法、利用初始风速u, v场求解流函数和速度势场的方案, 可以明显提高重建风速场的计算精度。

2.1 方案的计算步骤

方案将采用上述公式的球面坐标差分计算形式。主要计算步骤如下:

①为了减少边界的影响, 将有限区域向外扩展二圈, 原区域的u, v场线性外推至扩展区域, 在扩展后的有限区域进行求解。用u, v场按式 (18) 计算区域内的ζ, η场。

②采用文献[9]相似的方法, 根据下式:

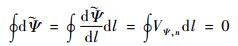
(21)

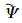
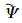
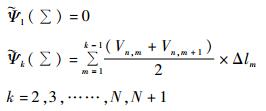
计算的定解边界条件。用扩展区域边界相邻格点的法向风速Vn(u或v) 的平均值作为近似的边界法向有旋风速V Ψ, n, 利用差分方法计算边界的 k :

(22)

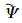
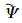
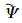
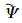
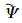
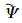
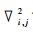
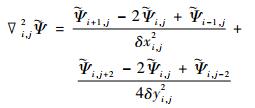
其中, Δl为格距, N为边界格点数; 通过调整k(∑), 使得绕边界线积分一圈后回到第一格点的n+1(∑) 等于 1(∑), 得到的定解边界条件。然后, 在扩展后的有限区域, 用ζ场和边界条件(∑) 求解Poisson方程得到场。其中Ψ, 尽可能采用与风速计算一致的式 (17), 除邻近区域边界内的一圈:4个角的格点采用式 (16), 其他格点采用式 (16)、式 (17) 的组合, 即邻近东、西边界的格点采用下式

(23)

邻近南、北边界的格点采用下式

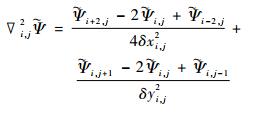
(24)

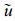
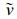
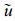
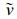
最后, 计算区域内的有旋风速Ψ和 Ψ场, 无法用中央差分计算的部分边界Ψ, ∑和Ψ, ∑值线性外推得到。

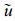
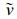
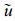
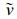
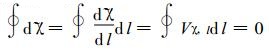
③用边界风速∑, ∑减去有旋风速Ψ, ∑, Ψ, ∑, 得到近似的沿区域边界的切向散度风速Vχ, l (uχ, ∑或v χ, ∑)。再采用上述计算流函数相似的方法, 根据下式:

(25)

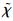
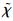
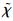
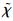
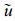
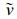
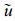
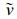
由Vχ, l计算和调整得到扩展区域的的定解边界条件(∑); 然后, 用η场和(∑) 求解Poisson方程得到区域内的场, 以及计算散度风速χ和 χ场, 无法用中央差分计算的部分边界χ, ∑和 χ, ∑值线性外推得到。

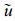
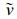
④由计算得到的有旋风速和散度风速场合成全风速, 场, 用下面的式 (26) 和式 (27) 求它们与初始风速u, v场的偏差。利用研制的一种求解流函数和速度势场的增量订正方案 (见2.2节), 通过迭代计算修正边界条件, 采用增量方法减小计算误差, 最终获得满足风速场精度要求的流函数和速度势场。

2.2 求解流函数和速度势场的增量订正迭代方案

经过多种计算区域选择方案的试验、对比, 确定增量订正迭代方案的计算在扩展一圈的有限区域进行。

2.2.1 基本变量

设:

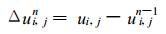
(26)
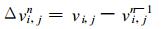
(27)
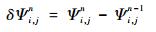
(28)
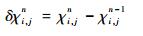
(29)
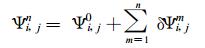
(30)
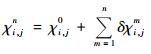
(31)
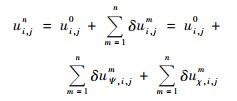
(32)
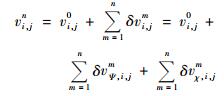
(33)

其中, Δ表示偏差; δ表示增量; 无上标的ui, j, vi, j为初始风速; 上标0表示迭代前的计算结果; 上标n表示迭代后的计算结果, n=1, 2, ……, N为迭代次数。

2.2.2 增量订正计算公式

根据式 (2), 有

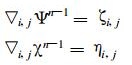
(34)
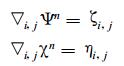
(35)

则由式 (28)、(29) 得到增量订正差分方程为

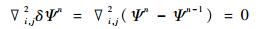
(36)
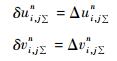
(37)

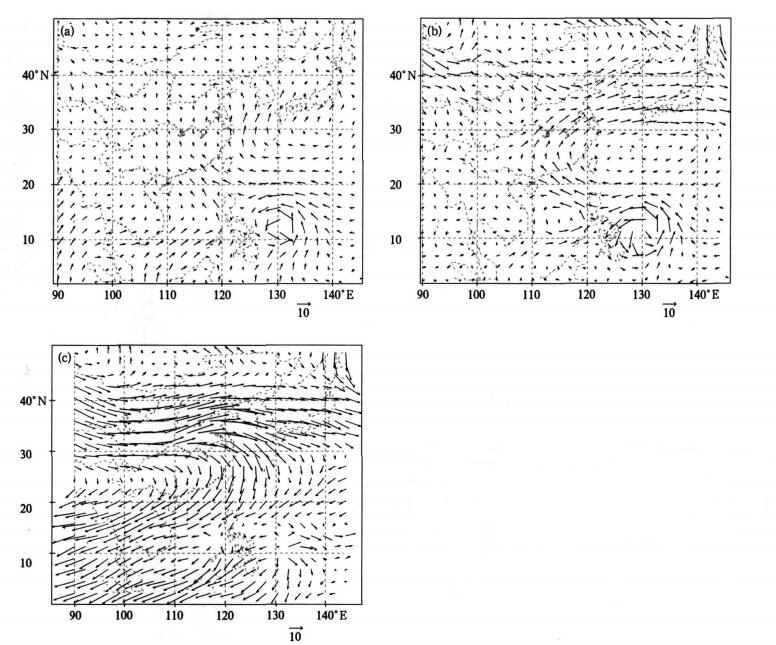
迭代边界条件取:

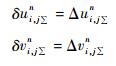
(38)

其中,

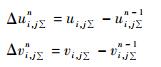
(39)

采用类同于上述用u, v场计算Ψ和χ场的定解边界条件的方法, 分别用风速偏差Δun和Δvn场计算δ Ψ n和δ χ n场的定解边界条件δ Ψ n(∑) 和δ χ n(∑)。利用边界条件分别求解增量订正差分方程式 (36) 和 (37), 得到区域内的增量δΨ n和δ χ n场, 并根据式 (30), (31) 求得订正的Ψn, χ n场。

2.2.3 迭代计算

采用式 (19), 利用增量δ Ψ n和δ χ n场获得区域内的δ uΨn, δ vΨn和δ uχn, δ vχ n场, 无法用中央差分计算的部分边界值由线性外推得到; 并由式 (32), (33), 得到订正的合成风速un, v n场。再由式 (26), (27), 得到下一迭代步的风速偏差场, 重复上述过程迭代至N次, 或满足Δun, Δv n的精度要求时, 即中止。

3 实例试验

利用实际风速场资料进行方案的计算, 由求得的流函数和速度势场重建原区域风速场, 与初始风速场作对比、检验。

3.1 个例测试

使用国家气象中心中期数值预报系统T213 12 h预报的2003年7月20日12:00(世界时, 下同) 1000 hPa, 500 hPa和150 hPa u, v场资料, 对不同的差分格式、计算区域和增量订正迭代的方案进行试验。试验区域范围为2.25°~49.50°N, 90.00°~144.00°E, 分辨率为0.5625°×0.5625°等经、纬度, 网格点为Arakawa A分布。图 1给出水平风速场, 图 2是对应的流场。

图 1. 2003年7月20日12:00的水平风速场 (单位: m·s-1) (a)1000 hPa u, (b)1000 hPa v, (c)500 hPa u, (d)500 hPa v, (e)150 hPa u, (f)150 hPa v Fig 1. Components of wind speed at 12:00 on July 20, 2003 (unit:m·s-1) (a) u at 1000 hPa, (b) v at 1000 hPa, (c) u at 500 hPa, (d) v at 500 hPa, (e) u at 150 hPa, (f)v at 150 hPa

图 2. 2003年7月20日12:00的流场 (单位:m·s-1) (a)1000 hPa, (b)500 hPa, (c)150hPa Fig 2. Wind fields at 12:00 on July 20, 2003(unit:m·s-1) (a)1000 hPa, (b)500 hPa, (c)150hPa

3.1.1 差分格式影响

对于风速的计算, 均采用式 (19) 中央差分的方法。Poisson方程的计算, 取如下3种差分格式进行试验比较。方案1采用式 (16) 形式, 取一倍格距间隔要素值; 方案2, 3, 在区域内部均采用式 (17) 形式, 取二倍格距间隔要素值, 但对于邻近边界的一圈:方案2采用式 (16), 方案3采用式 (16) 和式 (23), (24) 形式, 沿边界切向尽可能取二倍格距间隔要素值。

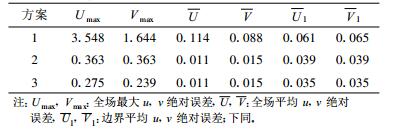
表 1, 2给出在扩展二圈区域, 求解Poisson方程时采用上述3种不同差分格式, 迭代前和进行增量订正、迭代3次后的500 hPa计算结果。

表 1 计算Poisson方程时采用3种不同差分格式方案迭代前得到的500 hPa风速绝对误差比较 (单位:m·s-1) Table 1 The comparison of absolute errors between wind speeds and their reconstructed ones from three difference schemes in solving the Poisson equations without any iteration correction at 500 hPa (unit:m·s-1)

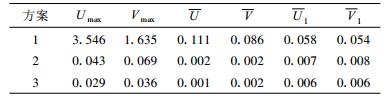
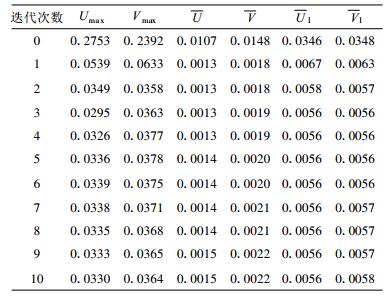
表 2 计算Poisson方程时采用3种不同差分格式方案迭代3次后得到的500 hPa风速绝对误差比较 (单位:m·s-1) Table 2 Same as in Table 1, but with three-iteration corrections

试验对比显示: Poisson方程计算采用不同的差分格式对重建风速场的精度有明显影响, 与风速计算格式较为一致的方案3具有最好的结果。

如下试验均选取上述较好的第3种差分格式方案。

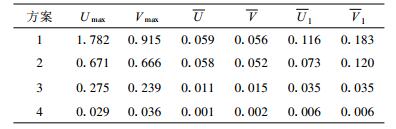
3.1.2 计算区域选择

采用如下4种方案: ①不扩展区域和不进行增量订正; ②不扩展区域和进行增量订正、迭代3次; ③扩展区域和不进行增量订正; ④扩展区域和进行增量订正、迭代3次进行比较。500 hPa的计算结果见表 3。

表 3 4种不同计算方案的500 hPa风速绝对误差比较 (单位:m·s-1) Table 3 Same as in Table 1, but their reconstructed ones from four difference schemes in expanding the solution domain and adding iteration corrections (unit:m·s-1)

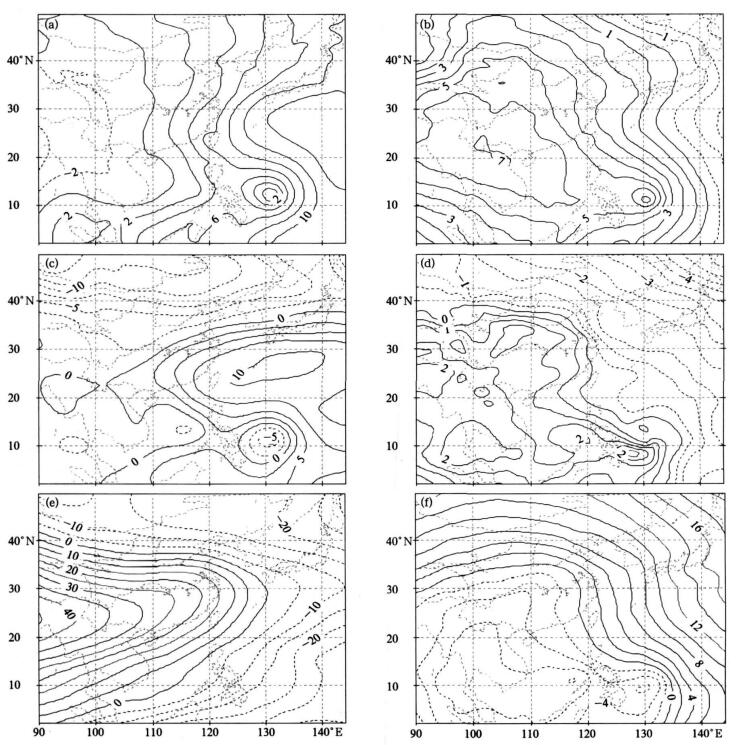
由表 3可知, 扩展区域对于计算精度提高非常重要, 同时采用增量订正迭代能更好改进计算效果; 设计的“最佳”方案4给出最好的结果。图 3是方案4计算得到的1000 hPa, 500 hPa和150 hPa流函数、速度势场。

图 3. 2003年7月20日12:00的流函数和速度势场 (单位: 106m2·s-1) (a)1000 hPa Ψ, (b)1000 hPa χ, (c)500 hPa Ψ, (d)500 hPa χ, (e)150 hPa Ψ, (f)150 hPa χ Fig 3. Streamfunctions (Ψ) and velocity potentials (χ) at 12:00 on July 20, 2003 (unit:106m2·s-1) Ψ at 1000 hPa, (b)χ at 1000 hPa, (c)Ψ at 500 hPa, (d)χ at 500 hPa, (e) Ψ at 150 hPa, (f)χ at 150 hPa

3.1.3 增量迭代订正效果

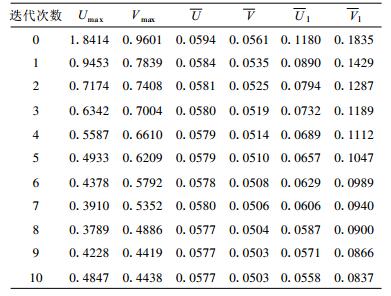
表 4, 5分别给出不扩展区域方案和扩展区域方案迭代10次的500 hPa风速场计算结果。迭代过程提高计算精度; 迭代1~2次后, 误差迅速减小, 以后基本保持平稳; 通常迭代2~3次就可以取得很好的效果, 但并不完全能够表明计算收敛。扩展区域方案的迭代过程, 对计算精度改进非常明显。

表 4 不扩展区域方案迭代10次计算得到的风速绝对误差 (单位:m·s-1) Table 4 Same as in Table 3, but for ten-iteration corrections without expanding the solution domain (unit:m·s-1)

表 5 扩展区域方案迭代10次计算得到的风速绝对误差 (单位:m·s-1) Table 5 Same as in Table 4, but for ten-iteration corrections with expanding the solution domain (unit:m·s-1)

对于1000 hPa和150 hPa的计算有着完全相似的结果。迭代3次后重建的全风速场与初始风速场的最大偏差还不到0.06和0.05 m·s-1。

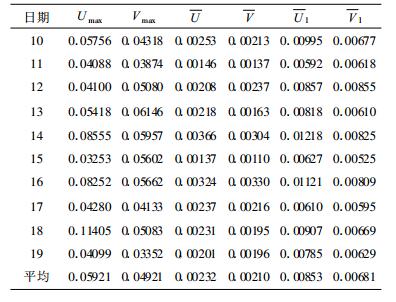
3.2 统计效果检验

使用国家气象中心中期数值预报系统T213 12 h预报的2006年7月10—19日12:00的500 hPa u, v场资料进行试验, 并对方案效果作检验。试验区域、分辨率和网格分布与个例试验相同。表 6给出扩展区域和订正迭代3次的方案每天的全场最大、全场平均和边界平均u, v绝对误差, 以及它们的10 d平均。统计结果和个例测试相似, u, v 10 d平均的全场最大绝对误差低于0.06 m·s-1, 具有很高的精度。

表 6 2006年7月10—19日12:00 10 d 500 hPa风速绝对误差及统计结果 (单位:m·s-1) Table 6 Same as in Table 3, but for ten days from 10 to 19 July 2006 and their average, according to the scheme of expanding the solution domain and adding three-iteration corrections (unit:m·s-1)

4 总结和讨论

根据“用有区域风速分量场求解流函数和速度势场非唯一性, 以及这些流函数和速度势场却能够重建确定风速场”的特点, 研制了采用差分方法求解流函数和速度势场的有效方案。其主要特点为:

1) 将有限区域向外扩展二圈, 风速场线性外推, 以此减小边界的影响, 改进获取边界风速值和确定边界定解条件的计算效果。

2) 尽可能采用与计算风速和涡度、散度协调一致的差分格式, 提高求解Poisson方程的计算精度。

3) 分别在扩展二圈的区域采用传统方法, 求解一级近似的流函数和速度势场。

4) 在扩展一圈的有限区域采用增量订正迭代方法, 通过迭代计算修正边界条件, 采用增量方法减小计算误差, 对一级近似的流函数和速度势场加以订正。通常迭代2~3次就可以获得令人满意的结果。

5) 使用实际资料进行试验, 在原区域用重建的风速场与初始风速场对比、检验显示, 计算结果具有非常高的精度。

方案计算结果依然存在一定的误差, 并且迭代过程未必一定收敛。对方案进行分析发现, 由于受有限区域边界和网格自身条件的限制, 不能采用格式完全协调、一致的差分方案来精确计算边界风速值、定解边界条件和求解Poisson方程, 这可能是其最主要的原因。对利用有限区域风速分量场, 用差分方法求解流函数和速度势场方案的误差研究, 将在另文中进一步阐述。

参考文献
[1] Lorenc A C, Ballard S P, Bell R S, et al. The Met Office global three-dimensional variational data assimilation scheme. Q J R Meterorol Soc, 2000, 126: 2991–3012. DOI:10.1002/(ISSN)1477-870X
[2] Barker D M, Huang W, Guo Y R, et al. A three-dimensional (3DVAR) data assimilation system for use with MM5: Implementation and initial results. Mon Wea Rev, 2004, 132: 897–914. DOI:10.1175/1520-0493(2004)132<0897:ATVDAS>2.0.CO;2
[3] 朱宗申, 胡铭. 一种区域格点三维变分分析方案——基本框架和初步试验. 大气科学, 2002, 26: 684–694.
[4] Shukla J, Saha K R, Computation of non-divergent streamfunction and irrotational velocity potential from the observed winds. Mon Wea Rev, 1974, 102: 419–425. DOI:10.1175/1520-0493(1974)102<0419:CONDSA>2.0.CO;2
[5] Stephens J J, Johnson K W, Rotational and divergent wind potentials. Mon Wea Rev, 1978, 106: 1452–1457. DOI:10.1175/1520-0493(1978)106<1452:RADWP>2.0.CO;2
[6] Bijlsma S J, Hafkensheid L M, Lynch P, Computation of the streamfunction and velocity potential and reconstruction of the wind field. Mon Wea Rev, 1986, 114: 1547–1551. DOI:10.1175/1520-0493(1986)114<1547:COTSAV>2.0.CO;2
[7] Lynch P, Deducing the wind from vorticity and divergence. Mon Wea Rev, 1988, 116: 86–93. DOI:10.1175/1520-0493(1988)116<0086:DTWFVA>2.0.CO;2
[8] Lynch P, Partitioning the wind in a limited domain. Mon Wea Rev, 1989, 117: 1492–1500. DOI:10.1175/1520-0493(1989)117<1492:PTWIAL>2.0.CO;2
[9] Chen Q S, Kuo Y H, A harmonic-sine series expansion and its application to partitioning and reconstruction problems in a limited area. Mon Wea Rev, 1992, 120: 91–112. DOI:10.1175/1520-0493(1992)120<0091:AHSSEA>2.0.CO;2
[10] Chen Q S, Kuo Y H, A consistency condition for wind-field reconstruction in a limited area and harmonic-cosine series expansion. Mon Wea Rev, 1992, 120: 2653–2670. DOI:10.1175/1520-0493(1992)120<2653:ACCFWF>2.0.CO;2
[11] Arakawa A, Computational design for long-term numerical integrations of the equations of atmospheric motion. J Comput Phys, 1966, 1: 119–143. DOI:10.1016/0021-9991(66)90015-5