2. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
3. 中国科学院研究生院, 北京 100049
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Graduate School, CAS, Beijing 100049
对于干空气, 位温是一个很重要的温度参量, 它在干绝热过程中具有守恒性[1], 所以可用来比较不同气压下空气质块的热力差异, 但是在伴有降水等潜热释放的湿过程中, 位温不再守恒。此时, 人们引入了在湿绝热过程中保持守恒性的相当位温, 相当位温被广泛应用到分析大气的稳定度[2-4]、诊断温带气旋[5-6]、热带气旋[7-8]、飑线[9]、锋面[10-12]、雨带[13-15]及热带对流系统[16-19]等多个领域。与温度相比, 无论是位温还是相当位温, 由于其守恒性, 在大气动力和热力学研究领域都得到了广泛应用。尽管如此, 它们都有各自的适用范围:位温适用于处处干燥的大气, 而相当位温适用于完全饱和的湿空气。然而, 实际大气既不是处处干燥又不是完全饱和, 即是“非均匀饱和”的[20], 两者的适用性受到了限制。还有一个不容忽视的事实就是, 通常当测湿器测得的实际大气相对湿度超过70%时, 大气中的局部地区可能已经有凝结发生了。通常, 相对湿度越大, 水汽越容易发生凝结。也就是说, 凝结随着湿度的增加而增加。Gao等[20]通过考虑水汽梯度效应, 把一个与比湿相联系的变量 (广义位温θ*) 引入到大气热力框架中, 充分体现了实际大气总处于绝对干与完全饱和之间的特性。这个变量的引入没有带来大量的其他变量, 因此很方便用到实际业务中。之后, 又形成了一系列围绕着广义位温的临近动力预报方法, 如广义湿位涡对桑拿天气的识别与预测[21], 非均匀饱和大气中的非地转湿Q矢量对暴雨天气的诊断[22]等。本文旨在引入非均匀饱和大气中的广义位温θ*及在其基础上导出的广义湿位涡来分析暴雨特征, 并期望通过对广义湿位涡异常的诊断来判断暴雨落区, 并进行短时预报。
1 广义湿位涡方程及其异常在本研究中, 对相对湿度很大, 有凝结现象出现但大部分地区并未饱和的区域称为临近饱和区, 而Gao等[20]定义的广义位温θ*引入大气热力框架后, 更适合于描述大气饱和区和临近饱和区的热力特征。由于湿位涡在暴雨研究中有广泛应用, 本节通过引进Gao等[20]定义的广义位温, 将推导出广义湿位涡倾向方程, 并讨论广义湿位涡的异常对暴雨发生的指示意义。
1.1 广义湿位涡及其倾向方程Gao等[20]定义的广义位温θ*表达式为
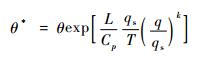
|
(1) |
式 (1) 中, θ是位温, L是凝结潜热系数, T是大气温度, q和qs分别是比湿和饱和比湿, k是与反映大范围凝结状态与局地凝结现象有关的权重函数的计算系数, 参考文献[20], 取k=9。将θ*代入热力学方程, 并引入绝对涡度方程后, 根据吴国雄等[23]的研究, 可得到广义湿位涡的倾向方程:
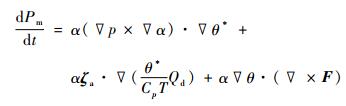
|
(2) |
式 (2) 中, Pm=αζa·∇θ*就是广义湿位涡。
由于α=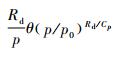
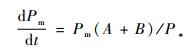
|
(3) |
式 (3) 中, A=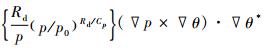
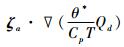
A是由于斜压性与广义位温梯度作用造成的广义湿位涡的生成项, B是非绝热加热导致广义湿位涡的生成项。在绝热条件下, Qd=0;由广义位温θ*的定义可见, 在干大气中, q=0, 此时, θ*=θ, 相应地, 广义湿位涡蜕变为传统的Ertel位涡, 在干绝热大气中是守恒的; 在饱和大气中, q=qs, 此时, θ*=θe, 且有 (∇p×∇α)·θ*=(∇p×∇α)·∇θe=0[23], 此时, 广义湿位涡就蜕变成湿位涡, 在湿绝热饱和大气中也是守恒的。但是, 对包含有水汽但又未有凝结发生的大气 (这种状态更接近于实际大气), 由于Pm不再仅仅是气压、温度的函数, 还与水汽有关, 此时, 它不再是一个守恒量, 这也是广义湿位涡在实际应用中存在的局限性。
1.2 广义湿位涡异常与暴雨发生利用广义位温定义, A可写为
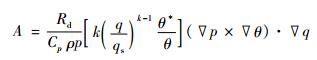
|
(4) |
为了使影响A的因子表示得更为清楚, 可将A的表达式重新整理, 得到:
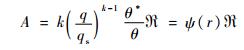
|
(5) |
式 (5) 中, 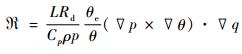
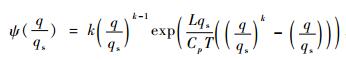
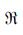
如果取T=300 K, p=1000 hPa, qs=6×10-3 g· g-1, 由ψ(r) 随r变化的曲线 (图略) 可见, 当r < r1(r1=0.53) 时, ψ(r) < 0.05 ≈0, 广义湿位涡不可能生成; 当r < r2(r2=0.7) 时, ψ(r) < 0.5, 广义湿位涡很小; 当r2 < r < r3(r3=0.77) 时, 0.5 < ψ(r) < 1, 广义湿位涡的生成也是可忽略的; 当r >r3时, ψ(r)>1, 并且在q等于qs之前, ψ(r) 随r的增加而急速增大。因此, 广义湿位涡的生成也随r的增加而增加。可见, 在暴雨发生时期, 即使空气还未完全达到饱和, 广义湿位涡也必定出现异常。
从动力上看, 湿绝热大气中广义湿位涡的倾向由斜压作用项与湿度梯度 (式 (2) 和式 (4)) 决定。具体来说, 如果有正 (负) 的广义湿位涡生成, (∇p×∇θ)·∇q就取正 (负) 值, 意味着在比湿梯度方向上的斜压性增加 (减少)。另一方面, 由于广义位温在形式上与相当位温的相似性, 广义湿位涡与湿位涡在稳定性方面有类似的判剧, 即广义湿位涡 < 0是二维条件对称不稳定的充分条件[2-4, 7]。
2 暴雨天气动力识别的诊断分析依据上面分析可知, 高湿环境以及一定的湿度场与水汽场配置及动力形势有利于广义湿位涡发生异常, 因而暴雨天气的发生有利于广义湿位涡出现异常。这是理论上的分析, 但实际情况是否如此需要依据实际观测资料进行动力诊断。本研究对2001年7月26—27日我国华北地区发生的一次强降水过程和2003年7月7—9日湖南、安徽和江苏发生的一次梅雨锋暴雨过程进行了动力诊断, 其目的是考察大气温湿分布以及动力场作用对广义湿位涡生成的作用, 从而确定可否用广义湿位涡异常来识别暴雨天气。
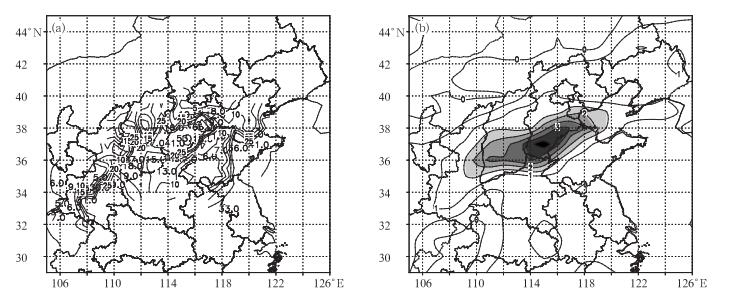
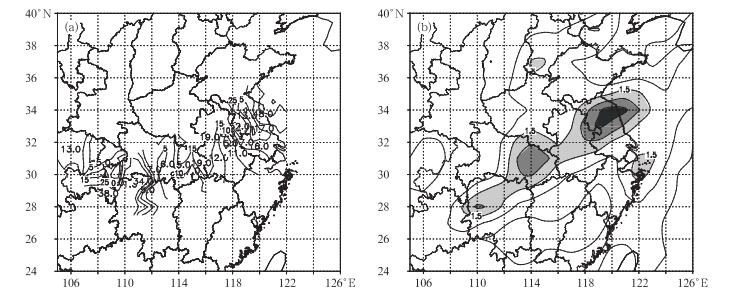
利用NCEP/NCAR的1°×1°格点分析资料计算广义湿位涡, 结果表明, 在975~500 hPa层中, 广义湿位涡的正异常都较明显。图 1是2001年7月27日06:00(世界时, 下同) 地面6 h降水实况和同时刻850 hPa上广义湿位涡分布。图 2是2003年7月9日00:00地面6 h降水实况和925 hPa上广义湿位涡分布。从图 1b和图 2b都可以看出, 在暴雨发生区域广义湿位涡有大值中心对应, 如果取大于1.5为广义湿位涡异常, 华北暴雨的广义湿位涡的正异常区主要位于山东、河北、山西及河南交界区域, 呈偏东—西走向 (图 1b); 而江淮暴雨的广义湿位涡正异常在江苏、湖北和湖南省有3个中心 (图 2b)。可见, 在这两次暴雨过程中, 广义湿位涡异常区主要集中在大气中低层的700 hPa以下, 这与大气中水汽主要分布在700 hPa以下是一致的。从广义湿位涡异常区与降水场分布形势看, 雨带与广义湿位涡异常区域对应都还是比较好的。
|
|
| 图 1. 2001年7月27日06:00地面6 h降水实况 (单位:mm)(a) 与850 hPa广义湿位涡 (单位:PVU; 阴影区是广义湿位涡值≥1.5 PVU的区域, 1 PVU=10 -6K·m3·kg -1·s -1)(b) Fig 1. Horizontal distribution of 6-hour precipitation from observation (unit:mm)(a), generalized moist potential vorticity at 850 hPa (unit:PVU; the shade area represents the generalized moist potential vorticity value≥1.5 PVU)(b) at 06:00 on July 27, 2001 | |
|
|
| 图 2. 2003年7月9日00:00地面6 h降水实况 (单位:mm)(a) 与925 hPa广义湿位涡 (单位:PVU; 阴影区是广义湿位涡值≥1.5 PVU的区域)(b) Fig 2. Horizontal distribution of 6-hour precipitation from observation (unit:mm)(a), generalized moist potential vorticity at 925 hPa (unit:PVU, the shade area represents the generalized moist potential vorticity value≥1.5 PVU)(b) at 00:00 on July 9, 2003 | |
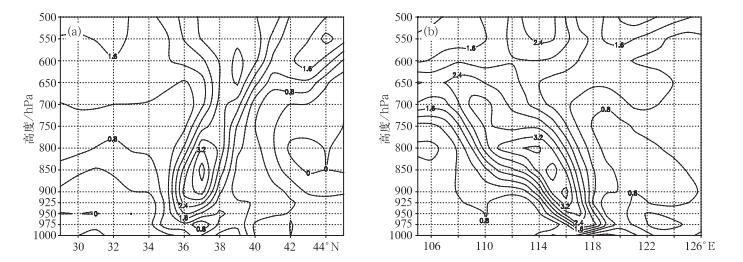
从经过华北暴雨中心的广义湿位涡经向 (取115°E, 图 3a) 和纬向 (取37°N, 图 3b) 垂直剖面分布图上也可以发现, 无论是经向还是纬向剖面, 广义湿位涡的异常大值区域相对集中在暴雨中心及周边地区对流层的中低层, 表明由于中低层水汽的输送与辐合造成暴雨区有充沛的水汽, 大气中的相对湿度增加 (相对湿度增大, 容易与周围相对干的空气形成湿度梯度)。因此, 出现了广义湿位涡的异常, 与上面理论分析结果是一致的。广义湿位涡在江淮梅雨锋暴雨发生时期的经向和纬向垂直分布图上, 也有类似的结果 (图略)。
|
|
| 图 3. 2001年7月27日06:00沿暴雨中心的广义湿位涡沿115°E垂直剖面 (a) 和沿37°N垂直剖面 (b)(单位:PVU) Fig 3. Meridional distribution along 115°E (a) and zonal distribution along 37°N (b) of generalized moist potential vorticity at 06:00 on July 27, 2001(unit:PVU) | |
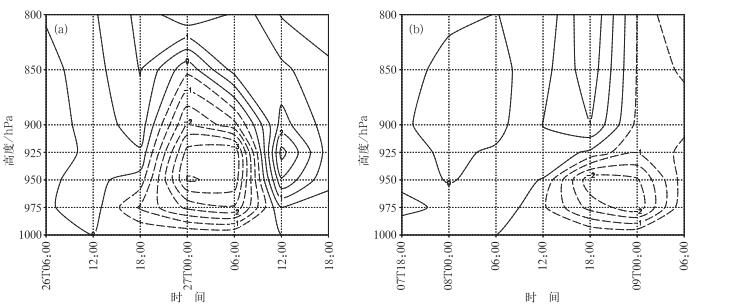
但是, 仅仅指出在暴雨天气发生时广义湿位涡异常有动力识别作用是不够的。如果这种异常在暴雨发生之前就能有所反映, 从而预报出暴雨天气的发生及落区才是最有意义的。因此, 考虑利用广义湿位涡异常的变化趋势来预报暴雨天气的发生与否, 利用式 (4) 的右端项 (即广义湿位涡倾向项) 来计算广义湿位涡的变化, 从而预测暴雨的发生。以2001年华北暴雨为例, 图 4a显示的是37°N, 115°E处不同高度处广义湿位涡倾向的时间演变, 可以明显地看到, 950~900 hPa之间的广义湿位涡倾向从7月26日12:00开始为零, 随后减小为负, 且负值越来越大, 到27日00:06—12:00之间达到负的最大值。如果用它来预报降水量变化, 即表明从26日12:00以后到27日12:00之前, 该位置上的降水量应该是逐渐减小的, 用1次/6 h的观测资料 (图略) 验证, 发现从单点的广义湿位涡倾向值的变化可以很好地预测该点附近区域的降水量变化。图 4b给出的是2003年梅雨锋暴雨个例中33°N, 119°E处广义湿位涡倾向的时间演变, 发现也是在广义湿位涡倾向为负值时对应降水的减小, 广义湿位涡倾向为正值时对应降水的增加, 说明广义湿位涡的异常确实可以作为预报降水的一个动力指标。
|
|
| 图 4. 暴雨中心点不同高度处广义湿位涡倾向的时间演变 (单位:10 -8 PVU·s -1)(a)37°N, 115°E处2001年7月26日06:00—27日18:00, (b)33°N, 119°E处2003年7月7日18:00—9日06:00 Fig 4. The generalized moist potential vorticity tendency evolution of the torrential rain center at 37°N, 115°E from 06:00 on July 26 to 18:00 on July 27, 2001 (a) and at 33°N, 119°E from 18:00 on July 7 to 06:00 on July 9, 2003 (b)(unit:PVU·s -1) | |
单点的广义湿位涡倾向值对未来时次附近区域的强降水变化有较好的指示意义, 那么在整个区域上广义湿位涡倾向的预报性能又怎样呢?以2001年7月27日00:00 850 hPa上广义湿位涡倾向的水平分布 (图略) 为例来分析。在河北南部和江苏北部地区出现明显的正中心, 表明未来时刻广义湿位涡正异常可能加剧, 预示了水汽在该地区有集中, 水汽梯度增大, 有可能发生强降水。而事实上 (图 1a), 27日06:00河北南部到河南北部地区的雨带中心位于河北南部地区, 且中心位置38°N, 115°E对应很好。从江淮暴雨的例子来看 (图略), 整个广义湿位涡异常区域从湖南开始沿西南─东北方向延伸到江苏, 表明这一异常区域的降水会增强, 而实际雨带的分布与整个广义湿位涡倾向的异常分布也是基本对应的。可见, 实际暴雨的发生与消失和从广义湿位涡倾向变化方面作出的判断基本一致。所以, 无论是对单站的强降水趋势预报还是对较大范围区域的降水分布预报, 广义湿位涡倾向都是一个很好的动力示踪物。
从广义湿位涡的定义及其倾向方程可见, 广义湿位涡的异常包含了大气动力、热力及水汽的综合作用, 相对于常用的温度、湿度等物理量来说, 它能在一定程度上综合反映风场、温度场和水汽场的相互作用。因此, 广义湿位涡及其异常变化对暴雨天气的动力识别具有一定的预报意义。但由于目前所用资料分辨率还不够细, 使得这种广义湿位涡大值区还处于一个比较大的范围内。
3 小结通过广义相当位温概念及广义湿位涡方程, 从理论和诊断上论证了利用广义湿位涡异常识别暴雨天气出现的可行性, 并探讨利用广义湿位涡倾向对暴雨天气的发生进行短时预报的可能性。对华北暴雨和江淮梅雨锋暴雨个例的广义湿位涡异常的诊断分析表明, 暴雨发生以及发生前, 均伴有非均匀饱和广义湿位涡的异常。因此, 可以用对流层中低层的广义湿位涡及其异常作为暴雨发生的动力示踪指数之一。但是, 用广义湿位涡倾向异常时会出现对暴雨的空报现象, 除了需进一步对该理论进行补充和完善, 即综合考虑降水产生的凝结加热或辐射冷却作用项以外, 在实际工作中, 将广义湿位涡和广义湿位涡倾向的异常区域与传统环流形势分析、温度、湿度 (尤其是温度、湿度的变化) 的预报相结合, 并加入其他行之有效的暴雨临近预报动力方法[22-23]和各种观测资料[24-25], 将会有助于暴雨预报准确率的提高。
| [1] | Ertel H, Ein neuer hydrodynamischer Erhaltungssatz. Naturwissenschaften, 1942, 30: 543–544. DOI:10.1007/BF01475602 |
| [2] | Robison W A, On the structure of potential vorticity in baroclinic instability. Tellus, 1989, 41A: 275–284. DOI:10.1111/tela.1989.41A.issue-4 |
| [3] | Betts D A, Hoskins B J, Conditional symmetric instability—a possible explanation for frontal rainbands. Quart J Roy Meteor Soc, 1979, 105: 945–962. DOI:10.1002/(ISSN)1477-870X |
| [4] | Betts D A, Sharp J C, The relevance of conditional symmetric instability to the prediction of mesoscale frontal rainbands. Quart J Roy Meteor Soc, 1982, 102: 595–602. |
| [5] | Hoskins B J, Berrisford P, A potential vorticity perspective of the storm of 15—16 October 1987. Weather, 1988, 43: 122–129. DOI:10.1002/wea.1988.43.issue-3 |
| [6] | Davis C A, Emanuel K A, Potential vorticity diagnostics of cyclogensis. Mon Wea Rev, 1991, 119: 1929–1953. DOI:10.1175/1520-0493(1991)119<1929:PVDOC>2.0.CO;2 |
| [7] | Thorpe A J, Diagnosis of balanced vortex structure using potential vorticity. J Atmos Sci, 1985, 42: 397–406. DOI:10.1175/1520-0469(1985)042<0397:DOBVSU>2.0.CO;2 |
| [8] | Montgomery M T, Farrell B F, Tropical cyclone formation. J Atmos Sci, 1993, 50: 285–310. DOI:10.1175/1520-0469(1993)050<0285:TCF>2.0.CO;2 |
| [9] | Hertenstein R F A, Schubert W H, Potential vorticity anomalies associated with squall lines. Mon Wea Rev, 1991, 119: 1663–1672. DOI:10.1175/1520-0493(1991)119<1663:PVAAWS>2.0.CO;2 |
| [10] | Shapiro M A, A multiple structured frontal zone-jet stream system as revealed by meteorologically instrumented aircraft. Mon Wea Rev, 1974, 102: 244–253. DOI:10.1175/1520-0493(1974)102<0244:AMSFZJ>2.0.CO;2 |
| [11] | Shapiro M A, The role of turbulent heat flux in the generation of potential vorticity in the vicinity of upper-level jet stream systems. Mon Wea Rev, 1976, 104: 892–906. DOI:10.1175/1520-0493(1976)104<0892:TROTHF>2.0.CO;2 |
| [12] | Montgomery M T, Farrell B F, Moist surface frontogenesis associated with interior potential vorticity anomalies in a semigeostrophic model. J Atmos Sci, 1991, 48: 343–347. DOI:10.1175/1520-0469(1991)048<0343:MSFAWI>2.0.CO;2 |
| [13] | Chan D S T, Cho H R, Meso-scale potential vorticity anomalies and rainbands.Part Ⅰ:Adiabatic dynamics of potential vorticity anomalies. J Atmos Sci, 1989, 46: 1713–1723. DOI:10.1175/1520-0469(1989)046<1713:MPVAAR>2.0.CO;2 |
| [14] | Xu Q, Formation and evolution of frontal rainbands and geostrophic potential vorticity anomalies. J Atmos Sci, 1992, 49: 629–648. DOI:10.1175/1520-0469(1992)049<0629:FAEOFR>2.0.CO;2 |
| [15] | 高守亭, 雷霆, 周玉淑. 强暴雨系统中湿位涡异常的诊断分析. 应用气象学报, 2002, 13, (6): 663–670. |
| [16] | Gao S, Pin F, Li X, A convective vorticity vector associated with tropical convection:A two-dimensional cloud-resolving modeling study. J Geophys Res, 2004, 109: D14106. DOI:10.1029/2004JD004807 |
| [17] | Gao S T, Li X, Tao W-K, et al. Convective and moist vorticity vectors associated with tropical oceanic convection:A three-dimensional cloud-resolving model simulation. J Geophys Res, 2007, 112: D01105. |
| [18] | Gao S, Cui X, Zhou Y, et al. A modeling study of moist and dynamic vorticity vectors associated with two-dimensional tropical convection. J Geophys Res, 1005, 110: D17104. DOI:10.1029/2004JD005675 |
| [19] | Gao S, Zhou Y, Li X, Effects of diurnal variations on tropical equilibrium states:A two-dimensional cloud-resolving modeling study. J Atmos Sci, 2007, 64, (2): 656–664. DOI:10.1175/JAS3835.1 |
| [20] | Gao S, Wang X, Zhou Y, Generation of generalized moist potential vorticity in a frictionless and moist adiabatic flow. Geophy Res Lett, 2004, 31: L12113. |
| [21] | Gao S, Zhou Y, Lei T, et al. Analyses of hot and humid weather in Beijing city in summer and its dynamical identification. Sci in China (Series D:Earth Sciences), 2005, 48, (Supp Ⅱ): 128–137. |
| [22] | Yang S, Gao S, Wang D. Diagnostic analysis of the ageostrophic Q vector in the non-uniformly saturated, frictionless and moist adiabatic flow. J Geophys Res, 112, No.D9, D09115 10.1029/2006JD007764. |
| [23] | 吴国雄, 蔡雅萍, 唐晓菁. 湿位涡和倾斜涡度发展. 气象学报, 1995, 53, (4): 387–405. |
| [24] | 李柏, 周玉淑, 张沛源. 新一代天气雷达资料在2003年淮河流域暴雨模拟中的初步应用:模拟降水和风场的对比. 大气科学, 2007, 31, (5): 683–692. |
| [25] | 倪允琪, 周秀骥, 张人禾, 等. 我国南方暴雨的试验与研究. 应用气象学报, 2006, 17, (6): 690–704. |
 2007, 18 (6): 754-759
2007, 18 (6): 754-759

