应用气象学报  2007, 18 (6): 748-753   PDF    
引用本文
关敏, 杨忠东. 星载GPS数据及高精度轨道模型在极轨卫星轨道计算中的应用[J]. 应用气象学报, 2007, 18(6): 748-753.
Guan Min, Yang Zhongdong. Application of On-board GPS Data and High-precision Orbit Model to Polar Satellites Orbits Calculation[J]. Journal of Applied Meteorological Science, 2007, 18(6): 748-753  
星载GPS数据及高精度轨道模型在极轨卫星轨道计算中的应用
关敏, 杨忠东     
国家卫星气象中心, 北京 100081
2007-01-10 收到, 2007-02-27 收到修改稿.
摘要: 利用GPS测量的卫星位置数据, 计算出卫星的瞬时位置和速度, 并以此为初值, 用基于数值积分的高精度轨道模型对卫星轨道进行预报。将这种方法分别用于Terra/MODIS和Aqua/MODIS的轨道计算, 并与GPS测量的卫星轨道进行比较。结果表明:由此方法计算出的卫星在某一时刻瞬时速度矢量与GPS测量的卫星速度偏差不超过±0.1 m/s; 再以此为初值计算卫星位置和速度, 与GPS测量值进行比较, 在Terra/MODIS和Aqua/MODIS一条时长约10 min的轨道数据中卫星位置偏差不超过±40 m, 速度偏差不超过±0.2 m/s。因此该方法基本适用于FY-3卫星轨道计算, 且根据数值方法计算结果的连续稳定性, 还可以用于检验GPS测量数据的可靠性。
关键词: 高精度轨道模型    数值积分方法    GPS    
Application of On-board GPS Data and High-precision Orbit Model to Polar Satellites Orbits Calculation
Guan Min, Yang Zhongdong     
National Satellite Meteorological Center, Beijing 100081
Abstract: A high precision orbit model based on numerical integration is introduced. Satellite's instantaneous position and velocity are derived from the position data measured by on-board GPS receiver, and then they are used as initial value to predict the orbit by high precision numerical integration. The six orbital elements which are used to describe the motion of satellite can be transformed to the satellite's position and velocity, and vice versa. The satellite's instantaneous orbital elements at time t1 can be calculated from satellite's two position vectors and at time t2 and t2 respectively, then the satellite's instantaneous position and velocity at time t2 can be obtained. There are many perturbing terms that have been considered in the satellite's high precision orbit model, including the aspherical gravitations of the earth, the perturbations that arise from the gravitational attraction of the sun and the moon, the solar radiation pressure and the atmospheric drag. The earth gravity model that is used is the EGM-96 model of degree and order of 360. Numerical methods are used to solve the equation of the satellite's motion. The variable order and stepsize method DE/DEABM are used for the numerical integration. This new method are applied to Terra/Aqua-MODIS satellite's orbit calculation. Satellite Terra's position vectors r1 at time t1 and r2 at time t2 are used to compute the instantaneous velocity vector. The result shows that the departure between the calculated observation and the GPS measurement is very small with the error of instantaneous speed less than±0.1 m/s. Then they are used as initial input to predict one of Terra/MODIS' further 10-minute orbit by applying the high precision orbit model. It shows that the satellite's position and velocity vectors and range which are predicted by this method are all consistent with the measurements by GPS. The following results are gained that the position error is between-20 m and +5 m, the velocity error is less than±0.2 m/s. The same method are used to compute Aqua/MODIS' orbit. The Aqua's position vectors error between the predictions from high precision orbit model and the GPS measurements is less than 40 m, the error of predicted velocity vectors is less than±0.4 m/s. Because of the high precision and the continuous stability in certain time, the high precision orbit model based on numerical integration can be used to verify the reliability of GPS measurement results if the initial input is correct, and substitute the wrong GPS measurement value. Further more, the new method is suitable for FY-3 satellite's orbit computation.
Key words: high-precision orbit model     numerical integration     GPS    
引言

随着卫星遥感应用的不断深入和遥感图像分辨率的不断提高, 对卫星轨道确定、预报和控制计算精度提出了更高的要求。另外, 由于分析方法中力学模型精化所带来的复杂性, 仍采用纯分析方法求解卫星运动方程已无法满足要求, 于是数值积分方法便成为解决这一问题的主要途径。描述卫星轨道运动的微分方程相当复杂, 除二体问题等少数几种情况外, 都不可能给出严格解, 即使在一定条件下设定为受摄二体问题, 比如卫星在轨运动, 运动方程转化为小参数方程, 可以给出相应的小参数幂级数解, 但要满足高精度要求, 就涉及到幂级数的高阶项, 其项数之多, 即使具体推导出相应的表达式也难以采用, 甚至有的力学因素无法用简单的分析表达式写出。这就促使求解微分方程的数值方法在卫星轨道力学计算应用中越来越重要, 特别是在当今计算机技术迅猛发展的时代, 更加显示出它的优越性[1-2]。

大多数极轨太阳同步环境气象卫星, 如NOAA/AVHRR 3, Terra/MODIS, Aqua/MODIS和LandSat-7/TM等的地理定位和导航软件所应用的轨道模型 (假设条件) 都略有不同, 所以在算法上也不尽一致。NOAA/AVHRR 3基于传统分析方法建立轨道模型, 在遥感图像地理定位中加入卫星姿态模型, 以提高遥感图像地理定位的精度[3-4]。Terra/MODIS和Aqua/MODIS则依靠星载GPS测量卫星的实时位置和速度, 陀螺仪和星敏感器测量卫星的实时姿态, 用于遥感数据地理定位[5]。本文介绍的卫星轨道模型是一种基于数值积分的高精度轨道模型, 在只有卫星瞬时位置数据的前提下, 通过算法得到卫星的实时速度, 进而完成遥感图像地理定位, 以及一定时段内卫星高精度轨道预报。

1 GPS定位数据确定卫星初轨

描述卫星运动的6个独立的轨道根数与卫星位置、速度向量之间可以互相换算。已知卫星t1时刻位置矢量r1和t2时刻位置r2, 计算卫星在t1时刻瞬时轨道根数的算法如下[6]。

计算卫星轨道倾角i和升交点赤经Ω:

(1)
(2)
(3)

计算半通径p:

(4)

上式中, h为面积速度, GM⊕为地心引力常数。

计算偏心率e、真近点角υ和近地点经度ω:

(5)
(6)

其中r0为r2垂直于r1的分量。

(7)
(8)

计算卫星轨道半长轴a和平近点角M:

(9)
(10)
(11)

由式 (1)~(11) 可以得到卫星的6个轨道根数, 当然ω, Ω和E的计算还存在判象限的问题[1-2]。进一步, 可以计算卫星在t1时刻的瞬时位置和速度[6]。

(12)
(13)

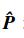
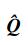
其中, 和分别表示近地点和半通径方向的单位向量。

最后将r, 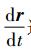通过坐标旋转得到在相应坐标系中表达式[7]。

2 高精度数值积分轨道模型

卫星高精度轨道模型考虑了多项摄动因素, 首先是地球的非球形引力项, 使用了高精度高阶EGM-96地球引力场模型, 提高了非球形引力摄动计算精度, 其次还考虑了太阳、月亮引力项, 辐射光压摄动和大气摄动因素①。

①杨忠东, 许健民, 关敏, 等.气象卫星对地观测数据综合处理原型系统技术报告.2005.

对于低轨卫星而言, 它的受力情况最主要是地球非球形引力势, 可以表示为[6]

(14)

式 (14) 中, R⊕为地球赤道半径; r, λ, φ分别为卫星矢径和经、纬度; Pnm为n次m阶缔合勒让德多项式; Cnm和Snm是n次m阶谐系数。式 (14) 中包括了地球引力的主要部分, 是地球质量全部集中于地心的质点引力位; 以及真实地球引力位对假设质点地球引力位的修正部分, 包括带谐项和田谐项两部分, 它们反映了地球形状不规则性和密度分布不均匀性, 相应的Cnm和Snm是上述不均匀性和不规则性程度的具体度量。

要得到系数Cnm和Snm的准确值, 需要高精度的地球引力场模型。卫星高精度轨道模型使用了EGM-96地球引力场模型。EGM-96是利用联合测量数据确定的全球重力场模型, 它的位系数取到360阶, 是目前世界上位系数阶数最高的全球重力场模型[6]。

此外, 卫星高精度轨道模型中还考虑了大气阻力摄动、日月引力摄动以及辐射光压摄动。

采用数值方法求解由上述摄动项组成右函数的卫星运动方程。数值积分采用变阶变步长DE/DEABM方法[6]。

3 基于GPS数据和高精度轨道模型的卫星轨道计算流程

利用GPS测量卫星的t1时刻位置矢量r1和t2时刻位置r2, 计算出卫星在t1时刻的瞬时和瞬时速度v1, 再以r1和v1为初值, 用卫星轨道数值积分计算模型DE/DEABM数值方法对卫星的轨道进行预报。实现流程如图 1所示。

图 1. 基于GPS数据和高精度轨道模型的卫星轨道计算流程 Fig 1. Flow chart of satellite orbit calculation based GPS data and high precision orbit model

4 星载GPS卫星轨道计算实例

以北京地面站收取的Terra/MODIS 2006年3月12日01:39(世界时, 下同) 的一条轨道为例, 提取定位数据文件中GPS测量的卫星位置、速度数据以及相应的时间。由GPS测量Terra卫星的t1时刻位置矢量r1和t2时刻位置r2, 计算出Terra卫星在t2时刻瞬时速度v 1与GPS实测值的偏差小于±0.1 m/s。再以此为初值, 用高精度数值积分轨道模型对卫星的轨道进行预报, 积分步长为1.47714 s, 这是Terra/MODIS的扫描周期。结果表明, 以此方法计算出的卫星位置、速度矢量各分量都与GPS的实测值非常一致, 卫星矢径也与GPS实测值一致。如图 2所示, 计算得出的卫星位置矢量各分量以及卫星矢径与GPS实测值的偏差在-20~+5 m之间。图中的横坐标是自1993年1月1日00:00:00开始的秒计数 (国际原子时), 以下所有图中的横坐标亦然, 不再赘述。图 3给出了卫星速度矢量各分量的偏差, 可以看出, 在该条轨道中, 计算得出的卫星速度与GPS实测结果的偏差在-0.2~+0.2 m/s之间。

图 2. 轨道模型计算的Terra卫星位置与GPS实测值的偏差 (a) 卫星位置, (b) 卫星矢径 Fig 2. The error of Terra's position between calculated method and the real measurement (a) position, (b) radius vector

图 3. 轨道模型计算的Terra卫星速度与GPS实测值的偏差 Fig 3. The error of Terra's velocity between calculated method and the real measurement

图 2中有一明显的跳变点, 经分析, 这是GPS测量值错误导致的。表 1中所示为Terra/MODIS 2006年3月12日01:39的卫星定位数据中GPS测量数据的节选, 其中有对应于图 2中跳变点的GPS实测数据。可以看出GPS测量数据随时间的变化是有规律的, 随时间近似等差递增或递减。而图 2中跳变点对应的GPS测量值是不符合这种变化规律的, 所以认定该时刻GPS测量数据错误。

表 1 GPS测量数据分析 Table 1 Analysis of GPS measurement data

由于基于数值方法的卫星轨道外推计算结果在一定时间段内精度很高, 且连续, 所以只要确保数值积分的初值正确, 那么基于数值方法的高精度轨道模型外推计算的结果可以用来检验GPS测量数据的质量, 并且替换错误的GPS测量值。

用同样的方法对北京地面站收取的Aqua卫星2006年3月12日04:54的轨道数据进行计算。计算出的Aqua卫星在t1时刻瞬时速度v1与GPS实测值的偏差不超过±0.1 m/s。在该条轨道中, 使用高精度卫星轨道模型计算的Aqua卫星位置向量各分量与GPS测量值的偏差在-40~+10 m之间, 卫星矢径的偏差小于35 m。使用轨道模型计算的Aqua卫星速度向量各分量与GPS测量值的偏差小于±0.4 m/s。

5 小结

通过实例计算分析与比较, 可以看出由GPS测量两组位置数据计算出的卫星速度, 与GPS实测的卫星速度偏差非常小, 再通过基于数值积分的高精度轨道模型, 外推计算的卫星位置、速度矢量与GPS实测数据在一定时间段内符合程度非常好, 两者在同一时刻的最大位置偏差不超过±40 m。

我国下一代极轨气象卫星FY-3将搭载高动态GPS接收机, 可以实时提供卫星的三维位置信息。根据地面应用系统需求, 要使用两组以上卫星的位置通过算法得到卫星的实时速度, 进而完成遥感图像地理定位, 以及卫星的精密定轨和高精度轨道预报。对于FY-3卫星则可以采用这种方法得到卫星瞬时位置、速度向量, 并做一定时间段内的轨道预报。同时, 由于数值方法计算结果的高精度和连续性, 还可以将此用于检验GPS测量数据的可靠性, 替代错误的GPS测量数据。

在这种方法中, 基于数值积分的高精度轨道模型的初值是GPS测量的卫星瞬时位置和由算法得到的卫星瞬时速度, 这只是卫星的初轨, 要确定卫星的精密轨道, 还需要卫星轨道较长弧段上的多次实测值, 进行轨道改进后才能得到卫星的精密轨道。由此, 轨道根数就能通过高精度数值积分轨道模型对卫星轨道做较长时间的准确预报。

另外, 为保证高精度数值积分轨道模型计算结果的准确性, 必须保证初值的正确, 这要求作为初值的GPS测量值正确, 所以还需要首先检验GPS测量值的质量。

参考文献
[1] 刘林. 天体力学方法. 南京: 南京大学出版社, 1998.
[2] 刘林. 人造地球卫星轨道力学. 北京: 高等教育出版社, 1992.
[3] George W R, Daniel G B, William J E, Precise AVHRR image navigation. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32, (3): 644–657. DOI:10.1109/36.297982
[4] Emery W, Ikeda M, AVHRR image navigation:Summary and review. Canadian Journal of Remote Sensing, 1989, 10: 46–56.
[5] Robert E W, Masahiro N, Albert J F, et al. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sens Environ, 2002, 83: 31–49. DOI:10.1016/S0034-4257(02)00085-8
[6] Oliver Montenbruck, Eberhard Gill, Satellite Orbits. Berlin: Springer-Verlag, Germany, 2000.
[7] Nisihama M, Wolfe R, Fleig A, et al. MODIS Geolocation Algorithm and Error Analysis Tools. Geoscience and Remote Sensing Symposium Proceedings, 2000, 5: 2053–2055.