气候条件是农作物生长和获得高产的重要因素, 气候区划则是农业生产的重要内容之一。气候区划就是把气候条件相似的区域划分为同一个分区, 以便调整种植结构, 因地制宜地发展农业生产。比如, 魏丽等取得的贵溪市优质双季稻适宜播种期等7种作物的气候区划研究成果已在贵溪市政府制定农业产业结构和发展规划中得到应用[1]; 郭文利等开展的优质板栗种植区划工作为北京地区优质板栗的推广种植提供了参考依据[2]。因此, 合理的气候区划对指导农业生产实践具有重要意义。
气候区划是典型的多因素影响下复杂的非线性分类问题, 其方法与模型的研究也备受关注。多元统计学的发展, 为气候区划提供了先进的数学工具, 常用的方法有聚类分析、判别分析、主分量分析、因子分析、典型相关分析及模糊聚类等等[3], 文献[4]采用统计聚类和旋转主分量分析相结合的方法对我国年最高 (低) 气温的年际变化型态进行了地理区划, 文献[5-7]则运用多元统计分析中的系统聚类方法实现了气候区划分析和影响苹果品质的气象因素的识别, 模糊聚类分析方法也被成功运用于黔西北林木气候区划[8]。然而, 目前还没有统一公认的气候区划模型和方法, 气候区划方法还需要在以下两方面予以完善:一方面, 如何最充分地挖掘气候区划指标数据信息, 将气候区划多因素问题进行降维处理, 比如将其转化到线性空间或二维, 以便更好地利用成熟的常规方法解决气候区划问题。另一方面, 减少或消除人为干扰, 更多或完全依据指标数据结构特性进行气候区划, 以得到更为客观的区划结果, 而目前的一些方法在分析过程中需要根据经验确定指标权重, 具有一定的随意性。针对上述问题并结合气候区划的特点, 本文以投影寻踪理论为基础结合动态聚类思想建立了一种气候区划模型, 即基于投影寻踪原理的动态聚类 (Dynamic Cluster Based on Projection Pursuit) 模型, 本文将在详细介绍基于投影寻踪原理的动态聚类模型建立的基础上, 结合个例分析具体阐述气候区划的基于投影寻踪原理的动态聚类模型。
1 基于投影寻踪原理的动态聚类模型投影寻踪就是将高维数据向低维空间投影, 通过分析低维空间的投影特性来研究高维数据特征, 是处理多因素复杂问题的一种统计方法[9]。依据投影寻踪思想建立的投影寻踪聚类模型已在多因素评价、聚类、优选等方面得到了广泛应用[10-18], 充分体现了投影寻踪在处理高维数据方面的优势。然而, 在投影寻踪聚类模型中的唯一参数———密度窗宽的取值还主要是依靠经验或试算来确定[9, 16], 缺乏理论依据。针对这一问题, 引入动态聚类思想[19], 以动态聚类思想构建投影指标, 对投影寻踪聚类模型进行改进, 进而建立基于投影寻踪的动态聚类模型。
若第i个样本第j个指标为xij0(i=1, …, n; j=1, …, m; n为样本个数, m为指标个数), 则建立基于投影寻踪原理动态聚类模型的步骤如下:
①数据无量纲化。由于各评价指标的量纲不尽相同, 为了消除量纲效应, 在建模之前对各指标数据进行无量纲化处理, 无量纲化公式为
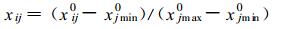
|
(1) |
式 (1) 中, xjmax0和xjmin0分别为第j个指标的样本最大值和最小值。
②线性投影。所谓投影实质上就是从不同的角度去观察数据, 寻找能够最大程度地反映数据特征和最能充分挖掘数据信息的最佳观察角度即最优投影方向。将高维数据信息通过投影方法转化到低维空间, 不但形象直观, 而且便于运用常规的方法进行高维数据分析处理。这里选用线性投影, 即将高维数据投影到一维线性空间进行研究, 设a为m维单位投影方向向量, 其分量为a1, a2 …, am, 则xij的一维投影特征值zi可用式 (2) 描述, 即
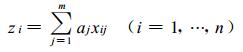
|
(2) |
并定义z=(z1, z2, …zi, …, zn) 为投影特征值集合。
③构造投影指标。这是基于投影寻踪原理的动态聚类模型建立的关键, 是高维数据向低维空间投影所遵循的规则, 是寻找最优投影方向的依据, 因此, 只有构造合理的投影指标才能获得科学的聚类结果。本文依据动态聚类思想来构造投影指标[19]。
首先, 设s(zi, zk) 为任意两投影特征值间的绝对值距离, 即s(zi, zk)=zi-zk, k=1, …, n; 将待聚类样本分为N(2≤N < n) 类, 用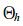
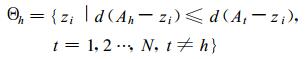
|
(3) |
其中d (Ah-zi)=|zi-Ah|, d(At-zi)=|zi-At|, Ah和At分别为第h类和第t类的初始聚核, 在实际操作过程可用所得到的分类样本投影特征值的均值迭代替换, 具体可参阅文献[19]。
其次, 类同样本的邻近程度用类同聚集度dd(a) 表示为
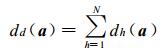
|
(4) |
其中
样本间的离散程度用类异分散度表示为
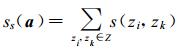
|
(5) |
ss(a) 愈大则样本离散程度越高。
最后, 根据动态聚类构建的投影指标可表示为
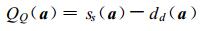
|
(6) |
显然, ss(a) 越大表示样本间的距离越远, 即类异样本之间分散越开; 相反, dd(a) 越小表示类同样本之间的距离越近, 即表示同类样本之间越集中。因此, 当QQ(a) 取得最大值时, 就同时实现了类异样本尽量散开、类同样本尽量集中的聚类目的。
④模型及优化。当式 (6) 取得最大值时便可以得到最能反映数据特征的最优投影方向和聚类结果。因此, 基于投影寻踪原理的动态聚类模型可以描述为式 (7) 所示的非线性优化问题。
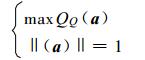
|
(7) |
本文采用遗传算法求解[10, 17], 具体过程包括5个步骤。第1步, 随机产生p(建议p≥300) 组m维单位投影方向向量a(即生成父代群体), 按式 (2) 分别计算得到p组投影特征值向量z; 第2步, 依据z分别计算ss(a) 和dd(a), 进而根据式 (6) 计算得到p个投影指标QQ(a); 第3步, 以QQ(a) 进行适应度评价, QQ(a) 值越大则个体适应度越高, 并通过遗传算法规则中的选择、交叉和变异操作分别生成第1子代、第2子代和第3子代群体, 得到相应的新的投影方向向量; 第4步, 分别计算第1子代、第2子代和第3子代投影方向向量所对应的QQ(a), 并按从大到小的顺序进行排序, 根据QQ(a) 值越大越优的原则, 选择前p组作为新的投影方向向量 (若不足p组则通过随机生成的方法补足p组), 回到第1步; 第5步, 当前后两代投影指标QQ(a) 的差值满足给定要求时停止计算, 输出最后的聚类结果和最优投影方向向量。
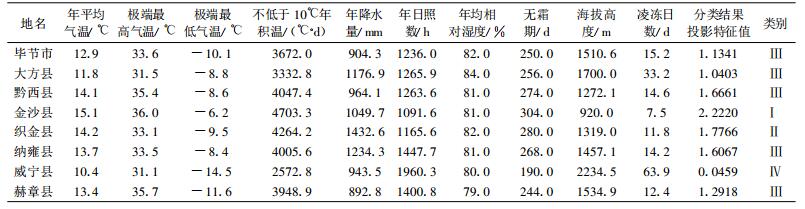
2 实例分析为了验证基于投影寻踪原理的动态聚类模型的有效性并阐述其运算过程, 选用黔西北地区气候区划进行案例分析[8]。黔西北地区地处贵州省西北部, 103°36′~106°43′E, 20°31′~27°46′N, 全区辖毕节市、大方县、黔西县、金沙县、织金县、纳雍县、威宁彝族回族苗族自治县和赫章县等行政区划。该地区全年云雾多, 日照少, 气温年变化小, 日温差大, 具有高原气候特色, 有利于多种森林植物的生长, 合理进行该地区的气候区划, 有利于调整林种结构, 促进该地区林木产业。选择与林木生长关系密切的10个影响因子构建气候区划指标体系, 即①年平均气温, ②极端最高气温, ③极端最低气温, ④不低于10℃年积温, ⑤年降水量, ⑥年日照时数, ⑦年均相对湿度, ⑧无霜期, ⑨海拔高度, ⑩凌冻日数。表 1给出了评价指标值。
|
|
表 1 评价指标值及结果 Table 1 Index value and results |
首先, 确定样本聚类数。这里将样本分为4类, 即N=4。
其次, 依据表 1的样本指标值建立气候区划的基于投影寻踪原理的动态聚类模型, 其中n=8, m=10。通过基于投影寻踪原理的动态聚类模型运算得最优投影方向向量为dd (a)=(0.4688, 0.3972, 0.4294, 0.4263, 0.3054, 0.0013, 0.0209, 0.4032, 0.0048, 0.0070), 同时表 1中还列出各市、县的投影特征值以及模型分类输出结果。
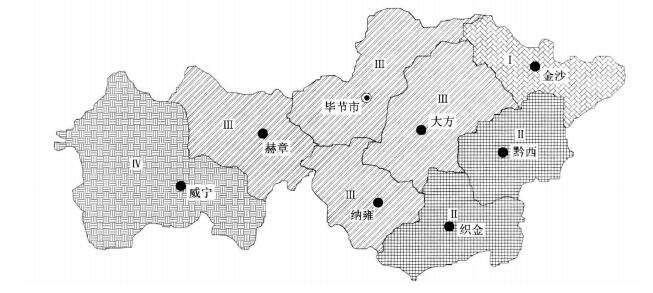
最后, 基于投影寻踪原理的动态聚类模型输出的聚类结果为, 金沙县和威宁县可划分为不同的两个气候分区, 黔西县和织金县属于同一个气候分区, 毕节市、大方县、纳雍县和赫章县又属于另一个气候分区。这一分析结果与文献[8]和文献[20]的分类结果完全一致, 同时也与黔西北地区的地理分布相吻合, 即金沙县处于该地区东部高原温和湿润气候区, 威宁县属于西部高原 (高中山) 温凉湿润区, 其余属于中部中山温暖湿润区, 图 1给出了毕节地区气候区划行政示意图。应当指出, 基于投影寻踪原理的动态聚类模型完全根据样本数据特性进行样本聚类, 避免了依据专家知识确定指标权重对区划结果的人为影响, 因此可以得到较合理的气候区划结果。另一方面, 基于投影寻踪原理的动态聚类模型不仅发挥了投影寻踪理论在处理复杂多因素气候区划问题上的优势, 同时融入了动态聚类的思想, 具有分类结果客观明确、便于操作应用的优点。
|
|
| 图 1. 毕节地区气候区划示意图 Fig 1. Scheme of climate division in Bijie | |
3 结论
基于投影寻踪的动态聚类模型是投影寻踪和动态聚类的有机结合, 充分发挥了投影寻踪处理高维数据的突出优势, 完全根据数据自身特性进行样本聚类分析, 具有操作简便、稳定性好、客观性强及分类结果明确等特点, 为多因素聚类分析问题的解决开辟了一条新途径。实际应用表明, 基于投影寻踪原理的动态聚类模型在气候区划应用中取得了良好的效果, 是气候区划分析的一种新方法。
| [1] | 魏丽, 殷剑敏, 黄淑娥, 等. 贵溪市植被资源遥感调查和综合气候区划. 应用气象学报, 2003, 14, (6): 715–721. |
| [2] | 郭文利, 王志华, 赵新平, 等. 北京地区优质板栗细网格农业气候区划. 应用气象学报, 2004, 15, (3): 382–384. |
| [3] | 么枕生, 丁裕国. 气候统计. 北京: 气象出版社, 1990: 477-522. |
| [4] | 刘吉峰, 李世杰, 丁裕国, 等. 一种用于中国年最高 (低) 气温区划的新的聚类方法. 高原气象, 2005, 24, (6): 966–973. |
| [5] | 闫静, 简慰民, 周有芬, 等. 中国草坪气候区划探讨. 南京气象学院学报, 1998, 21, (3): 370–376. |
| [6] | 刘振中, 徐梅. 三江平原地区农业气候区划的数学方法. 农业系统科学与综合研究, 1997, 13, (1): 49–50;55. |
| [7] | 魏钦平, 张继祥, 毛志泉, 等. 苹果优质生产的最适气象因子和气候区划. 应用生态学报, 2003, 14, (5): 713–716. |
| [8] | 刘崇欣. 黔西北林木气候区划的聚类分析. 农业系统科学与综合研究, 1997, 13, (3): 231–233;228. |
| [9] | Friedman J H, Tukey J W, A projection pursuit algorithm for exploratory data analysis. IEEE Trans on computer, 1974, C-23, (9): 881–890. DOI:10.1109/T-C.1974.224051 |
| [10] | 张欣莉, 丁晶, 李祚泳, 等. 投影寻踪新算法在水质评价模型中的应用. 中国环境科学, 2000, 20, (2): 187–189. |
| [11] | 张欣莉, 任仕泉, 罗利. 企业竞争力评价的投影寻踪模型. 数理统计与管理, 2005, 24, (4): 53–55;117. |
| [12] | 金菊良, 张欣莉, 丁晶. 评估洪水灾情等级的投影寻踪模型. 系统工程理论与实践, 2002, 22, (2): 140–144. |
| [13] | 金菊良, 张礼兵, 潘金锋. 基于投影寻踪的天然草地分类模型. 生态学报, 2003, 23, (10): 2184–2188. |
| [14] | 黄晓荣, 梁川, 付强, 等. 基于RAGA的PPC模型对区域水资源可持续利用的评价. 四川大学学报 (工程科学版), 2003, 35, (4): 29–32. |
| [15] | 王顺久, 侯玉, 张欣莉, 等. 流域水资源承载能力的综合评价方法. 水利学报, 2003, 34, (1): 88–92. |
| [16] | Wang Shunjiu, Zhang Xinli, Yang Zhifeng, et al. Projection pursuit cluster model based on genetic algorithm and its application in karstic water pollution evaluation. Int J Environ Pollut, 2006, 28, (3-4): 253–260. |
| [17] | 王顺久, 杨志峰, 丁晶. 关中平原地下水资源承载力综合评价的投影寻踪方法. 资源科学, 2004, 26, (6): 104–110. |
| [18] | Wang Shunjiu, Yang Zhifeng, Ding Jing, Projection pursuit cluster model and its application in water quality assessment. J Environ Sci, 2004, 16, (6): 994–995. |
| [19] | 任若恩, 王惠文. 多元统计数据分析-理论、方法、实例. 北京: 国防工业出版社, 2000: 148-151. |
| [20] | 金菊良, 丁晶. 水资源系统工程. 成都: 四川科学技术出版社, 2002: 166-167. |
 2007, 18 (5): 722-726
2007, 18 (5): 722-726