2. 西安电子科技大学, 西安 710077
2. Xidian University, Xi'an 710077
基于数据的机器学习是现代智能技术中十分重要的领域, 主要研究如何从一些观测数据 (样本) 出发得出目前尚不能通过原理分析得到的规律, 利用这些规律去分析客观对象, 对未来的数据或无法观测的数据进行预测[1]。这个过程正是天气预报行业的特色。机器学习主要研究知识获取问题, 在一定程度上克服了20世纪80年代中期就在气象预报中得到广泛应用的专家系统存在的自学习能力差[2]、不能很好地解决知识获取的缺点。
由于Vapnik对统计学习理论 (SLT:Statistical Learning Theory) [3-4]的巨大贡献, 使得基于核方法的机器学习有了很大的发展。支持向量机 (SVM:Support Vector Machine) [3, 5]与支持向量数据描述 (SVDD:Support Vector Data Description) [6]就是其中两个重要的方法。SLT中结构风险最小化理论保证了它们都成为具有良好推广能力的有限样本分类方法[3]。在我国SVM方法2002年被陈永义引入气象领域后[7], 迅速在许多省得到应用和研究[8-11]。而更加新颖的SVDD方法还未被气象科技工作者所接受。气象预报业务中常常遇到两类对立的天气现象出现概率非常不平衡的情况, 以精度最大化为目标的传统机器学习方法容易训练出把所有实例都判断为极高概率类别 (多数类) 的平庸的分类器。SVDD方法是从SVM演变而来的单分类算法。因为主要依靠一类数据进行分类器训练, 从根本上避免了训练数据类别不平衡的影响, 使得它在处理许多气象问题时具有比SVM更明显的优越性。
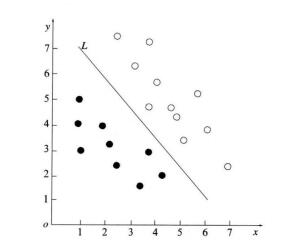
1 SVM理论对于所有样本点构成的训练集合: S={ (x1, y 1), (x2, y2), …, (xm, ym)}, xk∈RN(1≤k≤m) 是以向量形式表示的训练样本, yk ∈{-1,1}为xk的类别。把样本表示为欧氏空间中的点。不失一般性, 只考虑两类问题的情况, 那么所有点用“实心点”和“空心点”两类表示。如图 1所示, SVM的基本思想是, 如果能找到一个可以正确分类样本点的最佳超平面L, 那么对于任意未知类别的点, 就可以依据超平面L预测其类别。可见, SVM方法的实质就是构造合理的划分超平面。实际应用中的绝大部分问题都不会如图 1所示的那样是线性可分的, 特别是对于复杂的未来天气的预测更是如此, 在这些问题中样本空间根本不存在线性的分类超平面。SVM通过借助非线性映射把样本映射到高维的“特征空间”, 在这个空间中寻找出分类超平面。设划分超平面的方程是w·x+b=0, 其中w和b是方程的系数。通常不能满足于仅仅找到一个可以划分训练样本的超平面, 而是应该找到一个最优的划分超平面。最优的标准是不仅可以划分训练样本, 还应该有良好的推广能力, 即对未知样本同样有很好的分类效果。而且后者往往更重要。SVM方法的核心就是求解最优划分超平面。最优划分超平面的标准可以形象的理解为使得其满足S中两类样本点中最近点的距离最大。有关SVM更为详细的介绍请参阅文献[7]。
|
|
| 图 1. SVM的分类面 Fig 1. Classification surface of SVM | |
2 SVDD理论
机器学习中传统的分类方法都是基于区分的, 需要依靠来自不同类别训练样本的强力“支持”。近10年出现了一些基于识别的特殊类型的分类方法, 这些方法也称作“野点侦测”或“数据域描述”[12]。该方法的目标是准确地描述一类样本 (目标样本), 而将人们不关注的类别 (也被称作“野点”) 排除在外[13]。从这些目标类训练样本中“学习”出目标类的“描述”, 再依据这个描述对未知样本是否属于目标类进行判断[14-15]。荷兰代夫特科技大学Tax等人根据这类方法, 在支持向量机的启发下, 提出了支持向量数据描述[6]。因为SVDD可以只使用一类样本, 所以也称为单分类方法。
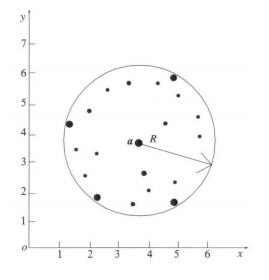
SVDD试图寻找一个封闭的超球面来包围目标集[8]。如图 2所示, 只有落入超球面以内的样本才属于目标类。寻找最优超球面的标准是在包围所有训练目标类的情况下使球的体积尽可能最小[12, 14]。
|
|
| 图 2. SVDD的分类面 Fig 2. Classification surface of SVDD | |
设SVDD寻找的包围目标类的超球面由球心和半径R决定。参照文献[3]中的结构风险最小化 (SRM) 定义, 最优超球面的求解可转化为式 (1) 描述的二次优化问题, 最小值为
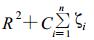
|
(1) |
约束条件为‖xi-a‖2≤R2+ζi, ζi≥0, i=1, 2, …, n
式 (1) 中, xi是目标类的训练实例, 共有n个。松驰变量ζ和惩罚系数C是为提高方法鲁棒性而引入的参数。必须优化自由参数R, a及ζ, 考虑约束条件, 参照文献[3]、[7]中描述SVM的方法, 为优化问题引入Lagrange乘子αi和γ i, 构造出如下Lagrange函数:
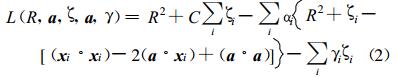
|
(2) |
Lagrange乘子α i≥0, γ i≥0, (x·x) 代表内积。对于每一个样本xi定义了相应的ai和γ i。L需要针对R, a及ζ最小化, 且针对x和γ最大化。令L分别对R, a及ζ取偏导为0, 得到了下面的3个约束:
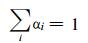
|
(3) |
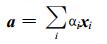
|
(4) |
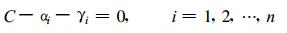
|
(5) |
最后一个约束, 可以进一步写为:
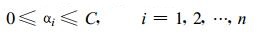
|
(6) |
这样式 (2) 就可以表示为下面的优化问题:
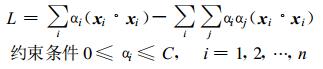
|
(7) |
式 (7) 是一个标准的二次优化问题, 数学上已经有了比较多的解决方法, 解这个优化问题可以得到最优解α。
求得的α是一个n维数向量, αi >0的样本可能在边界上或者在边界外, 则对应xi为支持向量。所以α也被称作支持向量系数。利用它们可以确定球心α和半径R, 进而实现对未知样本的预测。设x为预测样本向量, 则满足该问题的判决函数式 (8) 的样本即可被判别为目标类, 否则属于非目标类。
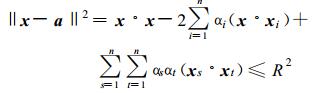
|
(8) |
为了对预测样本有更强的泛化能力, 在判别函数中可以取xi到“球心” a的距离R为支持向量集合中所有xi到球心的平均值, 即式 (9)。VS为支持向量集合, VS的大小为N。
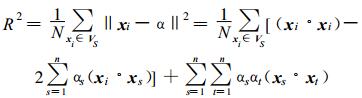
|
(9) |
当然也可使用特征映射ϕ把样本空间映射到高维的特征空间, 并使用Mercer核函数代替映射及内积运算, 从而简化算法。这些方法都是和SVM非常类似的。
3 SVM与SVDD方法的比较和其他机器学习的分类方法一样, SVM在训练模型时需要两类数据。划分超平面的确定依靠分别位于超平面两侧附近的支持向量样本[7]。在样本中不同类别出现的概率大致相当时, 是没有问题的, 但当它们的概率严重不等时, 就显得很不明智。如果由于某种原因某一边样本不能提供很好的“支持”, 则分类面就会严重偏离。其中可能的一个原因就是某一类的实例很少, 即不平衡类别问题。比如天气预报中, 暴雨、冰雹等灾害性天气出现的概率就非常小。由此得到的训练数据中, 无灾害天气的样本远远多于有灾害天气的样本。稀少的灾害天气样本不足以提供对划分超平面足够的支持, 导致分类面过于靠近少数类别, 不能准确地反应客观现实。如果用传统的SVM方法来处理气象中的这类不平衡问题, 势必造成结果严重向多数类别倾斜, 极易对重大的灾害天气漏报。
SVDD方法是一种单分方法, 主要关注目标类别的特点, 在预测时只是判别样本是否属于目标类。因而不存在两类样本的不平衡问题, 预测结果也不应该向多数类倾斜。虽然SVDD主要依靠一类样本训练模型, 但是理论上对于两分类的情况下, 正类和反类都应该可以作为目标类。目标类的错误有两种:错误的接受和错误的拒绝, 前者指非目标类被分为目标类; 后者指目标类被分为非目标类。SVM选择分类边界的原则是使两种错误都较小。SVDD不能确定训练实例的错误接受, 只能最小化错误拒绝。SVDD对于不平衡类别问题的意义是, 如果来自边界一侧实例样本的支持不可靠, 那么就主要依靠可以提供很好支持的那类实例样本确定分类面。因此在实际中, 如果SVDD方法用一类目标预测效果不好时, 可以试图改变目标类, 以期改善预测能力。在两类样本都可用时, 为了能够更加准确地刻画出划分超球面, 选择数量过少的类别作为目标类, 往往会有一定风险: SVM两分类时的分类边界由两类实例的支持向量, 从两侧来“支持”; 而单分类却仅仅依靠包围在内部的目标类的支持向量决定超球面, 所以目标类的可靠“支持”非常重要。
4 暴雨预报的对比试验暴雨是陕西省铜川市盛夏主要的气象灾害之一, 它的发生与气象要素、物理量预报因子有复杂的非线性关系, 是一种小概率事件, 即不平衡类别问题。这既是传统预报方法难以解决的, 又是预报员最难以预报的天气。本章以暴雨为预报对象, 分别用SVM与SVDD方法进行对比预测试验。
4.1 整理资料及分型历史预报因子资料是从1980—2002年共23年7—8月兰州、西安等20个高空站的850, 700, 500 hPa 08:00(北京时, 下同) 要素中选取。根据铜川市站点较少、只有3站的实际情况, 规定3站中至少有1站20:00—次日20:00日降水超过38 mm为一个暴雨个例日, 23年间共有27个暴雨个例。
根据有关资料, 并普查了历史个例天气图, 发现影响铜川暴雨的主要高空天气系统有西南气流及西风槽、台风或热带气旋、副热带高压、切变低涡等, 其中西南气流与西风槽类出现的次数最多, 占所有个例的54%。根据天气学方法, 结合预报员实际预报经验, 寻找了各类型的入型指标, 将历史资料和历史个例按照500 hPa主要影响系统分为4种类型, 即西南气流及西风槽类、台风影响类、副热带高压控制类、低涡切变类。由于西南气流型暴雨个例较多, 最具有代表性, 其入型条件:
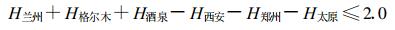
|
(10) |
其中H xx表示xx城市500 hPa的高度。入型条件判别以后, 除这种类型所有暴雨个例进入以外, 还进入了大量的非暴雨个例, 根据预报经验, 又选取了5个判断因子, 当以上个例的资料符合5个因子的任意一个, 就直接判断没有暴雨, 经过筛选过滤以后, 27个暴雨个例全部保留下来, 而把大量无暴雨的个例剔除出去了, 最后总共还有94个预报样本。
4.2 预报因子的选取在这94个样本中, 又根据因子组合、单因子分类、点聚图等方法, 挑选了6个与铜川盛夏西南气流型暴雨发生非常密切且物理意义比较清晰的因子:西安与武汉500 hPa高度差、平凉500 hPa 24 h变温、平凉700 hPa温度露点差24 h变化、酒泉与西安500 hPa温度差、甘孜500 hPa偏南风分量、格尔木500 hPa 24 h变高。
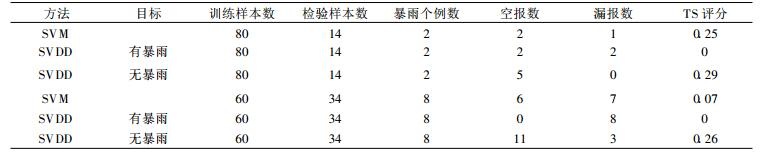
4.3 试验及结果为了能够较准确地检验算法, 先将94组数据分为两部分:模型训练80个, 预测试验14个 (包括2个暴雨样本); 后又重新分配94组数据:模型训练60个, 预测试验34个 (包括8个暴雨样本)。
SVM方法采用Steve Gunn编写的Matlab Support Vector Machine Toolbox (Version 2.1)。SVM的核函数采用径向基函数。算法的参数惩罚系数C和核函数参数σ分别取算法本身的默认值 (分别是无穷大和1)。SVDD使用Tax提供的Data Description Matlab Toolbox (version 0.9)。用SVDD方法时, 目标类选有暴雨和无暴雨两个类别分别进行试验。预报试验结果如表 1。
|
|
表 1 两种方法的预报试验结果1 Table 1 The first results of two prediction methods |
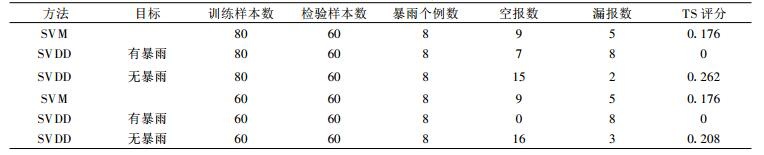
为了进一步检验方法和训练得到的模型的推广能力, 收集2003—2005年6—9月铜川的暴雨数据, 消空后整理出60个数据, 其中包括8个暴雨个例。用第1次试验训练出的模型对新整理出的这60个数据做对比预测试验, 结果如表 2。
|
|
表 2 两种方法的预报试验结果2 Table 2 The second results of two prediction methods |
5 结果分析
用TS评分作为评估性能的指标。从两次试验的结果来看, SVM方法都明显地偏向于无暴雨 (多数类), 漏报比较多。SVDD方法以有暴雨作为目标时, 效果都很不理想; 改变目标后, 空报数目增多, 但漏报数目明显减少, TS评分都好于SVM, 比较符合预报业务的实际情况。分析参与训练的数据, 第1组有暴雨样本25个, 第2组17个, 的确过于稀少, 因而将其作为目标类时, 预测失败了。SVM与SVDD两个方法试验结果的差异完全与两种理论本身的差异一致。由此可见:首先, 在处理类似暴雨预报等气象领域内的不平衡问题时, SVDD是比传统的SVM方法更合适的选择; 其次, 选择数量较充足的类别作为目标类, SVDD方法通常可以得到较好的结果。
从预测试验的TS评分看, 用SVDD方法作暴雨预报还不是非常理想, 特别是空报较多, 还有待进一步的工作。众所周知, 除了预报方法本身, 预报因子的选择对方法的效果也起着至关重要的作用。本文的试验中, 因子选用的是暴雨发生以前24 h的高空资料, 对于本身具有不可预报性的突发性暴雨和中小尺度暴雨来说, 这些因子已经无法进一步提高预报准确率。如果能够应用数值预报产品来训练预测模式, 效果肯定会有所提高。但对于类似SVDD的需要大量训练数据的统计学方法而言, 为其补全过去几十年的数值预报数据是不现实的。如何让可利用的数值预报数据参与模型训练和预测, 即研究所谓样本因子不等长的SVDD方法是下一步的工作。
| [1] | 边肇祺, 张学工. 模式识别. 北京: 清华大学出版社, 2000: 296-320. |
| [2] | 王永庆. 人工智能. (第一版). 西安: 西安交通大学出版社, 1994: 16-19. |
| [3] | Vapnik V N. Statistical Learning Theory. John Wiley & Sons, Inc, New York, 1998. |
| [4] | Vapnik V N, The Nature of Statistical Learning Theory. Springer Verlag, New York, 2000. |
| [5] | Cristianini N, Taylor J S, An Introduction to SVMs and Other Kernel-based Learning Methods. UK: Cambridge Univ Press, 2000. |
| [6] | Tax D M J, Duin R P W, Support vector domain description. Pattern Recognition Letters, 1999, 20, (11-13): 1191–1199. DOI:10.1016/S0167-8655(99)00087-2 |
| [7] | 陈永义, 俞小鼎, 高学浩, 等. 处理非线性分类和回归问题的一种新方法 (Ⅰ)——支持向量机方法简介. 应用气象学报, 2004, 15, (3): 345–353. |
| [8] | 冯汉中, 陈永义, 成永勤, 等. 双流机场低能见度天气预报方法研究. 应用气象学报, 2006, (1): 96–101. |
| [9] | 赵国令, 肖科丽. 支持向量机方法在天气预报中的应用. 陕西气象, 2004, (6): 1–4. |
| [10] | 冯汉中, 陈永义. 支持向量机回归方法在实时业务预报中的应用. 气象, 2005, 31, (1): 41–44. |
| [11] | 车怀敏, 冯汉中. 支持向量机方法在德阳降水分类预报中的应用试验. 四川气象, 2004, 24, (2): 13–16. |
| [12] | Tax D, Ypma A, Duin R. Support Vector Data Description Applied to Machine Vibration Analysis//Boasson M, Kaandorp J, Tonino J, et al. Proc 5th Annual Conference of the Advanced School for Computing and Imaging (Heijen, NL, June 15-17), 1999: 398-405. http: // citeseer, ist. psu. edu/ tax99support, html. |
| [13] | Tax D M J, Duin R P W, Outlier detection using classifier instability. Lecture Notes in Computer Science, 1998, 1451: 593–601. DOI:10.1007/BFb0033222 |
| [14] | Tax D M J, Duin R P W. Data Description in Subspaces//Sanfeliu A, Villanueva J J, Vanrell M, et al. Proc 15th Int Conference on Pattern Recognition and Neural Networks (ICPR15). Los Alamitos: IEEE Computer Society Press, 2000, 2: 672-675. |
| [15] | Tax D M J, One-class Classification: Concept-learning in the Absence of Counter-examples. Delft University of Technology, 2001. |
 2007, 18 (5): 676-681
2007, 18 (5): 676-681