2. 中国气象局培训中心, 北京 100081
2. China Meteorological Administration Training Center, Beijing 100081
经典的最小二乘法和回归模型在气象和地学统计中有着极为广泛的应用[1-7]。实际应用中, 无论是建立统计分析预报方程, 还是求解数学物理方程的一些系数[8], 大都需要应用最小二乘法来估计计算的。众多的研究者为提高计算速度和改善计算精度对最小二乘法做了大量的改进, 但这些工作大多集中在实数域内。实际信号处理应用中也经常面临复数域信号[9], 目前一般都把复数信号转化为实数域的问题来处理, 最近我国学者已经注意到这方面的问题[10]。某些统计方法推广到复数域内后, 就富有了新的意义, 比如传统的EOF分离出来的仅是空间驻波振动分布结构, 而复经验正交函数分解 (CEOF) 就能够分离气象变量场中空间尺度行波分布结构以及位相变化[11-13], 从而比原EOF方法能揭露出更多的信息。显然把最小二乘法推广到复数域内也应当具有相当的价值和意义。
复数的形式在大气科学领域中不少, 如全球谱模式中的球谐系数为复数。文献[14]应用复最小二乘法去解决如何确定复自忆系数的问题, 为建立全球自忆谱模式奠定了基础, 应用于对500 hPa高度场的预报, 取得了较好效果[15]。本文试图把它作为一种方法提炼出来, 并以此为基础建立了一个复数自回归预报模型。利用一个任意给定的复数序列和对全国160个基本气象台站上历年7月月平均气温的预报作为两个实例, 来说明复最小二乘法和复数自回归模式与实数中的最小二乘法的差别, 以及与将实部和虚部分开来计算结果的差别, 展示复最小二乘法和复数自回归模式的优势。
1 对复最小二乘的数学推导不失一般性, 设有因变量y与p个自变量x1, x2, …, xp, 它们都是经过距平化后的复数, 相应地设有复线性相关模型:
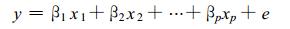
|
(1) |
式 (1) 中, β1, β2, …, βp为复系数, e为复数误差项。如何用一组样本来确定复系数β1, β2, …, βp的估计, 就是要解决的问题。
为研究y与x1, x2, …, xp之间的关系, 这里也就是确定复系数β1, β2, …, βp, 作n次采样, 则因变量y的样本为:
y1, y2, …, yn。
而第i次采样的自变量为:
xi1, xi2, …, xip (i=1, 2, …, n)
在线性假定 (1) 下, 有如下方程组:
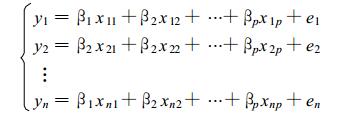
|
(2) |
写成矩阵形式:
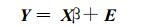
|
(3) |
其中Y, β, E为复变量, 分别为:

|
X为复因子矩阵:

|
其中, 元素yi, βi, ei, xij(i=1, 2, …, n; j=1, 2, …, p) 均为复数。
复系数b1, b2, …, bp的确定应使全部的拟合值ŷ1与实际值y1之差的模的平方和最小, 即满足
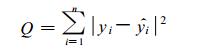
|
(4) |
为最小。
实际上Q是b1, b2, …, bp的非负二次项, 所以最小值一定存在, 根据微分学中极值原理, 有
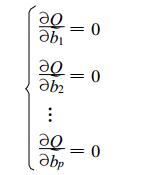
|
(5) |
这样计算确定复系数β1, β2, …, βp的估计b1, b2, …, bp的方法就是本文用到的复最小二乘法。由于b1, b2, …, bp都是复数, 不能如同实数领域内一样由式 (5) 直接求出。
将式 (4) 写成矢量形式:
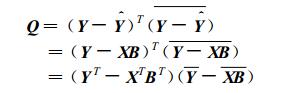
|
(6) |
其中Ŷ=(ŷ1, ŷ2, …, ŷn)T, ()T表示转置, ()表示共轭。
这样, 式 (5) 可以写为:
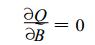
|
(7) |
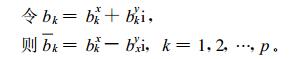
|
(8) |
bkx为实部, bky为虚部, bkx, bky均为实变量, i表示复数单元, 满足下列关系式:
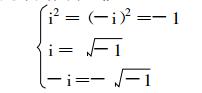
|
这样对b的求导, 便可转化为分别对实部bkx及虚部bky的求导。将Q的每一项具体写出:
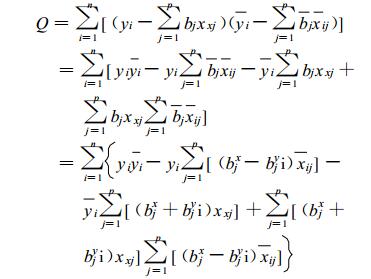
|
(9) |
Q对实部bkx求偏导:
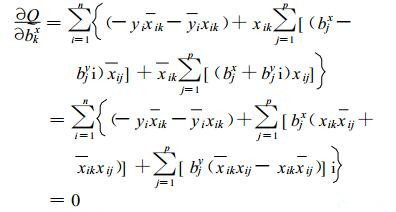
|
(10) |
k=1, 2, …, p。
同理, Q对虚部bky求偏导:

|
(11) |
k=1, 2, …, p。
由式 (10), 得
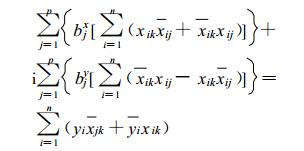
|
(12) |
k=1, 2, …, p。
由式 (11), 得
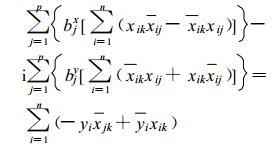
|
(13) |
k=1, 2, …, p。
式 (12) 和 (13) 合并, 整理得
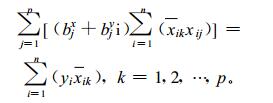
|
(14) |
将式 (8) 代入式 (14), 得

|
(15) |
将式 (15) 写成矩阵形式
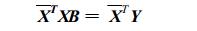
|
(16) |
或者
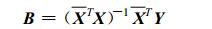
|
(17) |
()T表示转置, ()-1表示对距阵求逆。元素xij, bj, yj(i=1, 2, …, n, j=1, 2, …, p) 均为复数。
与传统的实数线形最小二乘法的估计公式[8] :
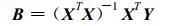
|
(18) |
作对照比较, 易见复数最小二乘法式 (17) 的唯一不同点在于矩阵X增加了共轭运算。
2 应用举例 2.1 简单例子先用一个简单的例子来说明复数域内与实数域内的最小二乘法的差异, 揭示在一个复数统计模型中, 将实部和虚部分开运算[16-17]存在的问题。
任意给出一个复数序列, X(实部, 虚部):
xi=(1, 3), (3, -2), (2, 1), (7, -2), (2, 7), (1, 5), (9, 9), (15, -3), (3, 15), (-2, -2), (-2, -2), (11, 7), (2, 5), (-1, -2), (14, 7), (2, 1), (7, 2), (3, -2), (9, 3), (7, 1), (2, 5), (3, 4), (6, 8), (4, -8), (5, 1), (-10, 4), (-4, 5), (10, 4), (5, 9), (5, 6), (5, 9), (3, 2), (10, 7), (2, 4), (10, 6), (-1, 8), (3, 6), (7, 2), (5, 6), (7, 8), (-9, 6), (-6, 0), (10, 2), (3, 5), (6, 9), (10, 5), (6, 5), (10, 3), (8, 9), (10, 8)。
i=1, 2, .., N(N=50)。
欲求出这一复数序列的自回归方程[8] :
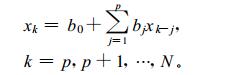
|
(19) |
取p=3, 若把实部和虚部分开, 各自应用实最小二乘法式 (18) 来计算, 可以得到B的估计值:
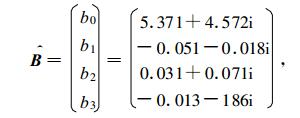
|
模拟与实况之间误差模的平方和为
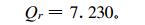
|
但使用式 (17), 则可以得到B的估计值:
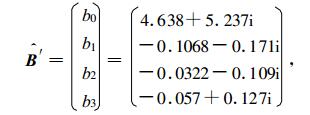
|
模拟与实况之间的误差模的平方和为
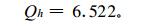
|
显然二者是不同的。真正复最小二乘法式 (17) 基础上的复自回归的模拟误差平方和比较小, 是前者的90%。这也说明对复数序列, 如果采用把实部和虚部分开, 采用实最小二乘法来分别计算, 是不能取得真正意义上的最小二乘, 因而也是不妥的。
2.2 我国大陆7月气温预报模型进一步的应用实例, 是应用复自回归模式制作全国160站7月的月平均气温预报。
为数学处理上的方便, 同时也考虑到我国冷空气活动过程通常是由北到南, 台风由南向北的基本特征, 将160个站点按纬度顺序排列, 对1951—2004年, 每年7月平均气温距平作一维离散傅立叶展开[18-19] :
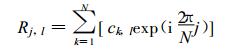
|
(20) |
式 (20) 中, Rj, l表示160站的7月月平均气温距平,
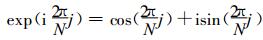
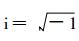

|
(21) |
这样, 即可将空间上的气温距平转换成离散的傅氏级数, 每年7月160站的月平均气温距平转换为由160个复数构成的序列, 每一个复数表示不同波数的振幅和位相, 同一波数的不同年份组成一个时间序列。亦即利用历史资料求出ck, l, 把每个波数k分量的ck, l, 按年代l排列成时间序列构成一个复数序列, 用复自回归方程:
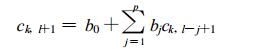
|
(22) |
按照上面推得的式 (17) 确定复自回归系数bj(j=0, 1, …, p) 后, 代入式 (22) 计算得到下一年 (l+1) 的傅氏系数ck, l+1=ak, l+1+bk, l+1i的预报值, 再应用式 (20), 就可得到预报年代各站点上的月平均气温距平预报值。经过实际计算取p=3或2为较好, 这里取为3。
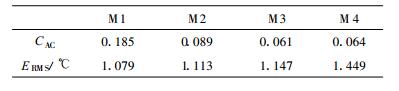
对1980—2004年, 共25年进行了后预报试验。对预报结果, 计算其与实况的距平相关系数CAC和均方根误差 (ERMS) 检验等, 并分别与其他3个常用的统计预报模型的相应预报进行比较。表 1列出对4个预报模型所作25年预报的两种检验平均值。表中M1(方法一) 表示对上述3阶复自回归模型的预报检验。M2(方法二) 是对实部和虚部分开各自按实最小二乘法式 (18) 计算的3阶自回归预报的检验。M3(方法三) 是对单站3阶实数自回归预报的检验。M4 (方法四) 是对持续性预报结果的检验。下面给出检验公式:
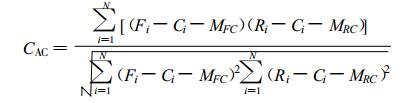
|
(23) |
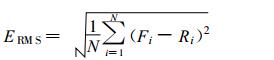
|
(24) |
其中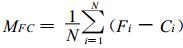
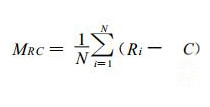
|
|
表 1 各种方法预报7月气温的CAC, ERMS多年平均 Table 1 The averaged CAC and ERMS of July temperature forecasted by 4 methods |
可以看出, 基于复最小二乘法的复自回归预报 (M1) 与实况的距平相关系数达到CAC=0.185, 均方根误差ERMS=1.079, 都好于其他3种方法的平均预报结果。方法三 (M3), 即单站3阶实数自回归预报的CAC评分效果最差。持续性预报 (M4) 的均方根误差 (ERMS) 最大。正如第2章中所述, 方法二 (M2) 即实部与虚部分开计算的3阶自回归预报效果, 与方法一有较大的差距, 但稍好于M3及M4。也说明实部与虚部分开来计算, 是不能得到复自回归系统真正意义上的最小二乘估计的。以前认为持续性预报 (M4) 有一定的技巧[20], 但这里25年的预报效果较差, 可能与气候变化的阶段性有关[21]。为了检验本文所述方法的适应性, 计算了1—12月的预报检验, 结果显示M1对每个CAC最大, ERMS最小, 预报效果比较稳定。
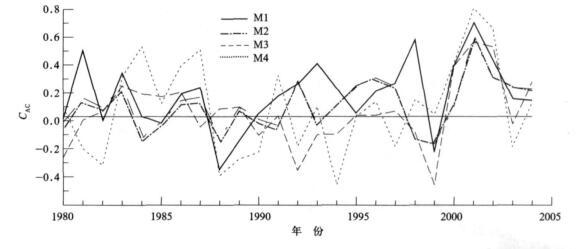
图 1绘出各种方法逐年7月气温预报的CAC检验结果, 也表明方法一 (M1) 的预报效果好于其他3种方法: ① M1预报的CAC值高于另3种方法的有9年, 即1981, 1983, 1990, 1992, 1993, 1994, 1997, 1998年和2000年, 而M2只有2年, M3只有4年, M4只有7年; ② M1预报的CAC>0.40有5年, 即1981, 1993, 1998, 2000年和2002年, 而M2只有1年, M3只有2年, M4只有4年; ③ M1预报失败CAC < 0.0的却只有3年, 即1985, 1988年和1989年, 而其他3种方法多达7年或8年。25年中, 只有2001年例外, 4种方法预报的CAC值都较高, 彼此相差不大。
|
|
| 图 1. 对4种统计预报模型逐年7月气温预报的CAC检验结果 Fig 1. Yearly CAC of July temperature forecasted by 4 methods | |
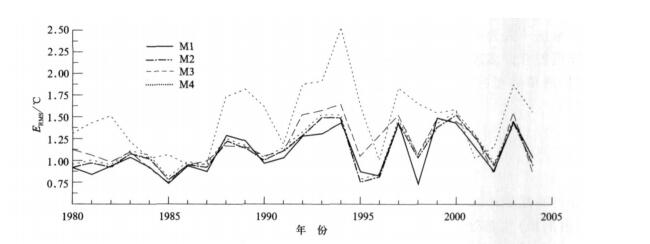
由图 2可知, 复自回归模型 (M1) 预报的7月气温ERMS相对较小又较稳定: ① M1预报的ERMS值小于其他3种方法的多达11年, 即1980, 1981, 1983, 1987, 1990, 1991, 1992, 1993, 1994, 1997年和1998年, 而M2只有8年, M3只有5年, M4只有1年; ② M1预报的ERMS在25年中的最大值也小于其他3种方法, 它是1999年的1.484 ℃, 而M2的最大值是2000年的1.525 ℃, M3是1994年的1.610 ℃, M4是1994年的2.498 ℃。
|
|
| 图 2. 对4种统计预报模型逐年7月气温预报的ERMS检验结果 Fig 2. Yearly ERMS of July temperature forecasted by 4 methods | |
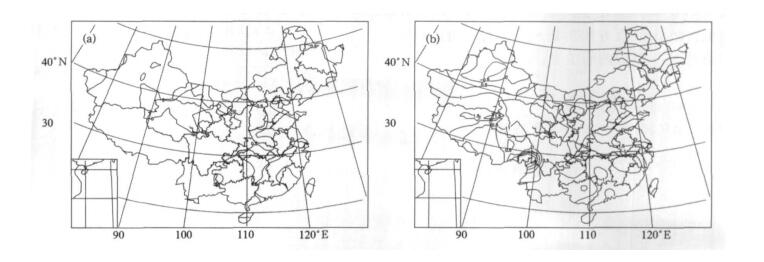
作为一个实例, 图 3绘出复数自回归模型 (M1) 对1998年7月的预报和实况对比, 可见有较好的效果: ①预报出了大部分地区的月平均气温正距平, 当然强度上有差异; ②对东北北端、黄河河套西北端、苏北-皖北-鲁南-豫东一带、湖南中南部及福建中南部等地的较高正距平, 预报得较好; ③对西北新疆北端、天山南鹿-新疆东部、西藏南部、西南的广西-云南-四川和贵州南部一带、以及四川东端、江西北部地区的较低正距平, 也预报得较好; ④准噶尔盆地的月平均气温负距平在预报中也有体现。当然也有一些较小范围的预报失败:如青海北部-河西走廊、内蒙古东北部、吉林东部、新疆喀什附近、宁夏北部等地区。
|
|
| 图 3. 方法一对1998年7月的预报 (a) 和实况 (b) Fig 3. Monthly temperature anomalies in July 1998 forecasted by the M1 (a) and observations (b) | |
为什么复最小二乘法具有这样的优势?可以从两个方面来分析:其一将160站的月平均气温距平场从实空间转换到傅氏空间复数序列, 傅氏系数表征的是整个物理场的特征, 即位相和振幅, 从而分离出比实空间更多的信息, 这与其他复数的统计分析方法[11]是一致的, 这一步也是采用复最小二乘法的出发点; 其二, 由于采用复最小二乘法计算式 (17), 从而得到了真实意义的“最小二乘估计”, 模拟和预报的效果要优于单独采用实最小二乘法计算得到的结果。因此, 欲对傅氏系数这类复数序列进行分析研究, 复最小二乘法不失为一种行之有效的方法。
当然, 也还可能有许多改进之处, 如采用聚类分析方法等来代替简单地按纬度顺序排列, 其预报效果可能会更好些。
3 结语1) 本文得到的复最小二乘法是经典的最小二乘法在复数域内的推广, 是处理复数序列的有效方法。以此为基础可以把许多统计学中的方法推广在复数域内, 形成复数域内的特有统计方法, 如复线性回归、复非线性回归方程, 复均生函数等。
2) 应用实例表明, 从实空间到傅氏空间的转换, 可以得到比实空间更多的信息, 这是进行复最小二乘法的基础。
3) 实际计算表明, 对复数采用实部和虚部分别计算处理, 得不到真实意义上的最小二乘估计, 因而也是不妥的。使用复最小二乘法的自回归预报, 模拟和预报的效果都要好于其他方法。由此可见, 开展复数域内统计预报方法的研究是有前途的, 而复最小二乘法是一种有效的工具。
| [1] | 科恩A, 科恩M. 数学手册. 周强民, 孙山泽, 王跃东, 译. 北京: 工人出版社, 1987: 530-534. |
| [2] | 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 1990: 51-59. |
| [3] | 么枕生. 气候统计学基础. 北京: 科学出版社, 1984: 191-199. |
| [4] | 曹鸿兴. 局地天气预报的数据分析方法. 北京: 气象出版社, 1983: 133-138. |
| [6] | 安鸿志, 顾岚. 统计模型与预报方法. 北京: 气象出版社, 1986: 22-36. |
| [7] | 盛聚, 谢式千, 潘承毅. 概率论与数理统计. (第二版). 北京: 高等教育出版社, 1995: 279-290. |
| [8] | 郭秉荣, 史久恩, 丑纪范. 使用多时刻历史资料的动力-统计长期天气数值预报模式∥第二次全国数值天气预报会议论文集. 北京: 科学出版社, 1980: 115-126. |
| [9] | Dash P K, Jena R K, Panda G, et al. An extended comp lex Kalman filter for frequency measurement of distorted signals. IEEE Trans Instrumentation and Measurement, 2002, 49, (4): 1569–1574. |
| [10] | 崔博文, 陈剑, 陈心昭, 等. 复参数最小二乘估计方法. 安徽大学学报 (自然科学版), 2005, 29, (3): 7–10. |
| [11] | Rasmusson E M, Arkin P A, Chen W Y, Biennial variation in surface temperature over the United States as revealed by singular decomposition. Mon Wea Rev, 1981, 109: 587–598. DOI:10.1175/1520-0493(1981)109<0587:BVISTO>2.0.CO;2 |
| [12] | Barnett T P, Interaction of the monsoon and Pacific trade wind systems at interannual time scales.Part Ⅰ :The equatorial zone. Mon Wea Rev, 1983, 111: 756–773. DOI:10.1175/1520-0493(1983)111<0756:IOTMAP>2.0.CO;2 |
| [13] | 魏凤英. 现在气候统计诊断预测技术. 北京: 气象出版社, 1999: 134-140. |
| [14] | 谷湘潜. 一个基于大气自忆原理的谱模式. 科学通报, 1998, 43, (9): 909–917. |
| [15] | 曹鸿兴, 谷湘潜. 自忆谱模式对中期环流预报的改进. 自然科学进展, 2001, 11, (3): 308–313. |
| [16] | Hasselmann K, Barnett T P, Techniques of linear prediction for system with periodic statistics. J Atmos Sci, 1981, 38: 2275–2283. DOI:10.1175/1520-0469(1981)038<2275:TOLPFS>2.0.CO;2 |
| [17] | 江剑民. 北半球500毫巴候平均图的波谱分析和预报. 气象学报, 1983, 41, (4): 433–443. |
| [18] | 李庆扬, 王能超, 易大义. 数值分析. 武汉: 华中工学院出版社, 1982: 105-107. |
| [19] | 徐士良. C常用算法程序集. (第二版). 北京: 清华大学出版社, 1996: 266-270. |
| [20] | 曹鸿兴, 谷湘潜. 一种集成技术———最优调和法. 气象, 1999, 25, (5): 3–6. |
| [21] | 章基嘉, 葛玲. 长期预报基础. 北京: 气象出版社, 1983: 210-213. |
 2007, 18 (4): 435-441
2007, 18 (4): 435-441