应用气象学报  2007, 18 (4): 417-426   PDF    
引用本文
郑照军, 刘瑞霞, 刘玉洁. 利用高程数据修正NOAA AVHRR轨道定位信息[J]. 应用气象学报, 2007, 18(4): 417-426.
Zheng Zhaojun, Liu Ruixia, Liu Yujie. Correction to the Localization of NOAA AVHRR with DEM[J]. Journal of Applied Meteorological Science, 2007, 18(4): 417-426  
利用高程数据修正NOAA AVHRR轨道定位信息
郑照军1,2, 刘瑞霞2, 刘玉洁2     
1. 北京大学物理学院大气科学系, 北京 100871;
2. 中国气象局中国遥感卫星辐射测量和定标重点开放实验室 国家卫星气象中心, 北京 100081
2006-07-30 收到, 2007-01-31 收到修改稿.
资助项目: 国家自然科学基金项目 (40501048) 和国家科技部基础条件平台工作 (2005DKA31700) 共同资助    
摘要: 在没有考虑高程数据的预处理方法得到的NOAA AVHRR资料中, 每条扫描线数据中的51点经纬度定位信息常常有误差, 尤其是在海拔较高、距卫星星下点较远的定位点, 其定位信息与实际差别很大。针对这种情况, 该文描述了一种引入高程数据并结合51点定位信息对2048个扫描点定位进行快速、简易的订正方法, 可有效地修正AVHRR资料预处理未考虑高程信息引起的经纬度定位偏差, 以便于对分辨率和定位精度要求不高的用户更好地使用AVHRR数据。
关键词: 高程数据    修正    AVHRR    定位    
Correction to the Localization of NOAA AVHRR with DEM
Zheng Zhaojun1,2, Liu Ruixia2, Liu Yujie2     
1. Department of Atmospheric Science, School of Physics, Peking University, Beijing 100871;
2. Key Laboratory of Radiometric Calibration and Validation for Environmental Satellites, China Meteorological Administration (LRCVES/CMA), National Satellite Meteorological Center, Beijing 100081
Abstract: Errors can often be found in the 51 longitude and latitude location information of each scan line in the NOAA AVHRR data which are preprocessed without taking the Digital Elevation Model (DEM) into consideration, and are dramatically huge at the points with high altitude and far from the nadir.The simulation indicates that the horizontal location bias will be increased with the increasing of the zenith angle.This bias caused by the location error can reach the kilometer order level and is mainly displayed in the longitude direction, with small weight of the latitude direction.It is necessary to correct this deviation.Even to the users who project first and then re-correct with the surface control-point, orientation correction can reduce the difficulty in re-correction and improve the orientation precise. A quick and simple method is developed by which localization information of 2048 satellite observation points in a scan line can be corrected with DEM and that of 51 original localization points in AVHRR L1B data. Firstly, latitudes and longitudes of 2048 satellite observation points are figured out using 51 original localization points' information by equidistance interpolation of one variable in an entire siding-to-siding block.Simultaneously the altitude of each point is looked up from DEM data.Secondly, one points is located exactly and the other is not revised.The horizontal location bias (i.e., spherical surface radian deviation) of which the former is relative to the latter can be achieved with DEM and the uncorrected point latitude and longitude.Thirdly, new localization information of the inaccurate point is calculated by dint of original localization points information and spherical surface radian deviation, and then the correction is finished.Because DEM influence to the location of several points at nadir is minimal, they can be considered as original points located exactly and then those on both sides are set as ones to be revised.Thereupon corrections can be carried out from nadir to verge step by step.The method can effectively decrease orientation errors in AVHRR data without the altitude information, which will contribute to the better use.
Key words: DEM     correction     AVHRR     localization    
引言

NOAA卫星轨道高度约为850 km, 其搭载的AVHRR (Advanced Very High Resolution Radiometer) 在±55.58°扫描角范围内对地面进行探测。地球形状、自转, 卫星速度、姿态变化、轨道偏移, 传感器扫描角的非线性误差和采样延迟等, 均可引起图像畸变[1-3]。

通常, 将AVHRR数据定位按其实现方式及精度要求的不同划分为3个步骤[4], 即直接定位[5-7]、导航定位[8-10]和几何精校正[11-13]。当前, 国内各卫星台站提供的AVHRR L1B数据, 其预处理过程中的定位环节, 大都只考虑直接定位, 比如大家熟知的中国气象局国家卫星气象中心AVHRR 1A.5数据 (也属于L1B数据) 就是这样。

直接定位就是基于卫星轨道报 (ephemeris, 也称星历表) 数据、卫星轨道外推模型以及接收信息中的时间信息直接确定观测时刻的卫星位置, 然后根据卫星扫描特性及卫星姿态, 计算出卫星各个瞬时视场所得到的地面观测点的地理经纬度信息[4-7]。

AVHRR L1B数据的使用者, 关注利用数据中51点地理位置信息获取其他探测点的经纬度方法[6, 14], 这也是利用地面控制点 (GCPs) 对AVHRR图像进行几何精校正的前提[4]。L1B数据中的51点地理位置信息是利用AELDS系统产生的[5], NOAAKLM用户手册提供了线性插值、拉格朗日插值等获取其他探测点的经纬度的方法, 但这些方法的精度依然离不开51点地理位置信息的精确性。

宏观上, 地球可以看作一个椭球体。但地球表面并不光滑, 海洋、山地、高原、平地交错分布, 从而有了高程 (即地形高度) 差异。一般国内台站提供的AVHRR L1B数据, 在51点地理位置信息的计算过程中, 往往不考虑高程因素, 而把地球当作理想椭球体处理, 这样势必带来定位偏差[15-18]。

本文将从原理上指出忽略高程信息造成的AVHRR L1B数据直接定位偏差, 并提出一种不对L1B数据重新做预处理, 而是利用高程数据直接修正该偏差的方法。这种修正不是仅针对一条扫描线中的51定位点, 而是推广到2048个扫描点。

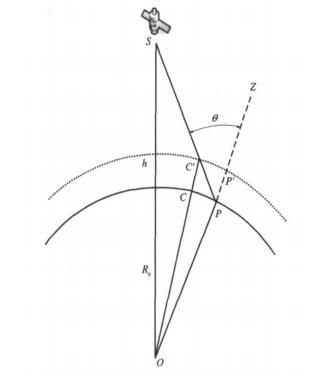
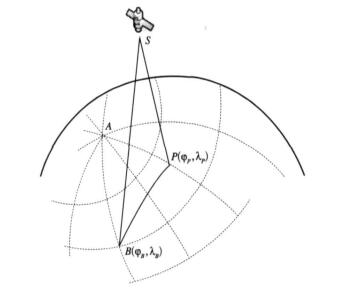
1 高程对定位的影响

在图 1中, S点为卫星所处位置, O点为地球球心, P点为没有考虑高程的地球球面上的一点, 与地心O点的距离为地球半径Re, P′点为海拔高度为h的地球球面上的一点, 与地心O点的距离为Re+h, OZ为从地心出发过P, P′点指向天顶的射线, SP与OZ之间的夹角θ为P点的卫星天顶角[19]。

图 1. 高程对计算卫星观测点位置的影响关系示意图 Fig 1. The impact of elevation on the satellite observation point position calculation

在未考虑高程数据的预处理方法中, 卫星实际观测到的C′点被认为是P点。将C′点投影到没有考虑高程的P点所在球面上, 投影点为C点, 由于C′点和C点对应的经纬度相同, 因此, 未考虑高程数据引起的经纬度定位偏差就是P点和C点的位置差。在O, P, P′, C′, C构成的图形中, 有这样的关系式成立

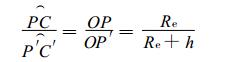
(1)

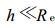
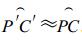
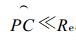
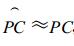
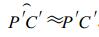
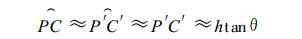
由于, 故Re+h≈Re, 即。又因为, 即∠POC是个很小量, 所以, , ∠OPC=∠OP′C′≈90°, 从而有

(2)

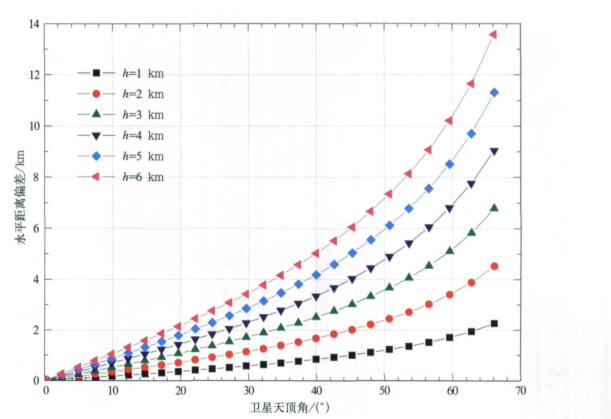
显然, P点和C点的水平直线距离 (以下称水平距离偏差) 与卫星天顶角以及高程差有关。彩图 2给出了不同高程引起的水平距离偏差随卫星天顶角的变化关系。在靠近星下点处, 水平距离偏差很小, 可以忽略不计。随着卫星天顶角的增加, 水平距离偏差逐渐增大, 且海拔越高, 偏差越大。如1 km的高程, 在45°卫星天顶角处, 将引起同等大小的水平距离偏差, 在63°卫星天顶角附近, 则将引起两倍高程的水平距离偏差。考虑到中国的地形特点, 海拔高度在1 km以上的区域占了陆地的三分之二, 而广袤的青藏高原的平均海拔高度更是接近4 km; 同时, 在一条AVHRR扫描线的2048个扫描点中, 卫星天顶角不超过45°的只占70%, 扫描线两端的扫描点, 其卫星天顶角达66°。可见, 如果预处理不考虑高程影响, 由定位偏差引起的水平距离偏差数量级将达到公里级。

图 2. 不同高程引起的水平距离偏差随卫星天顶角的变化 Fig 2. The horizontal range bias caused by the different elevation along with the satellite zenith change

当然, 水平距离偏差并不等于经纬度定位偏差, 这不仅是因为经纬度偏差是两个方向上的, 而且同等大小的水平距离偏差在地球表面不同处引起的经纬度偏差也不相同, 以1 km水平距离偏差为例, 在赤道附近, 在东西或南北方向将对应0.009°的经度或纬度偏差, 随着纬度的增加, 南北方向上的纬度偏差基本不变, 而东西方向上的经度偏差将近似以纬度的正割函数增加。可见, 对未考虑高程数据的预处理定位信息进行订正十分必要。

2 利用高程修正定位信息的方法 2.1 试验资料的选取

采用的高程数据DEM来自USGS的GTOPO30。该数据为全球高程, 等经纬度投影, 分辨率为“30弧秒×30弧秒”, 即“0.008333333333333°×0.008333333333333°”。高程修正过程中使用的是该数据再处理生成的新数据:先将GTOPO30重采样为“0.01°×0.01°”, 再采用“7×7”点滑动平均。在使用高程数据查找地表某点的高程时, 可以由该点的经纬度计算出其对应于高程数据文件中二维数组的行列号, 直接将该行列号处的高程取出即可。

采用的轨道数据来自国家卫星气象中心接收处理的2005年9月2日04:43(世界时) 的NOAA-17 AVHRR/3轨道数据。该数据属于L1B级, 预处理中的定位没有考虑高程影响, 数据格式为1A.5。

2.2 修正方法

利用高程数据修正未考虑高程影响的预处理定位信息, 可以采用递推方式, 即选定两个定位点, 其中一个定位准确, 这样就可以利用该点经纬度和另一点经纬度及其对应的高程计算出另一点的位置偏差, 从而修正另一点的定位信息。图 3、图 4描绘了这一过程。

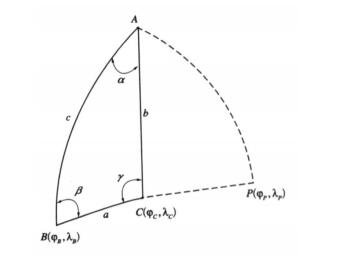
图 3. 卫星及其对地观测的一条扫描线中两个定位点的示意图 Fig 3. The sketch of the satellite ubiety and two location points in a scan line

图 4. 利用高程对定位点进行修正的示意图 Fig 4. The sketch of the revision to the location points with DEM

图 3中, A是北极点, B, P分别是卫星S对地观测的同一条扫描线中两个定位点, 与之对应的纬度是φB, φP, 经度是λB, λP; AB, AP分别是过B点和P点的经度线, 二者经度差Δλ=λP-λB, 即两个定位点的经度差。∠ABP是P点相对于B点的方位角, 其以正北方向为0°, 并作为起点按顺时针方向计算。BP是B, P两点在地球表面的连线, 它是地球表面的一段弧长, 同时也是B点和P点对地心的夹角。

图 4是图 1和图 3地表部分的综合显示图, 它描绘了球面三角形ABP和ABC的相关信息 (需要特别指出, B, P两点的距离一定要足够大, 否则会出现C点不在B, P两点之间的情况, 即不满足图 4所示关系, 从而无法应用以下订正方法)。其中, A, B, P 3点及描述信息与图 3相同, P, C两点及描述信息与图 1相同, C点的经度、纬度分别为λC, φC。球面三角形ABC的三个内角分别为α, β, γ, 实际上它们属于二面角, a, b, c分别是α, β, γ的对边弧度。α可表示为λC-λB (不失一般性, 假定λC≥λB), b, c可分别表示为π/2-φC, π/2-φB, 而根据式 (2), 设的弧度为δ, 的弧度a可以近似地表示为δ-htanθ/Re。

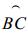
对P点的修正, 实际上就是求取C点的经纬度λC和φC, 这可以利用B, P两点的纬度、经度φB, φP, λB, λP以及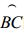的弧度a, 由球面三角数学公式推导得到。

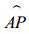
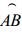
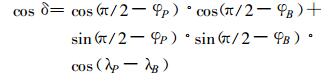
在球面三角形ABP中, ∠BAP=λP-λB(不失一般性, 假定λP≥λB), 的弧度为π/2-φP, 的弧度为π/2-φB, 依据球面三角形余弦公式有

(3)

进一步推导得到

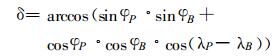
(4)

在球面三角形ABP中, 依据球面三角形余弦公式有

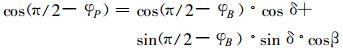
(5)

进一步推导得到

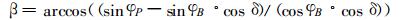
(6)

在球面三角形ABC中, 依据球面三角形余弦公式有

(7)

进一步推导得到

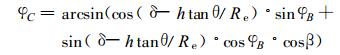
(8)

在球面三角形ABC中, 依据球面三角形正弦公式有

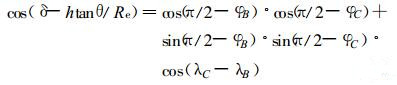
(9)

进一步推导得到

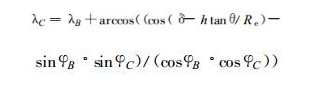
(10)

由以上式 (4)、(6)、(8)、(10) 依次计算, 即可得到C点的经纬度λC和φC, 完成对P点经纬度偏差的简易和快速修正。

对于一条扫描线而言, 可以借助AVHRR L1B数据中提供的51点定位信息, 先采用精度优于线性插值的一元全区间等距插值方法[20], 计算出2048个扫描点的经纬度和卫星天顶角, 并从高程数据文件中查找出2048个扫描点对应的高程, 然后开展由星下点 (第1024和第1025点) 向扫描线两侧 (分别向第1和第2048点方向) 进行的高程递推定位修正。具体方式为:先以第1024和第1025点为起始基准点, 对于第1023到第1005点、第1026到第1045点的修正, 均分别以第1025和第1024点为基准点; 对于第1004到第1点范围内第n点的修正, 以修正过的第n+20点为基准点; 对于第1046到第2048点范围内第n点的修正, 以修正过的第n-20点为基准点。

基准点之所以采用上述选取方式, 主要原因有两点:①如果基准点与被修正点距离太近, 订正后的点不在基准点与被修正点之间, 导致订正公式不成立; ②如果基准点与被修正点距离太远, 出现理论误差, 导致订正后的点偏离扫描线方向太多, 失去修正意义。

本文提供了一个FORTRAN语言子程序 (参见附录), 用于根据一条扫描线2048个扫描点的经纬度及其对应高程和卫星天顶角信息, 对2048个扫描点定位信息进行修正。

需要说明的是, 本文的推导公式中用到的经纬度仅针对中国区域, 因中国区域地处东半球、北半球, 纬度和经度都是正值, 不需要考虑跨赤道、跨本初子午线的情况。当然, 也可以利用上面的修正方法做全球数据定位偏差修正, 但要考虑经纬度值范围, 这里不再赘述。

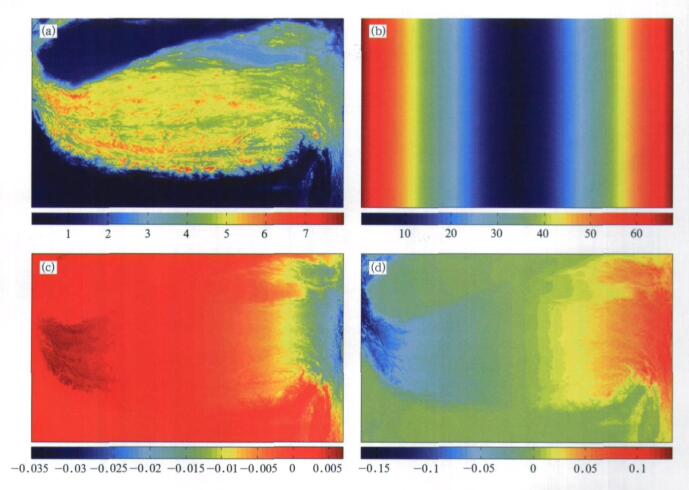
2.3 结果分析

应用上述方法对选取的试验数据进行定位修正, 为了突出高程对定位的影响, 以覆盖青藏高原地区的数据进行修正, 彩图 5给出了经纬度修正量大小与高程和卫星天顶角的修正效果对比。表 1为彩图 5相应各物理量统计值。彩图 6、彩图 7分别为利用修正前和修正后扫描点投影后的AVHRR图像。

图 5. 经纬度修正量大小与高程和卫星天顶角的对比 （a）高程（单位：km），（b）卫星天顶角（单位：（°）），（c）修正后与修正前的纬度差（单位：（°）），（d）修正后与修正前的经度差（单位：（°）） Fig 5. The sizes of longitude and latitude revision contrasted with elevation and satellite zenith (a) elevation (unit:km), (b) satellite zenith (unit:(°)), (c) latitude difference between after and before revision (unit:(°)), (d) longitude difference between after and before revision (unit:(°))

表 1 彩图 5各物理量统计值 Table 1 The statistic of various physical quantities in Fig. 5

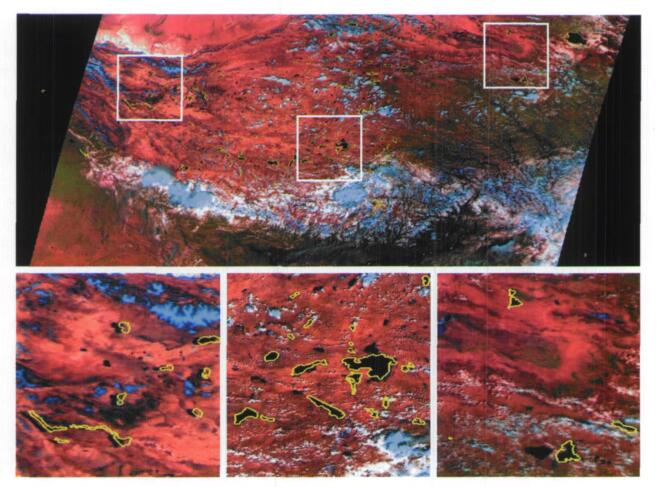
图 6. 利用修正前的定位点线性插值投影后的NOAA AVHRR图像 Fig 6. The NOAA AVHRR projection image from orbital date before location point revision by linear interpolation

图 7. 利用修正后的定位点线性插值投影后的NOAA AVHRR图像 Fig 7. The NOAA AVHRR projection image from orbital date after location point revision by linear interpolation

无论从彩图 5还是从彩图 6和彩图 7的整体或局部放大对比来看, 定位修正前后, 星下点附近像素位置没有太大变化, 但对于远离星下点区域, 修正前的像素普遍向远离星下点的扫描方向偏离3到10个像元, 最大达13个像元, 而卫星飞行方向的偏离基本不超过1个像元; 修正后, 所有像素的偏离都不明显, 达到了比较好的定位修正效果。

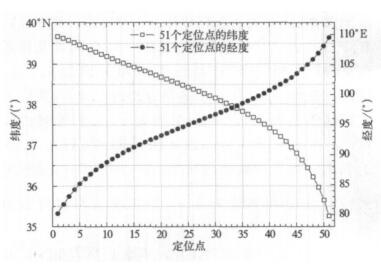
对于纬向偏差大于经向偏差的情况是可以理解的。以中纬度地区 (35°~40°N) 的一条扫描线为例 (见图 8), 第1个与第51个定位点的纬度相差4.400°, 而经度相差26.691°。由于定位偏差基本沿扫描方向, 因此, 高程引起的水平定位偏差也就主要表现在东西的经度方向, 南北纬度方向的分量则不大。

图 8. 中纬度地区一条扫描线中51个定位点的经纬度 Fig 8. The latitudes and longitudes of 51 localization-points in a mid-latitude scan line

实际上, 对于静止气象卫星 (如FY-2C) 而言, 如果在预处理过程中不考虑高程影响, 偏移效应同样存在, 对此也可采用上述方法进行订正。订正时, 所有被订正点均以星下点为基准点即可。不过, 由于静止气象卫星距离地球较远, 且像元尺度较大 (一般约为3~5 km), 对于圆盘图中靠近星下点的半数以上像元, 其订正量一般不超过1个像元, 而在远离星下点的地方, 订正量最大也就接近3个像元。假如考虑云的影响, 特别是高云, 偏移效应相对明显, 在知道云高的情况下, 同样可以采用上述方法进行订正。

3 结语

本文采用高程数据递推订正因预处理时未考虑高程影响而引起的定位偏差, 原理清晰, 方法简单易行, 计算快捷, 效果也比较好。当然, 这种订正方法也有一些缺点。比如, 假定高程在很小的水平距离内保持不变, 这只适合梯度变化不大的高原、丘陵等平坦地形, 对于突兀陡峭、粗糙度较大的山地, 原定位点和修正后定位点的位置, 往往有很大的高程差, 这势必导致过修正或少修正的情况发生。此外, 将椭球状地球看作规则圆球体, 近似地认为很小的球面圆弧为线段等, 这些假定都会对高程定位修正精度产生影响。

表 附录:利用高程数据修正NOAA AVHRR轨道定位信息的FORTRAN77源程序

参考文献
[1] 王光辉, 陈标, 何卫平. 基于球坐标变换的AVHRR 2048点经纬度的研究. 青岛大学学报, 2003, 16, (3): 45–48.
[2] 汤国安, 张友顺, 刘咏梅, 等. 遥感数字图像处理. 北京: 科学出版社, 2004: 60-66.
[3] MODIS Level 1A Earth Location: Algorithm Theoretical Basis Documnet.1997, http:∥modis.gsfc.nasa.gov.
[4] 张斌. 极轨气象卫星NOAA AVHRR数据的高精度定位. 清华大学学报, 1999, 39, (9): 81–85.
[5] Davison G J, Ground control pointing and geometric transformation of satellite imagery. Int J Remote Sensing, 1986, 7, (1): 65–74. DOI:10.1080/01431168608954661
[6] 刘良明, 廖明生, 朱攀, 等. NOAA气象卫星AVHRR 1A.5数据集的定位处理. 武汉测绘科技大学学报, 1998, 23, (1): 62–66.
[7] 刘林, 王海红, 胡松杰. 卫星定轨综述. 飞行器测控学报, 2004, 24, (2): 28–34.
[8] 张斌, 朱正中, 葛成辉, 等. NOAA AVHRR数据的高精度导航定位. 遥感学报, 1999, 3, (4): 259–267.
[9] Dybbroe A.Im proved navigation of Advanced Very High Resolution Radiometer Data at High Latitudes.2004, http:∥cimss.ssec.wisc.edu.
[10] Rosborough G W, Baldwin D G, Emery W J, Precise AVHRR image navigation. IEEE Trans Geo science & Remote Sensing, 1994, 32, (3): 644–657.
[11] 吴炳方. NOAA AVHRR 1B数据的几何精纠正. 环境遥感, 1994, 9, (4): 287–295.
[12] Parada M, Millan A, Lobato A, et al. Fast coastal algorithm for automatic geometric correction of AVHRR images. Int J Remote Sensing, 2000, 21, (11): 2307–2312. DOI:10.1080/01431160050029585
[13] 黄敬峰, 许红卫, 王人潮, 等. NOAA/AVHRR数据的几何精纠正方法研究. 浙江大学学报, 2000, 26, (1): 17–21.
[14] 师春香, 刘玉洁. 国外部分卫星产品质量评价和质量控制方法. 应用气象学报, 2004, 15, (增刊): 142–151.
[15] 邵永社, 何向晨, 陈鹰, 等. 飞行器定位中的地形起伏影响及修正方法研究. 系统工程与电子技术, 2006, 28, (3): 403–406.
[16] 程芦颖. 虚拟地形投影与地球同步卫星定位解全集. 武汉大学学报, 2005, 30, (7): 629–631.
[17] 隋立芬, 许其凤, 杨力. 高程及卫星轨道误差对Z坐标的影响. 测绘学院学报, 2000, 17, (2): 91–94.
[18] 林雪原, 何友, 张力. 高程误差对双星定位系统定位精度的影响研究. 武汉大学学报, 2005, 30, (12): 1039–1043.
[19] 陈渭民. 卫星气象学. 北京: 气象出版社, 2003: 173-175.
[20] 徐士良. FORTRAN常用算法程序集. (2版). 北京: 清华大学版社, 1995: 165-167.