2. 中国科学院大气物理研究所大气边界层物理和大气化学国家重点实验室, 北京 100029;
3. 94514 部队气象保障室, 济南 250002;
4. 中国科学院大气物理研究所竺可桢-南森国际研究中心, 北京 100029
2. State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, CAS, Beijing 100029;
3. Weather Guatantee Room of Troop 94514, Jinan 250002;
4. Nansen-zhu International Research Center, Institute of Atmospheric Physics, CAS, Beijing 100029
气候和中尺度数值模拟结果对近地层动量和热量通量极为敏感[1-2]。因此, 发展可应用于数值模式的近地层湍流通量参数化方案已经成为一个十分重要的研究领域[3-4]。半个多世纪以来, 作为近地层研究的基础, Monin-Obukhov[5]相似理论被广泛地应用于估算地气之间的湍流通量交换。在这一理论基础之上, 众多学者依据不同试验资料和分析方法, 相继提出了一系列参数化方案。其中, 1971年Businger等[6]分析了Kansas试验观测资料进而提出一组湍流通量廓线关系 (以下简称Businger71)。1974年Dyer[7]对之前二十多年不同学者所做的工作进行了总结分析 (Dyer74) 并修正了Businger71中的部分参数。1979年Louis[8]提出了适用于中尺度数值模式中无需循环迭代的新型参数化方案 (Louis79), 这一方案的提出对数值计算湍流通量产生了深远的影响。1982年, Louis等[9]对Louis79中部分参数和表达式进行了改进 (Louis82)。到目前为止, Louis79和Louis82因为其公式简单且无需循环迭代的特点而被广泛应用于气象模式中[10], 包括美国海军全球和区域模式以及欧洲中心中尺度天气预报GCM模式等[1, 3, 11]。1988年Holtslag等[12]提出了应用于夜间近地层陆面模式中的参数化方案 (Holtslag88), 1991年Beljaars等[13]给出了新的热量普适函数 (B & H91)。1995年Launiainen[14]给出了稳定度参数的解析式 (Launiainen95), 从而避免了循环迭代。针对Louis82存在的不足并结合Holtslag 88, 2002年Wang等[10]提出了新的参数化方案 (Wang02)。显而易见, 由于区域模式对湍流通量参数化方案的极端敏感性, 当这些不同的湍流通量参数化方案应用到气候和中尺度模式中可能使模拟结果产生重大差异。然而在模式中测试这些参数化方案存在一定困难:无法区分模拟结果的偏差是由于近地层参数化不足还是由模式其他部分引起的; 近地层以上的大气性质随着近地层通量的变化而变化。所以, 独立于模式之外, 对比分析这些参数化方案具有十分重要的意义[15]。
因此, 本文将利用GAME/Tibet试验的观测资料, 对比分析对于陆面下垫面而言在一定的近地层层结稳定度变化范围内, 由这些方案计算所得的湍流动量输送系数之间的差异, 以期为近地层湍流动量通量的数值计算提供参考依据。
1 对比分析选取1998年5—9月GAME/Tibet试验研究组在青藏高原上进行的加强观测中那曲通量观测站的观测资料, 对Businger71, Dyer74, Louis82, B & H91, Launiainen95和Wang02等六种参数化方案进行深入的对比分析, 其中各参数化方案的具体表达式详见相关文献[6-10, 12-14]。其中Businger71, Dyer74和B & H91三种方案在计算中必须通过循环迭代求解, Louis82和Wang02方案则是以Businger71方案为基础, 直接将湍流通量输送系数参数化为整体理查孙数和粗糙度的函数, 有效避免了循环迭代; 而Launiainen95方案则是通过给出稳定度参数与整体理查孙数之间的近似计算关系而避免循环迭代。
那曲站地处31.379°N, 91.9°E, 海拔4580 m[16]。那曲通量观测资料中有超声观测的时间区间为1998年7月15日至9月15日。其中由于天气影响以及仪器维护等原因, 观测资料不连续。为提高观测资料的可信度, 对其进行简单的质量控制。首先, 为保证风速观测值能够完全真实地反映大气流动性质, 避免由于绕流等因素所造成的影响, 首先从观测资料序列中挑选出风向来向朝着风速测量仪的那部分资料。另外, 当超声观测的瞬时风速本身较小, 计算得到的摩擦速度也很小时, 仪器误差将变得非常显著, 从而容易导致在计算CMobs时产生较大误差, 因此, 进一步挑选出其中摩擦速度≥0.2 m/s, 同时超声观测风速≥2.5 m/s的观测资料。最后, 得到可供应用于方案验证的样本总数为69, 其中稳定条件下共有39个资料点, 不稳定条件下共有30个资料点。
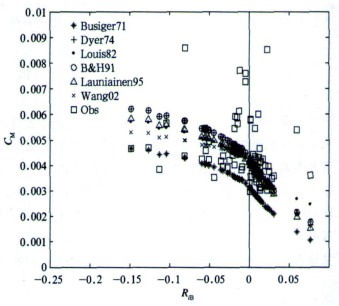
整体理查孙数RiB和湍流动量输送系数观测值CMobs可根据式 (1) 和 (2) 计算得到, CMobs随RiB的变化如图 1所示。
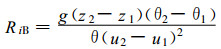
|
(1) |
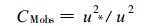
|
(2) |
|
|
| 图 1. 利用那曲站观测资料, 应用六种方案计算得到的湍流动量输送系数CM和观测得到的CMobs随RiB变化散点分布图 Fig 1. Plot of the turbulent momentum flux transfer coefficient (CM) calculated by six parameterization schemes with Naqu flux mesurements and the coefficient by observations (CMobs) varies according to RiB | |
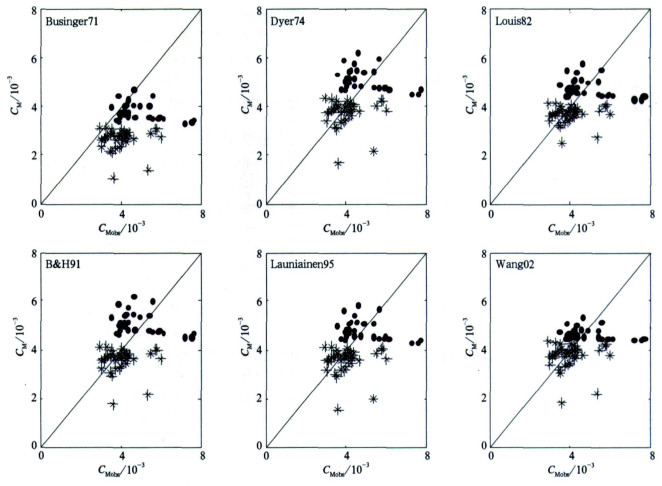
其中, 下标2表示观测高度z2为3.5 m, 下标1表示观测高度z1为1.3 m。θ2, θ1分别表示对应高度上的虚位温。θ为平均值。u2, u1分别为对应高度上慢响应风速观测值。u*和u分别为2.9 m处超声观测得到的摩擦速度和风速。下垫面为稀疏短草草原, 空气动力学粗糙度z0和热力粗糙度z0h的取值见参考文献[16], kB-1=4.62, 即z0h=z0/e4.62, 其中应用Louis82方案计算时取z0h=z0。观测高度z取为超声观测高度2.9 m。各方案计算得到的CM与CMobs之间的1:1比例图如图 2所示。
|
|
| 图 2. 利用那曲站观测资料, 应用六种参数化方案计算得到的湍流动量输送系数CM与观测得到的CMobs之间的1:1比例图 (*表示稳定条件, ●表示不稳定条件) Fig 2. The plot of the turbulent momentum flux transfer coefficient calculated by six parameterization schemes versus transfer coefficient determined by observation directly ("*" means stable condition and "●" means unstable condition) | |
参考Gao等[9]给出的误差分析方法, 分别计算了对应不稳定和稳定条件下各方案估算的CM相对CMobs的归一化标准差 (EN), 见表 1。EN定义为:

|
(3) |
|
|
表 1 六种方案分别应用那曲观测资料计算得到的CM相对CMobs的归一化标准差 (EN) Table 1 The normalized standard error of the estimation (EN) compared the CM calculated by six schemes to the CMobs determined by direct measurements |
式 (3) 中, Li表示应用参数化方案计算得到的湍流动量输送系数CM, Ci表示根据观测资料直接得到的湍流动量输送系数CMobs, n表示样本总数, 对应稳定和不稳定条件下分别为39和30。
从表 1中可以看出, 稳定条件下, Launiainen95方案误差最小, 其后依次为Wang02, Dyer74, B & H91和Louis82方案, Businger71方案的计算误差最为显著。Launiainen95方案和Wang02方案在计算中均采用了B & H91方案所给出的普适函数, 因而, 这一误差分析结果表明:稳定条件下, B & H91方案针对夜间稳定层结状况所提出的普适函数对于湍流动量输送系数有较好的计算效果; 同时, 在这一理查孙数范围内, Dyer74方案也能够较好的估算湍流动量输送系数; 应用Louis82方案计算时, 取热力粗糙度等于空气动力学粗糙度, 这和实际情况不符, 因而误差相对较大; 当理查孙数小于0.1时, Businger71方案计算的湍流动量输送系数存在显著误差。不稳定条件下, Dyer74方案的估算误差最小, Wang02方案其次, 随后是Louis82和Launiainen95方案, Businger71方案的估算误差最大, 这说明不稳定条件下, 当理查孙数绝对值小于0.2时, Dyer74方案对湍流动量输送系数的估算效果最好。
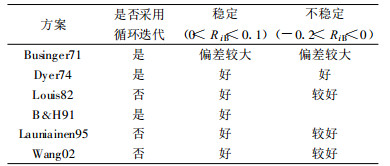
结合以上计算结果, 给出以上六种方案在稀疏短草下垫面状况下对湍流通量的的估算效果以及各方案的特性 (表 2)。
|
|
表 2 六种方案特性以及计算效果对比 Table 2 Contrast of the six parameterization schemes on characters and evaluation |
2 小结
通过对Businger71, Dyer74, Louis82, B & H91, Launiainen95以及Wang02这六种参数化方案的对比分析, 得到以下几点主要结论:
1) Businger71, Dyer74和B & H91方案依据普适函数通过循环迭代来计算湍流通量整体输送系数, 如直接应用于数值模式中, 需要耗费大量CPU计算时间。
2) 应用以上六种参数化方案计算得到的湍流动量输送系数之间存在较大差异, 且这种差异的大小受近地层稳定度和下垫面空气动力学粗糙度的影响十分显著。
3) 通过资料验证发现, 对于稀疏短草下垫面而言, 稳定条件下当理查孙数小于0.1时, 除Businger71方案存在显著低估以外, 其他各方案均能较好估算湍流动量输送系数。不稳定条件下当理查孙数绝对值小于0.2时, Dyer74方案对湍流通量整体输送系数的估算效果最好, 其次为Wang02, Launiainen95和Louis82方案, Businger71方案误差较大。
| [1] | Gao Z, Bian L G, Zhou X J, Measurements of turbulent transfer in the near-surface layer over a rice paddy in China. J Geophys Res, 2003, 108, (D13): 4387–4399. |
| [2] | 丁一汇. 地表通量的计算问题. 应用气象学报, 1997, 8, (1): 29–35. |
| [3] | European Centre for Medium-range Weather Forecasts. Proceedings of ECMWF Workshop on Parameterization of Fluxes over Land Surfaces.European Centre for Medium-range Weather Forecasts, Reading, England, 1988:1-392. |
| [4] | Garratt J R, Pielke R A, On the sensitivity of mesoscale models to surface-layer parameterization constants. Boundary-Layer Meteorol, 1989, 48: 377–387. DOI:10.1007/BF00123060 |
| [5] | Monin A S, Obukhov A M, Basic regularity in turbulent mixing in surface layer of the atmosphere. Akad Nauk SSSR Geofiz Inst, 1954, 24: 163–187. |
| [6] | Businger J A, Wyngaard J C, Izumi Y, et al. Flux-profile relationships in the atmospheric surface layer. J Atmos Sci, 1971, 28: 181–189. DOI:10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2 |
| [7] | Dyer A J, A review of flux-profile relationships. Boundary-Layer Meteorol, 1974, 7: 363–372. DOI:10.1007/BF00240838 |
| [8] | Louis J F, A parametric model of vertical eddy fluxes in the atmosphere. Boundary-Layer Meteorol, 1979, 17: 187–202. DOI:10.1007/BF00117978 |
| [9] | Louis J F, Tiedtke M, Geleyn J F.A Short History of the Operational PBL-parameterization at ECMWF.Workshop on Planetary Boundary Layer Parameterization, Shinfield Park, Reading, Berkshire, UK, European Centre for Medium Range Weather Forecasts, 1982:59-79. |
| [10] | Wang S P, Wang Q, Doyle J.Some Improvements to Louis Surface Parameterization.Paper Presented at 15th Symposium on Boundary Layers and Turbulence, Am Meteor Soc, Wageningen, Netherlands, 2002. |
| [11] | Miller M J, Beljaars A C M, Palmer T N, The sensitivity of the ECMWF model to the parameterization of evaporation from the tropical ocean. J Climate, 1992, 5: 418–434. DOI:10.1175/1520-0442(1992)005<0418:TSOTEM>2.0.CO;2 |
| [12] | Holtslag A A M, De Bruin H A R, Applied modeling of the nighttime surface engery balance over land. J App Meteorol, 1988, 27: 689–704. DOI:10.1175/1520-0450(1988)027<0689:AMOTNS>2.0.CO;2 |
| [13] | Beljaars A C M, Holtslag A A M, Flux parameterization over land surfaces for atmospheric models. J App Meteorol, 1991, 30: 327–341. DOI:10.1175/1520-0450(1991)030<0327:FPOLSF>2.0.CO;2 |
| [14] | Launiainen J, Derivation of the relationship between the Obukhov stability parameter and the bulk Richardson number for flux-profile studies. Boundary-Layer Meteorol, 1995, 76: 165–179. DOI:10.1007/BF00710895 |
| [15] | Gao Z, Chae N, Kim J, et al. Modeling of surface energy partitioning, surface temperature and soil wetness in the Tibetan prairie using the Simple Biosphere Model 2 (SiB2). J Geophys Res, 2004, 109: D06102. DOI:10.1029/2003JD004089 |
| [16] | Yang K, Koike T, Yang D, Surface flux parameterization in the Tibetan Plateau. Boundary-Layer Meteorol, 2003, 116: 245–262. |
 2007, 18 (3): 407-411
2007, 18 (3): 407-411