2. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
3. 陕西省气象台, 西安 710015;
4. 北京敏视达雷达有限公司, 北京 100085
2. National Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Shaanxi Meteorological Observatory, Xi'an 710015;
4. Beijing Metstar Radar Co Ltd, Beijing 100085
切变线在气象上是专指具有气旋式切变的风场不连续线, 为我国主要降水天气系统之一。而风场上气流聚合的不连续线, 称为辐合线[1]。天气系统中具有辐合线或切变线性质的很多, 如飑线、锋面等。辐合线或切变线上也常会出现强对流或其他天气现象。
风切变包括水平风的垂直切变, 水平风的水平切变以及垂直的风切变。许多研究和经验表明, 中低层的中尺度辐合线或切变线的建立对于暴雨的发生和落区具有很好的指示作用[2], 并且是强单体合并的动力因素。强对流过程的预报对交通、大型政治、体育等活动的气象保障有重要的意义。低空风切变还是造成飞行器在起飞或降落时发生事故的主要原因。对于龙卷、飑线等强对流云的发展和维持, 低层风的垂直切变也有很重要的作用[3-4]。
多普勒天气雷达是探测大气风场中尺度结构的重要手段。许多中尺度天气系统在多普勒径向风场信息中都有其独特的二维特征结构[5], 利用这些特征可以对其进行识别和追踪。这些识别和追踪技术的研究应用正是临近预报技术发展中的重要内容[6]。1982年美国JAWS (Joint Airport Weather Study) 研究报告中证明了多普勒雷达可探测微下击暴流[7]。Uyeda等和Hermes等在研究自动识别、追踪阵风锋的方法中指出, 当阵风锋与雷达径向不垂直时, 辐合区在多普勒雷达上的显示为速度沿径向减小的区域, 进而指出可以根据沿径向的最大速度梯度区确定阵风锋的位置[8-9]。
在切变线的识别方面, 国内外已经开展了一些研究。美国强风暴实验室研究出某些阈值以区别中气旋切变与其他切变[10]; Campbell等研制了WX1系统, 利用人工智能的方法实现对风切变的自动识别[11]。国内, 胡明宝等曾利用单多普勒雷达风场资料探测低空风切变[12]。
目前国内外有些雷达系统也已经提供了一些风切变产品, 可以得到沿不同方向 (径向、方位角、仰角) 的风切变场[13]。一般的算法是先对资料进行预处理, 用线性内插技术对缺测区进行填补, 然后再分别计算径向、方位角、仰角切变, 也可以两两组合成组合切变。这种方法对资料的预处理比较简单, 而且线性内插也可能干扰原来的风场结构, 最终影响切变的计算。另外, 这些产品仅提供风切变图, 不能实现对辐合与切变线的自动识别。
WSR-88D雷达产品中也有切变线识别产品, 具体算法是先沿径向选择一定数量的像素点, 对原始径向速度数据进行滑动平均, 这里只选择反射率超过一定阈值的相应数据, 然后再用这些值计算径向和切向切变, 最后将梯度值插值到笛卡儿坐标系上, 并进行滤波。这种算法对资料的预处理也是比较简单的, 没有考虑到缺测区域和回波边缘。而且最后的产品仅限于平面位置显示 (PPI), 缺少垂直切变。
本文介绍的就是在上述方法的基础上, 做了许多改进后, 利用多普勒天气雷达的径向速度来自动识别风切变线和辐合线, 显示垂直切变图, 为临近预报提供更有效的参考资料的方法。要注意的是, 这里识别的仅是径向速度的切变 (切向切变) 和辐合 (径向切变), 与真实风场的切变和辐合是不同的概念, 但有联系。
1 计算方法本文应用雷达径向速度的体扫资料, 所有步骤是在PPI、极坐标上实现的。
根据气象学原理, 辐合线定义为径向速度梯度最小区 (即速度减小率最大区)。切变线定义为径向速度的方向和大小沿方位角方向 (即切向) 有显著变化的区域。这里主要识别的是β-中尺度的切变线和辐合线。
1.1 资料预处理资料预处理的主要目的是减小径向速度噪声的同时有效保留径向速度的中尺度结构。具体步骤如下:①径向速度资料的中值滤波。对每个目标点, 选择周围n1×n2个像素点 (即分别沿切向和径向取n1和n2个点), 将这些值排序, 取中间值代替目标点的值; ②沿径向和切向的滑动平均。中值滤波后再分别沿径向和切向计算连续n3和n4个像素点的平均值, 来代替中间点的值。对于无径向速度资料区及其附近资料的处理方法是:不进行外插值处理, 只有达到一定有效资料数量后才进行处理, 否则将无资料区附近的点也作为无资料处理。这样避免了在回波边缘区域由于计算点数不够而造成的计算误差。因为缺测区域的孤立性和不连续性, 而切变线和辐合线一般都是连续和有一定长度的, 所以剔除这些区域并不会影响到最终的计算结果。
1.2 径向速度的径向和切向切变的计算采用最小二乘拟合法, 对任一组随机数据 (y1, x1), (y2, x2), ……, (yn, xn), 可以求得通过这些点的最适合直线, 并能计算出这条直线的斜率。这里计算的切变值都是根据此原理计算的。
径向速度的径向切变, 定义为雷达径向速度从原点开始沿某一径向随距离的变化, 即

|
(1) |
式 (1) 中, vi为第i个点的径向速度, ri为相应点距雷达的距离, n为参与计算的资料点数。这里所取的点应该在同一条径线上, 即方位角θ是常数。
径向速度的切向切变, 定义为在距雷达相同距离上的像素点上, 径向速度从0°方位角开始 (正北) 沿顺时针方向的变化, 即
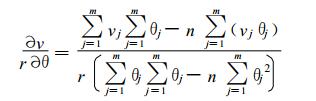
|
(2) |
式 (2) 中, vj为第j个点的径向速度, θj为相应的方位角, r为距雷达距离, m为参与计算的资料点数。这里所取的点应该距雷达距离相同, 即r为常数。
1.3 垂直切变的计算这里定义垂直切变为, 在相同方位角上, 距雷达距离相同 (即r, θ都是常数) 的上下两层PPI上径向速度值随垂直高度的变化, 即
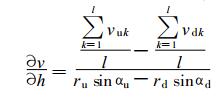
|
(3) |
式 (3) 中, vu, vd分别为相邻上下两层径向速度, 并进行了平滑拟合 (拟合区间为l); ru, rd分别为上、下层径向距离; αu, αd分别为上下两层PPI的仰角。计算时也是只当上下两层的数据同时有效时才进行, 否则作为无资料处理。最后为了显示更清楚, 可以再对计算结果进行中值滤波。
1.4 径向方位组合切变径向方位组合切变表示雷达径向速度沿径向、切向的综合变化, 定义为: 



本文应用了3个天气过程资料, 其中两个为S波段新一代天气雷达 (CINRAD/SA) 观测结果, 分别是2005年3月22日广州的一次强飑线天气过程和2004年6月21日济南的暴雨过程; 荆州C波段新一代天气雷达 (CINRAD/CC) 于2002年7月22—23日观测到的一次混合云暴雨天气过程。
CINRAD/SA雷达的最大可测半径为230 km, 库长为250 m, 低层相邻方位夹角为1.00°; CINRAD/CC雷达的最大可测半径为150 km, 库长为150 m, 低层相邻方位夹角为0.70°。
3 资料预处理的效果分析计算“窗口”大小 (即参与计算的资料点数n1, n2, n3, n4) 不同对预处理效果影响很大。沿切向的n1, n3都不可能取值过大, 这是因为随着径向距离的增加, 相邻方位角之间的距离会增加。为了尽量减小这种差别, 一般都取值为3。下面着重讨论当径向n2, n4变化时对预处理结果的影响。
这里采用沿径向速度变化比较大的一组数据为例做分析, 对于沿切向变化的分析情况和结果类似, 故略去。分析数据为2004年6月21日17:40(世界时, 下同) 济南CINRAD/SA雷达的观测资料。选取最低层 (0.53°仰角), 方位角为44.64°, 第120~240个像素点的径向速度数据。
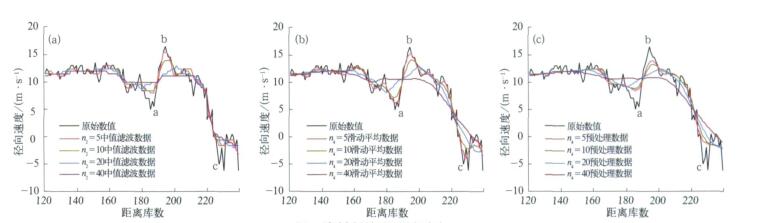
3.1 中值滤波分析令n2=5, 10, 20, 40对资料进行中值滤波, 将结果与原始资料对比, 见彩图 1a。图中原始资料存在明显的库间脉动, 经中值滤波后这种脉动基本消失, 但仅做这样的处理后数据曲线不够平滑。图中存在两处梯度大值区 (a—b段和b—c段)。在a—b段, n2=5和n2=10的滤波结果还能保持这个区域的大梯度值, n2=20的滤波结果中梯度明显减小, n2=40时几乎消失; 在b—c段, 这4个滤波结果的大梯度区几乎重合, 保持了这个区间的大梯度特征。可见, 对较大尺度的大梯度区域, 选择合适的滤波参数, 可以实现去除资料脉动的同时保持大梯度值不变。
|
|
| 图 1. 资料预处理效果对比 (a)中值滤波效果对比,(b)滑动平均效果对比,(c)中值滤波后滑动效果对比 Fig 1. Contrast of data pretreatment (a) contrast of media filtering, (b) contrast of moving average, (c) contrast of media filtering first and then moving average | |
3.2 滑动平均分析
令n4=5, 10, 20, 40作径向滑动平均, 与原始数据对比, 结果见彩图 1b。图中n4取值较小时大的梯度区间可以保持, 但库间脉动仍然存在, 没有中值滤波的效果好; 随着n4的增加, 库间脉动去除的同时, 大梯度区却逐渐减小。说明单纯的滑动平均不能实现在去除库间脉动的同时保留需要的中尺度结构。
3.3 中值滤波后滑动平均分析对原始资料先进行中值滤波 (3×10), 然后令n4=5, 10, 20, 40作径向滑动平均, 与原始数据对比, 结果见彩图 1c。图中n4较小时 (即n4=5, 10, 20时) 的3个处理结果相似, 综合了单纯中值滤波和滑动平均的优点, 基本能做到在对库间脉动过滤的同时保留了整体中尺度结构, 并且数据是光滑连续的。但需要注意平滑尺度过大时, 也会对中尺度结构产生一些影响。
4 切变计算分析切变计算后为了突出识别结果, 一般要设置一定的显示阈值, 只保留切变值最大区域。
切变计算时参与计算的资料点数 (n) 不同, 意味着识别的切变尺度不同。彩图 2a~c中, 无论n值大小, 大切变值都是散乱的, 不能清晰表现出速度图上的辐合区。说明直接用原始数据计算速度切变来实现对辐合区的识别比较困难。彩图 2d~f中, 辐合区识别结果清晰明确, 与速度图上直观可见的辐合区位置基本吻合。径向切变值随着n值的增大而减小, 这是因为n值增加, 计算的空间尺度增加造成的。n值过小, 计算结果会受到预处理后残存的“噪声”影响; n值过大, 可能将某些大切变区“漏掉”。可见, 只有选择合适的切变计算尺度才能得到较好的识别效果。

|
|
| 图 2. 2004年6月21日17:40济南多普勒天气雷达0.53°仰角速度图计算结果 (a)~(c)用原始径向速度计算径向切变(显示阈值:2.5m·s-1·km-1)n=10(a), n=20(b), n=40(c), (d)~(f)用预处理后数据计算的径向切变(显示阈值:1.5 m·s-1·km-1)n=10(d), n=20(e), n=40(f) Fig 2. Radial shear of elevation 0.53° in Jinan at 17:40 on June 21, 2004 (a)-(c) radial shear calculated with original data (show gate:2.5 m·s-1·km-1) n=10(a), n=20(b), n=40(c), (d)-(f) radial shear calculated with pretreated data (show gate:1.5 m·s-1·km-1) n=10(d), n=20(e), n=40(f) | |
另外, 预处理尺度的不同也影响到切变计算时n值的选择。选取不同的n1, n2, n3, n4进行预处理, 再选择不同的n值区间计算切变, 对比发现:预处理尺度与切变计算尺度均较大或较小时识别结果不好; 预处理尺度大而切变计算尺度较小时的识别结果与预处理尺度小、切变计算尺度较大的结果相近; 当两个尺度均与要识别的辐合区比较一致时得到的识别效果较好。
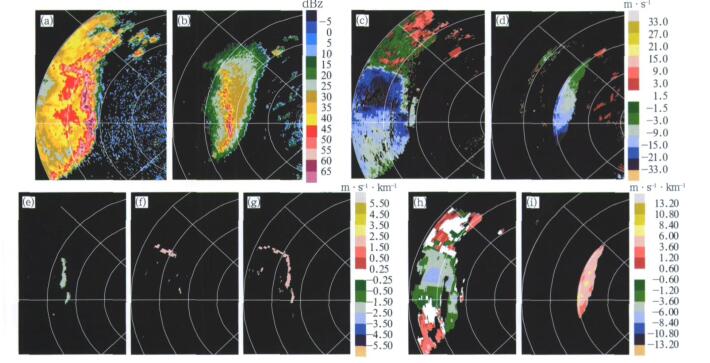
5 识别结果分析 5.1 飑线过程分析2005年3月22日广州发生一次强飑线天气过程 (彩图 3)。在0.53°仰角的图中, 飑线位于雷达西侧160 km处, 这一区域反射率因子最大 (45~60 dBz), 在其后部出现负的垂直切变最大值。径向、切向、组合切变的最大值都出现在飑线的前沿, 这可能与飑线后部存在较强的入流有关, 一般在低空急流最大风速中心前方会有明显的水汽和质量辐合, 有利于新对流单体在这一区域生成[14]。
|
|
| 图 3. 2005年3月22日01:32广州飑线过程多普勒大气雷达回波及切变识別结果 (a) 0.53°仰角反射率因子,(b) 2.5°仰角反射率因子,(c)0.53°仰角径向速度, (d) 2.5°仰角径向速度, (e)0.53°仰角径向切变(显示阈值:1.2 m·s-1·km-1,(f) 0.53°仰角切向切变(显示阈值:1.5 m·s-1·km-1), (g) 0.53°仰角组合切变(显示阈值:1.7 m·s-1·km-1), (h) 0.53°和1.49°仰角间垂直切变,(i) 2.5°和3.5°仰角间垂直切变 Fig 3. Doppler radar echo and detecting result of a squall line in Guangzhou at 01:32 on March 22, 2005 (a) reflectivity in elevation 0.53°, (b) reflectivity in elevation 2.5°, (c) velocity in elevation 0.53°, (d) velocity in elevation 2.5°, (e) radial shear in elevation 0.53° (show gate: 1.2 m·s-1·km-1), (f) azimuthal shear in elevation 0.53° (show gate:l.5 m·s-1·km-1), (g) combined shear in elevation 0.53° (show gate: 1.7 m·s-1·km-1), (h) vertical shear between elevation 0.53° and 1.49°, (i) vertical shear between elevation 2.5° and 3.5° | |
将2.5°仰角与0.53°仰角图对比发现, 飑线距雷达的水平距离没有变化; 在低层飑线后部存在负垂直切变; 高层飑线前面出现正垂直切变。说明飑线在低层后部和高层前部都存在与飑线移动方向相同的径向速度, 并且由低至高逐渐减弱后又逐渐加强, 这可能是低层入流与高层出流配置的结果。中层飑线内部是强烈的垂直上升气流, 所以垂直切变比较弱 (图略)。这样的识别结果与Houze等1989年提出的中纬度飑线概念模式是基本一致的, 与中纬度飑线内部结构的理论是吻合的[15]。
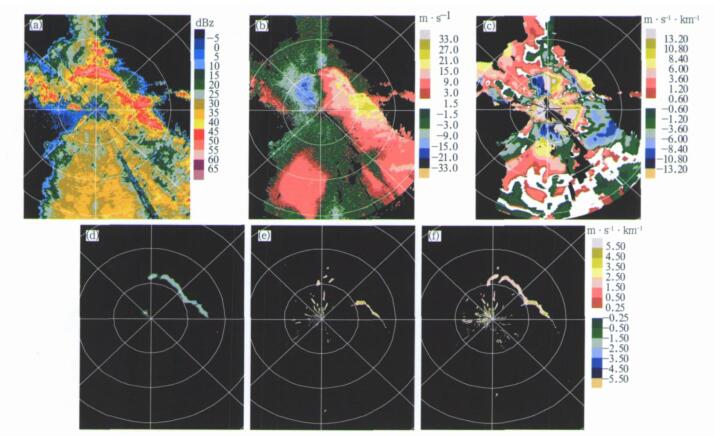
2004年6月21日在济南观测到一次带状强降水回波 (彩图 4)。图中强降水区的反射率因子为40~50 dBz, 辐合线位置位于带状回波前沿, 降水区前部出现正的垂直切变最大值 (大于6.0 m·s-1·km-1), 后部为负垂直切变 (靠近雷达附近上下两层间的高度较小所以垂直切变很大)。在1.49°仰角回波图上 (图略), 切变线前部出现正径向速度区, 后部正径向速度减弱, 与彩图 4c中切变线前后径向速度的垂直变化是一致的。带状回波的位置没有变化, 强度略减弱, 相应的切变线识别结果也不连续且强度减弱。
|
|
| 图 4. 2004年6月21日17:34济南带状强回波降水多普勒天气雷达回波及切变识别结果 (a)0.53°仰角反射率因子,(b)0.53°仰角径向速度,(c) 0.53°仰角和0.49°仰角间垂直切变, (d) 0.53°仰角径向切变(显示阈值:1.2 m·s-1·km-1), (e)0.53°仰角切向切变(显示阈值:1.7 m·s-1·km-1),(f)0.53°仰角组合切变(显示阈值:1.7 m·s-1·km-1) Fig 4. Doppler radar echo and detecting result of a strong convective line at 17:34 on June 21, 2004 (a) reflectivity in elevation 0.53°, (b) velocity in elevation 0.53°, (c) vertical shear between elevation 0.53° and 1.49°, (d) radial shear in elevation 0.53° (show gate:1.2 m·s-1·km-1), (e) azimuthal shear in elevation 0.53° (show gate:l.7 m·s-1·km-1), (f) combined shear in elevation 0.53° (show gate:1.7 m·s-1·km-1) | |
5.2 混合云暴雨过程分析
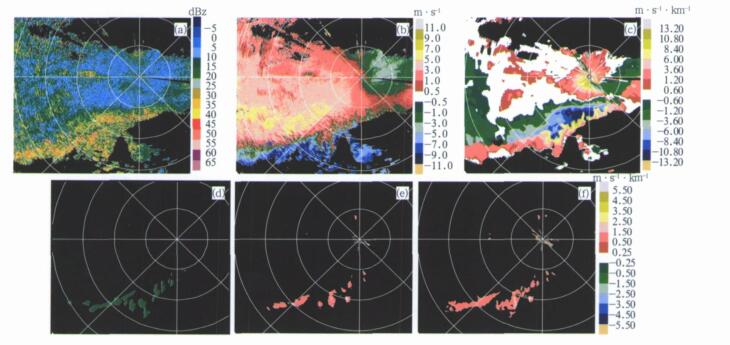
2002年7月22日荆州发生了一次与中尺度切变线有关 (彩图 5) 混合云暴雨天气过程。强降水区域的反射率因子为25~40 dBz, 比前两个过程明显减小, 径向、切向和组合切变最大值也相应减小, 但位置仍与强降水区一致。在切变线的北侧和南侧分别出现负垂直切变和正垂直切变, 说明上层正径向速度减弱, 负径向速度加强, 切变线向北移动。
|
|
| 图 5. 2002年7月22日11:49荆州混合云暴雨过程多普勒天气雷达回波及切变识别结果 (a) 0.6°仰角反射率因子,(b)0.6°仰角径向速度,(c)0.6°和1.4°仰角间垂直切变,(d) 0.6°仰角径向切变(显示阈值:0.5 m·s-1·km-1), (e) 0.6°仰角切向切变(显示阈值:0.8 m·s-1·km-1), (f)0.6°仰角组合切变(显示阈值:0.8 m·s-1·km-1) Fig 5. Doppler radar echo and detecting result of a mixing cloud in Jinzhou at 1l:49 on July 22, 2002 (a) reflectivity in elevation 0.6°, (b) velocity in elevation 0.6°, (c) vertical shear between elevation 0.6° and 1.4°, (d) radial shear in elevation 0.6° (show gate:0.5 m·s-1·km-1), (e) azimuthal shear in elevation 0.6° (show gate:0.8 m·s-1·km-1), (f) combined shear in elevation 0.6* (show gate:0.8 m·s-1·km-1) | |
与同一时次其他仰角资料对比发现, 降水区和切变线系统均随高度向北倾斜, 每层识别出的切变线的北侧和南侧都分别出现负垂直切变和正垂直切变。说明垂直切变的计算结果与实际径向风场随高度的变化是一致的, 而径向风场的高低层配置导致了整个系统的空间位置变化。
6 总结本文研究了利用多普勒雷达径向速度资料识别风切变和辐合线的方法, 并利用3个强降水个例资料分析了雷达径向速度资料预处理和风切变线、辐合线的识别效果。结果表明:
1) SA雷达和CC雷达原始径向速度资料存在明显的库间脉动; 一定库间尺度的滤波和平滑可有效消除径向速度的脉动变化, 保留径向速度的中尺度信息。
2) 资料预处理后, 选择合适的计算“窗口”, 利用最小二乘拟合方法可以很好提取径向速度沿径向和切向切变, 识别结果与径向速度分布图中反映的切变、辐合信息比较一致。
3) 不同降水过程切变显示阈值不同, 径向速度水平切变强弱与降水强度具有一定的正相关性, 垂直切变能够提供径向风场的高低层配置信息。
4) 利用径向速度资料可以实现对风切变和辐合线的自动识别, 为灾害性天气的预警、预报提供重要的客观依据。
需要指出的是, 关于算法中显示阈值的设定, 需要针对各地情况, 对更多的天气个例进行试验、分类、总结, 才能得到最优的识别结果。
| [1] | 朱炳海, 王鹏飞, 束家鑫. 气象学词典. 上海: 上海辞书出版社, 1985: 96-97. |
| [2] | 张家国, 吴翠红, 王珏, 等. 一次冷锋大暴雨过程的多普勒雷达观测分析. 应用气象学报, 2006, 17, (2): 226–231. |
| [3] | 何彩芬, 姚秀萍, 胡春蕾, 等. 一次台风前部龙卷的多普勒天气雷达分析. 应用气象学报, 2006, 17, (3): 370–375. |
| [4] | 姚建群, 戴建华, 姚祖庆. 一次强飑线的成因及维持和加强机制分析. 应用气象学报, 2005, 16, (6): 746–753. |
| [5] | 陶祖钰, 曾立新. 中尺度系统的模拟Doppler图像. 应用气象学报, 1993, 4, (1): 8–15. |
| [6] | 陈明轩, 俞小鼎, 谭晓光, 等. 对流天气临近预报技术的发展与研究进展. 应用气象学报, 2004, 15, (6): 754–766. |
| [7] | Wilson J W, Roberts R D, Kessinger C, et al. Microburst wind structure and evaluation of Doppler radar for airport wind shear detection. J Appl Meteor, 1984, 23: 898–915. DOI:10.1175/1520-0450(1984)023<0898:MWSAEO>2.0.CO;2 |
| [8] | Uyeda H, Zrnić D S, Automatic detection of gust fronts. J Atmos Oceanic Technol, 1986, 3: 36–50. DOI:10.1175/1520-0426(1986)003<0036:ADOGF>2.0.CO;2 |
| [9] | Hermes L G, Witt A, Smith S D, et al. The gust-front detection and wind-shift algorithms for the terminal Doppler weather radar system. J Atmos Oceanic Technol, 1993, 10: 693–708. DOI:10.1175/1520-0426(1993)010<0693:TGFDAW>2.0.CO;2 |
| [10] | Zrnić D S, Burgess D W, Hennington L D, Automatic detection of mesocyclonic shear with Doppler radar. J Atmos Oceanic Technol, 1985, 2: 425–438. DOI:10.1175/1520-0426(1985)002<0425:ADOMSW>2.0.CO;2 |
| [11] | Campbell S D, Olson S H, Recognizing low-altitude wind shear hazards from Doppler weather radar:An artificial intelligence approach. J Atmos Oceanic Technol, 1987, 4: 5–18. DOI:10.1175/1520-0426(1987)004<0005:RLAWSH>2.0.CO;2 |
| [12] | 胡明宝, 谈曙青, 汤达章, 等. 单部多卜勒雷达探测低空风切变方法. 南京气象学院学报, 2000, 23, (1): 113–118. |
| [13] | 中国人民解放军总参谋部气象局. 多普勒天气雷达资料分析与应用. 北京: 解放军出版社, 2000: 150-159. |
| [14] | 陆汉城, 杨国祥. 中尺度天气原理和预报. 北京: 气象出版社, 2004: 106-114. |
| [15] | 张玉玲. 中尺度大气动力学引论. 北京: 气象出版社, 1999: 147-176. |
 2007, 18 (3): 314-320
2007, 18 (3): 314-320

