2. 南京信息工程大学, 南京 210044;
3. 重庆市气象局, 重庆 401147;
4. 水利部淮河水利委员会水文局, 蚌埠 233001
2. Nanjing University of Information Science & Technology, Nanjing 210044;
3. Chongqing Municipal Meteorological Bureau, Chongqing 401147;
4. Bureau of Hydrology, Huaihe River Commission, Ministry of Water Resources PRC, Bengbu 233001
与面积较大或地形平坦的流域相比, 几十到几百平方公里大小的山区流域对降水的响应要快得多, 其径流预报对实时降水测量的要求也相应较高。目前, 美国的WSR-88D以及我国的CIN RAD以及其他国家的一些雷达都已采用6 min左右一次体积扫描方案, 有利于雷达定量测量降水精度的提高[1]及降水测量结果在水文气象中的应用[2]。中国气象局与水利部合作的“淮河黄河流域暴雨洪水监测预报系统试验”项目 (以下简称“黄淮试验”项目) 在淮河南岸的淠河流域布设了加密雨量站网, 该流域位于大别山北麓, 距离合肥CINRAD/SA雷达站75~175 km。本文利用“黄淮试验”项目中气象部门提供的合肥CINRAD/SA雷达体扫原始数据资料和淮河水利委员会提供的2003年6月20日至7月12日的加密雨量站资料、佛子岭流域出口流量资料、蒸发资料, 同时结合1:250000 DEM (Digital Elevation Model) 数字高程模型资料进行数字流域划分, 作为TOPMODEL降水-径流模型的输入, 研究将雨量计测量值和雷达测量降水用于山区流域径流模拟时的一些特性。
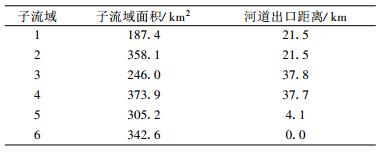
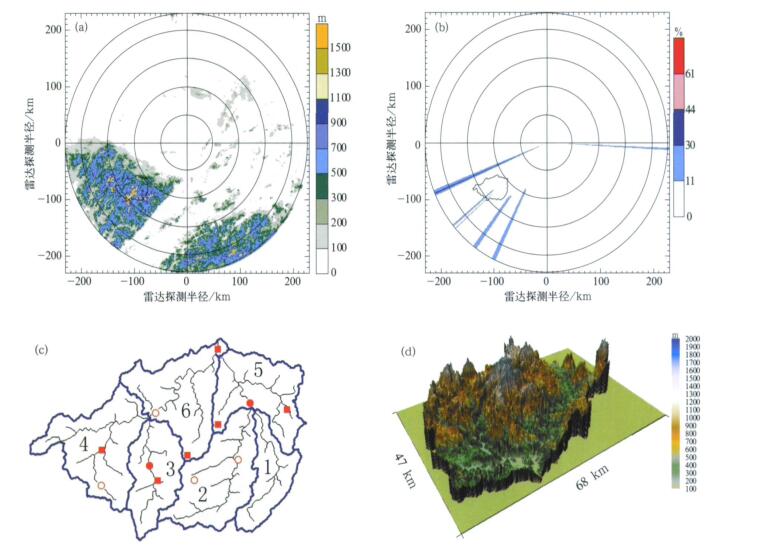
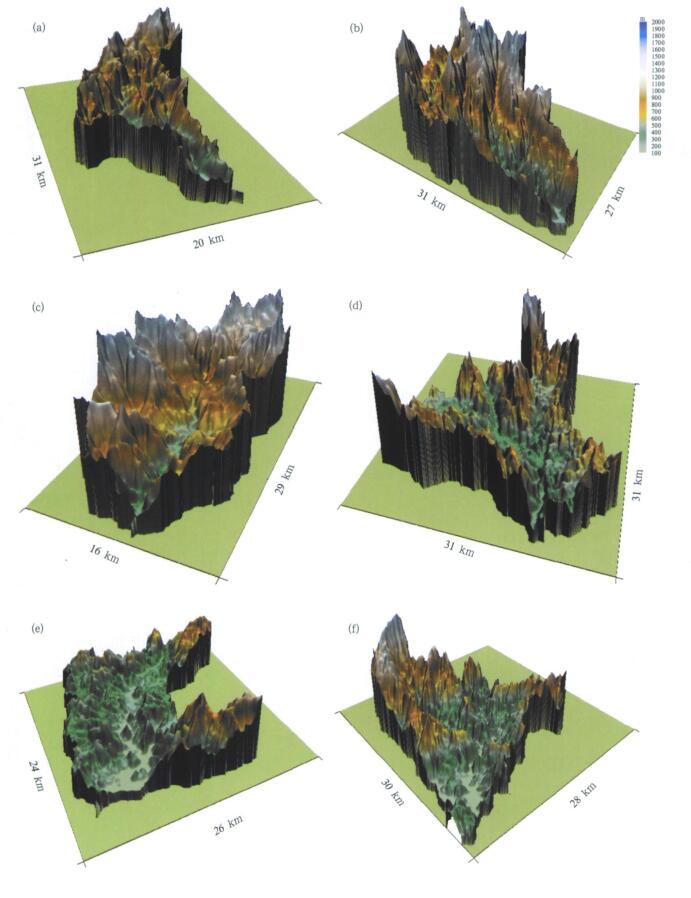
1 研究区域淠史杭灌区由淠河、史河、杭埠河3个毗邻灌区组成, 是我国著名的特大型灌区之一。淠河灌区以淠河上游的佛子岭、磨子潭、响洪甸3座大型水库为水源, 渠首枢纽工程位于水库下游的六安市横排头。淠河横排头以上为山区, 横排头站坝上集水面积4370 km2, 其中响洪甸、佛子岭水库以上面积为3240 km2, 两大水库与横排头区间集水面积为1130 km2。由于本文所用DEM资料的分辨率在进行数字流域划分时只能划分出响洪甸流域和佛子岭流域, 而响洪甸流域波束阻挡较为严重, 因此, 本文以佛子岭水库控制的流域作为研究区域。彩图 1为研究区域示意图, 其中彩图 1a为合肥雷达周围地形图以及佛子岭流域的位置, 彩图 1b为合肥雷达0.5°仰角上阻塞率以及佛子岭流域的位置, 彩图 1c为佛子岭流域6个子流域划分示意图及雨量计分布图, 流域总面积为1813 km2, 彩图 1d为佛子岭流域三维视图。由于采用1:250000 DEM资料, 因此各仰角波束阻挡程度的计算可较一般的等射束高度图法[3]更为精细, 本文算法与Kucera等[4]的算法类似。同时, 数字流域的划分采用自然子流域划分法, 用数字高程流域水系模型DEDNM (Digital Elevation Drainage Network Model)[5], 又称TOPAZ (Topographic PArameteriZation)[6]作为数字地形分析工具进行流域河网水系识别和子流域分割。除子流域5和子流域6外, 其余为闭合子流域。表 1为佛子岭流域中各子流域的面积和河道出口距离, 各子流域河道出口距离指子流域出口到佛子岭流域出口的距离。彩图 2为佛子岭流域中6个子流域的三维视图。
|
|
| 图 1. 研究区域示意图(a)合肥雷达周围地形图以及佛子岭流域的位置,(b)合肥雷达仰角0.5°上阻塞率以及佛子岭流域的位置,(c)基于1:250000 DEM的佛子岭流域6个子流域划分示意图及雨量计分布图(实心方块表示评估站,实心圆和空心圆表示校准站),(d)佛子岭流域三维视图 Fig 1. Presentation of the study area (a) relief map of the Hefei radar and the location of Foziling basin, (b) beam blockage of Hefei radar at elevation of 0.5° and location of the Foziling basin, (c) a sketch map of the 6 subcatchments of the Foziling basin from 1:250000 DEM and the location of the rain gauge network (solid squares for evaluation and circles for adjustment), (d) the 3D view of the Foziling basin | |
|
|
表 1 佛子岭流域中各子流域的面积和河道出口距离 Table 1 List of the subcatchments with their corresponding area and distance to the outlet of the Foziling basin |
|
|
| 图 2. 佛子岭流域中6个子流域的三维视图 (a)子流域1,(b)子流域2,(c)子流域3,(d)子流域4,(e)子流域5,(f)子流域6 Fig 2. The 3D views of 6 subcatchments in the Foziling basin (a) subcatchment 1, (b) subcatchment 2, (c) subcatchment 3, (d) subcatchment 4, (e) subcatchment 5, (f) subcatchment 6 | |
2 降水测量精度评估
水文上往往基于地面雨量计测值进行面雨量计算, 如泰森多边形法[7]是基于雨量计位置和雨量计之间的距离将流域划分为多个多边形, 围绕某一雨量计的多边形面积与流域总面积之比就是该雨量计测值在流域面雨量中所占的权重。又如距离平方反比法是将流域分成若干格点, 格点上的降雨量用邻近各雨量站的雨量资料作加权平均得到, 权重因子为格点到各雨量站距离平方的倒数, 雨量站到格点的距离d越近, 其权重1/d2也越大。流域面雨量可从各格点的降雨量得出。虽然泰森多边形法应用较广, 但其缺点是把各雨量站所控制的面积在不同的降雨过程中都视作固定不变, 与实际情况不符。因此, 本文将需要进行面雨量计算的流域分成1 km×1 km大小的格点, 用距离平方反比法计算每个格点上的降水量, 流域上所有格点降水量之和除以流域面积, 就得到流域面雨量。这样也有利于对格点上的降水测量精度进行评估。
另一方面, 天气雷达在流域面雨量计算中的应用也越来越广泛[8-11]。刘晓阳等[9]将史灌河流域的子集水区———梅山水库集水区 (1966 km2) 划分为6个子集水区后, 运用TOPMODEL模拟各子集水区产流, 进而演算梅山水库入库流量。研究表明, 在对流域进行分区后得到的模拟结果中, 得到一个分区前的模拟结果未能反映出的小洪峰, 该小洪峰是由小范围的短时强降水引起, 但除该处小洪峰外, 其余模拟结果在分区前后相差不大。考虑到本文中的佛子岭流域和刘晓阳等[9]研究的梅山水库集水区的面积均较大, 本文将研究佛子岭流域中面积较小的各子流域中的径流模拟, 探讨小流域径流与降水的一些关系。
本章主要对雨量计测量降水和雷达联合雨量计测量降水的精度进行评估, 流域径流模拟的结果见本文第3章。
彩图 1c为佛子岭流域雨量计分布图, 共有12个雨量计, 其中实心方块表示用于评估的6个雨量计 (以下简称评估站), 实心圆和空心圆表示用于雨量计测量面降水和雷达联合雨量计校准的6个雨量计 (以下简称校准站), 实心圆表示只用2个雨量计进行面雨量计算或雷达校准时所选用的雨量计。本文所用的雨量计资料为小时雨量资料, 时段为2003年6月20日01:00(世界时, 下同) 至7月12日00:00, 相应时段的雷达资料为合肥CINRAD/SA雷达体扫原始数据资料, 扫描方式为VCP11, 体扫间隔时间为6 min左右。资料预处理算法与WSR-88D降水处理子系统中的预处理算法类似[12], 将经过资料预处理后得到的复合扫描图用WSR-88D的缺省Z-I关系, 即
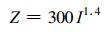
|
(1) |
转换为瞬时雨量图, 累加后可得校准前的雷达1 h累积降水量。
雷达定量测量降水有多种方法[1, 8-17]。本文在进行雷达-雨量计联合校准时采用平均校准法[17], 首先计算出某一时次雨量计测量的降水和雷达测量的降水之间的平均校准因子:
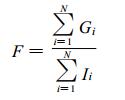
|
(2) |
式 (2) 中, N为用于校准的雨量计数, G代表雨量计观测到的小时雨量, I代表雨量计周围9个像素点 (这里每个像素点代表 1 km2) 雷达反演小时降水的平均值。将平均校准因子乘以雷达反演的小时降水场, 就得到平均校准后的雷达反演小时降水场。在进行雷达-雨量计联合校准时, 若用6个雨量计进行校准, 则当这6个雨量计中至少有2个的小时雨量测值达到1 mm以上时才进行校准, 若用2个雨量计进行校准, 则当这2个雨量计中至少有1个小时雨量测值达到1 mm以上时才进行校准。
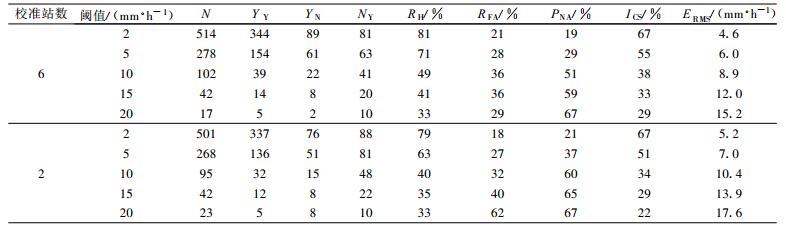
以6个评估站的小时雨量测值 (以下简称评估值) 作为评估标准。一方面对采用校准站测值时得到的与评估站对应的格点周围9点平均的小时雨量值 (以下简称雨量计测值) 进行评估, 格点上雨量的计算采用距离平方反比法。另一方面对雷达联合雨量计得到的评估站上空9点的平均值 (以下简称雷达测值) 进行评估。假定评估值与雨量计 (或雷达) 测值同时达到给定阈值的数目为YY, 评估值未达到阈值而雨量计 (或雷达) 测值达到阈值的数目为YN, 评估值达到阈值而雨量计 (或雷达) 测值未达到阈值的数目为NY, 本文采用以下指标对雨量计 (或雷达) 测值进行评估[18]:
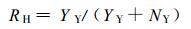
|
(3) |
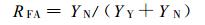
|
(4) |
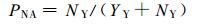
|
(5) |
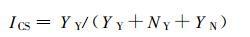
|
(6) |
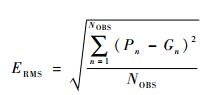
|
(7) |
式 (3)~(7) 中, RH (Hit Rate) 为命中率, 指发生的事件中被正确预报的比率, RFA (False Alarm Rate) 为虚警率, 指没有出现的事件被误报为出现, PNA (No Alarm Probability) 为漏报率, 指出现的事件被误报为未出现, ICS (Critical Success Index) 为临界成功指数, 指在有雨情况下预报的成功率, ERMS (Root Mean Squared Error) 为均方根误差, 用于了解测值与评估值的离散程度, 其值愈小离散程度愈小。式 (7) 中, NOBS为评估值达到给定阈值的总数目, Pn是对应点雨量计 (或雷达) 测值, Gn是某评估雨量计观测的小时降水量。
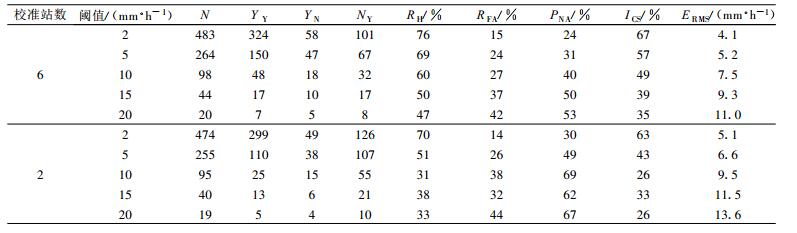
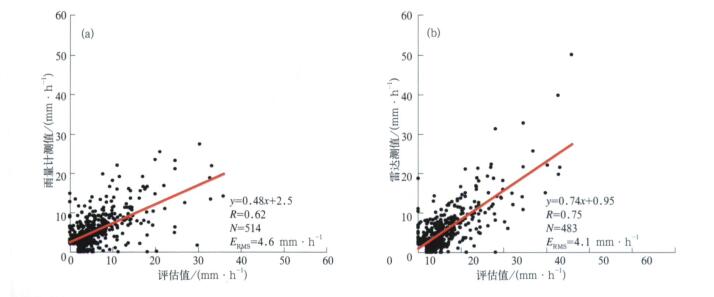
表 2和表 3分别为雨量计测值精度评估表和雷达测值精度评估表。表中N=YY +YN +NY, 统计时段为2003年6月20日01:00至7月12日00:00。由表 2和表 3可见, 雷达测值的精度是否高于雨量计测值的精度, 在一定程度上取决于用于校准的地面雨量计数目。若采用6个校准站, 当阈值取10 mm·h-1及更大时, 雷达测值的精度明显高于雨量计测值的精度, 当阈值取2 mm·h-1和5 mm·h-1时两者的差别不大。若采用2个校准站, 当阈值取20 mm·h-1时, 雷达测值的精度稍高于雨量计测值, 当阈值取15 mm·h-1时, 两者的精度接近, 当阈值取10 mm·h-1及更小时, 雷达测值的精度低于雨量计测值的精度。彩图 3为雨量计和雷达测值达到2 mm·h-1或评估值达到2 mm·h-1时雨量计 (彩图 3a) 和雷达 (彩图 3b) 测值与评估值比较散点图, 此时校准站为6站。由彩图 3及表 2和表 3可见, 从相关系数和临界成功指数以及均方根误差看, 雷达测量降水精度高于单独用地面雨量计计算的精度。
|
|
表 2 雨量计测值精度评估表 Table 2 Evaluation of the hourly precipitation calculated from the rain gauge data |
|
|
表 3 雷达测值精度评估表 Table 3 Evaluation of the accumulated hourly precipitation derived from the radar data |
|
|
| 图 3. 雨量计(a)及雷达(b)测值与评估值比较散点图 (图中给出了回归线、相关系数R、雨量测值个数N及均方根误差ERMS) Fig 3. Scatterplots of the hourly precipitation calculated from the rain gauge data (a) and the radar data (b) (the regression line, correlation coeffecient R between compared quangtites, the number of calculated rainfall values N, and the root mean squared error ERMS are also given in each plot) | |
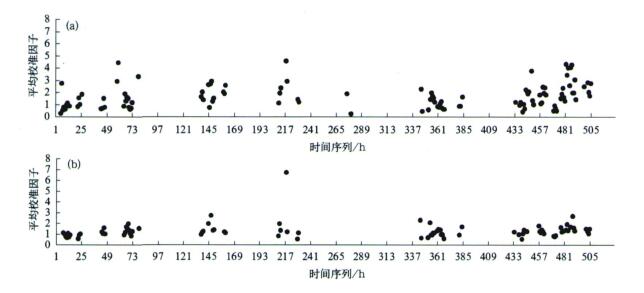
采用2个校准站时雷达测值精度降低的原因可能是采用2个校准站与采用6个校准站时各时次平均校准因子的差别。图 4为校准因子随时间的变化, 图 4a和图 4b分别用6个雨量计和2个雨量计进行校准, 没有校准因子的时段表示在该时段内没有计算校准因子。图 4a中平均校准因子的平均值为1.65, 图 4b中平均校准因子的平均值为1.29, 可见, 图 4a和图 4b中平均校准因子的差别较大。一般而言, 当雷达工作状态稳定时, 参加校准的雨量计越多, 校准因子越稳定。图 4中两个雨量计时的校准因子的变化明显小于6个雨量计时校准因子的变化, 这有可能是因为人为选取的这两个雨量计校准站缺乏代表性, 导致精度降低。因此, 参加校准的雨量计数目和代表性都很重要。
|
|
| 图 4. 2003年6月20日至7月12日平均校准因子随时间变化 (a)6个雨量计参加校准, (b)2个雨量计参加校准 Fig 4. Temporal variations of the averaged adjustment factors from June 20 to July 12, 2003 (a)6 rain gauges for adjustment, (b)2 rain gauges for adjustment | |
3 流域径流模拟
TOPMODEL降水-径流模型是由英国里兹大学于20世纪70年代开发[19], 并不断得到发展和完善的半分布式流域水文模型[20-22], 在我国也有广泛的应用[9, 11, 23-25]。变动产流面积概念是TOPMODEL的理论基础, 即饱和地表面积上形成的径流有两种方式:饱和坡面流和壤中流。饱和坡面流是在土壤水力传导性差、坡面平缓、坡形辐合的饱和坡面上形成的。饱和坡面流包括饱和地表面上的直接径流与回归流。近表层土壤水力传导度大以及坡面重力梯度大时则形成壤中流。TOPMODEL认为, 流域水文响应的分布特性可以通过地形分布特征 (地形指数) 来描述, 从而可以预测集水区土壤缺水量分布。该模型适合处理较小流域。其基本方程为[9]:
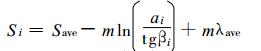
|
(8) |
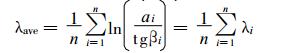
|
(9) |
式 (8)~(9) 中, Si为点i处的局地饱和缺水量, Save为流域平均饱和缺水量, λi为地形指数, n为流域格点数, m为土壤饱和水力传导度随土壤深度的衰减率, ai为点i以上坡面汇水面积, tgβi为点i处的地表坡度。
模型的5个输入参数为:土壤饱和水力传导度随土壤深度的衰减率m、地表土壤饱和导水率T0的自然对数值ln (T0)(单位:m2/h)、根系层的最大蓄水量Rmax (单位:m)、根系层的初始缺水量Rinit (单位:m) 和流域内部表面流的汇流速度V (单位: m/h)。TOPMODEL还要求输入所研究流域的面积距离函数和地形指数分布, 这些资料可由DEM数据计算。最后, 将雨量计资料计算得到的面雨量或雷达联合雨量计测量的面雨量、佛子岭流域出口流量、蒸发资料运用到TOPMODEL, 就可以进行佛子岭水库的入库流量模拟。由于只有整个佛子岭水库入库流量资料, 为了研究每个子流域的径流模拟情况, 本文对TOPMODEL网站提供的9502版的FORTRAN源程序TMOD9502.for进行了改写。TMOD9502可以最多输入10个子流域的地形指数分布、距离面积分布、河道出口距离, 计算产流, 然后汇流演算到流域出口断面, 因此, 与9701 Windows版相比, 该程序考虑了不同子流域的地形指数等因素。但该程序的降水输入和蒸散发输入仍然是使用全流域的面雨量和蒸散发量。本文将降水输入改为按每个子流域的面降水输入, 蒸散发仍然使用全流域的蒸散发量。这样, 通过以实测的佛子岭流域出口流量为标准对模拟的佛子岭流域出口流量进行率定后, 可以对该程序运行过程中输出的各子流域的径流深或流域出口流量时间序列进行比较研究。
模型率定的目标函数采用Nash-Sutcliffe模型效率系数E[26]:
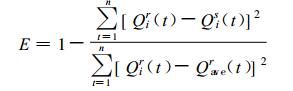
|
(10) |
式 (10) 中, Qir是第i个小时的参考流量, 用于模型率定时指实测入库流量, Qis是模型模拟的流量, Qaver为参考流量的平均值, n为时间序列长度。E以1为最佳。
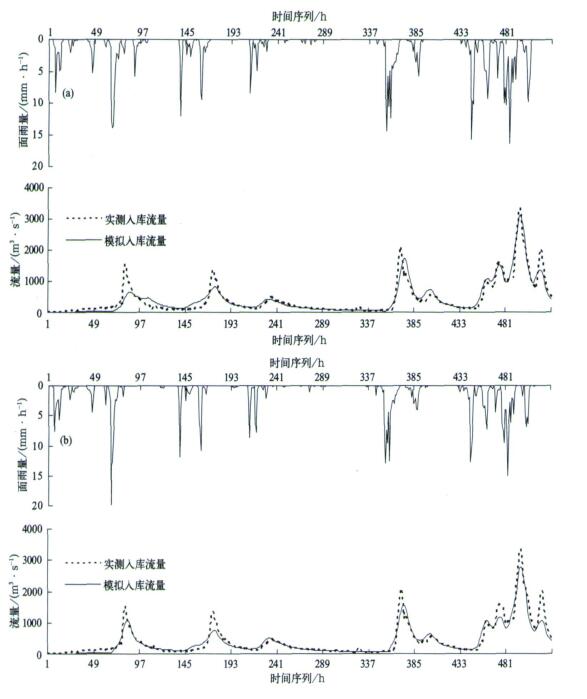
表 4为不同降水输入情况下佛子岭流域出口流量模拟的模型效率系数, 其中不考虑降水分布指将整个佛子岭流域的面雨量作为水文模型的降水输入, 考虑降水分布指按每个子流域的面降水进行降水输入。6个雨量计测值作为降水输入时的模型参数为:m=0.02, ln (T0)=5, Rmax=0.05, Rinit=0, V=4600;6站校准雷达测值作为降水输入时的模型参数为:m=0.02, ln (T0)=5, Rmax=0.05, Rinit=0.005, V=4700。图 5为2003年6月20日01:00到7月12日00:00佛子岭水库入库流量过程。由表 4可见, 在地面雨量计数目相同、都采用雨量计 (或雷达) 测值的条件下, 考虑降水分布的模拟效果总是好于不考虑降水分布的模拟效果; 当采用6个雨量计时, 雷达测值的模拟效果好于雨量计测值的模拟效果; 当采用2个雨量计并对模型参数重新率定后, 雷达测值的模拟效果比雨量计测值的模拟效果差。
|
|
表 4 不同降水输入情况下佛子岭流域出口流量模拟的模型效率系数 (E) Table 4 Coefficient of efficiency (E) of hydrographs simulated using rain gages and radar estimates for the Foziling basin |
|
|
| 图 5. 2003年6月20日01:00到7月12日00:00佛子岭水库实测和模拟入库流量过程 (a) 降水输入为6个雨量计计算的各子流域面雨量 (上部为相应的佛子岭流域面雨量), (b) 降水输入为雷达联合6个雨量计反演的各子流域面雨量 (上部为相应的佛子岭流域面雨量) Fig 5. Observed and simulated discharges from 01:00 on June 20 to 00:00 on July 12, 2003 for the Foziling basin (a) from the raingauge-based mean areal rainfall of subcatchments using 6 rain gauges (the upper curve shows the correspongding mean areal rainfall for the Foziling basin), (b) from the adjusted radar-based mean areal rainfall of subcatchments using 6 rain gauges (the upper curve shows the correspongding mean areal rainfall for the Foziling basin) | |
由表 4和图 5可见, 当采用6个雨量计时, 雨量计测值和雷达测值对佛子岭水库入库流量过程的模拟结果相差并不大。
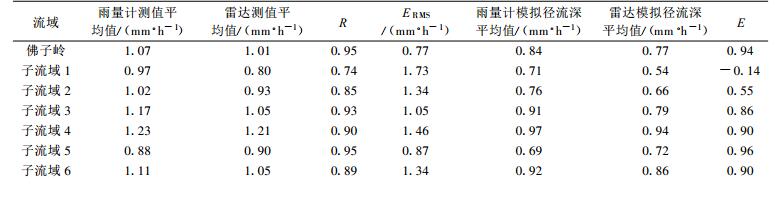
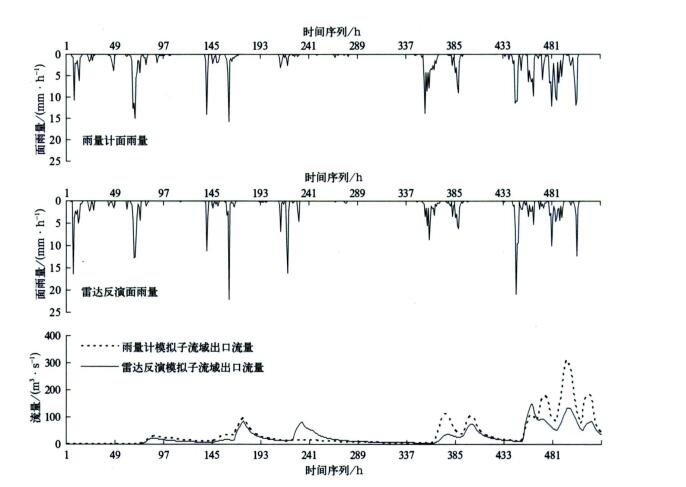
表 5为佛子岭流域及子流域的面雨量和模拟径流深统计, 表中R和ERMS为雨量计测值系列与雷达测值系列的相关系数和均方根误差, E为以雷达模拟径流深为参考流量系列、以雨量计模拟径流深为模拟流量系列时计算的效率系数。表中用到彩图 1c中所示的用于校准的6个地面雨量计。由表 5可知, 当雨量计计算的整个流域面雨量与雷达-雨量计联合校准后的结果接近时, 对应子流域面雨量的结果存在不同程度的差别, 如子流域1的R最小, ERMS最大, 而子流域5的R最大, ERMS最小; 同时, 不同方法计算的某一子流域面雨量的差别越大, 则水文模型输出的该子流域径流深的差别也越大, 如子流域1的E为-0.14, 表明雷达模拟子流域1的径流深与雨量计模拟的径流深差别很大, 这由图 6给出的子流域1的流域面雨量及模拟流域出口流量也可看出, 而子流域5的E为0.96, 不仅在所有子流域中最大, 而且比全流域的大。
|
|
表 5 2003年6月20日至7月12日佛子岭流域及子流域的面雨量和模拟径流深统计 Table 5 Statistics of mean areal rainfall estimates and simulated runoff depths for the Foziling basin with its 6 subcatchments from June 20 to July 12, 2003 |
|
|
| 图 6. 2003年6月20日01:00到7月12日00:00佛子岭流域中子流域1的流域面雨量及模拟流域出口流量 Fig 6. The mean areal rainfall estimates and simulated discharges from 01:00 on June 20 to 00:00 on July 12, 2003 for subcatchmennt 1 of the Foziling basin | |
4 小结
本文以淠河上游的佛子岭闭合流域及用1:250000 DEM数据划分的6个子流域为研究区域, 用地面雨量计和雷达-雨量计联合校准两种方法进行流域面雨量计算, 将两种方法计算的面雨量分别作为TOPMODEL降水-径流模型的输入, 对模型输出结果进行了比较。本文所用资料为“黄淮试验”项目中淮河水利委员会提供的2003年6月20日至7月12日的加密雨量站资料、流域出口流量资料、蒸发资料和气象部门提供的合肥CINRAD/SA雷达体扫原始数据资料。基于以上资料的分析表明:雷达测量降水的精度是否高于单独用地面雨量计计算的精度, 在一定程度上取决于用于校准的地面雨量计的数目和代表性; 当雨量计计算的整个流域面雨量与雷达-雨量计联合校准后的结果接近时, 对应子流域面雨量的结果存在不同程度的差别; 不同方法计算的某一子流域面雨量的差别越大, 则水文模型输出的该子流域径流的差别也越大。
需要指出的是, 文中用到的佛子岭水库入库流量资料没有考虑流域中涵闸等所引起的误差, 同时, 本文得到的结论是基于所选择的TOPMODEL水文模型和雷达联合雨量计的平均校准方法。今后还需要用更多的资料、其他水文模型和更多的雷达联合雨量计校准方法进行深入研究。
致谢 本文在完成过程中, 英国兰喀斯特大学教授Beven K J提供了TOPMODEL模型Windows版本9701和9502版的FORTRAN源程序TMOD9502.for, 在此表示衷心感谢。| [1] | Anagnostou E N, Krajewski W F, Calibration of the WSR-88D precipitation processing subsystem. Wea Forecasting, 1999, 13: 396–406. |
| [2] | Finnerty B D, Smith M B, Seo D J, et al. Space-time scale sensitivity of the Sacramento model to radar-gage precipitation inputs. J Hydrol, 1997, 203: 21–38. DOI:10.1016/S0022-1694(97)00083-8 |
| [3] | 万玉发, 杨洪平, 肖艳娇, 等. 多普勒天气雷达站址视程的客观分析技术. 应用气象学报, 2000, 11, (4): 440–447. |
| [4] | Kucera P A, Krajewski W F, Young C B, Radar beam occultation studies using GIS and DEM technology:An example study of Guam. J Atmos Oceanic Technol, 2004, 21: 995–1006. DOI:10.1175/1520-0426(2004)021<0995:RBOSUG>2.0.CO;2 |
| [5] | Martz W, Garbrecht J, Numerical definition of drainage network and subcatchment areas from digital elevation models. Computers & Geosciences, 1992, 18, (6): 747–761. |
| [6] | Garbrecht J, Campbell J. TOPAZ:An Automated Digital Landscape Analysis Tool for Topographic Evaluation, Drainage Identification, Watershed Segmentation and Subcatchment Parameterization. TOPAZ User Manual, USDA-ARS, Oklahoma, 1997:1-138. |
| [7] | Viessman W, Lewis G L, Introduction to Hydrology. (4th ed). Harper-Collins, 1996: 1-760. |
| [8] | Sun X, Mein R G, Keenan T D, et al. Flood estimation using radar and raingauge data. J Hydrology, 2000, 239: 4–18. DOI:10.1016/S0022-1694(00)00350-4 |
| [9] | 刘晓阳, 毛节泰, 李纪人, 等. 雷达联合雨量计估测降水模拟水库入库流量. 水利学报, 2002, (4): 342–349. |
| [10] | Ren liliang, Li Chunhong, Wang Meirong, Application of radar-measured rain data in hydrological processes modeling during the intensified observation period of HUBEX. Adv Atmos Sci, 2003, 20, (2): 205–211. DOI:10.1007/s00376-003-0005-8 |
| [11] | Liu Xiaoyang, Mao Jietai, Zhu Yuanjing, et al. Runoff simulation using radar and rain gauge data. Adv Atmos Sci, 2003, 20, (2): 213–218. DOI:10.1007/s00376-003-0006-7 |
| [12] | Fulton R A, Breidenbach J P, Seo D, et al. The WSR-88D rainfall algorithm. Wea Forecasting, 1998, 13: 377–395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2 |
| [13] | 尹忠海, 张沛源. 利用卡尔曼滤波校准方法估算区域降水量. 应用气象学报, 2005, 16, (2): 213–219. |
| [14] | 史锐, 程明虎, 崔哲虎, 等. 用反射率因子垂直廓线联合雨量计校准估测夏季区域强降水. 应用气象学报, 2005, 16, (6): 737–745. |
| [15] | 吴翠红, 万玉发, 吴涛, 等. 雷达回波垂直廓线及其生成方法. 应用气象学报, 2006, 17, (2): 232–239. |
| [16] | 曹俊武, 刘黎平, 陈晓辉, 等. 3836C波段双线偏振多普勒雷达及其在一次降水过程中的应用研究. 应用气象学报, 2006, 17, (2): 192–200. |
| [17] | Wilson J W, Brandes E A, Radar measurement of rainfall— a summary. Bull Amer Meteor Soc, 1979, 60: 1048–1058. DOI:10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 |
| [18] | Colle B, Westrick K, Mass C F, Evaluation of MM5 and Eta-10 precipitation forecasts over the Pacific Northwest during the cool season. Wea Forecasting, 1999, 14: 137–154. DOI:10.1175/1520-0434(1999)014<0137:EOMAEP>2.0.CO;2 |
| [19] | Beven K J, Kirkby M J, A Physically based variable contributing area model of basin hydrology. Hydrology Sci Bull, 1979, 24: 43–69. DOI:10.1080/02626667909491834 |
| [20] | Beven K J, Kirkby M J, Schoffield N, et al. Testing a physically-based flood forecasting model (TOPMODEL) for three UK catchments. J Hydrology, 1984, 69: 119–143. DOI:10.1016/0022-1694(84)90159-8 |
| [21] | Beven K J, Lamb R, Quinn P, et al. TOPMODEL ∥VP Singh, Computer Models of Watershed Hydrology, Chapter 18. Water Resources Publications, 1995:627-668. |
| [22] | Saulnier G M, Beven K J, Obled C H, Including spatially variable soil depths in TOPMODEL. J Hydrology, 1998, 202: 158–172. |
| [23] | 郭方, 刘新仁, 任立良. 以地形为基础的流域水文模型———Topmodel及其拓宽应用. 水科学进展, 2000, 11, (3): 296–301. |
| [24] | 熊立华, 郭生练, 胡彩虹. TOPMODEL在流域径流模拟中的应用研究. 水文, 2002, 22, (5): 5–8. |
| [25] | 陈仁升, 康尔泗, 杨建平, 等. TOPMODEL模型在黑河干流出山径流模拟中的应用. 中国沙漠, 2003, 23, (4): 428–433. |
| [26] | Nash J E, Sutcliffe J V, River flow forecasting through conceptual models, Ⅰ:A discussion of principles. J Hydrol, 1970, 10: 282–290. DOI:10.1016/0022-1694(70)90255-6 |
 2007, 18 (3): 295-305
2007, 18 (3): 295-305