应用气象学报  2007, 18 (3): 276-284   PDF    
引用本文
胡江林, 沈学顺, 张红亮, 杨学胜, 王盘兴. GRAPES模式动力框架的长期积分特征[J]. 应用气象学报, 2007, 18(3): 276-284.
Hu Jianglin, Shen Xueshun, Zhang Hongliang, Yang Xuesheng, Wang Panxing. Characteristics of GRAPES Dynamical Core in Long Term Integration[J]. Journal of Applied Meteorological Science, 2007, 18(3): 276-284  
GRAPES模式动力框架的长期积分特征
胡江林1,2, 沈学顺2, 张红亮2, 杨学胜2, 王盘兴1     
1. 南京信息工程大学大气科学系, 南京 210044;
2. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
2006-03-08 收到, 2007-01-12 收到修改稿.
资助项目: 国家“十五”科技攻关课题 (2004BA607B01) 和国家自然科学基金项目 (40675062, 40505023) 共同资助    
摘要: 通过考虑动量表面拖曳并利用牛顿松弛方法将温度松弛到纬向对称的温度场, 对GRAPES模式的动力框架进行了长期时间积分试验。通过统计分析其积分结果表明:GRAPES模式的动力框架可以模拟出大气环流的基本特征; 随着分辨率的提高, GRAPES模式动力框架的模拟结果显示出收敛的特性; 虽然GRAPES模式动力框架采用的是能量不守衡的半隐式半拉格朗日时间积分方案, 但长期时间积分试验表明其能量基本保持稳定。这些结果显示使用GRAPES模式动力框架作大气环流和气候研究的大气动力框架是可行的, 同时也为进一步改进GRAPES模式动力框架提供了线索和依据。
关键词: 基准测试    大气环流模式    动力框架    数值试验    
Characteristics of GRAPES Dynamical Core in Long Term Integration
Hu Jianglin1,2, Shen Xueshun2, Zhang Hongliang2, Yang Xuesheng2, Wang Panxing1     
1. Department of Atmospheric Sciences, Nanjing University of Information & Technology, Nanjing 210044;
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
Abstract: In order to evaluate the characteristics of the dynamical core of GRAPES (Global/Regional Assimilation and PrEdiction System) and to verify whether the GRAPES dynamical core can be taken as a framework of AGCM, the long time integration has been carried out with GRAPES dynamical core followed by the benchmark test similar to the technique introduced by Held and Suarez. The GRAPES has a finite-difference dynamical core with fully compressible, non-hydrostatic framework and semi-implicit and semi-lagrangian (SISL) time integration scheme using latitude and longitude horizontal coordinate as well as following terrain height vertical coordinate. The computational design uses two simple physical processes to represent physics processes in the model during the time integration. The first process is to relax the model variant, potential temperature, to a prescribed potential temperature field which is a function of latitude and height during the model time integration. Following Held and Suarez, the second one is the momentum drag in the lower troposphere to consume the kinetic energy in the model atmosphere. The GRAPES dynamical core runs with 31 levels in vertical direction and 3 horizontal resolutions:1.25°, 2.5°and 5.0°latitude or longitude. The benchmark tests integrate for 1460 days under each horizontal resolution and the last 1000 days data are analyzed by discarding the previous 460 day results. The statistic results show that the GRAPES dynamical core can reproduce basic features of atmospheric circulation, including reasonably realistic zonal mean temperature and its eddy variance as well as zonal-mean wind and its eddy variance. A single westerly jet is generated with maximum strength of roughly 28 m/s near 45°latitude in the tropopause. And eddy temperature variance shows two middle latitude maxima, one in the low troposphere and the other above tropopause. The GRAPES dynamical core also shows stability for the energy and momentum as well as vertical wind speed during the long term integration although SISL scheme does not observe the conservations. The GRAPES dynamical core has convergence features along with increasing resolution, although 5.0° resolution in latitude and longitude may be too coarse to represent the circulation details. Finally, the sensitivity to non-hydrostatic is discussed. The results indicate that it is feasible using the GRAPES frame as a dynamical core for AGCM and climate investigation. The numerical experiments provide clues and evidences for GRAPES dynamical core improvement also.
Key words: benchmark tests     AGCM     dynamical core     numerical experiments    
引言

GRAPES系统[1-5]是在中国气象局与国家科技部共同支持下, 由中国气象局、中国科学院大气物理研究所、北京大学、南京大学、南京信息工程大学等多部门科学家协同努力在“十五”期间研发的新一代非静力数值天气预报系统, 现已使用GRAPES动力框架在国家气象中心建立了有限区域和全球预报试验系统[6], 在上海台风研究所建立了台风预报试验系统, 在广州热带海洋气象研究所建立了中尺度预报试验系统, 在兰州干旱气象研究所建立了西北地区沙尘暴数值预报模式[7]。将该数值天气预报模式的动力框架进一步用于大气环流和短期气候的数值研究是GRAPES模式一个自然而然的发展[8]。将GRAPES模式用于大气环流和短期气候研究之前, 了解GRAPES模式的长期积分性能至关重要。

国内外对大气环流模式的动力框架性能都十分重视, 例如Arakawa最早提出动能和涡度拟能的守恒问题[9], Zhang等对中国科学院大气物理研究所的IAP AGCM-Ⅰ模式的动力框架进行了比较和检验[10], 左瑞亭等利用Rossby-Haurwitz波的波型、能量、波速对IAP AGCM-Ⅲ模式的动力框架进行了检验[11], 而梁丹青等[12]和王斌等[13-14]则分别利用NCEP/NCAR再分析资料对各自发展的分块地形坐标大气环流模式和等面积网格的大气环流模式进行了模拟对比检验, 这些工作对检验模式的性能和稳定性有重要意义。

大气环流模式长期积分效果受到许多因素影响。例如云和辐射等物理过程对模式大气的非绝热加热有决定性影响, 海表和地表温度等边界条件对模式的积分效果也有很大作用, 而模式的动力框架在气候和大气环流模式中处于核心地位, 其长时间积分特征对认识模式性能有特别重要的意义。但由于模式中物理过程和大气动力学过程间相互作用的复杂性, 通过对比完全物理过程的大气环流模式的长期时间积分和实际观测两者之间的差异, 有时仍不能确定模式误差的来源和模式的改进方向, 解决这一问题的方法是将大气环流模式的物理过程和大气动力框架分别进行独立测试和比较。自Gates提出进行大气模式比较计划[15]以来, 检验模式动力框架性能的工作逐渐受到关注, Williamson等则提出用二维的球面浅水波方程的检验来替代对三维的AGCM的检验, 并提出了一组测试集试验来检验球面浅水波方程[16]。Held等利用牛顿松弛和表面拖曳两个简单物理过程的指定, 来检验大气环流模式的时间平均场[17]。而Boer等则讨论了大气环流模式数值解随分辨率的收敛性[18], Polvani等则提出了测试大气环流模式涡度和垂直速度随时间演变的方法[19]。这些研究可归纳为设定一组标准试验, 包括理想的初始场和统一的边界条件, 通过分析长时间积分试验的结果来检验模式动力框架的性能, 为模式的大气环流和气候研究提供基础支持, 已成为大气环流新模式发展的必需工作[20]。

本文仿Held和Suarez提出的利用牛顿松弛和表面拖曳这两个简单物理过程的指定, 来检验GRAPES模式动力框架的长时间积分性能。

1 模式及试验方案简介 1.1 GRAPES模式简介

GRAPES模式是一个格点模式, 它的动力框架使用一套含完全动力学过程的非静力、全可压的方程组, 并使用静力平衡的参考廓线, 积分方案使用两时间层的半隐式半拉格朗日时间差分方案, 空间差分水平方向上采用Arakawa C跳点格式, 垂直方向采用Charney-Philips跳点格式, 拉格朗日插值采用三维的准三次多项式。采用了矢量场离散化技术来计算曲率项和解决两极地区的矢量计算问题。使用广义共扼余差 (GCR) 方法求解关于扰动气压的三维Helmholtz方程。由于采用的半隐式半拉格朗日积分方案本身有一定的稳定性, 除80°以外的极冠地区使用了显式方案的滤波外, GRAPES模式没有显式的扩散方案。

不含水物质和物理过程的GRAPES模式动力框架方程组[3]是:

(1)
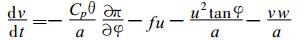
(2)
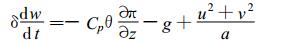
(3)
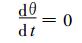
(4)
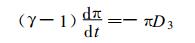
(5)

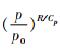
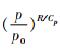
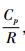
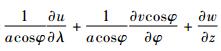
式 (1)~(5) 中, 位温θ=T, p0是参考气压, GRAPES模式取1000 hPa, ε=0.608, g=9.81 m/s2, 气压变量π=, a=6.371 ×106 m为地球半径, λ为经度, φ为纬度, δ是非静力 (δ=1)/静力 (δ=0) 选项开关, γ=, Cp=1004 J·kg-1·K-1, R=287 J· kg-1·K-1, 地球自转角速度Ω=7.292 ×10-5s-1, 三维散度D3=, 其他为气象上的常用符号。

GRAPES模式水平方向上采用经纬度的球面坐标, 垂直方向采用地形高度追随坐标:

(6)

式 (6) 中, Zs是地形高度, ZT是模式层顶的位势高度。

1.2 试验方案

参照文献[17], 给定动量表面拖曳和利用牛顿松弛法将温度松弛到纬向对称的温度场, 通过理想场试验的方法来检验GRAPES模式动力框架的长期时间积分特征。温度场的松弛使得模式大气的温度在积分过程中不至于过度偏离实际大气, 而表面拖曳的指定实际上给模式加上了动能耗散, 其消耗的动能将通过牛顿松弛得到的位能进行补偿。该方案现已成为大气环流模式的基准测试方法。为此, 在位温预报方程中加入牛顿松弛项, 式 (4) 变为:

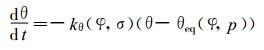
(7)

式 (7) 中, kθ是松弛系数, 它是一个纬度和高度的函数, 该值越大表明松弛作用越强。

(8)

式 (8) 中, ka=1/40 d-1, ks=1/4 d-1, σ=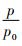, p为静力学压力, p0=1000 hPa, σb=0.7。而θeq为纬向对称的平衡位温, 它应为模式大气应该趋向的平均位温, 假定为:

(9)

式 (9) 中, κ=, Δθy=60 K, Δθz=10 K。通过Δθy和Δθz两个简单的参数, 式 (9) 指定了平衡位温θeq随纬度和高度的分布。从图 1可见, θeq与实际大气的位温分布很相近, 它关于南北半球是对称的。

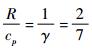
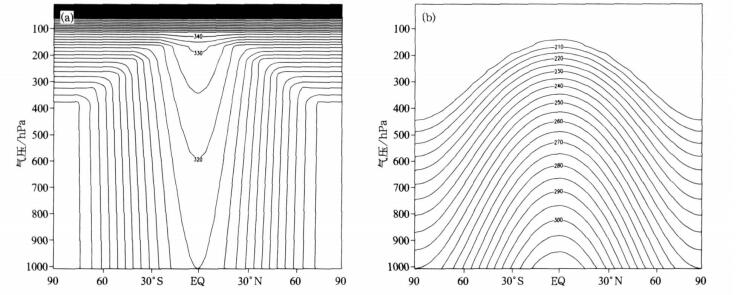
图 1. 平衡位温θeq (a) 和温度 (b) 随纬度和高度的分布 (单位:K) Fig 1. The distributions of equilibrium potential temperature (a) and temperature (b) with latitude and air pressure (unit:K)

在水平动量方程中加入表面拖曳项, 式 (1) 和式 (2) 变为:

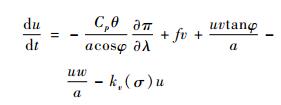
(10)
(11)

其中

(12)

这里kf=1 d-1。引入该项的物理意义是实际大气中对流层低层是摩擦耗散层, 它强烈地消耗着大气的动能。如果不在模式中引入该过程, 所有模式模拟的风场将过强。

为了和文献[17]的结果进行对比, 本文上述两物理过程中的所有参数与文献[17]均完全一致。但由于GRAPES模式预报变量是位温, 所以已将文献[17]的温度松弛指定转为位温松弛, 另外, 与文献[17]不同的是GRAPES模式采用的是地形高度追随坐标, 本文也已将文献[17]中的气压函数处理成相应的高度函数。

本文的试验中, 垂直方向取31层, 静力开关选项δ=1, 不考虑地形的影响, 时间步长取20 min, 积分4个模式年共1460 d, 以下所有的分析都取自模式时间积分的后1000 d逐日的模拟结果。模式初始场资料取自2004年1月1日20:00(北京时, 下同) 国家气象中心的T213模式分析场, GRAPES模式初值的形成方案参见文献[5]。实际上由于本文研究的是GRAPES模式时间积分的长期特征, 积分结果的前460 d资料不进行分析, 可认为积分结果与模式初值无关, 因而可取任一天的T213资料作试验初值。

虽然GRAPES模式的水平分辨率是可调的, 但由于计算量的限制, 只进行了5°×5°, 2.5°×2.5°和1.25°×1.25°共3种水平分辨率的试验。除第3章中分析模式的收敛外, 本文只分析最高分辨率1.25°×1.25°的结果。需要说明的是, 对于气候模式1.25°×1.25°的水平分辨率和31层的垂直分辨率是现有条件下能达到的较高分辨率。

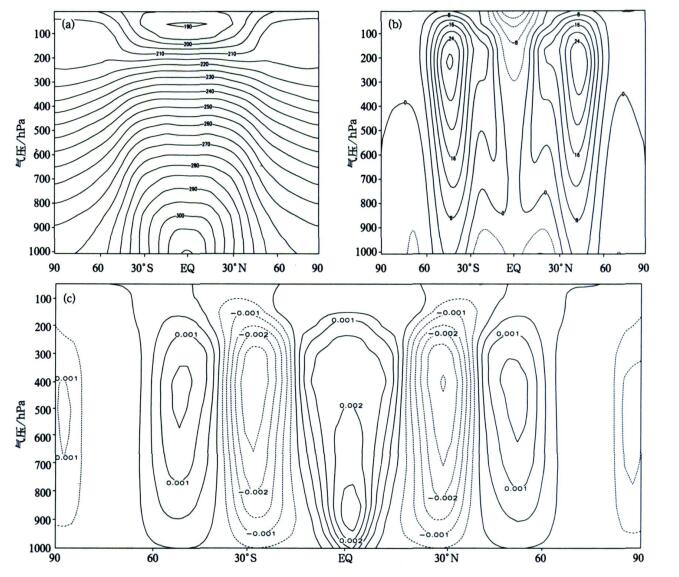
2 积分结果的统计检验

由于给出的强迫关于南北半球完全对称, 因而理论上积分结果在南北半球也应该是对称的, 而其间的非对称被认为是统计抽样不同而引起。图 2显示无论是温度 (图 2a) 还是纬向风速 (图 2b) GRAPES模式的积分结果在南北半球基本对称, 后面分析的其他结果也可以看到GRAPES动力框架的其他计算结果在南北半球是基本对称的。

图 2. 1.25°×1.25°31层GRAPES动力框架长时间 (1000 d, 下同) 积分的纬向平均温度 (单位:K)(a), 纬向风速 (单位:m/s)(b) 和纬向平均的垂直速度 (单位:m/s)(c) Fig 2. The averaged fields with 1000 d simulations produced by GRAPES dynamical core using the resolution of 1.25°×1.25°grid points and 31 levels (a) zonal mean temperature (unit:K), (b) mean zonal wind (unit:m/s), (c) zonal vertical speed (unit:m/s)

由图 2可知, 通过牛顿松弛项的方式, 用式 (9) 给定纬向对称的温度场强迫和用式 (12) 给定表面拖曳这两个简单物理过程, 仅用Δθy, Δθz和kf几个参数, GRAPES模式动力框架就可模拟出大气平均状态的主要特征, 包括低纬地区平流层的低温和中纬度对流层的锋区, 低纬和两极地区的东风带和中纬地区的西风带, 特别是对流层顶附近的西风急流。这些系统的位置和强度与实际大气相一致, 例如低纬地区平流层的最低温度为190 K左右, 中纬度对流层顶平均风速为25 m/s, 这与文献[17]的基准测试结果相吻合, 也与实际大气的平均状况基本相符。这反映出GRAPES动力框架能较好地模拟大气的大尺度过程, 进而模拟出大气环流的平均状态。

与静力模式不同的是, GRAPES模式的垂直速度是独立的预报变量, 纬向平均的垂直速度剖面 (图 3c) 显示赤道地区是上升区, 30°左右的副热带地区是下沉区, 而40°到60°中纬度地区是上升区, 极区又是下沉区。除赤道地区外, 各极值中心数值为0.003 m/s左右, 都在500 hPa左右, 从分布型和极值数量上与文献[14]中多年平均的垂直速度基本一致, 也可以进一步推测GRAPES模式对经圈上的3个环流圈的模拟是基本正确的。

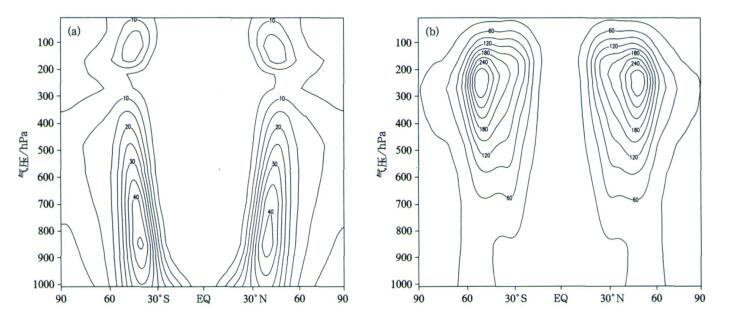
图 3. 1.25°×1.25°31层GRAPES动力框架长时间积分 (a) 纬向平均温度方差 (单位:K2), (b) 纬向风速方差 (单位:m2·s-2) Fig 3. The eddy variance with 1000 d simulations produced by GRAPES dynamical core using the resolution of 1.25°×1.25°grid points and 31 levels (a) temperature (unit:K2), (b) zonal wind (unit:m2·s-2)

图 3是GRAPES模式温度和纬向风速的方差的计算结果。在中纬度40°左右对流层低层850 hPa和对流层顶150 hPa左右各有一极值中心, 且中心强度与文献[17]的基准测试结果一致 (图 3a)。而纬向风速在50°左右的对流层高层250 hPa有方差的极大值 (图 3b), 这些特点都基本反映了实际大气环流的特点。特别需要指出的是, 图 3a显示GRAPES模式在赤道地区的对流层低层的温度方差非常小, 这与实际大气的状况一致, 克服了文献[17]中模拟的低纬度地区温度方差比实际大气偏大的缺点。这表明GRAPES模式模拟的热带中低层受中纬度波动的影响与实际较接近, 而文献[17]所列的模式模拟的热带大气受中纬度的冷空气影响过强。造成这种现象的原因尚不清楚, 可能的解释是GRAPES模式平流采用拉格朗日算法, 而文献[17]所列的模式均采用欧拉算法, 拉格朗日算法能更好地描述东西风切变在中纬度西风带的冷空气活动向热带传播过程中所起的阻止作用。另一可能原因是GRAPES模式是非静力模式, 对热带地区的对流活动的模拟效果或许比静力模式强, 导致GRAPES模式在热带地区的模拟效果较好。

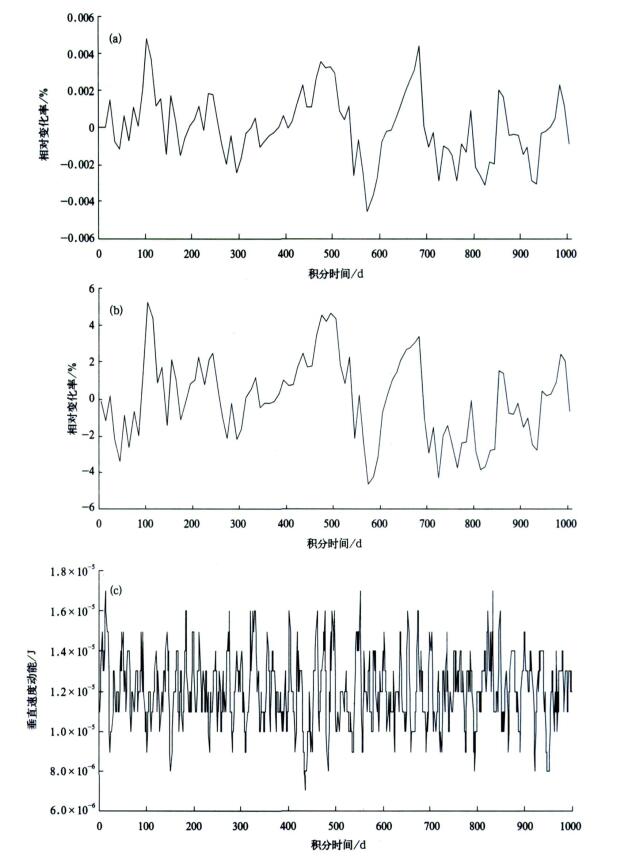
3 模式的稳定性分析与收敛性

模式的稳定性检验是模式研发过程中十分重要的一环。图 4a~4c是GRAPES模式动力框架的总能量、纬向风动量和垂直速度随模式积分时间的变化情况。定义全球大气内能、位能和动能的体积分之和为总能量Esum, 即

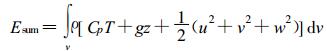
(13)

式 (13) 中变量符号为气象上通用的。图 4a表明模式积分过程中总能量Esum是守衡的, 它在总共1000 d的时间积分过程中, 其最大变幅不超过万分之一, 并且没有明显的增加或减少的趋势。

图 4. 1.25°×1.25°31层GRAPES模式动力框架长时间积分的物理量随时间变化 (a) 总能量, (b) 纬向风动量, (c) 单位质量的垂直速度动能 (全球平均) Fig 4. The variables produced by the 1.25°×1.25°grid points and 31 levels GRAPES dynamical core with 1000 d simulation (a) general energy, (b) the zonal wind moment, (c) kinetic energy produced by vertical movement per unit mass (averaged by global)

图 4b表明模式长时间积分过程中纬向风 (西风) 动量基本守衡, 但其变化幅度较大, 最大变幅可以达到10%, 可以认为模式内存在明显的纬向风动量振荡, 但也没有明显的增加或减少的趋势。图 4c是全球平均的单位质量大气所具有的垂直速度动能, 图中显示在1000个积分日中单位质量大气的垂直速度动能存在一定的振荡, 变化在0.8~1.7 J之间, 但垂直速度动能的平均值不存在明显的增加或减小的趋势。

模式的分辨率对长期积分结果的影响也是大气环流模式研究者十分关心的问题之一。模式计算结果是否收敛, 即随着模式分辨率的增加, 模式的计算结果是否趋于一致?以及在什么分辨率情况下模式的计算结果可能收敛。

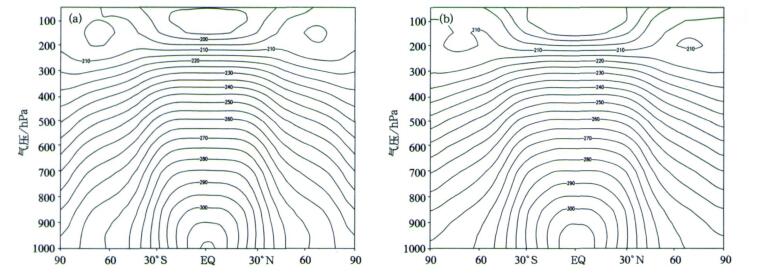
分析图 5和图 2a可以发现, 对纬向温度场而言, 虽然5°×5°的模式分辨率模拟出的中纬度大气环流的平均情况与其他两种分辨率的结果比较相近, 但赤道地区的高层没有模拟出闭合的冷涡, 高层最低仅为194 K, 而地面的温度也模拟过低。但2.5°×2.5°分辨率的高层最低为191 K, 与1.25°×1.25°分辨率的189 K更相近, 后两者的模拟结果不仅在中高纬地区基本相近, 在赤道地区也比较类似, 两者在高层有闭合的冷涡, 而地面的温度都超过了310 K。

图 5. 不同水平分辨率的GRAPES动力框架长时间积分纬向平均温度场 (单位:K)(a)2.5°×2.5°, (b)5.0°×5.0° Fig 5. The zonal mean temperature averaged with 1000 d simulations produced by GRAPES dynamical core with varied horizontal resolutions (unit:K)(a)2.5°×2.5°, (b)5.0°×5.0°

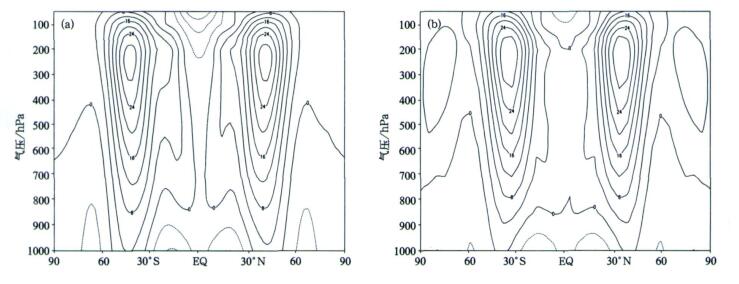
进一步分析纬向平均风速的情况 (图 6和图 2b) 也可以发现, 虽然各种分辨率对西风急流的模拟比较相近, 为28~30 m/s, 但5°×5°分辨率的模式在低纬赤道地区和两极地区的模拟结果与其他两种分辨率比较有一定差距。主要是赤道地区模拟的高层东风强度过于偏弱, 东风极值不到5 m/s, 而两极地区高层又有偏强的西风, 而2.5°×2.5°和1.25°× 1.25°分辨率两者的结果比较一致, 赤道高层的东风极值都超过了12 m/s。

图 6. 不同水平分辨率的GRAPES动力框架长时间积分纬向平均风速 (单位:m·s-1)(a)2.5°×2.5°, (b)5.0°×5.0° Fig 6. Same as in Fig. 5 but for zonal wind (unit:m·s-1)(a)2.5°×2.5°, (b)5.0°×5.0°

从以上分析可知, 当GRAPES模式的水平分辨率达2.5°×2.5°以上时可以得到平均纬向环流基本一致的温压场和流场, 在这个意义上可以说在该分辨率下GRAPES模式的模拟结果开始收敛。这与文献[18]指出的谱模式开始收敛的分辨率大致相同。

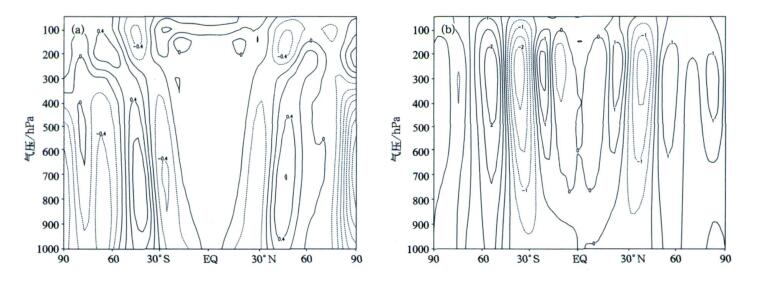
最后再分析一下非静力过程在GRAPES模式长期数值积分中的作用。将式 (3) 中的δ参数取0即可得到静力情况的结果。分析非静力减静力的纬向平均的温度和纬向风随高度变化 (图 7a), 可以发现在分辨率为1.25°×1.25°的情况下非静力的作用相对较小。两种情况下纬向平均的温度差不超过0.5 K, 在非静力的条件下, 中低纬度间对流层中下层的温度梯度比静力情况下略有增大; 而纬向风速差基本不超过2 m/s (图 7b), 在对流层风速极区西风略有增强, 中纬度西风略有减小, 但这种变化总的说来并不特别明显, 即在1.25°×1.25°分辨率条件下GRAPES模式模拟的还主要是大尺度系统, 非静力效应并不十分显著, 这与实际大气也是基本一致的。

图 7. GRAPES动力框架长时间积分的纬向平均温度 (单位:K)(a) 和纬向平均风速 (单位:m/s)(b) 的对比 (非静力-静力) Fig 7. The difference between nonhydrostatic and hydrostatic for zonal mean temperature (unit:K)(a) and wind (unit:m/s)(b) with 1000 d simulations produced by GRAPES dynamical core

4 结论与讨论

在大气环流模式的研发和评估模式性能的工作中, 全面测试和仔细评估其动力框架长期时间积分效果是必不可少的步骤, 也是国内外气象科技界的通常做法。本文应用牛顿松弛法, 将温度松弛到纬向对称的温度场并给定动量表面拖曳, 在设定31层、1.25°×1.25°较高分辨率的情况下对GRAPES模式的动力框架进行了长达4年的时间积分试验, 并对其中后1000 d的计算结果进行了分析和检验, 可得到以下结论:

1) GRAPES模式的动力框架可以模拟出大气环流的基本特征, 模拟的温度场和纬向风场的纬向平均值和方差与基准测试的结果非常相近, 特别是在赤道地区的对流层低层的温度方差非常小, 克服了基准测试中模拟的低纬度地区温度方差比实际大气偏大的缺点。

2) 虽然GRAPES动力框架采用半隐式半拉格朗日时间积分方案, 但在长时间积分过程中可以保证能量守衡和动量守衡。

3) 随着分辨率的提高, GRAPES模式动力框架的模拟结果显示出收敛的特性。

以上研究结果是初步的, 但这些结果表明使用GRAPES模式动力框架作大气环流和气候研究的大气动力框架是基本可行的, 同时也将为进一步改进GRAPES模式动力框架提供了线索和依据。

参考文献
[1] 陈德辉, 薛纪善. 数值天气预报业务模式现状与展望. 气象学报, 2004, 62, (5): 623–633.
[2] 薛纪善. 新世纪初我国数值天气预报的科技创新研究. 应用气象学报, 2006, 17, (5): 601–610.
[3] 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777.
[4] 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16, (4): 539–546.
[5] 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16, (3): 374–384.
[6] 叶成志, 欧阳里程, 李象玉, 等. GRAPES中尺度模式对2005年长江流域重大灾害性降水天气过程预报性能的检验分析. 热带气象学报, 2006, 16, (4): 539–546.
[7] 李耀辉, 赵建化, 薛纪善, 等. 基于GRAPES的西北地区沙尘暴数值预报模式极其应用研究. 地球科学进展, 2005, 20, (9): 999–1011.
[8] 章建成, 刘奇俊. GRAPES模式不同云物理方案对短期气候模拟的影响. 气象, 2006, 32, (7): 3–12.
[9] Arakawa A, Computational design for long-term numerical integration of the equations of fluid motion:Two-dimensional incompressible flow, part Ⅰ. J Comput Phys, 1966, 1: 119–143. DOI:10.1016/0021-9991(66)90015-5
[10] Zhang Xuehong, Liang Xinzhong, Comparison and examination of dynamic frameworks of IAP and OSU AGCM. Adv Atmos Sci, 1989, 6: 265–274. DOI:10.1007/BF02661533
[11] 左瑞亭, 张铭, 张东凌, 等. 21层大气环流模式IAP AGCM-Ⅲ的设计及气候数值模拟:Ⅰ动力框架. 大气科学, 2004, 28, (5): 659–674.
[12] 梁丹青, 张铭, 曾庆存. 分块地形坐标大气环流模式框架的计算稳定性及数值试验. 大气科学, 2005, 29, (3): 354–362.
[13] Wang Bin, Wan Hui, Ji Zhongzhen, et al. Design of a new dynamical core for global atmospheric models based on some efficient numerical methods. Science in China Ser A Mathematics, 2004, 47: 4–21. DOI:10.1360/04za0001
[14] 王斌, 季仲贞. 大气科学中的数值新方法及其应用. 北京: 科学出版社, 2006: 200-205.
[15] Gates W L, The atmospheric model intercomparison project. Bull Amer Meteor Soc, 1992, 73: 1962–1970. DOI:10.1175/1520-0477(1992)073<1962:ATAMIP>2.0.CO;2
[16] Williamson D L, Drake J B, Hack J J, et al. A standard test for numerical approximations to the shallow water equations in spherical geometry. J Comput Phys, 1992, 102: 211–224. DOI:10.1016/S0021-9991(05)80016-6
[17] Held I H, Suarez M J, A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models. Bull Amer Meteror Soc, 1994, 75: 1825–1830. DOI:10.1175/1520-0477(1994)075<1825:APFTIO>2.0.CO;2
[18] Boer G J, Denis B, Numerical convergence of the dynamics of a GCM. Climate Dyn, 1997, 13: 359–374. DOI:10.1007/s003820050171
[19] Polvani L M, Scott R K, Thomas S J, Numerical converged solutions of the global primitive equations for testing the dynamical core of atmospheric GCMs. Mon Wea Rev, 2004, 132: 2539–2552. DOI:10.1175/MWR2788.1
[20] Trenberth K E, Olson J G. ECMWF Global Analyses 1979-1986: Circulation Statistics and Data Evalution. NCAR/TN-300+STR, NCAR Technical Note, 1988.