小型农田防护林是保护农作物使之所受风沙等气象灾害得以减轻的一种防风设施, 是一种风障。气象条件对风障 (农田防护林) 乃至对其保护下的农作物的增产作用历来为森林气象研究者所重视, 多年来在这方面研究取得了一系列重要成果[1-3]。关于农田防护林对农作物产量的影响, 贺庆棠[4]作过详细评述。以往农田防护林带设计[1-3], 一般主要考虑当地气候条件, 尤其是风向和风力。但由于气候条件是指多年平均状况, 不能说明风的年际变化特征, 只有同时考虑到风的年际变化、天气与风障配合的变化和被保护的农作物, 并将三者作为一个系统来研究, 才更具有合理性。为此, 本文试图在前人大量工作的基础上, 从“天气-风障-产量”这一复杂动态系统出发, 用马尔可夫过程原理[5-9]和运筹学中的一种新的决策技术———马氏决策过程 (Markov decision process, MDP) 对护田林带结构进行抉择, 采用透风结构, 还是疏透结构?
1 材料和方法本研究以沈阳市康平县海洲乡农田防护林为研究对象, 并以内蒙古科左后旗浩坦苏木作为对照, 进行观测和调查。为取得透风结构和疏透结构的林带防风效应数据, 对林带防风效应进行观测, 同时调查在不同结构防护林带保护下的玉米作物增产效果。该项研究中风力和温、湿度对比观测 (分别用转杯风速表和阿斯曼通风干湿表) 于1992—1993年按文献[4]中的方法进行。调查工作自1992年春季开始, 一直持续到2004年秋季。被调查的地块共30块, 每块为0.21 hm2。这些地块有15块在通风林带保护下, 另有15块在疏透林带保护下。每年调查气象产量实况和天气实况 (分为风沙不太严重年份和风沙严重年份两类), 并据调查资料, 计算有关转移概率。这里所说的概率指相应的频率。由于调查的对象为30×13=390个, 样本容量较大并且是随机的, 故用频率代表概率是比较合理的。
农田防护林带的设计和建设是关系到气象条件的生态控制实践的一项具体行动措施。反过来, 这一措施可视为生态动力学[10-12]和生态控制原理[11-12]的一种应用。路甬祥[13]指出: “生态控制原理主要研究生态系统的结构、过程及其人为调控, 使其朝着有利于人类生存与发展的方向演变。该原理可用于农业、林业、牧业、湿地等产业调整和生态环境建设。”
从客观实际情况来看, 像沈阳市康平县海州乡那样的气候环境恶劣、风沙灾害严重的地区, 尽管几十年来农田防护林建设和改造成绩卓著, 在抗御风沙保护大田作物方面取得良好的生态经济效益, 但是随着时间的推移, 原有林带多有破损, 重新建设林带势在必行。既要重新造林, 就必须重新设计, 这实质上是一个涉及生态控制原理的设计过程。
国内外许多学者对农田防护林改造和设计方案做过许多研究[3, 14-15]。这些研究大都是从林带结构与风的动力关系出发的理论研究或风洞模拟, 所用数学方法大都属于确定性方法, 对农田防护林理论做出了重要贡献。在诸如防护林走向决策, 按当地主风向 (比如海洲乡的主风向为NNW) 设计的许多问题中, 确定性数学模型的运用是合理的, 但是在“天气-风障-产量”系统中, 涉及到生态、经济和可持续发展的诸多复杂问题在目前尚不能用微分方程表示, 以致不得不采用随机数学方法尤其要用有关的系统工程方法作优化设计。林带结构类型的选择涉及到复杂的巨系统, 全面论证和表述该系统须用钱学森等倡导的综合集成方法论[16-17], 在现阶段客观条件远不具备。为解决林带结构优化设计问题, 在现有的条件下, 只能抓住其中的一项主要矛盾, 即防护林对产量的影响作为切入点进行初步研究。考虑到海洲乡农田防护林带的实际情况, 本文只研究林带结构抉择这一关键问题。从通风结构 (透风系数为0.55) 和疏透结构 (透风系数为0.35) 这两种林带中选出一种。在农田防护林建设和具体设计中, 如果在某一地区, 疏透结构林带保护农田增产增收的经济效果超过通风结构林带, 尽管为建设这样的林带所需投入多, 也应当采用; 而如果两种结构 (通风结构和疏透结构) 林带保护农田之效果相近, 则宜采用通风结构, 否则造林投入资金会增加。本文拟试用现代运筹学中的马氏决策过程中的折扣模型, 在实际调查资料的基础上, 探讨农田防护林设计中林带结构类型的抉择方法问题。
为满足本研究需要, 引用气象增产值和状态的概念。气象增产值是在气象产量基础上计算出来的, 多年来“气象产量”概念在我国农业气象界被广泛应用。王馥棠等[18]对此概念及产量模拟问题作过全面论述, 近年来也有许多研究者运用了产量模拟与分析方法[19-22]。本文将讨论的气象增产值系指由于农田防护林的气象防护作用而使被保护农田中种植作物增产而形成的产值。在防护林的作用下, 气象增产值应该有多种情况, 但如果按实际数字分得太细, 则无法使用MDP模型。为此, 根据事件概率估计原则, 在此取两分类值, 即两种状态:气象增产作用明显, 林带结构与自然气象条件配合得好, 即风沙不太严重 (当地玉米生育期内平均大风日数为20 d, 小于20 d为“不太严重”) 年份, 配合通风结构林带, 或风沙严重 (大风日数等于或大于20 d为“严重”) 年份, 配合疏透结构林带, 记为状态1;气象增产作用不明显, 林带结构与自然气象条件配合得不好, 即风沙不太严重年份, 配合疏透结构林带, 或风沙严重年份, 配合通风结构林带, 记为状态2。
“天气-风障-产量”系统涉及大气环流系统、天气形势、风障 (防护林) 结构、农作物生物学特性、土壤经营管理、农产品价格等多种因素, 可认为是一个复杂巨系统[16]。在该系统中, 作物产量、产值受多种因素制约, 确切地分离出某一种因素的作用在现阶段是不可能的。处理这类复杂巨系统的最好办法是用钱学森等[16]提出的综合集成方法论。本文参考前人的有关论述、计算方法、实验资料、生产者和管理者的经验, 求算气象增产值。贺庆棠[4]给出林网内农作物平均增产5%~15%的估算结果。为大概分辨出防护林通过防御气象效应生态逆境而显示出来的防护效益乃至增产增收效果。本文借用农业气象中常用的气象产量估算原理, 举出计算的一个例子。因为作物实际产量的形成涉及自然条件和社会等诸多因素, 而气象因素 (温度、日照、湿度、风等多种气象要素的作用综合为气象因素) 只是自然因素的一种, 气象产量是实际产量减去趋势产量所得的差值, 对于防护林气象增产作用, 这个定义也是适用的。计算以状态1情形下26.7 hm2面积为研究对象, 计算气象增产值的步骤如下: ①据当地多年玉米产量统计数据, 用文献[23-24]方法绘出趋势产量曲线; ②根据实验地产量资料, 以实际产量减去趋势产量, 得气象增产量为580.5 kg/hm2; 按20世纪80年代末售价0.40元/kg计, 算出气象产值为: 232.2元/hm2, 并有232.2元/hm2×26.7 hm2≈6200元, 此即状态1情形下总气象增产值。同样, 可计算出状态2情形下总气象增产值为-3100元。
由此可知, 如果气象增产作用明显, 一年可获利6200元 (按气象增产值计, 下同); 如果气象增产作用不明显, 一年可获利-3100元。在上述两种状态的每一种状态下, 可用的行动均有两种:采用通风结构, 记作b; 采用疏透结构, 记作c; 假定在采用通风结构林带 (即采用行动b) 时, 不须增加资金投入, 防护林正常维护的追加费用被假定为零; 而采用疏透结构林带 (即采用行动c) 时, 一年要追加投入被估算为2100元的费用。
据调查可知:系统处于状态1, 采用行动c, 由于各种随机因素的干扰, 下一年仍处于状态1的概率为0.81, 而转为状态2的概率为0.19;系统处于状态1, 采用行动b, 下一年仍处于状态1的概率为0.52, 而转为状态2的概率为0.48;系统处于状态2, 采用行动b, 下一年转为状态1的概率为0.41, 仍处于状态2的概率为0.59;系统处于状态2, 采用行动c, 下一年转为状态1的概率为0.72, 仍处于状态2的概率为0.28。
依据MDP有关基本原理[6-9], 用群决策中的Delphi法[25], 对有经验的28位专家进行三轮调查, 最终结果表明:折扣因子平均值被估计为0.904, 均方差为0.018。这是考虑到“天气-风障-产量”系统长期折扣效益, 按“人民币汇率基本稳定”这一事实估计出的折扣因子, 故在本研究中取β=0.9。
2 结果分析本研究所涉及的是随机性问题, 而且由防护林玉米作物、天气、人为调控诸多因素构成的系统, 在某一年所处的状态与其相近年份 (前一年) 有一定关系, 但与其前2~5年的状态关系甚微, 在本研究的精度下, 可认为是无后效的随机过程, 即数学中所说的马尔可夫过程。因为这种无后效性, 也叫做马尔可夫性。所以, 本研究采用具有马尔可夫性的系统为研究对象的马尔可夫决策过程 (MDP) 来处理上述问题。
这里将要运用的离散时间MDP由5部分组成: { S, (A(i), i∈S), q, r, v}。其中S为状态空间, 它是被考察系统的一切可能状态的 (非空) 集, S={ 1, 2}。状态1表示林带结构与天气条件配合得好; 状态2表示林带结构与天气条件配合得不好。A(i) 为状态i可用的行动集, i∈S, A(1)={ b, c}, A(2)={ b, c}。q是系统状态的转移律族, 族的参数是可用的行动。假定q是时间齐次的马尔可夫律族。q(j/i, a) 表示:在任一时刻t(t=0, 1, 2, …) 系统处于i, 在选用行动a∈A(i) 的条件下, 于时刻t+1, 系统转移到状态j的概率, 它与系统在时刻t以前的历史无关, 也与时刻t无关。
令Г={r(i, a):a∈A(i), i∈S}, r是定义在Г上的单值实函数, 称为报酬函数。r(i, a) 表示在任一时刻t系统处于状态i选用行动a时所获得的报酬。
准则V是定义在Π×S上的单值实函数, 其中Π是全体策略集, S是状态空间。对任一给定的策略π∈Π, 状态i∈S, V(π, i) 表示t=0时从状态i出发的条件下, 用策略π的准则值。
根据给定的条件和观察结果, 可以写出:状态空间S={1, 2}, 每个状态可用的行动集A(1)=A(2)={b, c}; 转移概率: q(1/1, b)=0.52, q(2/1, b)=0.48, q(1/1, c)=0.81, q(2/1, c)=0.19, q(1/2, b)=0.41, q(2/2, b)=0.59, q(1/2, c)=0.72, q(2/2, c)=0.28;报酬:r(1, b)=6200, r(1, c)=4100, r(2, b)=-3100, r(2, c)=-5200。
如前所述, r(1, c)=4100。其意义是:林带结构与天气条件配合得好, 一年内本应获报酬 (气象增产值相应的经济效益毛收入) 6200元, 但由于选用行动c(疏透结构), 增加经济投入2100元, 故实际年报酬为6200-2100=4100元, 故r(1, c)=4100。余类推。
这里共有4个决策函数, 分别用f1, f2, f3和f4表示, 并可写出:
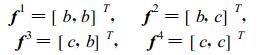
|
(1) |
就任一决策函数f∈F而言, 都有一个与之相对应的转移概率矩阵, 其形式为矩阵Q(fk) (k=1, 2, 3, 4), 该矩阵中的第 (i, j) 个元素为q(j/i, f(i)), i, j∈S。显然q(j/i, f(i)) 为非负的, 且每行各元素之和均为1。
对每个决策函数f∈F, 解线性方程组:
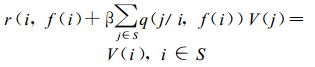
|
(2) |
其解为V(i)=Vβ(f∞, i), i∈S。
由此可以得到平稳策略f∞的折扣准则值列向量Vβ(f∞)。对所求的f∈F均这样做以后, 再一一进行比较, 就可以得到β最优平稳策略与最优值函数。因为在本研究中, 决策函数只有4个———f1, f2, f3, f4, 所以用上述穷举算法是可行的。
对线性方程组的解加以整理, 可以看出: V0.9(f4∞, 1)>V0.9(f3∞, 1), V0.9(f4∞, 1)>V0.9(f2∞, 1), V0.9(f4∞, 1)>V0.9(f1∞, 1) 及V0.9(f4∞, 2)> V0.9(f3∞, 2), V0.9(f4∞, 2)>V0.9(f2∞, 2), V0.9(f4∞, 2)> V0.9(f1∞, 2)。根据文献[6]给出的判断规则, 由以上不等式可以清晰地看出: V0.9(f4∞) 是最优值函数。由此可知:f4∞对于β=0.9而言为最优平稳策略。
用策略迭代算法来进一步求解这个问题———策略改进。
①首先任取一个决策函数, 取f1(从穷举算法可知, V0.9(f1∞) 是最差的折扣准则值列向量) 作策略求值运算。即求解线性方程组, 结果给出: V0.9(f1∞, 1)≈17332.60, V0.9(f1∞, 2)≈6690.18。按两步作策略改进运算, 结果表明:在V(2, a) 中, 也是a=c时达到最大, 故取策略g(2)=c。这样的g实为f4, 因此实现了策略改进。
②首先以f4代替f1, 对f4∞做策略求值运算, 即求解线性方程组, 结果给出:V0.9(f4∞, 1)≈23695.32, V0.9(f4∞, 2)≈13575.63。按两步作策略改进运算, 结果表明:在V2(2, a) 中, a=c时V2(2, a) 达到最大, 故取改进策略g(2)=c, 即g仍为f4。f4∞是无法再改进了。这样, 可以得出如下结论: V0.9(f4∞) 为最优值函数。f4∞为β=0.9时的最优平稳策略。这就是说, 在所研究的条件下, 总应采用透风系数为0.35的疏透结构的农田防护林带。
3 结论与讨论从以上的分析和计算结果可以看出:当折扣因子β=0.9时, 在所研究的条件下, 总应采用透风系数为0.35的疏透结构林带这一行动, 这才是最优策略。当然, 这是就一个区域内的一组具体调查结果作分析计算而得出的。这样的结果可用于类似生态条件下的其他地区。这里所说的相似, 主要指作物生育期气象条件 (尤其是风) 相似、农田防护林带结构相似、被林带保护的作物相似。
由于所讨论的生态控制系统是十分复杂的, 各个变量随机性很明显, 而反映这些随机性特征的数据并不十分完善, 所以用于计算数据的代表性和可比性受到一定限制。这有待在今后的工作中加以改进。
本研究只是防护林设计系统工程中可用的生态控制方法之一, 它是在生态控制原理基础上的一种尝试。实际上系统工程中的许多其他优化方法, 也可考虑被用于类似研究之中。随着MDP等一系列运筹学方法的不断进步, 有关的先进的数学方法将更加完善。作为气象生态工作者, 跟踪这些新的进展并及时结合生态控制问题构建相应数学模型, 以服务于生产实践, 是非常必要的。
致谢 本研究在调查、观测和资料整理方面, 得到沈阳市及辽宁省气象部门许多同志支持, 孙福义同志参加了观测工作; 关德新、张玉书研究员审阅本文手稿并提出有益的建议, 谨此一并致谢。| [1] | 张翼, 卫林. 林带迎风防护区中风速分布的模拟研究. 科学通报, 1985, 28, (13): 1015–1018. |
| [2] | 朱廷曜, 周广胜. 农牧防护林网区域性防风效应及评价模型. 林业科学, 1993, 29, (6): 509–514. |
| [3] | 朱廷曜, 关德新, 周广胜, 等. 防护林生态工程. 北京: 中国林业出版社, 2001: 314-332. |
| [4] | 贺庆棠. 中国森林气象学. 北京: 中国林业出版社, 2001: 98-117. |
| [5] | 王梓坤, 杨向群. 生灭过程与马尔可夫链. 北京: 科学出版社, 2005: 1-10. |
| [6] | 董泽清, 刘克. 伴有无界报酬的半马尔可夫决策规划的最优策略结构. 中国科学 (A辑), 1986, 29, (4): 337–349. |
| [7] | Lai K K, Liu K, Liu J Y. On dispaching unequally capable service technicians. Ima J Manag Math, 2002, 13, (2): 153–156. |
| [8] | Liu J Y, Liu K. Markov decision programming-the moment optimal problem for the first-passage model. J Australia Math (Soci ser B):Appl Math, 1997, 38, (4): 542–562. DOI:10.1017/S0334270000000850 |
| [9] | 刘克. 实用马尔可夫决策过程. 北京: 清华大学出版社, 2004: 16-31. |
| [10] | 裴铁璠, 于系民, 金昌杰, 等. 生态动力学. 北京: 科学出版社, 2001: 44-68. |
| [11] | 裴铁璠, 金昌杰, 关德新. 生态控制原理. 北京: 科学出版社, 2003: 218-222. |
| [12] | Pei T F, Jin C J, Guan D X. Ecologcal Dynamics and Cybernetic Principle. Monmouth Janctiion NJ: Science Press USA Inc, 2004: 110-125. |
| [13] | 路甬祥. 生态控制原理. 北京: 科学出版社, 2003: 1-2. |
| [14] | 关德新, 朱廷曜. 风阻抗能力与林带结构关系的理论分析. 北京林业大学学报, 1998, 20, (4): 119–121. |
| [15] | 关德新, 朱廷曜. 树木冠层结构参数与风场特征的风洞模拟研究. 应用生态学报, 2000, 11, (2): 202–204. |
| [16] | 钱学森, 于景元, 戴汝为. 一个科学新领域——开放的复杂巨系统及其方法论. 自然杂志, 1990, 13, (1): 3–10. |
| [17] | Hu X H. Hall for Workshop of Metasynthetic Engineering: Design Issues and an Example∥Proceeding of the ICSSSE. Beijing: Scientific and Technical Documents Press, 1998, 98(2): 234-249. |
| [18] | 王馥棠, 冯定原, 张宏铭, 等. 农业气象预报概论. 北京: 气象出版社, 1991: 447-452. |
| [19] | 刘建栋, 王馥棠, 于强, 等. 华北地区农业干旱预测模型及其应用研究. 应用气象学报, 2003, 14, (5): 593–604. |
| [20] | 刘布春, 王石立, 庄立伟, 等. 基于东北玉米区域动力模型的低温冷害预报应用研究. 应用气象学报, 2003, 14, (5): 616–625. |
| [21] | 王石立, 庄立伟, 王馥棠. 近20年气候变暖对东北农业生产水热条件影响的研究. 应用气象学报, 2003, 14, (2): 152–164. |
| [22] | 马玉平, 王石立, 王馥棠. 作物模拟模型在农业气象业务应用中的研究初探. 应用气象学报, 2005, 16, (3): 293–303. |
| [23] | Yu X M, Bi B J. Forecasting the distribution of meteorological yields using Chebyshev polinomils. Agric For Meteorol, 1985, 34, (3): 323–332. |
| [24] | Yu X M, Pen W B. Monte Carlo method for risk analyses of meteorological damages affecting the crop yields. Agric For Meteorol, 1988, 43, (2): 183–191. |
| [25] | 徐玖平, 胡知能, 李军. 运筹学. 北京: 科学出版社, 2005: 1-417. |
 2007, 18 (2): 242-246
2007, 18 (2): 242-246

