应用气象学报  2007, 18 (2): 187-192   PDF    
引用本文
唐国利, 丁一汇. 由最高最低气温求算的平均气温对我国年平均气温序列影响[J]. 应用气象学报, 2007, 18(2): 187-192.
Tang Guoli, Ding Yihui. Impacts of the Average Air Temperature Derived from Maximum and Minimum Temperatures on Annual Mean Air Temperatures Series of China[J]. Journal of Applied Meteorological Science, 2007, 18(2): 187-192  
由最高最低气温求算的平均气温对我国年平均气温序列影响
唐国利1,2,3, 丁一汇1     
1. 国家气候中心 中国气象局气候研究开放实验室, 北京 100081;
2. 中国科学院大气物理研究所, 北京 100029;
3. 中国科学院研究生院, 北京 100039
2005-11-11 收到, 2006-07-14 收到修改稿.
资助项目: 国家“十五”科技攻关项目“全球与中国气候变化的检测和预测”(2001BA611B-01) 和中国气象局气候研究开放实验室开放基金课题共同资助    
摘要: 针对研究全国近百年平均气温长期变化的实际需要，利用603个测站1961—2002年气温观测资料，比较分析了最高最低平均气温距平序列和4次观测记录平均气温距平序列的差异，讨论了最高、最低气温变化趋势。结果表明：两种统计方法得到的平均气温距平序列及增温速率的差异均不明显，在一定条件下两者可以互相替换。此外，最高、最低气温变化普遍存在不对称现象，且可分为4种类型，这种不对称性对平均气温变化速率并没有明确一致的影响。
关键词: 气温序列    最高最低气温    平均气温求算方法    
Impacts of the Average Air Temperature Derived from Maximum and Minimum Temperatures on Annual Mean Air Temperatures Series of China
Tang Guoli1,2,3, Ding Yihui1     
1. Laboratory for Climate Studies, National Climate Center, CMA, Beijing 100081;
2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. Graduate University, Chinese Academy of Sciences, Beijing 100039
Abstract: The global warming is one of the focuses to which greatly attention are paid by scholars, officials and the public in the world. And the global or regional surface air temperature changing trend is a key issue in the climate change detection and research. The mean temperature data which are derived from the 4 time observations per day are generally adopted in the research on climate change in China. But for the purpose of studying the long term mean air temperatures in the last 100 years in China, because the observation time is different and complicated, the observation time systems are not unified and the statistical methods for the mean temperature are inconsistent, severe inhomogeneity exists in the monthly mean temperature data before 1950. As a result, the inhomogeneity of the data brings down the reliability of the surface air temperature series, thus has influences on both the connection of air temperature series of different periods and the estimate of the long term temperature change trend. Especially it will severely affect the quality of China's last 100 year air temperature series. A feasible way to overcome this problem is to re calculate the mean temperature based on the average of maximum and minimum temperatures and form China's surface air temperature series and the estimation of warming extent from it. Its advantage is highly obvious. Using this method, the cause of the above mentioned inhomogeneity can be eliminated and the relevant error with it can also be avoided. Accordingly, the homogeneity and quality of China's surface air temperature series can be improved greatly. However, it will bring some questions as follows: Do the differences (or obvious differences) between the results (including the mean air temperature and its anomaly series of regional average) derived from the two different statistical methods exist? And the maximum and the minimum air temperature changes have obvious dissymmetry phenomena, which have been found in previous researches. Do the dissymmetrical changes affect new mean air temperature series and the accuracy of the estimate of the air temperature change rate over China? To answer these questions, and satisfy the practical need in researches on the long term surface air temperature change in the last 100 years in China, using air temperature data of 603 stations during 1961—2002, the differences between the two kinds of mean air temperature anomaly series, averaged from the maximum and the minimum temperatures and the 4 time observations respectively, are compared and examined, also, the maximum and the minimum temperature change trends are discussed for researching their impacts on the long term annual mean air temperature series over China. The results show that there are no remarkable differences between the two kinds of mean temperature anomaly series obtained separately by means of different approaches and between their temperature change rates. They can be replaced by each other under certain conditions. In addition, the dissymmetrical phenomena of the maximum and the minimum air temperature changes are ubiquitous in China. And they may be classified into four types according to the features of the temperature changes. However, the impacts of dissymmetry on the mean air temperature change rates are uncertain.
Key words: air temperature series     maximum and minimum temperatures     calculations of mean air temperature    
引言

当前正在经历的全球气候变暖是一个国内外各界都非常关注的热点问题。在与此相关并具有重要意义的气候变化检测研究中, 分析全球和区域的气候变化事实并给出相应的温度变化率是一项非常重要的基础性课题。对于近百年来的全球地面温度变化来说, IPCC第三次评估报告给出了全球平均温度大约上升了0.6 ±0.2 ℃的估计[1], 这反映出全球气候变暖的趋势和程度。对于研究区域性的变化问题譬如中国的气候变化来说, 分析器测时期的温度变化并给出相应的变化速率也具有同样的重要性。在目前国内的相关研究工作中, 基础资料大多直接采用载于气象报表的平均温度资料。这样做, 对于分析近40余年的温度变化来说是恰当的, 但是如果研究近百年的变化则会在序列均一性上出现比较严重的问题。这是由于我国解放前的气温观测资料纷繁复杂、情况多样, 例如仅观测时次就达20余种, 加上观测时制变化和平均气温统计方法不统一等因素, 导致资料序列存在严重的非均一性。这种非均一性一方面大量存在于1950年以前的资料序列中, 同时还造成解放前后气温序列的可比性差, 严重影响到我国百年气温序列的整体质量。这也一直是困扰器测时期温度变化研究的主要问题之一。为了适应气候变化研究的不断深入和发展, 满足国家和社会的需要, 提高全国平均气温序列的准确度和可信度自然就成为一个迫切需要解决的问题。所幸的是, 在我国长期器测记录中, 最高和最低温度一般是比较完整的, 因而可以利用这部分资料作为解决上述问题的一条新途径。通过最高最低气温求算平均气温并在此基础上计算新的我国地面平均气温序列及新的增温估计值, 借此方法可以消除产生上述非均一性的根源、避免由此产生的误差, 从而可在很大程度上改善我国地面气温序列的均一性。文献[2]已在这方面做了初步尝试。然而采用这种平均气温求算方法得到的结果与通常采用的平均气温及其区域平均距平序列是否存在差异或明显差异?而且根据以往的研究, 最高、最低气温的变化存在非对称性[1], 那么这种非对称性是否会对新的平均气温序列产生影响?是否会影响对温度变化率的估计?这些问题都需要通过相关研究予以回答。同时这些问题对研究我国近百年来的温度变化也具有十分重要的现实意义。

计算平均气温的方法有许多种, 例如3次观测平均、4次观测平均、8次观测平均、24次观测平均和最高最低记录平均等等。按照我国气象部门现行的地面气象观测规范的规定, 国家基准站和基本站日平均气温的求算须根据北京时间02:00, 08:00, 14:00, 20:00共4次定时观测的温度记录计算平均值。这就是目前我国气象业务和科研工作中普遍采用的平均气温。统计事实表明, 不同计算方法所得平均气温之间存在着一定差异。就最高最低气温统计得到的平均气温与4次观测记录的平均气温而言, Miller[3]曾指出, 最高最低平均得到的平均气温普遍高于定时观测得到的平均气温。叶芝菡等[4]曾利用全国8个气象站的温度观测资料对两种平均气温的差异进行了比较, 认为两者差异显著, 但基本无年际间的变化。为了进一步验证全国的情况, 本研究利用603个测站的观测资料按最高最低气温平均得到新的年平均气温并与4次观测平均气温比较后发现, 虽然两种平均气温的差值正负皆有, 但无论从站点数量还是出现年份看, 正差值都占绝对优势。按30年的平均气温比较, 全国除个别站4次观测平均值高于最高最低平均值以外, 其余绝大部分站最高最低平均值均高于4次观测平均值, 其偏差范围在-0.13~1.77 ℃之间, 全国平均偏高0.57 ℃。然而, 由于研究和关注的重点是我国气温的变化特征及估计气温变化速率, 而这种变化可由气温距平反映出来, 由此便有可能减小或消除上述偏差可能产生的影响。本文主要针对全国平均最高最低平均气温距平序列与4次观测平均气温距平序列及相应的温度变化速率进行对比分析。同时, 也对全国最高、最低气温变化趋势的一些特点进行了分析和讨论。

1 资料和方法

气温观测资料由国家气象信息中心气象资料室整编并提供。为了确保可比性, 首先按照序列长度一致的原则, 取603个气象站1961—2002年的逐月平均气温、平均最高气温和平均最低气温资料。除其中的标准4次观测平均气温外, 又由月平均最高、最低气温计算月平均气温, 进而分别得到两种计算方法下的年平均气温。本文主要针对上述两种年平均气温进行分析。

为了叙述方便, 文中将4次观测记录平均得到的平均气温记为T4; 最高、最低气温平均得到的平均气温记为Tmn; 平均最高气温记为Tm; 平均最低气温记为Tn。相应的气温变化速率在上述符号的下标处加英文小写字母r表示, 如T4r, Tmnr, Tmr和Tnr等。

在估计温度的变化速率时, 以一元线性方程对原序列y进行拟合, 即

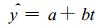
(1)

其回归系数b反映了气温的趋势变化, 即

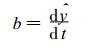
(2)

式 (1) 和 (2) 中t表示时间, b表示气温变化速率, b×10表示气温每10年的变化。

在计算全国平均气温序列时, 首先对各测站气温做距平化处理, 其中气候参考值取1971—2000年的平均值。然后分别采用算术平均和按纬度面积加权平均[5]的方法, 得到两个全国平均气温距平序列 (以下的全国平均气温序列均指距平序列)。

2 Tmn与T4序列及其变化速率的比较

对于气候变化研究来说, 关注的重点主要是气温的年际、年代际变化以及某一时期的变化趋势。虽然Tmn普遍高于T4, 但是经过距平化处理和区域平均之后所得到的Tmn序列却未必如此; 那么解答它与T4序列的差异如何以及是否适用等问题是本研究的主要目的之一。因此就需要对两种全国平均气温序列进行对比分析, 从而确定Tmn序列的适用性。这里, 两个平均序列变化速率的差值可被看作一随机变量, 当取不同数量的测站时, 相应的区域平均序列变化速率的差值也会发生一定变化。因此, 需要首先分析差值的分布及其取值区间问题。分别计算603个测站Tmn和T4的变化速率及其差值, 绘制全国分布图 (图略) 可见, Tmn和T4变化趋势的全国分布大体一致; 两者变化速率差值的空间分布整体上比较散乱, 没有表现出明显的规律性。经统计, 差值≥0的站点数略多, 为336个, 差值 < 0的站点为267个, 分别占总站数的55.7 %和44.3 %。差值范围在-0.1696 ℃/10 a~0.1371 ℃/10a之间, 平均为0.0067 ℃/10a。其中, 气温变化速率差值的全国平均值由式 (3) 计算。

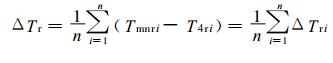
(3)

式 (3) 中, i表示测站序号, n为测站总数。

由简单的数学推导可知, 可以通过分析参加统计的所有站点差值的平均值来估计全国平均序列气温变化速率的差值及其置信区间。即估计两个全国平均序列变化速率的总体差异实际上可以转化为估计多站点平均差值的取值区间问题, 也就是温度变化速率平均差值的区间估计。

设X为服从正态分布的随机变量, 根据概率统计理论, 其数学期望E(X) 的置信区间为

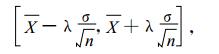
其中X为样本平均值, σ为样本标准差, n为样本容量, λ是t分布的临界值。运用上式, 不仅可以估计服从正态分布的随机变量期望的区间, 而且当样本容量n相当大时, 也可对任意分布的随机变量的E(X) 进行比较准的估计。这是因为, 根据概率论中的中心极限定理, 无论X是怎样的随机变量, 只要n充分大, 就可认为随机变量

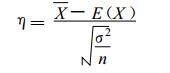
(4)

遵从标准正态分布。因此, 当站点数量较多 (通常大于50) 时, 无须考虑变化速率差值的具体分布形态就可对其期望进行估计。就待解决的实际问题而言, 当测站数取603时, 两种统计方法得到的温度变化速率差值平均值95 %的置信区间为[0.0036 ℃/10a, 0.0098 ℃/10a]。对于更多或更少的站点来说, 也可用同样的方法得到相应的取值区间。考虑站点数量相对较少的情况, 随机抽取10, 20, 30和40个站点, 经计算偏度和峰度在信度取α=0.05的标准下, 变化速率的差值均近似服从正态分布。以10个站点的情况为例, 平均值95 %的置信区间为[-0. 0166 ℃/10a, 0.0360 ℃/10a]。假设由此推算到100年, 当测站数分别取603和10时, 由两种统计方法得到的气温变化速率差值的取值范围分别为0.036~0.098 ℃/100a和-0.166~0.360 ℃/100a, 可见前者的差异仍然非常小, 而后者的差异稍大一些。

计算区域平均序列时, 通常视具体情况来决定采用算术平均或面积加权平均等统计方法。为了便于比较, 这里分别应用上述两种方法计算603站的两种 (T4和Tmn) 全国平均气温距平序列。其气温变化速率及差值见表 1。从中可见, 由第一种方法得到的T4和Tmn序列给出的全国平均增温率比第二种方法大约低0.034 ℃/10a左右, 这反映了不同区域平均方法的影响。非常明显的是, 虽然两种区域平均方法得出的增温速率存在一定差异, 但T4序列和Tmn序列增温速率的差值却十分接近, 分别为0.0065 ℃/10a和0.0067 ℃/10a。可见, 无论采用哪种区域平均方法, 由Tmn序列得出的全国气温变化速率与T4序列的差异均很小。这种差值比增温速率本身低两个数量级, 相对偏差仅2.5 %左右。另据前例可知, 即使仅取10个测站求取平均值时, Tmn与T4变化速率的差异仍然比增温速率的估计值小1个数量级。

表 1 两种平均气温的平均变化速率及差值 (单位: ℃/10a) Table 1 The change rates and their difference of two kinds of mean temperatures in China (unit : ℃/10a)

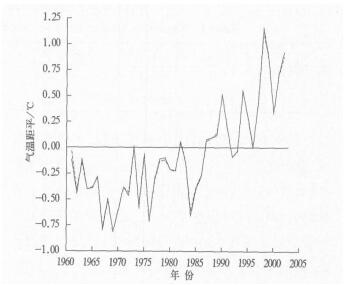
因此, 可以认为两者的差异不明显并且与区域平均方法无关。即从气温变化率的角度来看, 在一定条件下以全国平均Tmn序列代替T4序列不会对温度变化速率的估计值产生明显影响。也就是说, 对于研究和估计全国平均气温变化来说, 只要保证一定的测站数量, 则以Tmn得到的结果与T4十分接近。另一方面, 如果从全国平均序列本身看也会得到相似的结果。事实上, 虽然Tmn高于T4, 但是Tmn距平序列的数值以及年际变化和年代际变化与T4距平序列均没有明显差异, 两者的相关系数高达0.999, 图 1也直观地表明了这一点。因此, 可以在相当高的精度下用Tmn序列代替T4序列。

图 1. 1961—2002年全国平均Tmn(实线) 和T4(虚线) 距平曲线 Fig 1. Average Tmn(solid line) and T4 (dashed line) anomalies in China during 1961—2002

3 关于最高最低气温变化趋势的一些讨论

观测事实表明, 近100年和近50年来的全球气候变暖, 最低气温和最高气温的变化并不同步。最突出的表现是近50年来最低气温增温速率明显高于最高气温。据IPCC第三次评估报告[1]给出的数据, 自20世纪50年代以来, 全球陆地有资料地区最低气温的增温幅度约为最高气温增温幅度的2倍。这就是一般所说的最高、最低气温增温的不对称性, 这种现象说明近几十年的气候变暖过程中夜间的增温贡献更大。由此容易从直观上认为, 因这种不对称性的影响, 利用最高最低气温得到的平均气温序列, 其增温速率必然会高于T4序列的增温速率。那么实际情况是否一定如此呢?下面就我国近40年来最高、最低气温变化趋势的一些特点及上述问题进行分析和讨论。

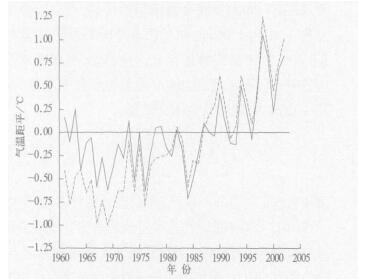
从全国平均来看, 1961—2002年间最高气温Tm约升高0.81 ℃, 最低气温Tn约升高1.63 ℃, 后者增温幅度约为前者的2.01倍, 这与全球陆地平均状况相当接近。分别绘制全国平均Tm和Tn距平曲线 (图 2) 并仔细分析其变化特点后发现, 在20世纪70年代中期以前, Tm与Tn的较差相对较大, 且两者呈相反的变化趋势, 分别为下降和上升。此后, Tm与Tn的较差变小, 且两者均呈上升趋势, Tn的增温速率略高于Tm, 两者的速率差异明显小于前一阶段 (见表 2)。这种Tm与Tn在前后两段的较差及变化速率的差异, 反映在全时段的增温率上, 就表现为Tn增温率远高于Tm。这说明, 近40年来的Tnr明显高于Tmr除与后期增温率的差异有一定关联外, 前期的较差偏大也是一个重要原因。为了进一步说明平均温度变化是否受到这种变化的影响, 将序列以1981和1982年为界划分为前后两段。从表 2可以看到, 1961—1981年期间, Tn的上升速率明显高于Tm, 这说明平均温度升高主要是由Tn上升引起的, 这一时期Tmn的增温幅度比T4高0.04 ℃; 但1982—2002年, Tn与Tm的变化速率十分接近, 两者近乎同步上升, 而该时期Tmn的增温幅度仍比T4高0.038 ℃。这从另一侧面说明, Tn与Tm的变化对Tmn序列变化率的影响具有一定的复杂性。

图 2. 1961—2002年全国平均Tm (实线) 和Tn (虚线) 距平曲线 Fig 2. Average Tm (solid line) and Tn (dashed line) anomalies in China during 1961—2002

表 2 全国平均最高、最低气温的变化速率 (单位: ℃/10a) Table 2 The change rates of maximum and minimum air temperature in China (unit : ℃/10a)

对于全国各测站的变化趋势来说, 可以根据最高、最低气温变化速率的组合情况, 将其划分为4种类型 (表 3)。其中Ⅰ型的最高、最低气温均呈上升趋势, 此型内又可依据Tnr与Tmr的相对大小分为两种情况。全国属于这种类型的约占84 %; Ⅱ型的最高、最低气温变化趋势相反, 即Tm下降, Tn上升, 这种类型约占12 %; Ⅲ型的最高、最低气温变化趋势也相反, 但Tm上升, Tn下降; 出现最少的是Ⅳ型, 即最高、最低气温均呈下降趋势。后两种类型所占比例极小, 两者相加不足4 %。由此可见, 最高、最低气温的非对称性变化是一种普遍现象, 最高、最低气温变化趋势的不同组合与ΔTri(最高最低气温求算所得平均气温增温速率与4次观测平均气温增温速率间的差值) 之间没有明确一致的对应关系。例如, 同样属于Ⅰ型, 在Tnr, Tmr均大于0且Tnr > Tmr的情况下, 虽然有247站的ΔTri大于0, 但同时仍有174站的ΔTri < 0。这表明, 最低气温增温速度快于最高气温的事实并不意味着Tmn的增温速率必然会高于T4的增温速率。因此, 综合考虑全国平均和各测站的情况后可以认为并不能确定Tm与Tn的不对称性变化对平均气温增温速率有明确一致的影响。

表 3 最高、最低气温变化趋势的组合类型及Tmnr与T4r的比较 Table 3 The types of maximum and minimum air temperature change trends and the comparison between Tmnr and T4r

4 结论与讨论

1) 就区域平均气温序列而言, 分别以最高最低气温平均和4次观测记录平均所得到的气温序列, 其长期变化趋势以及其年际变化和年代际变化均没有明显差异, 两者的气温变化速率差异也很小。因此对于研究和估计全国平均气温变化来说, 只要保证一定的测站数量, 就可以在相当高的精度下用Tmn序列代替T4序列, 因而全国平均Tmn序列及其增温率是可信的。

2) 近40年来, 全国平均最高、最低气温存在明显的非对称性变化, 后者增温幅度约为前者的2倍多。这与前期的差值大有很大关系。从全国各测站的变化来看, 最高最低气温的非对称性变化是一种普遍现象, 但存在4种类型。同时, 观测事实也表明最低气温增温速度快于最高气温并不意味着Tmn的增温速率必然高于T4的增温速率, 也就是说并不能确定最高气温与最低气温的不对称性变化对平均气温变化速率有明确一致的影响。

参考文献
[1] Houghton J T, Ding Y, Griggs D J, et al. Climate Change 2001:The Scientific Basis. Cambridge: The Press Syndicate of Cambridge University, 2001: 1-881.
[2] 唐国利, 任国玉. 近百年中国地表气温变化趋势的再分析. 气候与环境研究, 2005, 10, (4): 792–798.
[3] Miller A A. Climatology. London: Methuen & COLTD, 1950.
[4] 叶芝菡, 谢云, 刘宝元. 日平均气温的两种计算方法比较. 北京师范大学学报 (自然科学版), 2002, 38, (3): 421–426.
[5] Jones P D, Hulme M. Calculating regional climatic time series for temperature and precipitation:methods and illustrations. Int J Climatol, 1996, 16: 361–377. DOI:10.1002/(ISSN)1097-0088