2. 上海中心气象台, 上海 200030;
3. 上海气象影视中心, 上海 200030
2. Shanghai Meteorological Center, Shanghai 200030;
3. Shanghai Center of Meteorological Audio & Video, Shanghai 200030
气候变化对经济和社会发展的影响, 已成为当前各国政府和科学家们所关注的重大问题。为研究细致的区域气候变化, 人们常常应用耦合GCM的中尺度数值模式来模拟区域气候, 从而得到给定地区的气候变化特征。国内外学者做了大量相关研究[1-3], 结果表明:区域气候模式具有较好的模拟能力。但区域模式的侧边界条件定解问题, 在理论和实际预报中, 都有大量尚需解决的问题。有限区域气候模式与短期天气预报模式相比, 还存在其特殊的难点, 即侧边界误差在长时间积分中的积累问题。为了解决区域气候模式侧边界问题, 其侧边界过渡区往往取得很宽, 几乎占全部积分区域的50%以上; 当垂直方向分辨率加大时, 水平圈数也加大。
Anthes[4]指出:大模式存在预报波下限为8倍模式网格距, 因而其对较大尺度波的预报较好。与大模式预报不同, 有限区域模式不仅存在可预报波下限, 还存在可预报波上限。黄丽萍等[5]对侧边界误差做了较为详细的分析, 认为在有限区模式中, 许多物理量的误差分布在上层, 如感热场、水汽场等。根据大小模式各自优势及嵌套误差主要集中在中高层这一结论, 可将有限区域模式不仅在水平侧边界与大模式嵌套, 而且在垂直方向的上边界也以某种方式与大模式嵌套, 这即为三维嵌套。赵俊英[6]做了相关研究, 认为三维嵌套在技术上可行, 模式亦运行稳定。徐传玉等[7]采用三维嵌套方法对1990年8月1日华北暴雨过程进行了数值模拟, 结果令人振奋。本文在前人研究基础上实现了三维嵌套长时间积分的稳定运行, 为改善有限区域气候模式侧边界问题提供了有益的探索。
1 模式及方案设计本文采用颜宏[8]设计的“复杂地形条件下嵌套细网格模式”(YH模式), 模式采取单向影响嵌套边界, 在水平结构上取C型跳点网格。为了兼取p坐标和σ坐标的优点, 并考虑到行星边界层的特点, 采用了等厚行星边界层的p-σ混合坐标系, 垂直方向上分为6层。
三维嵌套设计基本思路是在模式大气上层 (若干层) 引入大模式资料, 再加入强对流订正。若以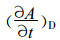
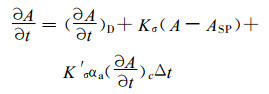
|
(1) |
式 (1) 中, A为小模式预报量 (包括u, v, T, q); ASP为大模式预报量 (包括u, v, T, q); 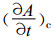
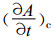

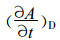
|
|
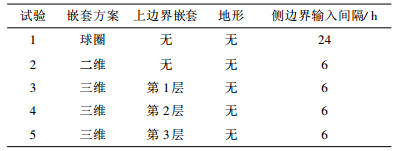
表 1 实验方案设计 Table 1 Test design |
2 结果分析 2.1 高度场分析
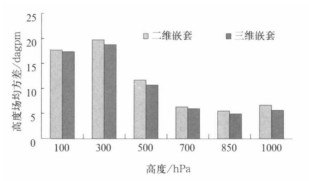
图 1为试验2与试验4高度场模拟期平均的均方差比较。在引入球圈模式第2层资料后, 试验4各层方差都比试验2小, 在低层改进尤为明显。其中850 hPa及1000 hPa高度场模拟期平均均方差均超过了10%, 500 hPa高度场模拟期平均均方差也超过了8%。而试验3和5效果较试验4差 (图略), 由此并非所有高层资料的引进就能提高预报能力。在本文中, 引入大模式第2层即300 hPa资料是合适的。以下若无特殊说明, 三维嵌套均指试验4之结果。
|
|
| 图 1. 40 d平均高度场均方差 Fig 1. Forty-day average height field mean square deviation | |
表 2为高度场旬平均各等压面均方差。前10 d积分中三维嵌套在500 hPa层次以下改进较为明显, 但以上层次则不尽然。在随后的模拟中, 三维嵌套的作用开始逐渐显现, 所有层次三维嵌套方差均小于二维嵌套方差, 尤其在高层与积分初期相比有明显改进。
|
|
表 2 高度场旬平均各等压面均方差 (单位:dagpm) Table 2 Ten-day average height field mean square deviation of each isobaric chart (unit:dagpm) |
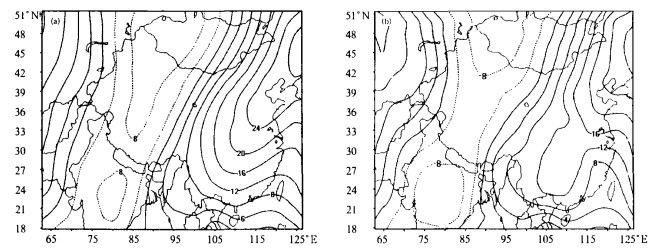
图 2为两方案与参考场模拟期平均500 hPa高度场偏差。两者均有偏差值由北向南递减的共性, 在预报区域的东部, 三维嵌套的偏差值明显比二维嵌套小。在95°E以东, 42°N以南的范围内, 三维嵌套明显较二维嵌套好。以等值线20 dagpm为例, 图 2a的20 dagpm等值线最南到29°N左右, 而图 2b的该等值线最南到34°N, 比二维嵌套北移了约5个纬度, 与参考场更为接近。
|
|
| 图 2. 模拟期40 d平均500 hPa高度场偏差 (单位:dagpm) (a) 二维嵌套, (b) 三维嵌套 Fig 2. Simulation forty-day average 500 hPa height field discrepancy (unit:dagpm) (a) two dimensions nesting, (b) three dimensions nesting | |
2.2 不同嵌套对风场的影响
表 3为u, v场40 d平均在各等压面均方差表。对u场而言, 100 hPa以下各层次三维嵌套结果均优于二维嵌套, 但100 hPa层次不如二维嵌套; 而v场则在各个层次都得到改进, 100 hPa等压面上改进率接近5%, 比u场效果更好。
|
|
表 3 u, v场40 d平均各等压面均方差 (单位:m/s) Table 3 Forty-day average u, v field mean square deviation of each isobaric chart (unit:m/s) |
2.3 模式稳定性
在本模式中以动能及地面气压倾向均方根值作为判断模式运行是否稳定的依据。图 3为两方案的动能曲线。对试验2而言, 在预报前4 d, 动能呈衰减之势, 随后振荡攀升。而试验4在积分初期, 动能有所增加, 积分中期相对稳定, 随后动能缓慢增加, 但增幅小于试验2。而试验2与试验4的位势拟能都较平稳, 均无大幅振荡的现象, 其位势拟能守恒 (图略), 模式采用三维嵌套方法在长时间积分中能稳定运行。

|
|
| 图 3. 模拟期动能曲线 Fig 3. Simulation momentum curve | |
2.4 诊断量比较
作为判断方案优劣的指标, 本文对两方案大尺度降水、水汽通量等诊断量进行对比, 其详细推导见文献[5]。嵌套方案预报量为M1, 球圈模式预报量为M0。令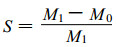
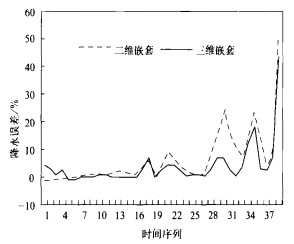
从图 4看出, 针对大尺度降水试验4明显优于试验2。尤其在第10—16天时段, 试验4模拟结果几乎与参考场重合, 随着积分时间的增长, 两种方案的误差率都有不同程度的增加, 这可能与模式本身及预报所用资料有关。在长时间积分中, 水汽预报在边界上层流出区嵌套误差较大。而试验4水汽通量误差率极值远小于试验2;就整个积分时段而言, 试验4在积分后半时段优势较为明显 (图略)。
|
|
| 图 4. 大尺度降水内区误差比率 Fig 4. Error ratio of large-scale precipitation at inner region | |
3 讨论
本文利用球圈模式进行模式自嵌套, 以球圈模式为参考场, 对二维嵌套和三维嵌套长时间积分结果做了初步研究, 得到如下几点结论:
1) 三维嵌套方案中, 大模式嵌套资料的选取非常重要; 只有适当层次资料的引入才能起正面作用。
2) 模式采用三维嵌套方法在长时间积分中能稳定运行。
3) 三维嵌套方案在长时间模拟中优于二维嵌套, 且积分时间越长, 效果越明显。
需要指出的是, 在初步的试验中没有对大模式资料做更多的处理, 这可能是造成积分初期高层模拟不甚理想的原因。如果考虑倾向嵌套, 即在垂直方向将大模式资料引入时, 设一张弛区, 既注意了模式的协调性, 又引入了良好的资料。这与水平方向嵌套原理是一致的, 需要在今后的工作中做进一步研究。
| [1] | 刘一鸣, 丁一汇, 李清泉. 区域气候模式对中国夏季降水的10年回报试验及其评估分析. 应用气象学报, 2005, 16, (增刊): 41–47. |
| [2] | 李巧萍, 丁一汇. 区域气候模式对东亚冬季风多年平均特征的模拟. 应用气象学报, 2005, 16, (增刊): 30–40. |
| [3] | Giorgi F, Marrinuci M R, Bates Gary T. Development of a second-generation regional climate model (RegCM2).Part Ⅰ:boundary-layer and radiative transfer process. Mon Wea Rev, 1993, 121: 2794–2813. DOI:10.1175/1520-0493(1993)121<2794:DOASGR>2.0.CO;2 |
| [4] | Anthes R A. Review:regional models of the atmosphere in middle latitudes. Mon Wea Rev, 1983, 111: 1306–1335. DOI:10.1175/1520-0493(1983)111<1306:RMOTAI>2.0.CO;2 |
| [5] | 黄丽萍, 颜宏, 赵俊英. 区域气候模拟中侧边界嵌套误差的研究. 应用气象学报, 2004, 15, (2): 152–161. |
| [6] | 赵俊英, 颜宏. "三维嵌套"方案的设计及试验结果分析∥台风、暴雨灾害性天气预报技术研究成果汇编.北京:气象出版社, 1995:89-93. |
| [7] | 徐传玉, 颜宏.对一次华北暴雨过程的三维嵌套数值模拟∥华北地区中尺度暴雨试验论文集.北京:气象出版社, 1992:194-208. |
| [8] | 颜宏. 复杂地形条件下嵌套细网格模式的设计 (一) 数值模式的基本原理. 高原气象, 1987, 6, (2): 1–62. |
 2007, 18 (1): 124-128
2007, 18 (1): 124-128