应用气象学报  2006, 17 (2): 240-244   PDF    
引用本文
丑纪范, 任宏利. 数值天气预报———另类途径的必要性和可行性[J]. 应用气象学报, 2006, 17(2): 240-244.
Chou Jifan, Ren Hongli. Numerical Weather Prediction———Necessity and Feasibility of an Alternative Methodology[J]. Journal of Applied Meteorological Science, 2006, 17(2): 240-244  
数值天气预报———另类途径的必要性和可行性
丑纪范1,2, 任宏利1,2,3     
1. 兰州大学大气科学学院, 兰州 730000;
2. 中国气象局培训中心, 北京 100081;
3. 国家气候中心 中国气象局气候研究开放实验室, 北京 100081
2005-11-28 收到, 2006-01-05 收到修改稿.
资助项目: 国家自然科学基金项目40575036和40135020共同资助    
摘要: 通过讨论省 (甚至地、市) 气象部门要不要开展数值天气预报工作的问题, 认为不是所有的地方都要开展, 只是那些希望搞科研型业务、迫切要求提高当地高影响天气的预报准确率的地方要开展。对于如何开展的问题, 提出不是去重复类似于主流途径的做法, 而是开辟另类途径, 并阐述了另类途径的内容、方法和意义。强调开展另类途径无需构建模式 (这是非常困难的工作), 只需运转现成的模式, 借助所关心的现象的历史数据来改造现成模式, 使之本地化, 是完全可行的。
关键词: 数值天气预报    反问题    模式    
Numerical Weather Prediction———Necessity and Feasibility of an Alternative Methodology
Chou Jifan1,2, Ren Hongli1,2,3     
1. College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000;
2. China Meteorological Administration Training Center, Beijing 100081;
3. Laboratory for Climate Studies, National Climate Center, CMA, Beijing 100081
Abstract: The motivation of the study is to discuss the issue whether numerical weather prediction should be practiced in the meteorological departments at provincial, regional or city levels. It suggests that numerical weather prediction need not be operated by meteorological departments at all levels, and only need to be done by those who carry on scientific-research and urgently expecting to improve the accuracy of local high-impact weather prediction. With respect to the problem how numerical weather prediction should be put into practice, it is put forward that local meteorological departments are not fit for repeating those approaches originated from mainstream opinions, but should break a new path such as an alternative methodology. Furthermore, the content, method and meaning of such an alternative methodology are examined. The inverse problem that the information of historical data including analogue is made full use of estimating model errors is raised and an analogue errors correction method is theoretically introduced in order that one can combine effectively both statistical and dynamical methods together, and need not change the current numerical prediction models. The new alternative methodology not only adequately utilizes dynamical achievements but also can rationally extract the information of a great many analogues in historical data so as to reduce model errors and improve forecast skills. This prediction strategy can overcome the limitation of only using initial values in traditional numerical models on one hand, and on the other hand, is able to realize the pertinence of numerical model prediction for specific elements through the process of selecting their corresponding analogues. Theoretical analyses show that based on analogue correction method of errors, the conventional problem of numerical weather prediction may be transformed into the prediction problem of forecast errors. That is to say, the unknown error terms in current prediction can be mathematically estimated by means of the forecast error fields generated from historical analogue data similar to the current prediction initial values. Some related preliminary experiment results on a complicated atmospheric prediction model have documented the feasibility and validity of this method based on such alternative methodology. As are seen in related studies, in such an alternative methodology as analogue correction method of errors, it emphasizes that it is unnecessary to construct new numerical prediction model which is very difficult for local meteorological departments. In such circumstance, one only needs to operate the existing models and modify them in order to localize by using historical data associated with interesting phenomena. There for it is completely feasible in practice and has operational future. Of course, so far the selection process of historical analogues is still coarse, and especially, as to the problem how the unknown error terms in current prediction can be estimated using the forecast errors from historical analogue data requires much more work, and further researches are still needed.
Key words: numerical weather prediction     inverse problem     model    
引言

数值天气预报已经取得很大成功, 现在要开展定时、定点、定量预报, 只有依靠数值预报方法, 别无它途[1-3]。但当前数值预报的模式并不能满足各地日益增长的提高预报准确率的要求。一个数值模式如果要准确预测各地不同的现象, 必定需要准确反映各种不同现象的特征, 这就相当于寻找包治百病的良方而非特效药, 正如地图要完全准确反映地球表面的各种特征一样, 是不可能做到的。因此, 模式向多元化发展、使之具有针对性, 显然要求各地应广泛开展数值预报, 而不能由中央搞一个模式来解决所有问题。但如何开展呢?

当前数值模式发展的主流途径是不断提高分辨率, 更加逼真地描述各种物理过程, 走精细化道路[3]。因此, 各地如按主流途径的思路和方法建立适合于当地特点的模式 (特效药) 固然很好, 但客观上不现实, 目前只能在理想的方案和能够实现的方案之间找到平衡点。省 (地、市) 气象部门开展数值预报不宜遵循主流途径, 以免造成资源和人力的浪费。事实上, 各地预报员的统计经验性预报的依据是积累的关于当地该现象的大量实况资料, 这些资料在作为初值问题而提出的数值预报中未能利用。两者结合 (类似于中西医合疗) 的科学问题, 就是将历史数据应用到数值预报中去[4-24], 意味着要改变数值模式预报中仅使用初值的缺陷, 这正是数值模式具有针对性的关键所在。省 (地、市) 气象部门开展数值预报正是做这件事, 即致力于发展另类途径, 这是需要各地根据自身状况来做的。

其实, 对于数值预报中使用历史数据的做法, 国外也已存在, 例如超级集合中根据各模式历史回报情况对预报结果进行加权平均, 以及对模式预报结果进行的各种统计性和经验性误差订正技术等等。但要从源头上进行集合或者误差订正, 就必须将外在使用历史数据转变为内在使用, 变初值问题为反问题, 对不同模式的预报误差进行预报、估计并订正, 使它们的结果趋于一致①[25], 这与国外的做法存在本质区别。

① 丑纪范.怎样使发布的短期气候预测更准确？———原来有捷径可走！中国气象局国家气象中心特邀报告. 2004年2月16日.

1 另类途径的内容、方法和意义

数学上, 数值预报模式一般可以表示为

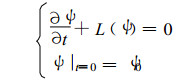
(1)

式 (1) 中, L为表征模式的算子, ψ为模式变量, 记P (ψ) 为模式变量的泛函。那么, 按照主流途径进行模式的一系列改进, 就可以表示为

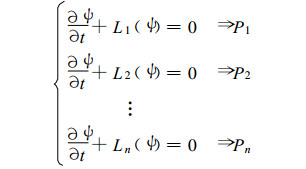
(2)

式 (2) 中L1, …, Ln表示数值模式发展的不同版本, 对应地, P1, …, Pn代表预报的物理量, 伴随着模式的不断改进, 我们自然期望预报的量P逐渐接近实际观测。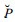

近年来, 观测资料精度和模式性能不断得到改善, 而预报准确率提高缓慢。由此可见, 即便各地都发展自己的模式, 能否显著提高预报准确率仍是未知数。面对各地日益增长的提高预报准确率的要求, 一个数值模式如果要准确预测各地不同的现象, 必定需要模式能够准确描述各种不同现象的特征, 这如同寻找包治百病的良方, 是行不通的。正如引言中所述, 使模式具有针对性, 向多元化发展, 客观上要求各地广泛开展数值预报, 但却不能再重复主流途径的做法, 应寻找更为有效实用的另类途径———将历史数据应用到数值模式的预报中去, 既能克服数值模式仅使用初值的缺陷, 又使模式预报具有针对性。

1.1 估计模式误差的反问题

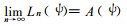
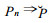
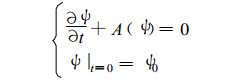
要充分利用物理规律 (动力学的成就), 莫过于以动力模式作基础。至于动力模式对实际过程描述的误差信息, 就蕴涵在过去的实况资料中。对于式 (2) 中主流途径的模式发展过程, 完全可以换个角度来看:当, 则有, 其中A为真实大气所满足的准确模式, 可以表示为

(3)

可以想象, 这就是当前数值模式发展的终极目标。不妨设A (ψ)-L (ψ)=E (ψ), 则式 (3) 可进一步变为

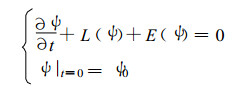
(4)

式 (4) 中, E为未知的误差算子, 表征实际存在而在式 (1) 中未能描述或准确描述的过程, 它所反映的正是实际数值模式中未知的误差项。那么, 我们所掌握的观测资料就是满足式 (3) 的一系列特解或者特解的泛函。由于式 (4) 有了未知项, 只有增加另外的信息才能求解, 另外的信息从何而来？这要从实况观测资料而来。事实上, 要充分利用气候统计学研究气候系统过去行为所揭示的规律, 关键在用动力学的观点来看待积累的实况观测资料, 即实况资料可以看作是描述气候系统的动力模式, 在增加了一个未知项而成为准确模式后的一系列特解, 由此可见, 方程中未知项的信息包含在方程的一系列已知的特解 (观测资料) 中。

因此, 如果我们改变问题的提法, 将初值问题提为一种反 (逆) 问题, 就有望将模式只用初值的缺陷和没有针对性的问题一并解决。从方法论上, 如果已知微分方程中的各项和参数来求取方程的解, 就是通常所说的正问题; 而如果微分方程的解已知, 反过来确定方程中的一些未知项或参数, 就是所谓的反 (逆) 问题。实际问题大多属于反问题。因此, 需要改变对预报问题的提法:由微分方程的初值问题转化为求解微分方程的反问题。

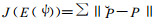
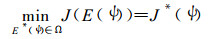
解反问题的通常方法是: 依据实况历史资料提供的众多特解, 估计出式 (4) 中的未知项, 然后再解正问题。首先, 依据专业知识构造函数类Ω, 使E (ψ) ∈Ω;然后, 构造目标泛函; 再求解变分问题:

当J取到极小J*时, E* (ψ) 就是我们所要得到的误差算子。这里最好用到全部历史资料, 原则上无困难, 技术上是现成的, 但工作量特别大。

1.2 相似误差订正方法

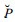
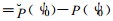
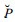
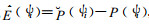
由于有了数值模式, 存在更简便的解法。对于当前的初值ψ0, 由式 (1) 可以得到预报量P (ψ0), 由准确模式可得实际观测 (ψ0)(未知的), 那么, Ê (ψ0)就是预报误差, 于是有P (ψ0)+Ê (ψ0), 问题归结为求取Ê (ψ0)。因此, 在改进动力模式的预报上, 我们可以换一种角度思维, 不正面攻坚, 改为对动力模式的预报误差进行预报。当然, 很容易想到的是, 如果对历史上大量实况做初值ψi (i=1, 2, …, n), 同理, 可由数值模式 (1) 得到预报量P (ψi), 由准确模式可得实际观测 (ψi) (已知的), 那么, 就是历史预报误差, 于是由算术平均可得

这就是我们熟悉的系统性预报误差。一个人想到用Ê对当前的预报进行订正P (ψ0)+Ê, 我们不会认为这个人特别聪明。此时, 虽然利用了历史资料信息来改进模式预报, 但这样做出的预报仍不具备针对性。

从数学上可以证明, 对线性系统资料用得越多越好, 对非线性系统则不然, 有巧不在多。由此, 针对各地特定的预报对象, 类似于相似预报的做法, 就可从历史资料中找出当前初值ψ0的相似状态。

如果找到一个历史相似ψ1, 有

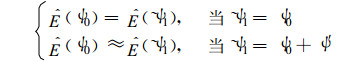
(5)

如果找到若干个历史相似ψj (j=1, 2, …, m), 比其他的更接近于ψ0, 则问题转化为

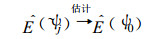
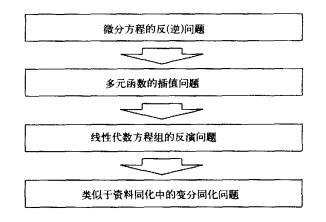
这表明, 当前预报中未知的误差项可以由历史上与当前初值相似的预报误差项估计来得到②[25]。在T63模式上的初步工作已经证明了其可行性和有效性[24], 并已被发展为一种相似误差订正法[25]。这种另类方法的好处在于无需构建新的模式, 只需利用历史相似数据运转现有的数值预报模式, 这不但克服了以往模式只用初值的缺陷, 而且, 通过对各地特定预报对象选取相似的过程实现了预报的针对性。进一步的理论分析①指出, 围绕如何利用历史相似预报误差估计当前模式预报误差的问题, 上述另类途径和方法可以遵循图 1中的步骤继续开展研究①[25]。

图 1. 开展另类途径和方法研究的步骤示意图

② 丑纪范.月平均环流的相似-动力模式.个人通信. 2003年4月25日.

2 另类途径的一个范例

在微分方程正问题产生不久就出现了微分方程的反问题。被恩格斯誉为是“科学上的一个勋业”的天外行星———海王星的发现便是解反问题的惊人成就。而其与前述订正模式预报误差的反问题有异曲同工之处 (参见图 2)。在19世纪中叶, 人们发现当时的数值模式所预测的天王星的位置与观测实况不符, 这是为什么呢？巴黎天文台台长Le Verrier (正是他最早组织了天气服务) 认为这是由于模式没有考虑到天王星轨道外的一颗新的未知行星的摄动作用所造成的。他在1846年8月31日提交给法国科学院的论文“论使天王星运行失常的行星, 它的质量、轨道和现在的位置的决定”, 成功地解决了这个问题。他依据天王星数值模式所做的预测的误差反推出了模式中未能考虑的作用 (海王星)。

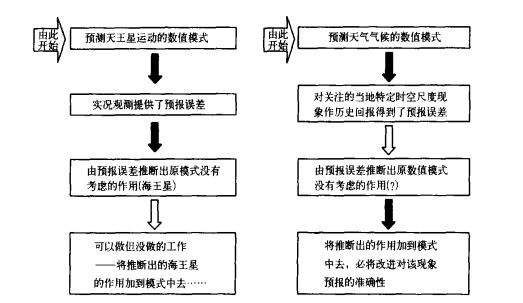
图 2. 发现海王星的反问题与订正模式预报误差反问题的对比 (实心箭头表示已做的, 空心箭头表示未做的)

当时, 他显然可以做但没有做的一个工作是将推断出的海王星的作用加到模式中去, 从而改进天王星的预测, 而这恰恰是我们的专业领域所最关注的问题。一百五十多年前Le Verrier能做成的事情, 在解反问题的理论、方法和技术都有极大发展的今天, 难道我们不能依据数值天气预报模式的预报误差, 推断出模式未能考虑的作用, 并将其作用加到模式中去, 从而改进预报么？我们提出的另类途径正是找到了一个在理想方案和省 (地、市) 气象部门目前能够实现的方案之间的平衡点, 是一个大有可为、各地应广泛开展的数值预报发展思路。但正如发现海王星所带给我们的启示, 解反问题找到数值模式中未能考虑的重要过程、并藉此提高模式对各地高影响天气的预报准确率, 才是不断追求的奋斗目标。

3 总结与讨论

当前的数值预报模式已不能满足各地日益增长的提高预报准确率的要求, 针对这一现状, 广大省 (地、市) 气象部门开展数值预报是很有必要的, 但不宜重复主流途径的做法, 应开辟适合于各地特定情况的另类途径。本文正是从理论上阐述了这种另类途径的内容、方法和意义, 强调其好处是无需构建新的模式 (对于地方上的研发力量, 这也是非常困难的工作), 只需利用所关心现象的历史相似数据运转现有的数值预报模式, 订正当前预报结果, 使之本地化, 因而是完全可行的。这不但克服了以往模式只用初值的缺陷, 而且, 通过对各地特定预报对象选取相似的过程实现了数值模式预报的针对性。

需要指出的一点是, 如果你认为外国没有的, 我们不要做, 那你千万不要搞这个另类途径。这是一片待开发的处女地, 在等待着有精力、有志于自主创新的人。

参考文献
[1] Bjerknes V. Das problem der wettervorhersage, betrachtet vom stadpunkte der mechanik und der physik. Meteor Zeit, 1904, 21: 1–7.
[2] Charney J G, Fjortoft R, von Neumann J. Numerical integration of the barotropic vorticity equation. Tellus, 1950, 2: 237–254.
[3] 丑纪范, 徐明. 短期气候数值预测的进展和前景. 科学通报, 2001, 46, (11): 890–895.
[4] 丑纪范. 为什么要动力-统计相结合?———兼论如何结合. 高原气象, 1986, 5, (4): 367–372.
[5] 顾震潮. 作为初值问题的天气形势预报与由地面天气历史演变作预报的等值性. 气象学报, 1958, 29, (2): 93–98.
[6] 顾震潮. 天气数值预报中过去资料的使用问题. 气象学报, 1958, 29, (3): 176–184.
[7] 丑纪范. 天气数值预报中使用过去资料的问题. 中国科学, 1974, 17, (6): 814–825.
[8] 郑庆林, 杜行远. 使用多时刻观测资料的数值天气预报新模式. 中国科学, 1973, (2): 289–297.
[9] 丑纪范. 长期数值天气预报的若干问题∥中长期水文气象预报文集. 北京: 水利电力出版社, 1979: 216-221.
[10] 邱崇践, 丑纪范. 改进数值天气预报的一个新途径. 中国科学 (B辑), 1987, (8): 903–910.
[11] 邱崇践, 丑纪范. 预报模式识别的扰动方法. 大气科学, 1988, 12, (3): 225–232.
[12] 邱崇践, 丑纪范. 预报模式的参数优化方法. 中国科学 (B辑), 1990, (2): 218–224.
[13] 邱崇践, 丑纪范. 天气预报的相似-动力方法. 大气科学, 1989, 57, (2): 131–142.
[14] 黄建平, 王绍武. 相似-动力模式的季节预报试验. 中国科学 (B辑), 1991, 21, (2): 216–224.
[15] Huang J P, Yi Y H, Wang S W, et al. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Quart J Roy Meteor Soc, 1993, 119: 547–565. DOI:10.1002/(ISSN)1477-870X
[16] 曹鸿兴. 大气运动的自忆性方程. 中国科学 (B辑), 1993, 23, (1): 104–112.
[17] 张培群, 丑纪范. 改进月延伸预报的一种方法. 高原气象, 1997, 16, (4): 376–388.
[18] 谷湘潜. 一个基于大气自忆原理的谱模式. 科学通报, 1998, 43, (1): 1–9.
[19] 龚建东, 李维京, 丑纪范. 集合预报最优初值形成的四维变分同化方法. 科学通报, 1999, 44, (10): 1113–1116.
[20] 曹鸿兴, 谷湘潜. 自忆谱模式制作中期天气预报的试验. 应用气象学报, 2000, 11, (4): 455–466.
[21] 魏凤英, 封国林, 曹鸿兴. 区域气候自忆模式中记忆系数的某些特征及汛期降水预报分析. 应用气象学报, 2000, 11, (4): 467–473.
[22] 封国林, 曹鸿兴, 谷湘潜, 等. 一种提高数值模式时间差分计算精度的新格式———回溯时间积分格式. 应用气象学报, 2002, 13, (2): 207–217.
[23] 陈伯民, 纪立人, 杨培才, 等. 改善月动力延伸预报水平的一种新途径. 科学通报, 2003, 48, (5): 513–520.
[24] 鲍名, 倪允琪, 丑纪范. 相似-动力模式的月平均环流预报试验. 科学通报, 2004, 49, (11): 1112–1115.
[25] 任宏利, 丑纪范. 统计-动力相结合的相似误差订正法. 气象学报, 2005, 63, (6): 988–993.