应用气象学报  2006, 17 (2): 232-239   PDF    
引用本文
吴翠红, 万玉发, 吴涛, 金鸿祥. 雷达回波垂直廓线及其生成方法[J]. 应用气象学报, 2006, 17(2): 232-239.
Wu Cuihong, Wan Yufa, Wu Tao, Jin Hongxiang. Vertical Profile of Radar Echo and Its Deteermination Methods[J]. Journal of Applied Meteorological Science, 2006, 17(2): 232-239  
雷达回波垂直廓线及其生成方法
吴翠红1,2, 万玉发3, 吴涛4, 金鸿祥2     
1. 南京大学大气科学系, 南京 210093;
2. 武汉中心气象台, 武汉 430074;
3. 中国气象局武汉暴雨研究所, 武汉 430074;
4. 湖北省十堰市气象局, 十堰 442000
2005-05-16 收到, 2005-11-04 收到修改稿.
资助项目: 湖北省科技攻关计划课题 (2004AA306B01)、湖北省国际科技合作课题 (2005CA012) 及湖北省气象局科技发展基金项目 (2003ZZ01) 共同资助    
摘要: 研究雷达回波Z (R) 垂直廓线VPR有两个重要内容: 一是VPR的生成方法, 二是用VPR订正雷达估算降水的技术。在简要比较现有生成方法———参数法、平均法和识别法的主要特点后, 认为平均垂直廓线MVPR具有简便、实用的优点。文章着重对MVPR的生成方法作了细致的探讨, 形成了4种生成算法, 并作了比较; 展示了各种生成参数对MVPR的不同作用, 并简要介绍了一个应用程序框图。对两个降水实例实施订正后初步评估表明, 用MVPR订正雷达估算降水可使评估因子R/G从0.84 (0.86) 提高到0.93 (0.97), 而绝对误差率则下降4%。
关键词: 雷达回波垂直廓线    VPR生成方法    降水订正    
Vertical Profile of Radar Echo and Its Deteermination Methods
Wu Cuihong1,2, Wan Yufa3, Wu Tao4, Jin Hongxiang2     
1. Department of Atmospheric Science, Nanjing University, Nanjing 210093;
2. Wuhan Central Weather Office, Wuhan 430074;
3. Institute of Heavy Rain, China Meteorological Administration, Wuhan 430074;
4. Shiyan Meteorological Bureau, Hubei Province, Shiyan 442000
Abstract: Radar beam's lifting and widening in the distance and the vertical nonuniformity of the natural distribution of water content in the atmosphere are important factors of radar detecting rainfall errors. During 1980s—1990s, the importance of vertical profile of reflectivity (VPR) to radar detecting rainfall is emphasized and the study on the VPR technology is conducted. There are two major aspects on the researches of VPR, one is the determination method of VPR, the other is the technique to correct radar precipitation estimation. After comparing the major features of three existing determination methods, i.e., parameterization, averaging and identification, it is found that the mean vertical profile of reflectivity (MVPR) has the advantage of simplicity and utility. Four algorithms of MVPR are obtained and compared with emphasis on investigating the determination method for mean vertical profile (MVPR); and the different functions of determining parameters, especially for MVPR, are demonstrated. Results show that the R/G ratio can be enhanced from 0.84 (0.86) to 0.93 (0.97) and the AD of radar rainfall estimation can decrease by 4% after the MVPR correction in the two precipitation cases. Among the four algorithms of MVPR, M11 is the best one in which the ratio profile takes the near groundlevel as the datum plane so that the feasibility of radar precipitation correction can be assured, and it has better representation owing to consideration of the same weighing of each bin in domain D. The MVPR algorithms relate to 8 attribute parameters, of which some values exert significant effect on the quality of MVPR. For example, the initial distance Ds in domain D obviously affects the profile shape below 1 km, therefore 1~5 km should be adopted; the distance outside D0 domain D plays its role from near ground-level to 6 km and the smaller D0, the smaller the more smoothing due to the beam widening, so 40~50 km should be adopted; the smaller the value of the vertical piecewise-height Δh, the more detailed the profile shape, so 250 m should be adopted. The evidence also indicates that when the exponent b in the different Z-R relationships are kept constant, the slope of the profile below 1.5 km will increases and the bright band of the profile will be more distinguishable with the decrease of the coefficient A. By analyzing VPR derived from the volume data in terms of VCP21 model of CINRAD/SA in Wuhan, it is found that the bright band locates at the height of 5 km and the radar precipitation estimation is generally not affected by the bright band when using 0.5° reflectivity PPI (or hybrid scan) within radius of 200 km. When echoes of major precipitation system in domain D, Z (R) below the bright band decreases with the height (dZ/ dh < 0), and these may be the causes why radars underestimate summer rainfall (especially for long distance) in the middle reaches of the Yangtze and it could be done by means of VPR to correct the radar precipitation estimation.
Key words: radar echo vertical profile     VPR determination method     precipitation correction    
引言

自从20世纪中叶气象雷达问世以来, 雷达定量测量降水一直是一个重要的研究领域。在经历了重点研究Z-R关系和用雨量计调整阶段后, 至20世纪80至90年代, 以Joss等[1]为代表的学者们, 开始强调雷达回波垂直廓线VPR (Vertical Profile of Reflectivity) 对雷达测雨的重要性, 充分认识到雷达波束采样随距离的抬升和展宽, 以及大气中降水强度在垂直方向自然分布的不均匀性, 正是雷达测雨产生误差的重要因素之一。20世纪90年代以来, 又取得了许多研究成果[2-11]。

Vignal等[7]曾明确指出, 有关VPR的研究有两个主要内容, 一是雷达回波垂直廓线的生成方法, 二是用VPR订正雷达估算降水的技术。本文重点就VPR生成方法的研究作出总结, 而有关降水订正应用举出两个试验实例。在VPR研究的15年中, 主要出现了3类生成VPR的方法, 即参数法[4]、平均法[3]和识别法[5-7]。若从实用效果来衡量, 目前当推平均法为首。本文重点研究平均垂直廓线MVPR (Mean Vertical Profile of Reflectivity) 的生成方法, 提出了生成MVPR的4种算法, 对生成垂直廓线的各种参数及其作用作了讨论和比较, 展示了参数选择对廓线生成的重要性。最后给出了一个平均廓线生成应用软件的程序结构框图及两个试验实例。

1 雷达回波垂直廓线3种生成方法及其重要特点

雷达回波在本文中特指天气雷达测量的反射率因子 (单位: mm6/m3), 或据Z-R关系式转换的降水率R (单位: mm/h), 因此雷达回波的垂直廓线可统称为Z (R) 垂直廓线。在VPR研究和应用中, 主要有下列3种生成VPR的方法。

1.1 参数法

参数法又称分析法, Koistinen[2], 特别是英国的Kitchen等[4]和Smyth等[6]相当注重此法, 并应用于英国的业务中。参数法试图用一条理想化的点廓线模拟实际大气的局地廓线。其方法要点为用高分辨率 (0.28°) 的Chilbolton的S波段雷达获得的大量RHI资料, 在层状云降水条件下, 归纳出典型的VPR模型, 然后根据每个像元 (5 km×5 km) 的雷达实测、地面气温和红外云图数据, 实时决定VPR的一些局地特征并实施地面降水订正。

1.2 平均法

平均法即为用平均算法 (见第2章) 求取雷达垂直廓线的方法, 简称MVPR。它是在一个特定区域D内, 对雷达实测的反射率因子值分层求取平均值后得到的。所以它可以当作D域内的代表性廓线 (representative profile), 当然代表性的好坏取决于地理、季节和天气条件。为了保证廓线在整个雷达有效探测范围内具有较好降水订正作用, 生成廓线的D域必须遵循一定的条件 (见3.3节)。MVPR的计算相对简单, 实用性很强, 并且用它订正雷达估算地面降水的效果也比较好, 几乎与识别法接近。平均法在瑞士由Joss开创, 已在20世纪中期开始用于业务, MVPR还常为其他廓线生成如识别廓线 (见1.3节) 提供原始廓线。

1.3 识别法

识别法由法国的Andrieu首创[5], 经Vignal等[7]加以扩充推广。通过雷达实测得到MVPR后, 用Menky反算理论的逆算法, 求出一个消除了雷达波束平滑作用的所谓真实廓线 (true profile), 特称为识别廓线 (identified profile)。而将雷达实测得到的MVPR称为表面廓线 (apparent profile); 但是它也是在特定D域内的一条代表性廓线。Vignal等[9]还将D域划分成144个小区域, 分别求取识别廓线, 特称为LVPR (local VPR)。经过二次与MVPR比较试验, 用识别廓线订正雷达估算降水的正确率只提高了2%~3%[8-9], Berne等人认为这只得到边缘性的改进[12]。但它计算工作量十分庞大, 成为业务应用的障碍[9]。几乎与Vignal同时, 美国的Seo等[10]亦提出了一个类似于识别法的距离订正算法RCA (Range Correction Algorithm), 但它没有和MVPR方法作比较。由史锐等[13]提出的拟合法, 它是据某些雨量站上空的实测VPR, 利用最小二乘法曲线拟合算法, 外推估算地面Z值, 其廓线基本属于表面廓线。

2 平均垂直廓线的生成方法

一般而言, VPR或MVPR均可泛指雷达反射率因子Z或经转换的降水强度R的垂直廓线, 为方便起见, 本文将Z转换成R进行计算; 同时应用武汉CINRAD/SA雷达三维极坐标高分辨率基数据, 以保证应有的精度。Joss等[3]当时因受最大回波强度图产品的限制, 只能采用直角坐标; 由于计算VPR最好应用雷达三维极坐标的基数据, 所以以下的方法和算法表达均基于三维极坐标系统。

2.1 MVPR的相关定义

为了清晰地表达有关MVPR的系列算法, 下面就几个基本概念进行简要表述和定义。

① 垂直廓线VPR: D域上某点u (r, α) 雷达回波强度R随高度h的分布, 以R (u, h) 表示。r为距离, α为仰角。

② VPR的比值廓线和订正廓线: 比值廓线是D域上某点雷达回波强度R (u, h) 与地面强度R (u, 0) 的比值随高度h的分布, 用P (u, h) 表示; 订正廓线则是比值廓线的倒数, 用Fa (u, h) 表示。二者定义为:

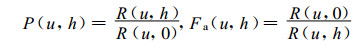
(1)

实际上可以认为比值廓线是以地面R (u, 0) 为基准经规格化了的垂直廓线。

③ MVPR及其比值廓线: MVPR是指在给定的D域内雷达回波强度平均值随高度的分布, 也可认为是众多VPR在D域内的平均, 用RD (h) 表示; 而MVPR的比值廓线则是众多P (u, h) 在D域内的平均, 用PD (h) 表示。二者定义为:

(2)

式 (2) 中, AVE表示平均运算。

2.2 MVPR的平均算法 2.2.1 比值廓线的两个算法公式

MVPR的比值廓线PD (h) 可用MVPR1和MVPR2两种算法获得。

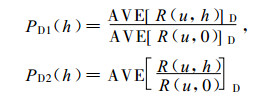
(3)

因商的数学期望不等于分子和分母各自数学期望的商, 以上二式表示的PD (h) 会有一定程度的不同。

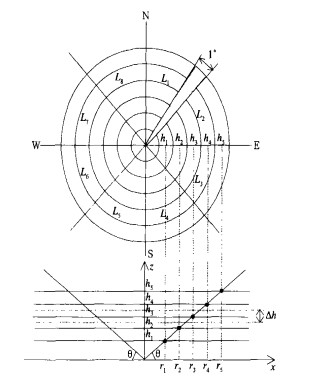
2.2.2 两个平均运算步骤

由式 (3) 可见, PD (h) 是基于MVPR的RD (h) 求取的, 而RD (h) 的平均算法又可有二种运算步骤, 现在以MVPR1的定义来叙述RD (h) 在三维极坐标中的具体算法, MVPR2则类似。对一个仰角为θ的PPI划分高度层如图 1所示, 层间厚度Δh任选。方位夹角为1°, 对应Δh厚度的径向增量为Δr的单元称为bΔh, 显然它与沿着雷达径向夹角为1°范围的1 km增量b不一定相等, 而与θ, h有关。

图 1. 仰角θ的PPI分层示意图

① 一次平均运算步骤S1。以b而不是以bΔh为本算法的计算单位, S1将平均运算从距离-方位-仰角一次完成, 如下式:

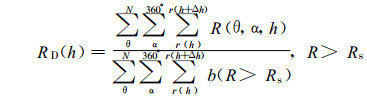
(4)

式 (4) 中, R为降水强度 (单位: mm/h), α为方位角, 可取360°或某一扇形夹角 (图 1), θ为仰角, r (h) 和r (h+Δh) 为距离, N为仰角数, Rs为指定降水强度阈值。式中分母为R > Rs时b的总个数。

② 三次平均运算步骤S3。bΔh中的平均降水强度R值是本算法的计算单元, 表示为[Rb (θ, α, h)]bΔh。S3将距离平均、方位平均和仰角平均 (等高层内) 3个平均运算步骤分开进行, 依次迭代后得到S3下的MVPR表示式:

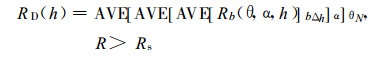
(5)

其中θN为等高层内仰角数。

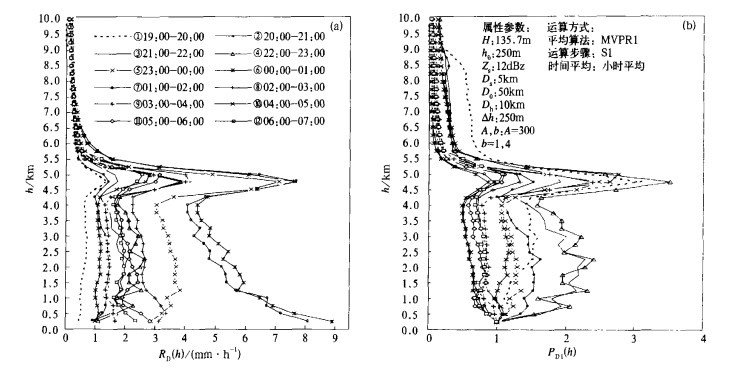
2.2.3 生成MVPR的4种平均算法及其比较

现将式 (3) 和式 (4)、式 (5) 相结合, 可得到生成MVPR的4种平均算法:并标记为M11, M13, M21, M23, 数值分别表示算法和步骤序号, 如M11表示为MVPR1和S1的结合算法。有了这些算法, 就可方便地生成某一D域和时段的平均雷达回波强度R的垂直廓线和比值廓线, 图 2为M11算法得到的2004年6月18日降水过程连续12个时次的平均廓线及其对应的比值廓线。虽然由同一次体扫通过这4种平均算法得到4个不同的MVPR, 它们有时近似有时有一定差别, 取决于Z (R) 空间分布的统计特征。但经过初步试验比较, M11的算法为最佳, 依次为M13, M21和M23, 所以本文后面用于雷达估算降水的订正廓线是基于M11算法而得到。

图 2. 武汉雷达 (下同) 2004年6月17日19:04 (世界时, 下同) —18日07:00 12个时次的平均垂直廓线 (a) 及其比值廓线 (b)

① PD1 (h) 与PD2 (h) 的比较。从算法上看, 当离雷达20 km以远随着0.5°仰角轴线的抬高, 使得PD2 (h) 算式中的分母R (u, 0) 不可能得到近地层 (本文定为0.25 km) 的值, 形成的比值廓线就不是严格以近地面为基准, 无法进行雷达估算地面降水的有效订正; 另外, 该算法是先求比值后平均, 显然平均比值廓线的垂直分布会对D域内不同雨强面积的大小较为敏感, 从而影响到垂直 (比值) 廓线的稳定性。MVPR2的具体算法程序也相对复杂些, 故现有大部分工作如Joss等[3]和Seo等[10]用的都是MVPR1。

② S1和S3的比较。S1运算步骤式 (4) 表示在D域内某一等高层中各仰角波束所包含的每一个b单元以等权重参加平均, 而S3运算步骤式 (5) 是以bΔh单元参加平均。对于近地面高度而言, 低仰角中一个bΔh可包含多个b, 如0.5°仰角在0.25 km高度内一个bΔh可包含20多个b, 并分布于较长的距离范围; 而高仰角中一个bΔh包含较少的b, 有时甚至只有一个b, 主要分布于近距离。因此, 由S3算法得到的廓线底部主要受制于近距离的回波强度, 而S1算法只能够反映整个D域范围的平均状况。

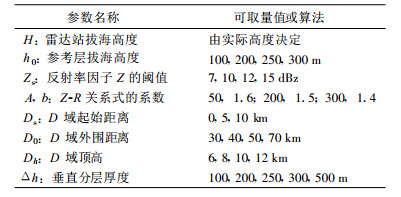
3 MVPR的生成参数和运算方式 3.1 生成参数和运算方式

在生成MVPR时, 有8个属性参数 (表 1) 以及有5种运算方式 (表 2), 可在生成通用软件 (见3.4节) 时选择或修改。

表 1 MVPR的生成属性参数

表 2 MVPR的运算方式

3.2 生成参数和运算方式的作用

如何合适地选取生成参数和运算方式, 对生成MVPR的质量, 有时会起到很大作用, 举例如下:

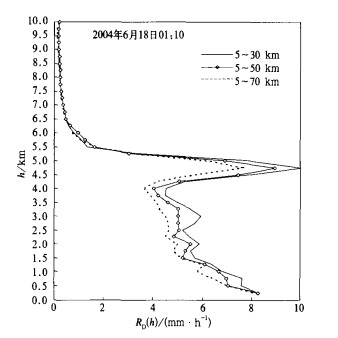
① D域参数Ds和D0的选取。不同的Ds会对1 km以下的廓线形状产生明显影响, 相应对订正雷达估算降水会产生不同的作用, Ds需根据雷达站附近地形、建筑物以及相应的回波质量来确定; 而外围距离D0的作用显然表现在近地层以上至6 km (图 3), D0越小波束展宽平滑作用越小, 越接近真实廓线, 而越大则相反, 应以40~50 km为宜。

图 3. D域不同外围距离D0的平均廓线

② Δh参数的选取。由分层厚度Δh决定的MVPR (图略), 除500 m以外其余基本相同, 但以100 m分层的廓线形状细节表现充分, 但对订正地面降水作用影响不大且计算量增多, 故应以250~300 m为宜。

③ Z-R关系式A, b系数选取。由图 4可见, 将常用的 (200, 1.5) 和 (300, 1.4) 相比较, 廓线形状差别不大, 但与我们最近研究的 (50, 1.6) 比较则有很大差别。用 (50, 1.6) 时, 在1.5 km以下廓线的斜率加大, 廓线亮带表现更突出, 这是不是更接近真实呢？值得重视。

图 4. 不同Z-R关系的平均垂直廓线

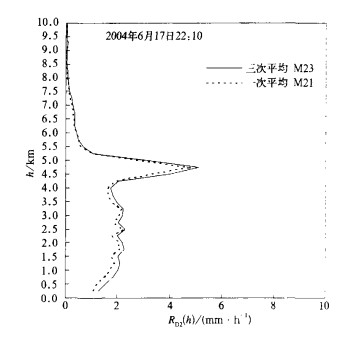
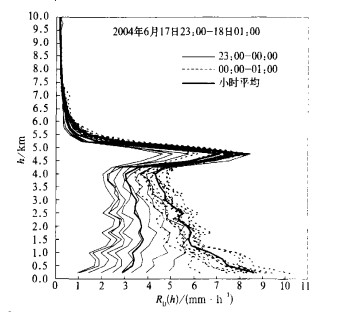
④ 二种平均算法和运算步骤的作用。由图 5可见, S1, S3在亮带层以下的量值有不小差别; 而从图 6可见, M21和M23在亮带层几无多大差别, 这表明在同次探测条件下, 用不同平均算法及步骤会得到不同的结果。图 7展示了在D域内8个小区域的平均廓线, 表现出不同的分布特征。图 8则演示了两个小时内的逐次体扫平均和小时平均廓线的丰富特征。由上可见参数及运算方式合理选择的重要性。各类选择的最佳组合, 将有助于生成一个有利于降水订正的MVPR, 这应与雷达站的地理环境及天气和降水类型密切有关。

图 5. 一次和三次运算步骤的平均垂直廓线

图 6. 一次和三次运算步骤的比值廓线

图 7. D域中8个扇形区域的局地垂直廓线 (L1~L8) 廓线

图 8. 2个小时逐次体扫平均垂直廓线及小时平均

3.3 MVPR生成域D的必要条件

综上所述, 要获得一个高质量且具代表性的MVPR, 生成域D必须具备如下条件:

① D域应以雷达站为中心, 半径限于50 km左右范围内。因为在这个范围内, 一是水平和垂直分辨率较高, 可以获得较为理想的Z (R) 样本值; 二是0.5°仰角轴线的抬升大都不超过0.5 km, 所产生的廓线可以下延及近地面, 符合订正地面降水的需要 (图 3)。

② 在D域内应有良好的雷达能见度[3], 即雷达四周最好是地形平坦无阻挡, 这样才能客观反映雷达回波的真实分布。

③ MVPR的主要作用是对D域外的雷达回波强度进行垂直订正, 由此D域尤其是雷达近距离范围, 必须分布有 (最好充满) 能够代表整个雷达探测范围主要降水系统性质的回波, 这是一个十分重要的条件, 是保证降水订正效果的关键。从图 2和图 8廓线演变就能够清晰反映出D域内回波合理分布的重要性。

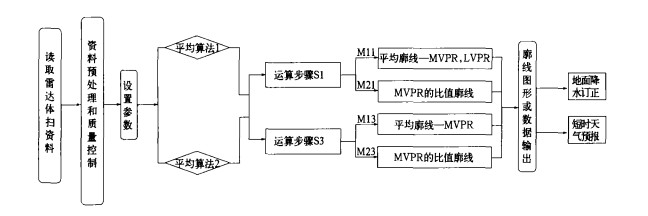
3.4 一个实用的MVPR生成程序的结构设计

此应用软件在CINRAD每次体扫后, 实时自动快速运行, 其输出结果立即进入下一步, 对雷达估算地面降水实施订正 (图 9)。

图 9. MVPR生成的软件设计框图

4 用MVPR订正雷达估算地面降水的初步试验

本文在重点研究MVPR生成技术的基础上, 选取武汉雷达探测到的两个降水过程进行订正试验, 以初步检验MVPR在雷达估算降水中的作用。

4.1 资料及MVPR生成参数

武汉CINRAD/SA雷达6 min频度的三维基数据 (VCP21扫描模式得到) 和相应雷达半径230 km范围的41个常规雨量站逐时雨量, 降水过程选取2004年6月17日20:00—18日07:00和2004年7月18日00:00—19日00:00, 共构成36 h的360个雷达体扫数据及1476个小时站次雨量数据。这里用来订正的MVPR是由M11算法得到, 其D域范围是距雷达1~50 km的环形区域, 垂直高度为10 km, 等高层间隔为0.25 km, 雷达反射率因子Z的域值为大于15 dBz。

4.2 订正评估方法

本文雷达探测的降水强度是基于0.5°PPI基数据估算的, 其中Z-R关系中的A=95, b=1.5。用每小时的MVPR对雷达半径230 km的估算降水强度作实时订正, 利用累积算法所得到的在覆盖区域内每像元 (1 km×1 km) 每小时雷达估算降水累积量分布图, 并求取整个降水过程的区域累积量 (图略)。评估样本用雷达逐时站点估算雨量Ri和雨量计逐时雨量Gi, 并用9个像元矩阵的best-match方法[14]进行配对, 以评估因子R/G和绝对误差率AD, 作为雷达降水估算和订正效果的判据。

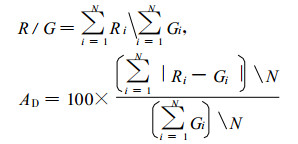
(6)

其中, N表示Ri和Gi同时不为零时的样本总数。

4.3 初步结果

① 2004年6月17日20:00—18日07:00降水过程

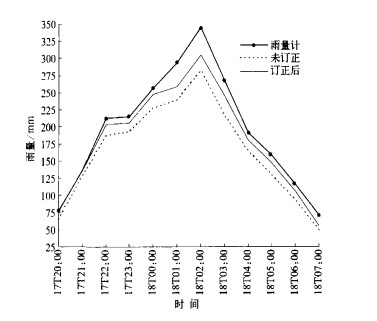
这是一次低层冷锋入侵造成的降水过程, 图 10表示了在雷达覆盖范围内雨量计Gi和雷达估算Ri逐时区域累积量演变。经过MVPR订正后, 评估因子R/G值由0.84提高到0.93, 绝对误差率AD值由22%下降到18%。

图 10. 2004年6月17—18日过程雷达估算地面降水逐时区域累积量订正前后的比较

② 2004年7月18日08:00—19日08:00降水

这是一次切变线的降水过程, 其中包含了多次小过程, 降水的对流性质明显增加。经过MVPR订正后, 评估因子R/G值由0.86提高到0.97, 绝对误差率AD值由25%下降到21%。

在试验中发现, 夏季长江中游地区的亮带层在近5 km高度处 (见图 2), 在雷达探测半径约200 km区域内对0.5°的探测基本不造成影响, 因此, 本文采用0.5°PPI强度场估算降水是合适的; 另外一个重要特点是, 当D域分布有主要降水系统性质的回波时, MVPR在亮带层以下Z (R) 表现为随高度下降 (dZ/dh < 0), 参见图 2~4, 这也许是我国夏季长江中游地区雷达探测降水远距离处常发生低估以及需要VPR订正的一个重要原因。

5 结语

20世纪90年代以来, 用VPR订正雷达估算降水技术的重要性已得到公认, 在订正因距离 (地曲、波束展宽)、地形阻挡 (波束抬高) 以及亮带等影响是有显著成效的。在VPR订正技术中, 首要需要解决的是VPR的生成方法, 即如何在一个雷达站方便快捷地生成一个VPR, 显然是最为重要的事。从本文分析3个现有的VPR生成方法看, 由平均法生成的表面代表性廓线即MVPR具有显著的优势, 首先来自实测数据, 且计算简单易行和实用有效, 这应该是一切应用科学的重要原则。MVPR生成方法虽然较为简单但也并非一成不变, 它也是可以发展的, 本文对此开始做了一点初步工作。而本文的试验实例说明, 用VPR订正雷达估算地面降水的技术, 在我国长江流域夏季是可行的, 并具有一定的效果, 对进一步提高雷达定量测量降水有积极的意义。同时, 试验还发现了一个VPR特性, 即在夏季长江中游 (可能扩及南方广大地区), 不是亮带本身而是在其下存在的降水递减率 (dR/dh < 0) 造成了雷达探测降水 (尤其是远距离) 普遍低估, 这也说明VPR订正是必要的。

参考文献
[1] Joss J, Waldvogel A. Precipitation Measurement and Hydrology∥Atlas D. Radar in Meteorology: Battan Memorial and 40th Anniversary, 1990: 577-606.
[2] Koistinen J. Operational Correction of Radar Rainfall Errors due to the Vertical Reflectivity Profile. 25th Int Radar Meteor Conf, AMS, 1991: 91-94.
[3] Joss J, Lee R. The application of radar-gauge comparisons to operational precipitation profile corrections. J Appl Meteor, 1995, 34: 2612–2630. DOI:10.1175/1520-0450(1995)034<2612:TAORCT>2.0.CO;2
[4] Kitchen M, Brown R, Davies A G. Real-time correction of weather radar data for the effects of bright band, range and orographic growth in widespread precipitation. Q J R Meteorol Soc, 1994, 120: 1231–1254. DOI:10.1002/(ISSN)1477-870X
[5] Andrieu H, Creutin J D. Identification of vertical profiles of radar reflectivity for hydrological applications using an inverse method. Part1: Formulation. J Appl Meteor, 1995, 34: 225–239. DOI:10.1175/1520-0450(1995)034<0225:IOVPOR>2.0.CO;2
[6] Smyth T J, Illingworth A J. Radar estimates of rainfall rates at the ground in bright band and non-bright ban events. Q J R Meteorl Soc, 1998, 124: 2417–2434. DOI:10.1002/(ISSN)1477-870X
[7] Vignal B, Andrieu H, Creutin J D. Identification of vertical profiles of reflectivity from volume scan radar data. J Appl Meteor, 1999, 38: 1214–1228. DOI:10.1175/1520-0450(1999)038<1214:IOVPOR>2.0.CO;2
[8] Vignal B, Galli G, Joss J, et al. Three methods to determine profiles of reflectivity from volumetric radar data to correct precipitation estimates. J Appl Meteor, 2000, 39: 1715–1726. DOI:10.1175/1520-0450-39.10.1715
[9] Vignal B, Krajewski W. Large-Sample evaluation of two methods to correct range-dependent error for WSR-88D rainfall estimates. J Hydrometeor, 2001, 2: 490–504. DOI:10.1175/1525-7541(2001)002<0490:LSEOTM>2.0.CO;2
[10] Seo D J, Breidenbach J, Fulton R, et al. Real-time adjustment of range-dependent biases in WSR-88D rainfall estimates due to nonuniform vertical profile of reflectivity. J Hydrometeor, 2000, 1: 222–240. DOI:10.1175/1525-7541(2000)001<0222:RTAORD>2.0.CO;2
[11] Germann U, Joss J. Mesobeta profiles to extrapolate radar precipitation measurements above the Alps to the ground level. J Appl Meteor, 2002, 41: 542–557. DOI:10.1175/1520-0450(2002)041<0542:MPTERP>2.0.CO;2
[12] Berne A, Delrieu G, Andrieu H, et al. Influence of the vertical profile of reflectivity on radar-estimated rain rates at sgort time steps. J Hydrometeor, 2004, 5: 296–310. DOI:10.1175/1525-7541(2004)005<0296:IOTVPO>2.0.CO;2
[13] 史锐, 程明虎, 崔哲虎, 等. 用雷达反射率因子垂直廓线联合雨量计估测夏季区域强降水. 应用气象学报, 2005, 16, (6): 473–477.
[14] Klazura G, Kelly D S. A Comparision of High Resolution Rainfall Accumulation Estimation from the WSR-88D Precipitation Algorithm with Rain Gage Data. 27th Int Radar Meteor Conf, AMS, 1995: 31-34.