应用气象学报  2006, 17 (1): 94-99   PDF    
引用本文
冯汉中, 陈永义, 成永勤, 罗可生. 双流机场低能见度天气预报方法研究[J]. 应用气象学报, 2006, 17(1): 94-99.
Feng Hanzhong, Chen Yongyi, Cheng Yongqin, Luo Kesheng. A Study on the Forecast Method of the Low Visibility Weather of Shuangliu Airport[J]. Journal of Applied Meteorological Science, 2006, 17(1): 94-99  
双流机场低能见度天气预报方法研究
冯汉中1,2, 陈永义3, 成永勤4, 罗可生2     
1. 云南大学资环学院, 昆明 650000;
2. 四川省气象台, 成都 610071;
3. 中国气象局培训中心, 北京 100081;
4. 成都双流机场空管中心, 成都 610000
2004-12-28 收到, 2005-04-13 收到修改稿.
资助项目: 国家自然科学基金项目 (60072006) 资助    
摘要: 在信息量较大, 而预报对象与预报因子的关系又不清楚的状况下, 智能机器学习方法是解决这类问题的较好手段。利用1997—2001年成都站的常规探空资料和双流机场的地面观测资料, 使用支持向量机 (Support Vector Machines, 简称SVM) 方法, 选取多种核函数进行双流机场低能见度天气的预报建模试验。测试结果表明:以径向基函数和拉普拉斯函数构造的SVM预报模型实验效果最好, Ts评分分别为0.287和0.292, 远高于双流机场低能见度天气出现的频率 (0.155)。试验结果还表明:以径向基函数构造的SVM预报模型空报较多, 漏报较少; 而以拉普拉斯函数构造的SVM预报模型空报较少, 漏报较多。因此, 如果强调模型对低能见度天气预报的准确性, 则应采用以拉普拉斯函数构造的预报模型, 如果强调对低能见度天气的预防性, 则应采用以径向基函数构造的预报模型。
关键词: 低能见度天气    支持向量机    预报方法    
A Study on the Forecast Method of the Low Visibility Weather of Shuangliu Airport
Feng Hanzhong1,2, Chen Yongyi3, Cheng Yongqin4, Luo Kesheng2     
1. Institute of Resource and Circumstances of Yunnan University, Kunming 650000;
2. Sichuan Provincial Meteorological Observatory, Chengdu 610072;
3. China Meteorological Administration Training Center, Beijing 100081;
4. Chengdu Shuangliu Airport Management Center, Chengdu 610000
Abstract: At Shuangliu International Airport the frequent, long-time low visibility often leads to the delay of scheduled flight and affects the safety of the planes. With the development of social economy and the air transport, the low visibility weather of Shuangliu Airport arouses great concern of the air control authority of the airport. Because a number of the factors can result in the low visibility weather, the factor mechanism is complex, and meanwhile the correlativity between the factors and the low visibility weather is insignificant, meteorologists are concerned most about how to forecast such weather as possible as they can. While there are huge amounts of information, the relation between the forecast object and the factors is unclear. Given this, intelligent machine learning technique is a good method to solve this sort of problems. In order to improve the forecast, Support Vector Machines (SVM), an intelligent machine learning technique that can solve the nonlinear problems is employed in the research to study the forecast method of the low visibility weather of the Shuangliu Airport. SVM method nonlinear is mapped by kernel function from lower dimensional space to higher. The higher nonlinear correlativity between the factors and the forecast object is indirectly expressed in implicit expression. Finally, the dependence of the factor and the object is depicted, and the model is set up by support vector. Hence, the model is not only related to the forecasting factor, but the kernel function as well. By using the data from Chengdu radiosound observatory and Shuangliu Airport surface observatory through 1997 to 2001, the forecast models of low visibility weather of Shuangliu Airport are built by mean SVM method with several kernel functions. Test results show the forecast model constructed with the radial base kernel function and the forecast model constructed with Laplace kernel function are better than the others, in which Threat Score are 0.287 and 0.292 separately, far above the frequency (0.155) of low visibility weather occurring at Shuangliu Airport. Test results also show, in the SVM model constructed with the radial base kernel function, the false alarm is higher and the omitted alarm is lower; in the SVM model constructed with Laplace kernel function, it is opposite. Therefore, if the accuracy of low visibility weather forecast is emphasized, the model constructed with Laplace kernel function should adopted; but if the precaution is emphasized, the model constructed in radial base function should be selected.
Key words: low visibility weather     Support Vector Machines     forecasting method    
引言

影响双流机场能见度的天气现象主要有雾、降水、霾、烟、浮尘等, 雾是其中最主要的因素。能见度与飞行的关系十分密切, 低能见度现象是引发飞行事故最常见的因素。《双流机场气候志》表明:地处四川盆地的双流机场各季均可出现低能见度天气, 其中以冬、秋季居多, 夏季最少, 且具有显著的日变化规律。低能见度天气集中出现在07:00—09:00 (北京时, 下同)。双流机场低能见度日较多, 且持续时间长, 常导致飞行航班延误。由于导致低能见度天气出现的因素较多, 影响系统复杂, 预报难度较大, 因而如何尽可能地预报出低能见度天气的出现, 是承担机场天气预报服务保障的预报工作者最为关注的问题。在此, 我们以目前最有理论保证且具有处理非线性问题能力的机器学习方法———支持向量机[1], 运用成都常规探空资料和双流机场的地面观测资料对低能见度天气加以研究, 以期对其预报有一定的指示意义。

本文是利用SVM方法对双流机场低能见度天气进行研究的结果介绍, 包含3部分内容:首先简单介绍SVM分类的基本原理, 然后介绍所使用的资料及建立SVM分类学习机的过程, 最后对所建立的SVM分类学习机推广能力进行检验的结果分析。

1 SVM分类方法基本原理简介

机器学习问题可概括的表述为[1]:给定训练样本 (x1, y1), (x2, y2), …, (xl, yl), 其中xi∈RN, 为N维向量, yi∈{-1, 1}或yi∈{1, 2, …, k}, 给出预报数据集:xl+1, xl+2, …, xm, 通过训练学习建立分类模式M(x), 使其不但对训练样本能够正确分类, 而且具有较强的推广能力。即可以由模式对于输入的预报数据xi得到正确的对应输出值yi。

对于训练样本集的线性二类划分问题, 就是寻求函数:

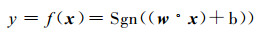
(1)

使对于i=1, 2, …, l满足条件:

(2)

其中w, x, xi∈RN, b∈R, w, b为待确定的参数, Sgn为符号函数。显然, (w·x)+b=0为划分超平面, w为法方向向量。

对于线性可分离的问题, 满足条件形如式 (1) 的线性决策函数是不唯一的。图 1给出二维情况下满足条件的划分直线的分布区域图。落在虚线区域内的任一直线都可作为决策函数。谁是最优的决策函数, 就要对其进行判断。

图 1. 划分直线的分布区域图 (图中◆表示有, ○表示无, 下同)

V.N.Vapnik提出一个间隔最大化原则①:寻求使间隔达到最大的划分为最优, 即是对w, b寻优, 求得最大间隔:max (min(‖x-xi‖:x∈RN, (w·x)+b=0, i=1, …, l)), 对应最大间隔的划分超平面称为最优划分超平面, 简称为最优超平面, 如图 2中的平面L。图 2中两条平行虚线l1, l2 (称为边界) 距离之半就是最大间隔。

图 2. 最优划分超平面示意图

① 陈永义. 支持向量机方法及其在气象中的应用. 中国气象局培训中心, 2004:61-64.

最大间隔和最优超平面只由落在边界上的样本点完全确定, 而不依赖于所有点, 称这样的样本点为支持向量, 如图 2中的x1, x2, x3样本点。

对于给定的训练样本集, 根据相关的理论和算法, 最终获得的线性支持向量机为:

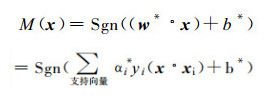
(3)

式 (3) 中Sgn ( ) 为符号函数; αi*, b*为确定最优划分超平面的参数; (x·xi) 为两个向量的点积。

对于线性不可分的情况, 通过非线性映射φ, 将样本集映射入一个高维的特征空间, 称为Hilbert空间, 使在样本空间中的高度非线性问题在高维空间中应用线性分类的方法得以实现。

由于在特征空间中采用的是线性分类方法, 所以在特征空间中的最优划分超平面分类函数的形式为:

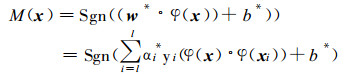
(4)

与式 (3) 相比, 式 (4) 只是用φ(x) 和φ(xi) 代替了x和xi。

根据Mercer定理[2], 式 (4) 最终转变为:

(5)

式 (5) 就是SVM方法确定的最终非线性分类的决策函数。与式 (3) 相比, 这里只是用Mercer核函数的计算代替了点积的计算, 在整个求解过程中不需要知道非线性映射的显式表达式。

2 建立低能见度天气的SVM分类学习机 2.1 资料

1997年5月—2001年12月成都双流机场本站的逐小时温度、露点、气压、相对湿度、能见度, 以及成都探空站逐日08:00, 20:00的位势高度、温度、露点、风向、风速。

2.2 预报对象

按照机场服务的需要, 以双流机场测站能见度小于800 m作为低能见度天气, 以此为预报对象, 进行低能见度天气的研究。

2.3 构建预报因子

低能见度天气主要由雾造成, 在四川盆地, 一般形成雾的大气主要特征有:近地面至925 hPa, 大气层结呈中性状态, 而925~500 hPa高度常有逆温层, 呈现出稳定状态; 从地面至400 hPa, 大气相对湿度较大, 接近准饱和状态, 近地层无风。因此, 为了尽可能地描述有可能形成低能见度天气的大气空间结构, 利用成都站每天08:00和20:00的400, 500, 700, 850, 925 hPa层次的位势高度、温度、露点、风向、风速等探空资料和双流机场00:00—21:00逐小时的温度、露点、气压、相对湿度等地面观测资料来构造样本空间, 每一个样本由138个变量构成。选取这些变量, 既保证了现有资料的充分使用, 也能反映各个要素随时间的动态变化过程, 进而构造一个比较完备的相空间。需要指出的是SVM是通过支持向量构造推理模型, 对因子的数量没有限制[3]。

2.4 构建样本序列

因使用的是常规观测资料, 故以经典统计预报方式建立样本序列, 即以t时刻的预报因子对应t+1时刻的预报对象。除去有问题的样本资料, 获得有效样本1108个。

2.5 建立SVM预报模型

从总样本中以随机抽样方式获取用于建立预报模型的训练样本936个, 剩余的172个样本作为测试模型优劣的实验样本。低能见度样本在训练样本中所占的比率为15.52%, 在实验样本中所占的比率为15.51%, 即低能见度样本在训练样本和实验样本中出现的几率一致。

虽然支持向量机方法具有较好的鲁棒性, 但是对于具体的应用问题来说, 选取不同的核, 或相同核函数下选取不同的参数都会对结果产生明显的影响[3], 而对于一个实际问题来说, 只能有一个推广能力最强的解。因此, 应用SVM方法解决实际问题时, 存在一个在这些不同条件下的最优解中选优的问题, 即使选不出最优, 也要找出可以实际应用的较优结果, 这就是SVM的参数选优问题。但至今在理论上还没有对此有好的解决方法。在建立预报模型时, 使用的是中国气象局培训中心推出的CMSVM软件。在建立具有推广能力的预报模型时, 要对核函数进行选取, 然后通过训练和测试确定核函数的参数, 进而确立具有较好推广能力的预报模型。研究中选取7种核函数 (满足Mercer定理) 进行相关的试验, 这7种核函数为:

① 多项式核函数:

② 径向基核函数 (RBF):

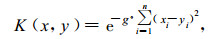
③ 对称三角形核函数:

④ 柯西核函数:

⑤ 拉普拉斯核函数:

⑥ 双曲正割核函数:

⑦ 平方正弦基数核函数:

试验结果显示出 (表 1), 以对称三角形核函数和柯西核函数分别建立的预报模型对训练样本的回报最好, Ts评分高达0.784, 但将对应的模型用于实验样本的预报结果 (表 2) 表明, 这两种核函数构造的预报模型漏报次数较多, 尽管假警报率较低, 但概括率较小, 实际使用的价值不大。

表 1 由不同函数构造的SVM分类学习机对训练样本进行回报的评价

表 2 由不同函数构造的SVM分类学习机对实验样本进行试报的评价

从表 2可以发现, 以径向基核函数和拉普拉斯核函数分别建立的预报模型, 尽管对训练样本的回报水平略差于前述的两种预报模型, 但其对实验样本的预报效果最好, Ts评分分别为0.287和0.292, 远高于低能见度天气在样本中出现的频率 (15.51%), 具有显著的正预报技巧。

从表 2还可以看出, 以径向基核函数构造的预报模型, 空报次数较多 (52次), 漏报次数较少 (25次); 而以拉普拉斯核函数构造的预报模型, 空报次数较少 (9次), 漏报次数较多 (37次)。因此, 如果强调模型对低能见度天气预报的准确性, 则应采用拉普拉斯核函数构造的预报模型, 如果要强调对低能见度天气的预防性, 则应采用径向基核函数构造的预报模型。

3 以径向基核函数为基础建立的SVM低能见度天气预测模型

研究低能见度天气的预测方法, 目的在于给出有警示性提示的预报结果, 提示相关的技术人员仔细分析资料, 最终对提示结果进行肯定或否认。依据前面的分析, 选取以径向基核函数为基础进行训练建立的SVM预测模型作为业务试用模型, 构成模型的核函数的参数值为g=0.07, c=420, 支持向量个数为601。表 3给出了构成预测模型的部分支持向量, αi为每一个支持向量对应的系数值, χi为构成支持向量的每一个预报因子 (对各因子值进行了归一化处理)。模型的最终预测结果, 由预测样本和支持向量通过式 (5) 计算得出, 若决策函数M(x) < 0, 则预测无雾; 若M(x)≥0, 则预测结果为有雾。

表 3 构成双流机场低能见度天气预测模型的部分支持向量

支持向量学习机方法是在看似杂乱无章的资料中寻求关键信息, 记忆关键样本, 通过对历史资料的学习, 积累知识, 类似于人脑的学习过程。对部分关键样本的本站气温、露点、气压、相对湿度进行分析后发现, 出现雾与否, 不在于温度的高低, 而在于相对湿度的大小, 温度高可以有雾发生, 温度低也可以产生雾, 关键看湿度的演变趋势。如图 3所示, 样本a, b, c为无雾的关键样本, 样本A, B, C, D为有雾的关键样本, 有雾出现之前, 00:00—21:00的相对湿度都较大, 且在15:00以后, 均呈现增加的趋势; 无雾出现之前, 10:00—16:00相对湿度较小, 或20:00—21:00相对湿度呈下降趋势。如果对支持向量的各要素进行仔细分析, 则可以认识形成雾与否的要素空间分布或随时间的演变趋势, 给出有无雾出现的基本特征, 为实际预报积累知识。如果对每一个个例进行分析, 就类似于经验总结。但由于雾的形成机理比较复杂, 且构成预报模型的支持向量较多, 逐一分析不太可能, 所以借助于机器学习方法也是解决问题的有效方式, 业务试验结果也表明:利用支持向量机方法建立的预测模型具有较好的稳定性和推广能力。

图 3. 作为支持向量的关键样本中相对湿度的逐小时演变情况 (虚线:无雾出现, 实线:有雾出现)

4 结语

目前, 对低能见度天气的预报仍以统计预报方法为主, 尽管随着数值预报的发展, 现在也有数值释用和雾模式预报, 但许多试验结果表明:雾模式仅有一定的机理分析用途, 难以实际预报, 而数值释用方法必须对模式因子做适当有效的处理, 否则难以有效, 因而除了经验预报以外, 统计法仍是目前较为实用的方法。严格说来, SVM方法也是一种统计预报方法, 只不过它是从样本资料中通过自学习的方式获取预报知识, 建立预报模型, 且SVM方法是通过核函数实现从低维到高维空间的非线性映射, 以隐式方式间接地表述预报对象与预报因子之间的高度非线性关系, 最终通过支持向量来刻化因子与对象之间的依赖关系。在预报因子与预报对象之间的关系并不明了之前, 基于机器学习的“黑箱”输出, 仍是目前比较实用的方法。

试验表明:双流机场低能见度天气的SVM分类预报模型, 对核函数的选取有较大的依赖关系, 如果强调对低能见度天气预报的准确性, 则应采用拉普拉斯核函数构造的SVM预报模型, 如果强调对低能见度天气的预防性, 则应采用径向基核函数构造的SVM预报模型。业务试验结果表明:利用支持向量机方法建立的预测模型具有较好的推广能力。

参考文献
[1] 陈永义, 俞小鼎, 高学浩, 等. 处理非线性分类和回归问题的一种新方法 (Ⅰ)———支持向量机方法简介. 应用气象学报, 2004, 15, (3): 345–354.
[2] Courant R, Hilbert D. Method of mathematical physics, Volume Ⅰ. Springer Verlag, 1953.
[3] 冯汉中, 陈永义. 处理非线性分类和回归问题的一种新方法 (Ⅱ)———支持向量机方法在天气预报中的应用. 应用气象学报, 2004, 15, (3): 355–364.