气象观测资料质量控制的重要性已经为所有使用气象资料的科学家所公认。地面气象观测记录必须具有代表性、准确性和比较性[1]。在“全球气候观测系统资料与信息管理计划”中特别提出, 为GCOS所建立的数据库系统中的数据必须经过严格的质量控制, 使数据质量符合标准, 以保证使用此类数据的研究人员能够接受[2]。
随着气候研究的深入, 各国都进一步加强了对气象资料的质量控制 (QC) 研究。近年来资料质量控制技术有了新的进展, 同时, 质量评估 (QA) 也已经发展和应用到各国资料部门中。在质量控制的同时, 对资料进行评估是必要的。尤其对进行质量控制的数据管理工作人员, 因为评估可以使其更好地决定是否使用某方法, 并且对检验出的结果有一个科学的认识。当然, 如果将评估结果提供给资料的使用者, 则可以使资料使用人员更好的利用资料。因此, 在国外, 近年来除了质量控制 (QC) 技术发展很快外, 质量评估 (QA) 也更加引起重视[3-7]。
传统的质量控制 (QC) 主要根据气象学、天气学、气候学原理, 以气象要素的时间、空间变化规律和各要素间相互联系的规律为线索, 分析气象资料是否合理。其方法包括:范围检查、极值检查、内部一致性检查、空间一致性检查、气象学公式检查、统计学检查、均一性检查[8]。这些方法被普遍应用到地面气象资料的质量控制中, 而且方法的综合应用有着很好的效果。随着自动站资料空间密度的增加, 尤其是高密度降水、气温、风资料的使用, 更需要对单要素的资料质量进行有效的控制。但是如果是单要素, 或者是新建的测站或测点 (如在我国大城市或乡镇密布的自动雨量站), 由于缺乏历史资料或要素之间的相互比较, 对其观测数据的质量控制就只有使用空间一致性检查比较合适。有许多进行空间插值估计的方法[9], 其取决于气象变量、地理环境、台站的空间分布等, 如:正态比例法、反距离权重法、内插法、单一最优估计、回归法等。对于空间检验, 我国资料检验部门还很少使用。因此, 本文介绍一种国外使用的“空间回归检验方法”[10], 并应用该方法对2003年地面观测的主要气象要素进行检验, 评估该方法在我国各地的适用性。期望对该方法的使用提供试验依据, 促进对单要素高密度资料检验技术的提高。
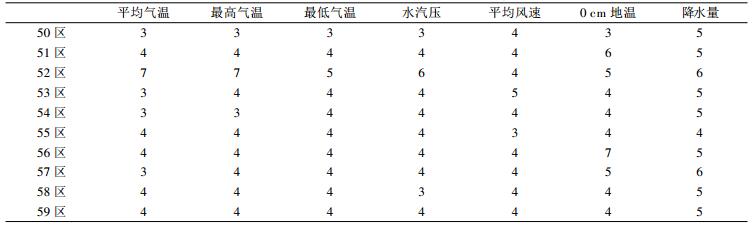
1 资料和方法 1.1 资料为了检验方法的适用性, 使用2003年我国671站的逐日平均气温、最高气温、最低气温、平均水汽压、平均风速、平均0 cm地温 (以下简称0 cm地温)、降水量。同时为了便于分析该方法在各地区的适用性, 按区号将全国台站划分为10个区。
50区包括45°N以北的黑龙江及内蒙古北部; 51区为35°N以北、92°E以西的新疆大部地区; 52区位于35°N以北、92°~105°E的地区, 主要包括内蒙古西部、甘肃、青海; 53区位于35°N以北、105°~115°E的地区, 主要包括陕西、山西、河北西部; 54区位于我国35°~45°N, 115°E以东地区, 主要包括辽宁、吉林、内蒙古东部、河北东部、京津、山东地区; 55区位于我国35°N以南、92°E以西的青藏高原地区; 56区位于35°N以南、92°~105°E地区, 包括青藏高原东部、四川西部、云南大部; 57区位于25°~35°N, 105°~115°E地区, 主要包括四川东部、河南南部、湖北、湖南、广西等地; 58区位于25°~35°N, 115°E以东地区, 主要包括安徽、江苏、江西、福建; 59区位于25°N以南、105°E以东地区, 主要包括广东、广西。
1.2 方法空间回归检验方法的主要思路是以参考站的观测值来判断被检验站的观测值是否在一定可接受的范围之内。首先选择距被检验站最近的一批站 (本次选择距被检验站正负两个经纬度范围)。在这一批站中, 以参考站和被检验站的一元回归方程的均方根误差为依据, 具有最小均方根误差的5个站为确定的参考站。给均方根误差小的参考站以大的权重来计算被检验站观测值的加权估计值和估计值的加权标准差。然后用加权估计值和估计值的加权标准差确定被检验站实测值的范围, 如果超出范围, 则认为数据可疑。
具体计算步骤如下:
① 相对于被检验站, 选择距被检验站最近的一批站。
② 每个站全月逐日数据作为一个序列, 逐对计算参考站与被检验站之间的相关系数, 并进行相关系数的显著性检验, 对于没有通过显著性检验的台站, 从参考站中剔除。
如果参考站少于5个, 则该被检验站不再做进一步的空间检查。
③ 逐对建立被检验站与各参考站的回归方程:
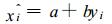
|
(1) |
式 (1) 中, 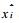
④确定5个参考站。求每对被检验站与参考站建立的回归方程的均方根误差:

|
(2) |
式 (2) 中, s为均方根误差, xi为被检验站某日的实测值, 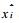
对每一对回归方程的均方根误差由小到大排序后, 找到前5个最小值。即确定有最小均方根误差的5个参考站。
⑤求加权估计值。计算被检验站的加权估计值x′:
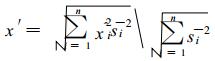
|
(3) |
式 (3) 中, 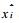
⑥求估计值的加权标准差s′:
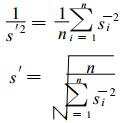
|
(4) |
⑦检验被检验站实测值, 如果超出范围, 认为数据可疑。

|
(5) |
式 (5) 中, f为质量控制参数, 简称质控参数。
对每个被检验值x重复⑤~⑦步, 逐值检查。
2 对空间回归检验方法的评估根据概率统计学[11], 我们知道, 当检验一个假设时, 总希望得到一个正确的判断, 但是实际上完全做到是不可能的。无论是接受还是拒绝一个假设, 所做的判断都有可能是错误的。其中有两种类型的错误, 其一类错误在数理统计中称为“第一类错误”即“把真当假”。在做质量控制的统计检验时, 如果数据正确而被拒绝, 则产生“第一类错误”。其二是“以假充真”, 即数据是错误的而被接受, 产生“第二类错误”。
在空间回归检验方法的使用中, 为了减少“第一类错误”, 可以采取扩大判别范围的方法, 在式 (5) 中扩大f值的数值, 但同时将增多“第二类错误”, 即扩大判别范围后, 增多了可能是错误数据被认为正确而接受。QA研究的必要性就是在减少“第二类错误”而不增加“第一类错误”之间找到平衡。一般情况是, 控制“第一类错误”的概率, 在此基础上选择使“第二类错误”达到最小的检验方法。在质量控制中, 如何选择判断的参数, 使数据经过检验后, 数据的质量达到一个适当的标准是重要的。
根据空间回归检验方法, 我们可以看到, 式 (5) 中, 如果被检验数据x在给定范围之内, 则数据通过检验; 从式 (5) 可以看出, 使用连续大的f值, 可以减少“第一类错误”。因此, 空间回归检验方法可以事先选择一个检测出的错误数据的比例, 其中的f值是一个变化的范围, 而不仅仅是单一的f值。应用该方法, 在选择统一出错率的基础上, 通过f值的变化, 使质量控制后的数据评估有一个可以接受的统一标准。因此, 可以在不同的气象站选择不同的f值, 这是该方法的第一个特点。
该方法的第二个特点是, 参考站不一定是与被检验站距离最近的站。参考台站的选取首先选距离近的站, 在此基础上再根据被检验站与参考站建立的回归方程的均方根误差为权重, 也就是使用了拟合最好的站来做为参考站, 用拟合最好的几个站来估计被检验站的数据。所以, 该方法的实质是:在被检验站邻近的一定空间范围内, 寻找与它相关性较好的站做为参考站。这是因为一元回归系数也就是相关系数, 相关系数高, 相关较好, 则方差也较小。虽然“空间回归检验方法”是一个考虑“空间”的检验方法, 但不象空间检验中的“反距离权重法”仅以距离做为权重估计被检验站的数据。因此, 空间回归检验方法比只考虑“距离”的“反距离权重法”有着更好的检验效果[12]。
3 检验结果及分析表 1列出了各区在不同f值下检验出的日平均气温平均出错率。应该说明的是: ①表 1中的平均值是由所有站检验出的认为是出错 (可疑) 的样本数除以全部被检验的样本数, 不是各区出错率的平均值; ②各区检验的样本数是有差别的, 由于计算时必须满足参考站数不低于5个, 在台站稀疏的区, 检验样本就少, 如55区的检验样本少。但是每个区出错率计算方法均为检验出的出错样本数除以检验样本数。
|
|
表 1 不同f值情况下, 各区日平均气温平均出错率 |
从表 1可以看出, 各区气温要素均是随着f值的扩大, 判为可疑数据的比率逐步减少, 同时, 各区减少的速度相差比较小。当f=3时, 平均气温全国平均出错率为0.07%; 除52区外, 各区均已经达到万分之几或更低的量级。当f=4时, 除56区和52区外, 出错率均为0.0。如果出错率选择在0.01%, 可选择f值在3~4之间。当f=9时, 52区出错率在0.1712%, 其余区没有检查出错, 经查, 52区的52645站 (青海省野牛沟) 6月全月数据判错。f=9是一个很大的容错范围, 数据仍然判为出错, 因此, 可肯定判定该站月数据有错。如去掉52645站, 经检验, 当f=7时, 52区出错率在为0.01%。因此, 一般地, 52区在出错率为0.01%时, 可选择f=7。
从以上计算结果可以看出, 当f值固定时, 各区的出错率相差比较大。当f=3时, 57区出错率达到十万分之几的量级、52区为千分之几的量级、其余区在万分之几的量级。因此, 检验气温时, 应该根据一般出错率经验, 在我国不同地区选择不同的f值, 使检验出的出错率控制在一定的比例内。也就是说, 如果固定出错率, 则不同地区应该选择不同的f值。
从表 2可以看出, 各区降水量也随着f值的扩大, 判为错误数据的比率逐渐减少。但是, 与气温要素不同, 各区减少的速度相差比较大。在检验降水中, 当f=3时, 平均出错率为5.42%, 这一比例高于一般的经验出错率, 因此, 不能取f=3。当f=5时, 平均出错率为0.04%, 除52区和54区外, 均在万分之一以下。这一比例符合一般的经验出错率。因此, 当使用该方法检验降水量时, 取f=5是合适的。当f=9时, 52区和54区仍错, 经查, 52576站6月25日和54471站2月25日数据判为有错, 因此判断这些数据有错。如果不检验54471站, 则当f=5时, 54区出错率为0。说明一般情况下, 54区选取f=5比较合适。
|
|
表 2 不同f值情况下, 各区降水量的平均出错率 |
降水量是空间变率比较大的要素, 空间检验的许多方法对降水要素的检验均不理想。而从以上试验及分析可以看出, 该方法对降水的检验有比较好的效果, 这也是该方法的一个优势。
从表 3可以看到, 当f=3, 平均出错率为0.06%; 当f=4, 平均出错率为0.0008%。因此, 在检验平均风速时, 可以取f=4。由于55区各站风速的相关差, 造成参加检验的站少, 表 3中55区参加检验的样本少, 出错比例下降比较快。由此也可以看出, 对于风速这一空间变率大的要素, 使用该方法检验, 也有比较好的效果。
|
|
表 3 不同f值情况下, 各区平均风速的平均出错率 |
同样, 应用空间回归检验方法检验了最高气温、最低气温、0 cm地温、水汽压 (表略)。结果表明:检验最高气温, 当f=3时, 平均出错率为0.0655%, 而当f=4时, 除52区有错外, 均未再检验出错。因此, f取3~4之间比较合适。经查, 52区是52645站6月资料有错。检验最低气温, 当f=3时, 平均出错率为0.05291%, 而当f=5时, 除52区有错外, 均未再检验出错。因此, f取3~4之间比较合适。经查, 52区也是52645站6月数据出错。检验0 cm地温, 当f=4时, 平均出错率为0.05980%, 而当f=5时, 平均出错率为0.01483%。因此, f取4~5之间比较合适。检验水汽压, 当f=3时, 平均出错率为0.05045%, 而当f=4时, 平均出错率为0.01045%。因此, f取3~4之间比较合适。
根据以上各要素的计算, 综合出各要素不同f值的全国平均出错率, 见表 4。
|
|
表 4 不同f值情况下, 各要素的平均出错率 |
从表 4可以看出, 当f=3时, 除降水量、0 cm地温外, 各要素的出错率在0.07%以下, 即万分之几的量级。当f=4时, 0 cm地温出错率为0.05%; 当f=5时, 降水量出错率达到0.04%。这一结果可以作为各要素全国范围内选择f值的参考。即当选择出错率为万分之几的量级时, 对降水量取f=5, 0 cm地温取f=4;其余要素取f=3。对于某一区, f取值可与全国平均取值不同。同样, 一个区的不同要素之间也有差别 (表 5)。从表 5可看出, 具体到50区, 选择出错率为0.01%时, 对降水量要素取f=5, 对平均风速f=4, 其余要素f=3。因此, 在检验各区的单要素资料时, 可以以表 5为例, 制作各区在固定出错率值后f的判断值。
|
|
表 5 不同f值情况下, 50区各要素的平均出错率 |
从以上分析可以看出, 当使用该方法进行质量检验时, 不同要素在不同地区检验的出错率不同, 为了在实际检验中应用该方法对不同要素的检验, 根据试验结果总结出表 6供参考。在实际检验中, 通常要求统一出错率标准, 表中选择了出错率为0.01%。
|
|
表 6 当出错率为0.01%时, 各区各要素的f值 |
从表 6中可以看出, 各地区各要素的f值有比较大的差别。当固定出错率时, 各区选择的f值不同。如气温选择0.01%的出错率, 50, 53, 54, 57区选择f=3; 52区选择f=7;而其余区选择f=4。在理论上, 出错率是在一定可信度的标准下被判断为错误的数据。在实际应用中, 是一种可疑数据。为了避免“以真当假”的情况, 还必须针对具体检验出的数据进行人工判断, 以确定是“可疑”还是“错误”。如果经过人工判断, “可疑”的数据是“正确”的结果比较多, 则应该调整f值, 以降低出错率。
从总体来看, 51, 52, 56区的各要素f值合计大于其他区, 这几个区的站点位于我国西部或西北部, 地处我国边境或青藏高原, 台站分布稀疏、地形复杂。55区比较特殊, 虽然也位于青藏高原, 但由于台站稀疏, 参加检验的样本数少, 通过检验的站结果比较好, 所以各要素f值合计值也不大。这说明, 与一般空间检验方法相同, 该方法也与地理环境、周边台站分布有关, 受到周边台站密度的影响。
4 小结1) 空间回归检验方法能够有效检验出可疑的数据, 适用于对单一要素的检验。尤其对降水、风速等空间变化比较大的要素, 该方法有比较好的检验效果。
2) 应用该方法计算时, 在不同的地区、不同要素之间存在差异。随着f值的扩大, 各区各要素判为错误数据的比率均逐渐减少。虽然如此, 各要素减少的幅度有比较大的差别。降水量要素各区减少的速度差别比较大; 其余要素减少的速度各区相差比较小。
3) 当固定出错率时, 各区应该选择不同的f值。与一般空间检验方法相同, 该方法也与地理环境、周边台站分布有关, 受到台站分布密度的影响。
| [1] | 中国气象局.地面气象观测规范.北京:气象出版社, 2003. |
| [2] | 全球气候观测系统中国委员会办公室.全球气候观测系统中国委员会成立大会暨委员会专家组第一次全体会议文集.北京:气象出版社, 1997:67. |
| [3] | WMO.Guidelines on Quality Control Procedures for Data from Automatic Weather Stations.CBS/OPAG-IOS/ETAWS-3/DOC.4(1), 2004. |
| [4] | Rudel E.Report and Review about Data Processing and Quality Control Procedures Involved in the Conversion of Manually Operated Station to Automatically Operated Station.World Climate Programme:zData and Monitoring No.31, WMO-TD No.833, 1997. |
| [5] | WMO.Automated Weather Stations for Applications in Agriculture and Water Resources Management:Current Use and Future Perspectives.Proceedings of an International Workshop.6-10 March 2000, Lincoln, Nebraska, USA, WMO/TD No.1074, 2001. |
| [6] | Mark Shafer A, Christopher Fiebrich A, Derek Arndt S. Quality assurance procedures in the oklahoma mesonetwork. J Atmos Ocean Technol, 2000, 17: 474–494. DOI:10.1175/1520-0426(2000)017<0474:QAPITO>2.0.CO;2 |
| [7] | Hubbard K G, Goddard S, Sorensen W D, et al. Performance of quality assurance procedures for an applied climate information system. J Atmos Ocean Technol, 2005, 22, (1): 105–112. DOI:10.1175/JTECH-1657.1 |
| [8] | 吴忠义, 马尚风译. 世界气候资料计划文件汇集. 北京: 气象出版社, 1990: 106-109. |
| [9] | Jon Eischeid K, Bruce Baker C, Thomas Karl R, et al. The quality of long-term climatological data using objective data analysis. J Appl Meteorol, 1995, 34: 2787–2795. DOI:10.1175/1520-0450(1995)034<2787:TQCOLT>2.0.CO;2 |
| [10] | You Jinsheng, Kenneth G Hubbard, Steve Goddard.Comparison of air temperature estimates from spatial regression and inverse distance method. http://www.hprcc.unl.edu/manuscripts/. |
| [11] | 屠其璞, 王俊德, 丁裕国, 等. 气象应用概率统计学. 北京: 气象出版社, 1984: 183-186. |
| [12] | Song Feng, Hu Qi, Qian Weihong. Quality control of daily meteorological data in China, 1951—2000:a new dataset. Int J Climatol, 2004, 24: 853–870. DOI:10.1002/(ISSN)1097-0088 |
 2006, 17 (1): 37-43
2006, 17 (1): 37-43