应用气象学报  2005, 16 (5): 561-568   PDF    
引用本文
张正秋, 周秀骥, 李维亮, 孙菽芬. 一些陆面要素非均匀分布对模式计算结果影响的理论分析[J]. 应用气象学报, 2005, 16(5): 561-568.
Zhang Zhengqiu, Zhou Xiuji, Li Weiliang, Sun Shufen. THEORETICAL STUDY ON IMPACTS OF SOME LAND SURFACE ELEMENTS HETEROGENEITIES UPON MODEL OUTPUT[J]. Journal of Applied Meteorological Science, 2005, 16(5): 561-568  
一些陆面要素非均匀分布对模式计算结果影响的理论分析
张正秋1, 周秀骥1, 李维亮1, 孙菽芬2     
1. 中国气象科学研究院, 北京100081;
2. 中国科学院大气物理研究所LASG, 北京100029
2004-04-14 收到, 2004-06-08 收到修改稿.
资助项目: 国家自然科学基金重点项目(40233034)资助。    
摘要: 应用平均参数化方法,从理论上分别研究了地表温度、地面粗糙度、积雪深度和密度非均匀分布对相关物理量计算的影响。结果表明:考虑地表温度的非均匀分布影响后,模式网格上平均地面的长波辐射通量增加,地面饱和水汽压也增加;在相同的地表温度分布变差系数和常温情况下,与长波辐射通量相比,地面饱和水汽压的变化对地表温度非均匀分布较为敏感;地面粗糙度非均匀分布对地面中性曳力系数和BATS型地面积雪覆盖率有一定的影响;积雪深度和密度非均匀分布也对地面积雪覆盖率有一定的影响。
关键词: 陆面要素    非均匀分布    理论分析    
THEORETICAL STUDY ON IMPACTS OF SOME LAND SURFACE ELEMENTS HETEROGENEITIES UPON MODEL OUTPUT
Zhang Zhengqiu1, Zhou Xiuji1, Li Weiliang1, Sun Shufen2     
1. Chinese Academy of Meteorological Sciences, Beijing100081;
2. LAS G, Institute of Atmospheric Physics, CAS, Beijing100029
Abstract: By means of averaged parameterization, a theoretical study is concerned with influences of the heterogeneous distributions of surface temperature, roughness, snow depth and density on their calculated physical quantities.Results indicate that with the surface temperature heterogeneity taken into account, gridded averaged long w ave radiation flux is increased and so is the saturation vapor pressure at surface, which is mo re sensitive to the temperature inhomogeneity compared to the radiation flux for the same coefficient of variation in the temperature distribution and constant temperature condition ;the heterogeneity of surface roughness exert s some impacts on neutral drag coefficient and BATS snow coverage and so does the inhomogeneity of snow depth and density on snow coverage . Key
Key words: Land surface elements     Heterogeneous distribution     Theoretical study    
引言

为了计算简便,在处理复杂问题时,科学家们总是先给定一个假设,然后对这个问题 进行处理。对于气象学家来说,也同样如此。他们把模式网格上的陆面要素分布看成是 均匀的和单一的,然后设计出模式进行数值模拟。然而实际网格上的要素分布既非均匀 也非单一[1],这就使数值模拟结果与实况有一定的差别。有些陆面要素的非均匀分布对 陆面过程有重要影响,是不可争辩的事实。至于这种影响程度有多大,是如何影响的,则 不得而知。对陆面要素非均匀分布的研究方法有多种,可以对实验资料进行分析,也可以 进行数值试验,还可以用数学推导进行证明,其中后者有一定的指导意义。

本文应用张正秋等[2]提出的参数化方法,从理论上分析一些陆面要素非均匀分布的影响。

1 地表温度非均匀分布的影响

由地面通量计算公式可知,地面长波辐射、潜热通量和水汽通量是地表温度的非线性函数,而地面感热通量是地表温度的线性函数,其计算结果与地表温度空间分布变差系数无关。

在地表温度非均匀分布情况下,地表温度在网格元内的变化量与地表绝对温度平均值相比为一小量,不考虑次网格元陆面要素间的相互影响,则地面长波辐射通量在网格元上的平均计算值可以近似写为

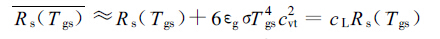
(1)
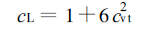
(2)

式(1)、(2)中,σ为斯蒂芬-波尔兹曼常数(W·m-2·K-4),εg为地面比辐射系数(取1.0),Tgs为地表温度,cvt为地表绝对温度在网格上的变差系数。由此可见,如果直接用网格上的平均地表温度计算地面长波辐射,其结果比实际情况偏小。式(1)对实际平均地面长波辐射通量的参数化有非常高的精度[2]。

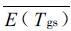
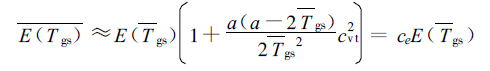
在计算地表面的水汽和潜热通量时,地面饱和水汽压是地表温度的非线性函数。考虑地表温度非均匀分布后,网格上的平均饱和水汽压可以写为

(3)

式(3)中,a=Lv/Rv,Lv为水汽化潜热,Rv为水汽的比气体常数。

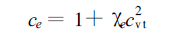
(4)
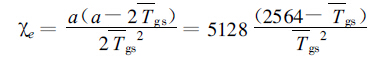
(5)

从上式可以看出,如果直接用网格上的平均地表温度计算地面饱和水汽压,其结果也比实际情况偏小。

从以上的分析来看,在地表温度存在次网格尺度非均匀分布的地区,如果直接用模式网格上的平均地表温度计算地面的长波辐射和潜热通量,就会使计算出的地面向大气输送能量通量比实际偏小。

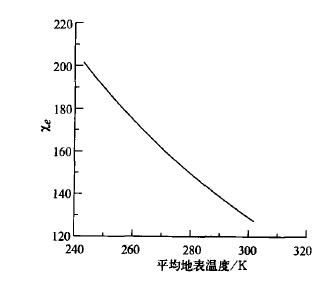
从式(1)～(3)可以看出,考虑地表温度非均匀分布影响后,需要对地面饱和水汽压的计算进行修正,其修正项包括两方面,即χe和变差系数cvt。χe的取值和变化范围如图1所示。从图中可以看出,当平均地表温度增大时,χe的值变小。平均地温自240K至310K,χe的取值范围为200至120 。

图 1. 考虑地表温度非均匀分布影响 后,χe与平均地表温度之间的关系

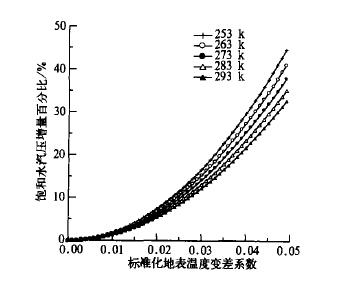
图2给出了地表温度分布变差系数与地面饱和水汽压之间的关系。图中的纵坐标表示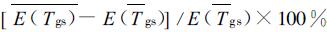,横坐标表示地面绝对温度的空间分布变差系数的变化。标准化绝对地面温度的变化由0～0.05,相当于地表温度0～15K变化幅度。与地面长波辐射通量相比,地面温度非均匀分布对地面饱和水汽压的计算影响较大,前者增长比率为1 +6cvt2,后者增长比率在常规地表温度时至少大于1 +100cvt2。由分析结果可知,与地面长波辐射通量相比,地面饱和水汽压对地面温度非均匀分布较为敏感,因此,地面温度非均匀分布对地面潜热通量的计算有重要的影响。

图 2. 地表温度分布变差系数与地面饱和水汽压之间的关系

2 非均匀分布对模式积雪覆盖率计算的影响

Zeng等[3-4]用统计-动力方法和马赛克法相结合,并利用数值模式研究了粗糙度非 均匀分布的影响,他们针对BATS陆面模式[5-6],对地面中性曳力系数、地面积雪覆盖、地 面通量的阻力系数等非均匀分布进行了参数化,然后与MM4进行耦合,研究它们对地面 通量和降水的影响。其研究基础是给定一种概率密度分布函数(PDF),对PDF函数与以 上要素乘积进行积分计算得到网格上平均值。他们所用的概率分布函数采用的是Giorgi 等1997年提出的方法[7],该密度分布函数中有3个量,即某一陆面要素的平均值、PDF 的半宽长度和高度比率。其中,半宽长度和高度比率是两个独立变量,前者表示要素值变 化范围,后者表示要素值变化的最大值与最小值的比。与Zeng等[3-4]的方法不同,张正秋 等[2]给出了参数化方法分析陆面要素非均匀分布对积雪覆盖率计算的影响。

2.1 BATS型陆面模式中的积雪覆盖率

对于BATS型的陆面模式(如BATS,BEST,CLM[5-6,8-9],地面积雪覆盖率(As)可以表示为

(6)

其中ds为积雪厚度(m),Z0为粗糙度长度(m),k为经验系数。式(6)适用一个点,当考虑粗糙度长度和积雪深度在次网格尺度的非均匀分布时,把式(6)推广到适用一个面的平均计算,上式可以写为

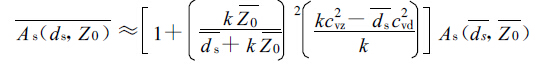
(7)

式(7)中,cvz和cvd分别表示粗糙度和积雪深度的变差系数。

从式(7)可以看出,当只考虑地面粗糙度非均匀分布的影响时,粗糙度非均匀分布使地面积雪覆盖率增加,这一结果与Zeng等[3-4]的结论是一致的。从参数化的方法看,平均参数化方法[2]较简单,而统计-动力方法的参数化方法比较复杂,从Zeng等[3-4]对式(6)积分计算的公式可以看出这一点。

2.2 SiB型陆面模式中的积雪覆盖率

SiB型陆面模式(如SiB,SiB2,SSiB)[10-12]中的地面积雪覆盖率是地面积雪量的线性563 5期张正秋等:一些陆面要素非均匀分布对模式计算结果影响的理论分析函数,由分析可知,它与积雪量在网格上的分布无关[2]。

2.3 CLASS陆面模式中的积雪覆盖率

C LASS中的地面积雪覆盖率是地面积雪量和积雪密度的函数[13],其表达式为

(8)

式(8)中,Ws为单位面积地面积雪质量,单位为kg·m-2;ρs为积雪密度,单位为kg·m-3。当考虑积雪量和积雪密度在次网格尺度的非均匀分布时,上式可以写为

(9)

式(9)中,cvs为积雪密度分布的变差系数。

2.4 基于熵最大原理得到的积雪覆盖率

Zhang等[14]由熵最大原理推导地面积雪覆盖率可以表示为

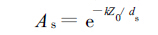
(10)

式(10)中,k为经验系数。通过对式(10)近似展开,可以得到式(6)的形式[14]。

考虑地面粗糙度和积雪深度非均匀分布,由式(10)可以得到模式网格上积雪覆盖率 的计算公式,即

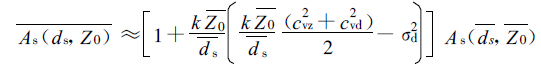
(11)

式(11)中,cvz和cvd也分别表示粗糙度和积雪深度变差系数,与式(7)中的意义相同。可以看出,式(11)和(7)都表示了粗糙度的非均匀分布使网格上平均地面积雪覆盖率增加,而积雪深度的非均匀分布使积雪覆盖面积减少。

3 粗糙度非均匀分布对中性曳力系数计算的影响

地面粗糙度不仅与地表积雪覆盖相联系,而且与曳力系数(CD)的计算相关。在BATS中用CD来对植被叶簇中的风以及空气阻力进行系数参数化[5]。分析说明地面粗糙度次网格非均匀分布对中性曳力系数CDN的影响。

Zeng[3-4]曾用统计-动力方法研究了地面粗糙度非均匀分布对CDN的影响。在给定不同的PDF半宽度和比率时,计算了CDN的值。结果表明,地面粗糙度越不均匀,CDN的平均值越大。但此计算方法中有两个参数需要确定,即PDF半宽度和比率需要确定,而且计算公式较为复杂。

在不考虑近地面参考高度变化的情况下,模式网格上平均中性曳力系数可以表示为

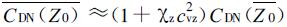
(12)

式(12)中,

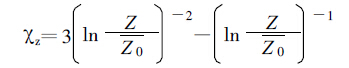
(13)

式(13)中,Z为参考高度。

为了更清楚地看到地面粗糙度的非均匀分布对模式网格上平均CDN的影响,取Z=10 m,得到χz与的关系(图3)。从图3可以看出,当≈0.5时,χz=0,也就是说,当>0.5时,CDN的变差系数使其平均值增大,反之,则减小。总的来看,χz是的增函数。

图 3. 考虑地表粗糙度非均匀分布影响后,χz与Z0之间的关系

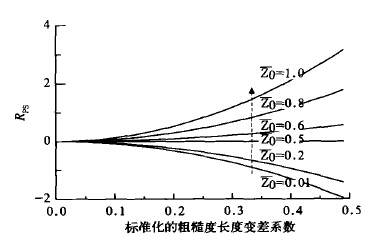
图4给出了在不同平均粗糙度下,地面粗糙度分布的变差系数对平均中性曳力系数的影响。图中横坐标为粗糙度变化的变差系数,纵坐标为曳力系数在考虑非均匀分布影响后增加相对百分比率,即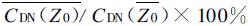。从图中可以看出,当>0.5时,CDN随粗糙度变差系数的增加而增加,反之,CDN随粗糙度变差系数的增加而减小。可以看出,当粗糙度变差系数一定时,随着平均粗糙度增大,CDN值是增加的。

图 4. 地表粗糙度长度分布变差系数与中性曳力系数之间的关系

4 地表温度非均匀分布影响随机函数试验

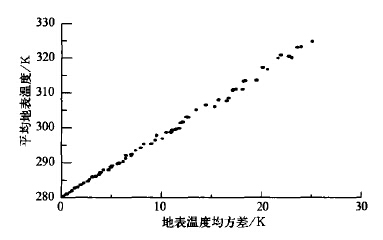
用随机函数进一步研究地表温度非均匀分布对地面饱和水汽压的影响,以便检验第1节中的理论分析结果的正确性。在给定一个初值后,随机函数可以生成0～1范围内的一组数。为了得到平均地表温度值和均方差,通过任意给定一个数乘以不同的随机数得到一组试验地表温度值,每一组产生400个温度值。然后,由这些值计算得到一个平均地表温度值和均方差。这样,通过设定不同的初值和任意给定数,我们可以得到多个平均地表温度值和均方差。由随机函数产生的地表温度均方差与平均值之间的关系如图5所示。从图5可以看出,随着地表温度平均值增大,地表温度变化的均方差也增大,有一种近似的线性关系,这反映了一种随机规律。可以用以下的数学表达式来描述,即

图 5. 由随机函数产生的地表温度均方差与平均值之间的关系

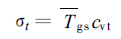
(14)

式(14)中,cvt为地表温度的变差系数,相当于随机函数产生的变差系数。

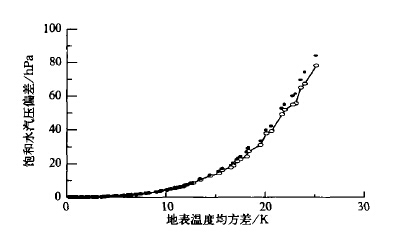
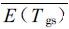
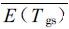
图6给出了次网格尺度地表温度非均匀分布对模式中地面饱和水汽压计算结果的影响。与图5类似,图中的实心圆点是由随机函数发生400次得到的计算结果。对于每个随机温度值,先分别计算饱和水汽压,然后对饱和水汽压平均,得到;对随机温度平均,得到Tgs,再计算出E(Tgs),图中的实心圆点是与E(Tgs)的差值。图中的空心圆曲线是用随机函数产生的温度变化均方差用下式计算得到的,即

图 6. 地表温度非均匀分布对模式中地面饱和水汽压计算结果的影响

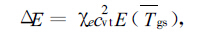
(15)

式(15)中,χe用式(5)来计算。

从图6可以看出,用参数化公式计算得到的空心圆曲线与图中的实心圆点较接近,说明参数化方法的正确性,也说明随着地表温度均方差的增大,与把地表温度看成均匀的结果相比,二者的偏差越来越大。这也说明了前面分析的正确性。通过计算可以得到,在地表温度均方差为10 K时,实际的偏差值为4.3 hPa,参数化方法得到的偏差值为4.2 hPa,二者之差为0.1 hPa ;在地表温度均方差为20 K时,实际的偏差为39.7 hPa,参数化方法得到的偏差为38.0 hPa,二者之差为1.7 hPa,可以看出,地表温度均方差越小,参数化方法得到的计算结果与实际的结果越接近,同时也可以看到,地表温度的非均匀分布对模式网格元上平均饱和水汽压的计算有较大的影响。

对于一个模式网格来说,地表温度的变化幅度为20 K是很少见的,因此我们可以用地表温度的变差系数来描述地表温度的非均匀分布对地面饱和水汽压等的影响。同时,也可得出如下的结论,即地表温度分布越不均匀,现有模式对地面饱和水汽压等的计算误差越大。

5 小结

实际情况下,陆面要素非均匀分布的影响是各种各样的,本文只研究了几种要素非均匀分布的影响,得到以下结果:

(1) 考虑地表温度的非均匀分布影响后,模式网格上平均地面的长波辐射通量增加,地面饱和水汽压也增加。在相同的地表温度分布变差系数和常温情况下,与长波辐射通量相比,地面饱和水汽压的增加比率较地面长波辐射通量的增加比率大,因而地面饱和水汽压的变化对地表温度非均匀分布较为敏感。由于在模式计算中,地面饱和水汽压是计算水汽通量和潜热通量的重要物理量,由此可推断,地表温度的非均匀分布对地面水汽通量和潜热通量有重要的影响。

(2) 地面粗糙度非均匀分布使BA TS型地面积雪覆盖率增大,积雪深度的非均匀分布使BATS型地面积雪覆盖率减小;地面积雪密度的非均匀分布使C LASS的地面积雪覆盖率增大。

(3) 当地面粗糙度长度较小时,地面中性曳力系数随粗糙度长度的变差系数的增加 而增加,反之,随粗糙度的变差系数的增加而减小。

总之,考虑陆面要素非均匀分布的影响后,一些陆面通量的计算结果可以得到一定改进。

参考文献
[1] 孙菽芬, 金继明. 陆面过程模式研究中的几个问题. 应用气象学报, 1997, 8, (增刊): 50–57.
[2] 张正秋, 周秀骥, 李维亮. 陆面气象要素非均匀分布对模式计算结果影响及其参数化初步探讨. 应用气象学报, 2002, 13, (6): 641–649.
[3] Zeng Xinmin, Zhao Ming, Su Bingkai, A numerical study on effects of land surf ace heterogeneity from “ Combined Approach” on atmospheric process. Adv Atmos Sci, 2000, 17, (1): 103–120. DOI:10.1007/s00376-000-0047-0
[4] Zeng Xinmin, Zhao Ming, Su Bingkai, A numerical study on effects of land surface heterogeneity from “Combined Approach” on atmospheric process. Adv Atmos Sci, 2001, 7, (2): 241–255.
[5] Dickinson R E, Henderson-S ellers A, Kenndy P J, et al.Biosphere-Atmosphere Transfer Scheme(BATS)for the NCAR Community Climate Model, NCAR Tech.Not e-275 +S TR, USA, 1986.
[6] Dickinson R E, Henderson-Sellers A, Kennedy P J, et al.Biosphere Atmosphere T ransfer S cheme (BATS)Version 1e as Coupled t o the NCAR Community Climate Model.NCAR Tech.Note TN-387 +ST R, National Cent er for Atmospheric Research, Boulder, CO, USA, 1993.
[7] Giorgi F, An approach for the representation of surf ace heterogeneity in land surface models. Mon Wea Rev, 1997, 125, (8): 1885–1899. DOI:10.1175/1520-0493(1997)125<1885:AAFTRO>2.0.CO;2
[8] Pitman A J, Yang Z-L, Cogley J G, et al.Description of Bare Essential of Surface Transfer for the Bureau of Meteorology Research Cent re AGCM.BMRC Research Report, 1992.1～127.
[9] Dai Yongjiu, Zeng Xubin, Dickinson Robert E.Common Land Model (CLM), Techni cal Documentation and User' s Guide, NCAR Technical Not e, 2001.
[10] Sellers P J, Mintz Y, Sud Y C, et al . A Simple Biosphere Model(SiB)for use within General Circulation Models. J Atmos Sci, 1986, 43, (6): 505–531. DOI:10.1175/1520-0469(1986)043<0505:ASBMFU>2.0.CO;2
[11] Sellers P J, Los S O, Tucker C J, et al . A revised land surface parameterization (SiB2)for atmospheric GCM s. J Climate, 1996, 9: 706–737.
[12] Xue Y, Sellers P J, Kinter J L, et al . A simplified biosphere model for global climate studies. J Climate, 1991, 4: 345–365. DOI:10.1175/1520-0442(1991)004<0345:ASBMFG>2.0.CO;2
[13] Verseghy L D, CLASS-a Canadian land surface scheme for GCM. Soil Model.Int J Cl imat e, 1991, 11: 111–133.
[14] Zhang Zhengqiu, Li Weiliang, Entropy and parameterization of non-uniform distribution of precipitation. Acta Meteor Sinica, 1998, 12, (3): 335–344.