2. 中国气象科学研究院, 北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
现代气象学始于对大气观测的天气分析,即对天气图的分析以及据此对未来天气的预报;另一方面,则是应用力学来试图解释所发现的天气现象。于是在20世纪初期开始了大气动力学研究,如运用流体力学发展了环流理论;20世纪30年代,应用波动力学发现了Rossby波,开创了地球物理流体力学;20世纪50年代初实现了基于正压模式的数值天气预报,因此动力学在大气科学一直处于主导地位[1]。20世纪80年代以来,大气非线性动力学研究取得了重大进展,而非线性热力学进展却不那么显著,滞后于前者。同时,大气非线性动力学与非线性热力学利用不同的理论体系和方法进行研究,各自独立地发展着,很少涉及其间的联系。
大气热力学在20世纪70年代以前其基础是经典热力学,而且仅视为大气动力学的一个补充,如40年代的热成风发展理论,提出了热成风概念及其力学表达;与此同时在位温、假相当位温等概念的基础上发展了热力学图表,供天气预报实践使用。20世纪70年代以来,物理学在热力学方面取得了突破性进展,Prigogine等提出了耗散结构的概念和理论,形成布鲁塞尔学派,并因此获得了诺贝尔奖,这也推动了大气热力学的发展。例如发展了大气系统的熵平衡理论和热力学熵模式,探讨了大气中的自组织现象。提出了全球气候是一种最小熵交换系统的概念,由此构造全球模式对现在气候进行了模拟。耗散结构是指当系统处于远离平衡态时,通过系统与外界进行能量和物质交换而形成且维持的一种由非线性机制产生的有序结构,即在非平衡态下宏观系统的自组织现象。台风、龙卷风无疑是一种耗散结构,因为必须不断从周围环境中吸取能量才能生存和发展。封国林等运用观测资料分析表明,它们还是一种自组织临界态系统[2]。
20世纪80年代起,随着气候和全球变化研究的进展,热力学被放到越来越重要的位置上,因为热力学因子对大气和地球系统的长期行为更为重要。这样研究大气的非平衡态热力学尤显得迫切,在这期间获得了若干重要学术成果,文献[3]对此作了评述。本中将对1980年以后尤其是20世纪90年代大气热力学进展作简要回顾并对若干重要问题进行评述。
1 非传统大气热力学问题1982年至20世纪90年代初,在苏联解体、冷战结束前,地球科学家对所谓的“核冬天”进行了研究。即研究一旦全球核战争爆发,除了核武器造成的破坏外,由于大规模核战争将引发大范围的燃烧,在乡村,森林、草原和庄稼着火;在城市,贮存的石油、天然气、煤及其他易燃品会引起火灾,浓烟和尘埃冲入大气,有的甚至到达平流层。大气环流把它们散布到全球高空,其结果,烟尘遮断阳光,破坏了地球热平衡,使全球气温下降,甚至在夏天也可能降到冰点以下,出现了类似冬天的景观。Cao等用全球数值模式对此“虚拟”状态进行了模拟并对多可能情景进行了研究[4],也从热力学方程出发构建了一维热平衡模式,对不同的可能核战情景及其降温效果进行了研究。核冬天虽没有发生,却向我们提出了非传统的大气热力学问题。
人类活动影响着气候,尤其是当今大规模的人类活动,随之而来的气候现象不少需从热力学角度来研究,如全球增暖和城市热岛效应等。由工业排放等造成大气中温室气体增加,导致温室效应使全球增暖,这已引起政府、公众、科学界的严重关注。显然温室效应是热力学效应,物理学家对此也产生了浓厚兴趣[5],这提示我们要用前沿科学成果来探讨;用非平衡态大气热力学来研究它,会有更大的潜力和意想不到的结果[6]。参与全球增暖的有二氧化碳、二氧化硫、氮氧化物、甲烷等温室气体,因此,人们要研究这些温室气体的化学热力过程,及它们对气候状态的热力强迫作用。目前对全球增暖的模拟和预测是用全球耦合模式进行的,其空间分辨率和物理过程细致化都达到了高水平[7]。需要指出,这类模式是“普适”的,即它不限于模拟全球增暖,还可以模拟其他气候现象。这里,我们提出了构建模拟全球增暖模式的另一种思路,即以非平衡态热力学为基础来设计模式。这方面虽已有所理论性研究成果,但要建立和发展一个突显热力学作用的数值模式,仍需进行深入探讨。
城市热岛效应直接影响城市的建筑、交通、住房乃至人们的日常生活。所以在全球增暖的研究中,城市热岛效应也是热点论题之一。例如,在5次IPCC (联合国政府间气候变化委员会) 关于气候变化的科学评估报告中对城市热岛效应都有专门叙述[8]。由于人们怀疑全球增暖可能并非来自温室气体效应,而是来自城市热岛效应,这是因为有长期记录的测站都在城市,这就促进了对城市热岛效应的研究。研究表明,因城市热岛效应局限在小范围的局部地区,它对全球和半球气温增加贡献是十分有限的;估计在1900~1999年期间对全球和半球陆地气温序列的影响不超过0.05 ℃。20世纪90年代对全球增暖的研究阐明夜间增温大,白天增温小,导致日较差减小,即发现最高最低气温的非对称变化的事实[9]。城市热岛效应、沙漠绿洲冷岛效应和最高最低气温非对称变化等问题都属于大气热力学面对的新问题。
沙漠绿洲是在有水源的沙漠中出现的,由于植树造林的人类活动,出现了人为沙漠绿洲。沙漠绿洲有着冷岛效应,人们对此进行了观测和模拟研究[10]。数值试验研究表明,绿洲与沙漠的相互作用是一复杂的非线性过程,绿洲系统与沙漠环境间的能量和质量 (水汽) 交换,导致绿洲的冷岛效应。冷岛效应是大气-环境-生态耦合系统的自组织产物,系统获得负熵流是产生和维持冷岛效应的热力学机制,冷岛结构是一种典型的耗散结构。对大气耗散结构的研究显然是非平衡态热力学的丰硕成果之一。
2 构建大气数值模式的新视点大气受太阳辐射和地球旋转驱动,是一个热力-动力系统,大气从不重复它过去的行为,是一个混沌系统。一般来说,天气指大气的瞬时状态,而气候是大气的平均状态。或者可以作这样的推断,天气是以动力学运动为主导的的大气状态,而气候则是以热力学运动为主导的大气状态。从系统变化在时间方向的承续性,即记忆性来说[11],天气是以动力记忆占优势的大气状态,而气候是以热力记忆占优势的大气状态。根据这种观点,显然需要调整当前数值模式中把动力方程和热力方程联立,即等同对待的数学处理,应在天气预报中突显动力学作用,而在气候预测中突显热力学作用。这或许是提高数值模式预报准确率的一个潜在途径,可以说,当前通行的数值模式是突显动力学作用的模式。尽管关于突显动力学作用或热力学作用的提法尚需进一步讨论和探索,但至少让我们从另一种角度来审视现有的数值天气预报模式和气候数值模式。
预报通常分为短期天气预报、中期天气预报和长期天气预报乃至气候预报;从数学角度来划分,按冯·纽曼的观点,数值预报相应地分为微分方程的初值问题,初、边值混合问题和边值问题。若从物理角度来进行划分,则把预报从其主要制约物理过程分为以动力学为主的问题和以热力学为主的问题;相应构造和设计的模式,称前者为突显动力学作用的模式,后者为突显热力学作用的模式;或分别称为动力主控模式和热力主控模式。
怎样设计突显热力学作用的模式呢?大气非平衡态热力学为构建这类模式提供了一个理论基础。由于非平衡态热力学的理论框架和数学表达与大气动力学差异甚大,因而据此建立的数值模式与现有的模式将是不同的,这类数值模式的计算格式和物理过程的表达都会有别于现有模式。在突显热力学作用的模式中,描述不可逆过程热力学第二定律的熵平衡方程是一个最基本的方程,它描述大气系统的发展方向。而动力学方程组 (动量守恒方程、连续性方程、水汽方程等) 数学上表达了一个强迫耗散系统,描述大气系统的发展细节。大气动力过程中的动量通量、热量 (辐射、潜热) 通量、水汽通量和相变速率在熵平衡方程中表现为描述不可逆过程进展速率的热力学流。这种差异使得发展这类模式会遇到原理上、计算上的困难,但其发展前景是诱人的,潜力是巨大的。
为了整合热力作用和动力作用,基于大气系统的物理特性引入所谓“动力熵”的概念,从而导出大气系统熵平衡方程的新表达式[6],即
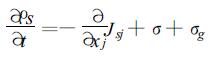
|
(1) |
式 (1) 中,ρ为密度,s为单位体积的熵,Jsj为熵流,σ为熵产生,σg为动力熵产生。σg源自大气微团组分的动能、牛顿力对组分的作功等动力特性。式 (1) 比一般熵平衡方程多了σg项,即在熵平衡方程中融入了大气动力特性,从而会克服将非平衡态热力学应用于大气系统的困难。与式 (1) 相应,大气动量守恒方程 (牛顿笫二定律) 表达为
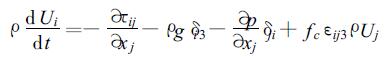
|
(2) |
式 (2) 中,Ui为速度分量,i=1,2,3;τij为应力张量;ρ为密度;δij为单位张量,当i=j时,δij=1,否则δij=0;εijk为取{1,0,-1}的参数;fc为柯氏参数,p为压力,g为重力加速度,t为时间坐标,xj为空间坐标。
由于式 (1) 和 (2) 均是一个带时间微商项的微分方程,因此可以转变为一个差分-积分方程,即可以应用自忆性原理来进行求解[11]。由此可以研究大气的热力记忆性,并从熵变角度来对天气和气候变化进行模拟和预报。
数值气候模式的计算结果表明,现有模式已能对气候平均状态作出相当逼真的模拟,若干敏感性试验,如温室效应,已有实际应用价值;但对季节预报、年际预报的预报技巧相当低。这种情况的一种可能解释是,现有数值气候模式是一种突显动力学作用的模式,由于大气是一个混沌系统,对初值很敏感;因此每年太阳辐射的季节变化或年际变化的差异虽不大,但对气候变化的影响却不小。如果我们设计突显热力学作用的气候模式,有可能改进当前对气候变化的数值预报水平。
大气科学中所关心的预报问题,是和大气系统的稳定性问题相联系的。因为在一个系统的发展进程中,现在或近期观测到的相对稳定的大气状态,正是非平衡热力学的一个定态。预报要报出现有系统的延续,更重要的是要报出系统何时失稳,或者说新系统状态的发生和发展。而这正是非线性热力学所研究的系统稳定性问题。非线性热力学稳定性分析为天气预报、气候预测以及人工影响天气开辟了一种新思路和方法,例如,天气转型、气候突变、环境干旱化等,又如人工增雨、人工消雹、人造小气候或局地气候的人工影响等。我们要研究的是用最小的能量、物质改变天气或气候系统的稳定性,从而触发天气或气候系统内部能量或物质状态改变,达到人工影响天气和气候的目的。显然这也是一个有代表性的热力系统稳定性问题,这在经典大气热力学中几乎没有触及。运用突显热力学作用的数值模式会对这类预报问题作出新的研究成果。
用去趋势涨落分析 (Detrended Fluctuation Analysis,DFA) 对百年记录日气温、千年模拟日气温和百余年东亚季风变化等研究表明,气象要素和大气现象具有长程记忆特性[12~13],这为可预报性提供了客观基础。关于大气系统的短程记忆和长程记忆的研究及其热力学性质的探讨,将为大气热力学理论的预报应用和设计突显热力学作用的气候模式提供观测基础。进一步应用自忆性原理,就有可能发展一种新的气候系统模式。
3 大气热力学的发展热学中发展的非平衡态热力学是对物理和化学现象的研究成果,可以认为这些现象是实验室尺度的物理和化学现象,他们所研究的热力系统是以分子为基本粒子的宏观系统,其耗散过程是分子粘性效应。而大气热力系统是空气微团组成的地球尺度的宏观系统,其耗散过程是湍流粘性效应,并受重力场和柯氏力等动力因子和热力层结的热力因子控制。因此,发展适合大气固有特征的热力学,把物理、化学中的非平衡态热力学应用到大气科学中,是学科发展迫切要求的[6]。由于两者的控制方程和系统特征不同,因此这是一项极具有挑战性的科学研究。
在大气科学中,表达热力学第一定律的方程是构建数值模式的基本方程,而热力学第二定律在大气力学中似乎不占重要地位。实际上热力学第二定律表示了一个方向矢,即系统的热力过程是不可逆的,表示了系统运动的时间趋向,具有重要的物理内涵。基于热力学第二定律,可以在数值计算中构造合理的差分格式,研究表明,这种具有物理含义的差分格式确能提高天气预报准确率[14]。从熵平衡观点来研究气候系统始于20世纪80年代,90年代取得了新的进展。如研究气候常定态时的熵产生,根据卫星观测资料计算源于短波辐射和长波辐射的熵通量。用简单垂直灰模型研究气候平衡态的结果表明,地球气候存在一个唯一的气温分布和对流-辐射通量分布,它代表了一个最大熵增态,而这一分布类似于现在气候。这表示,现在大气热通量的全球平均态以及另一些行星的现有状态,是以其可能最大速率的熵增方式达到稳定的[15]。
目前,已出版的大气热力学专著几乎都基于经典力学的范畴[16~17]。关于非平衡态热力学在大气科学中应用的研究已取得了若干进展,如研究大气中各种系统的熵平衡,研究大气中的耗散结构[18~19]等;大气系统以及大气中的子系统,如温带气旋、热带气候、锋区等,都处于非热力平衡态[20],具有耗散结构特征,文献[18]对大气中的耗散结构进行了系统的论述。20世纪90年代以来,国内外大气科学领域对大气熵理论[21~23]、求解热力学方程的福克-普朗克 (Fokker-Planck) 途径[24]等方面都进行了有成效的研究,丰富了非线性大气热力学。把动力变量和动力方程变换为熵表达形式,也已有这方面的尝试[25],其思路是直接把动力变量类比地看作为一个温度变量来定义熵函数;这与导出式 (1) 的思路和步骤是不同的。大气的外来能量主要源于太阳辐射,少量通过火山爆发等来自地核,因此,大气过程是一种不可逆过程,对此人们已进行了理论和模式研究,其中包括运用简单模式和全球模式进行的对热响应、热惯性、热耗散和非线性过程等问题的研究[26~29]。
由于我们对大气的热力学作用和热力过程了解还不够,大气非平衡态热力学理论研究也处在初创期,任重而道远。20世纪70年代以来,已尝试从热力熵理论来建立气候系统模式[30~31],这样有可能不必在模式中涉及所有尺度上的物理过程而建模。但从热力-动力熵理论来发展大气数值模式更具有吸引力,因为大气的动力过程对描写大气运动是非常重要的。相信,随着当今其他学科的飞速发展,特别是物理、化学和计算数学的发展,在不久的将来,定能建立和发展突显热力学作用的数值模式。
| [1] | 伍荣生. 大气动力学. 北京: 气象出版社, 1990: 1-338. |
| [2] | 封国林, 曹鸿兴. 大型涡旋自组织临界态的观测证据. 热带气象学报, 1994, 10, (2): 154–160. |
| [3] | 曹鸿兴, 蔡善皋. 非平衡统计力学在大气科学中的应用进展. 高原气象, 1985, 4: 361–371. |
| [4] | Cao Hongxing, Wang Yongzhong, Lin Yunmei, Climatic effects of nuclear war in China. Chinese Journal of Environmental Sciences, 1993, 5, (3): 230–240. |
| [5] | 赵凯华, 罗蔚茵. 热学. 北京: 高等教育出版社, 1998. |
| [6] | 胡隐樵. 大气热力动力学导论--大气非平衡态线性和非线性热力学. 北京: 地质出版社, 2002: 1-406. |
| [7] | Summi A, Kimoto M, Emori S, et al. Model Development for the Global Warming Prediction by Using the Earth Simulator. Procedings of the International Symposium on climate Change, 31 March-3 April 2003, Beijing, China. WMO/TD-No.1172. 76-79. |
| [8] | Houghton J T, et al. Climate Change 2001, The Scientific Basis. Cambridge: Cambridge University Press, 2001. |
| [9] | Xie Zhuang, Cao Hongxing, A symmetric changes in maximum and minimum temperature in Beijing. Theor Appl Climatol, 1996, 55: 151–156. DOI:10.1007/BF00864710 |
| [10] | 胡隐樵, 高由禧. 黑河实验--对干旱地区陆面过程的-些新认识. 气象学报, 1994, 52, (3): 285–296. |
| [11] | 曹鸿兴. 动力系统自忆性原理--预报和计算应用. 北京: 地质出版社, 2002: 1-192. |
| [12] | Fraedrich K, Blender R, Scaling of atmosphere and ocean temperature correlation in observations and climate models. Physical Review Letters, 2003, 90, (10): 108501–1. DOI:10.1103/PhysRevLett.90.108501 |
| [13] | Cao Hongxing, Blender R. He Huizhong, et al. Long Memory of East-Asian Monsoon and Its Implication for Prediction. In the DVD Proceedings of 1st International CLIVAR Science Conference, 21-25 June 2004, Baltimore, USA. |
| [14] | 柳崇健, 刘英, 康红文. 一种新的物理耗散技术及其在中尺度数值天气预报模式中的应用. 中国科学 (D辑), 2002, 32, (3): 255–264. |
| [15] | Ozawa A, Ohmura A, Thermodynamics of a global-mean state of atmosphere-a state of maximum entropy increase. J Climate, 1997, 10, (3): 441–445. DOI:10.1175/1520-0442(1997)010<0441:TOAGMS>2.0.CO;2 |
| [16] | Tsonis A A, An Introduction to Atmospheric Thermodynamics. Cambridge: Cambridge University Press, 2002: 1-172. |
| [17] | Curry J A, Webster P J, Thermodynamics of atmospheres and Oceans. London: Academic Press, 1999: 1-468. |
| [18] | 柳崇健. 大气耗散结构理论. 北京: 气象出版社, 1988. |
| [19] | 钱维宏. 大气中的耗散结构与对流运动. 大气科学, 1992, 16: 84–91. |
| [20] | 曹鸿兴. 评专著《大气热力动力学导论--大气非平衡态线性和非线性热力学》. 应用气象学报, 2004, 15, (6): 767–768. |
| [21] | 张学文. 组成论. 合肥: 中国科学技术大学出版社, 2003: 202-212. |
| [22] | Brien D M, A yardstick for global entropy-flux. Quart J R Meteor Soc, 1997, 123: 243–260. DOI:10.1002/(ISSN)1477-870X |
| [23] | Duane G.S, Curry J A, Entropy of a connecting water-air system and the interpretation of cloud morphogenesis. Quart J R Meteor Soc, 1997, 123: 605–629. DOI:10.1002/(ISSN)1477-870X |
| [24] | Feng Guolin, Cao Yongzhong, Cao Hongxing, Air-sea stochastic climate model and its application. Chinese J Comput Phys, 2001, 18, (1): 57–63. |
| [25] | Egger J, Numerical generation of entropies. Mon Wea Rev, 1999, 127: 2211–2216. DOI:10.1175/1520-0493(1999)127<2211:NGOE>2.0.CO;2 |
| [26] | Wu Q, North G R, Climate sensitivity and thermal inertia. Geophys Res Lett, 2002, 29, (15): 2.1–2.3. DOI:10.1029/2002GL014864 |
| [27] | Barsugli J J, Battisti D S, The basic effects of atmosphere-ocean thermal coupling on middle-latitude variability. J Atmos Sci, 1998, 55: 477–493. DOI:10.1175/1520-0469(1998)055<0477:TBEOAO>2.0.CO;2 |
| [28] | Gade H G, Gustafson K, Application of classical thermodynamics principle to study of oceanic overturning circulation. Tellus, 2004, 56A, (4): 371–387. |
| [29] | Nicolis C, Irreversible thermodynamics of a simple atmospheric flow model. Int J of Bifurcation and Chaos, 2002, 12, (11): 2557–2566. DOI:10.1142/S0218127402006035 |
| [30] | 曹鸿兴. 气候动力模式与模拟. 北京: 气象出版社, 1994: 165-205. |
| [31] | Stephens G L, O, Brien D M, Entropy and climate II:simple models. Quart J R Meteor Soc, 1995, 121: 1773–1796. DOI:10.1002/(ISSN)1477-870X |
 2005, 16 (4): 554-416
2005, 16 (4): 554-416

