2. 北京大学物理学院, 北京 100871
2. School of Physics, Peking University, Beijing 100871
有关气候的年际及年代际振荡问题是目前气候研究的一个热点。Allan及Reason等人的研究表明,2~2.5年、2.5~7年的年际振荡及11~13年、15~20年的年代际振荡在全球气候系统中最突出[1~2]。其他研究也证实了准两年至6~7年振荡在气候要素中存在的事实[3~4],并被认为是气候系统内部的变化和ENSO振荡的结果。有研究表明,大气和海洋变化均具有10~20年或更长时间尺度的年代际振荡[5],在气温和降水气候要素中也普遍存在10~20年尺度的振荡。长江中下游梅雨是东亚季风系统的重要成员,也是全球性季节转变过程中的特有现象。有关梅雨的研究我国学者做了许多有意义的工作,徐群等人的研究涉及到梅雨的年际和年代际变化[6~7],发现梅雨量不仅存在2~3年、6年、8~9年的周期变化,同时也存在22~23年、35~38年和72年等长周期的变化。
魏凤英等最近利用徐群定义的1885~2000年长江中下游梅雨特征量资料[8],分析了近百年梅雨入梅早晚、梅雨期长短、梅雨强弱的年际及年代际变化特征和相互关系,发现长江中下游梅雨出梅日期和梅雨期长度的年际变差很大,从而导致长江中下游夏季旱涝频繁发生,其中控制入梅、出梅和梅雨期长度的5~6年周期变化的气候因素相同。分析还表明,长江中下游梅雨在近116年中经历了6个异常气候阶段。这一工作是用统计方法从一个层次上对长江中下游梅雨特征量的年际和年代际变化特征进行分析的,且没有涉及梅雨的年际及年代际变化随时间演变的特征。事实上,气候系统存在多种尺度层次的变化,而且在不同时期振荡的强弱也可能存在差异,因此有必要从多层次的角度对近百年长江中下游梅雨的年际及年代际振荡及随时间演变特征进行研究。本文首先推导证明出Morlet小波系数通过零的点即为突变点,然后用小波变换和统计检验相结合的方法检测近百年来长江中下游梅雨强度变化的多尺度层次的气候突变点,进一步利用小波能量密度及其方差研究梅雨强度年际/年代际振荡的演变特征。
1 多尺度气候突变点检测和气候振荡能量计算本研究使用的资料是徐群定义给出的1885~2000年长江中下游梅雨强度[6~7]。分析方法为Morlet小波变换[9],其形式为
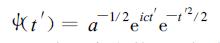
|
(1) |
式 (1) 中,t′=(t-t0)/ a,其中a>0,为尺度参数;t0为时间位置参数;c为常数。ψ(t′) 反映的是波长约为2 a的波动信号。对于任意要研究的一维信号f(t) 的小波变换可以表示为
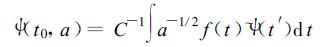
|
(2) |
式 (2) 中,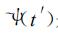
刘太中等证明墨西哥帽形式的小波系数穿过零的点即为f (t) 的突变点[10]。Morlet小波虽然形式上比墨西哥帽小波复杂,但是用同样的方法可以检测f(t) 各时刻的奇异性,得到多尺度层次的突变点。我们可以导出式 (1) 是
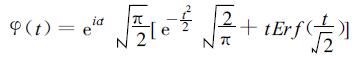
|
(3) |
的二阶导数。式 (3) 中,Erf(z) 是高斯分布的积分,由
利用式 (2) 的小波变换可以计算f(t) 在尺度a全域上的能量密度

|
(4) |
式 (4) 中,
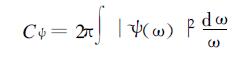
|
依据E(a) 我们可以考察f(t) 的小波能量密度随频率的变化。信号f (t) 在时间位置t0的能量密度为

|
(5) |
依据E(t0) 可以分析f(t) 的小波能量密度随时间的变化。同样,我们可以计算f (t) 在某一尺度a1~a2上的能量密度
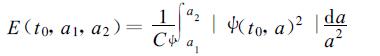
|
(6) |
依据E(t0,a1,a2) 可以研究各频率的能量密度随时间的变化。
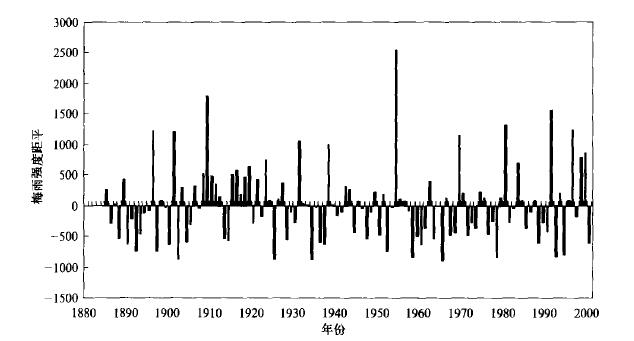
2 梅雨强度的多尺度气候突变从图 1给出的1885~2000年长江中下游梅雨强度的距平变化可以看出,近百年的梅雨强度含有多尺度层次的变化。使用普通统计检验方法,如t检验、MK统计量等,仅能研究气候序列一个层次的突变。利用小波变换和统计检验相结合的方法,不但可以得到多尺度层次的谱系结构,也可以对谱系结构的突变点进行统计显著性检验。
|
|
| 图 1. 1885~2000年长江中下游梅雨强度距平 | |
图 2为梅雨强度时间尺度a取为60年的小波变换。由图 2可以清楚地看到,在1941年处的小波系数通过零点,按照小波的奇异特性可知,梅雨强度在1941年发生了突变。经统计,发生突变的前一时段1885~1941年距平平均值为22.31,后一时段的1942~2000年距平平均值为-21.55。突变前后两种状态分别对应非线性系统的梅雨强和弱的吸引子。从1941年起梅雨由强突变到弱,而且这种突变超过了显著性水平α=0.05的检验,也就是说,从大尺度而言,近百年长江中下游梅雨强度以1941年为界分为强与弱两种状态。

|
|
| 图 2. 梅雨强度时间尺度a为60 a的小波变换 | |
时间尺度a取为40年时,小波系数通过零点的突变点有4个,梅雨强度的大尺度强和弱时段中均含有较小尺度强与弱的吸引子。时间尺度a取为20年时,小波系数通过零点的突变点增加到7个,若时间尺度a取为10年时,出现间隔更小尺度的数十个突变点,这样就构成了多尺度层次的谱系结构。表 1列出了以时间尺度60年、40年和20年的突变点划分出的时段、对应的距平平均值和突变点前后两时段的t统计量值 (括号内值为显著性水平α=0.05的tα值)。
|
|
表 1 多尺度层次的突变点及其检验 |
由表 1可见,就40年的尺度而言,在1885~1941年期间的梅雨变化中含有两个相对弱和一个相对强的吸引子,即1885~1903年和1928~1941年期间处于梅雨较弱时期,1904~1927年的24年间梅雨处于比较强的时期;在1942~2000年期间的梅雨变化中含有一个相对弱和一个相对强的吸引子,即1942~1990年期间梅雨较弱,1991~2000年期间处在近百年最强的时期。总之,以较大尺度来划分,近百年梅雨强度变化可分为以上5个阶段。
从20年的尺度来看,1885~1941年期间的梅雨变化中在原基础上又增加了一个较强的吸引子,即在1904~1912年期间的梅雨较强;1941~2000年期间又增加了一个相对强和一个弱的吸引子,即1942~1967年期间梅雨较弱,而在1968~1985年期间梅雨转变为较强,1986~1990年又猛然回落,1991~2000年这10年处在近百年梅雨最强的时期。
3 梅雨强度年际及年代际振荡的演变特征图 3给出了1885~2000年长江中下游梅雨强度在尺度a全域上的能量密度图像。图中较深颜色的部分表示相应频率的能量密度较强,颜色较浅部分表示对应频率的能量密度较弱。依据这张图可以考察梅雨强度不同尺度振荡的变化特征。由图 3可以看出,在10年以上的年代际尺度上,20世纪初至20世纪20年代初、20世纪50年代初至60年代末以及90年代这3个时段在10~20年时间尺度的能量密度较强,即振荡较强。对应20~30年时间尺度,在20世纪40年代中期至70年代初和80年代初至90年代末梅雨的振荡较强。若从30年以上的尺度观察,20世纪50年代以后的梅雨振荡比50年代以前明显加强。

|
|
| 图 3. 长江中下游梅雨强度的能量密度 | |
在10年以下的时间尺度上,梅雨强度最强的年际尺度振荡出现在20世纪50年代,20年代和80年代也曾出现了较强的年际振荡。
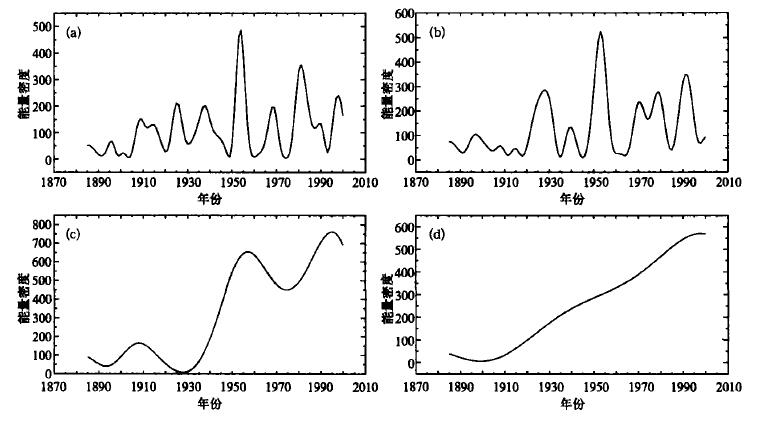
3.1 年际和年代际振荡能量密度的演变特征最大熵谱研究表明[6],长江中下游梅雨主要存在2~3年、6~7年、23~24年、36~37年的显著振荡周期。这里我们利用式 (6) 得到的上述4个尺度频率上的能量密度随时间的演变 (图 4),研究梅雨强度年际和年代际振荡随时间的变化。
|
|
| 图 4. 长江中下游梅雨强度不同尺度振荡的能量密度随时间演变 (a)2~3 a, (b)6~7 a, (c)23~24 a, (d)36~37 a | |
图 4是长江中下游梅雨强度振荡的能量密度随时间演变。由图 4a可以看到,梅雨强度2~3年尺度最强的振荡时段出现在20世纪50年代的前期,其次在20世纪80年代初也有较强的振荡,除此之外,在1995~2000年、1966~1970年、1934~1942年、1923~1928年、1907~1916年的2~3年振荡均表现得较强。由图 4b可以看出,长江中下游近100年来梅雨强度6~7年尺度的振荡在20世纪50年代初最强。另外,在20世纪20年代中后期、90年代初及70年代末80年代初3个时段6~7年尺度的振荡也比较强。如果从年代际的23~24年的尺度上来看 (图 4c),振荡的强弱基本是以20世纪40年代末50年代初为界划分的,在此之前,23~24年尺度的振荡很弱,其后时段振荡明显增强,其中20世纪90年代23~24年的振荡最强。若从更长的36~37年度上分析 (图 4d),梅雨强度变化呈现出随时间变化上升的趋势,即36~37年尺度的振荡在20世纪初以来呈现逐渐增强的趋势。
3.2 年际和年代际振荡的方差贡献随时间的变化我们用2~3年、6~7年频率的能量密度与1~10年总能量密度的比值代表这两个频率的振荡对年际振荡的方差贡献。用23~24年、36~37年频率的能量密度与11~40年总能量密度的比值代表这两个频率的振荡对年代际振荡的方差贡献。图 5为方差贡献随时间的演变,据此研究梅雨强度显著的年际和年代际振荡随时间的变化特征。
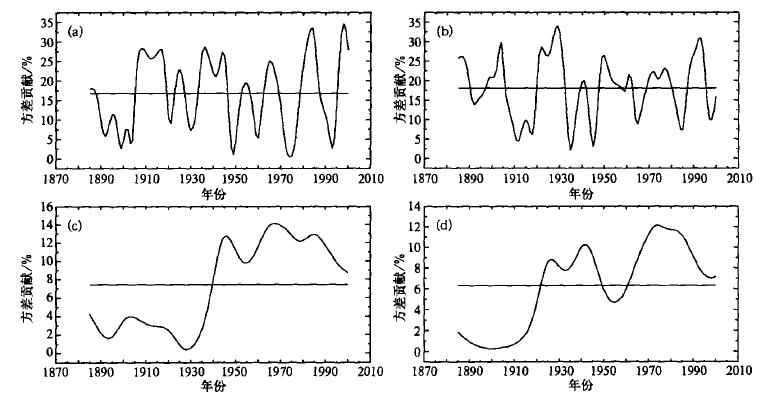
|
|
| 图 5. 长江中下游梅雨强度不同尺度振荡对年际和年代际振荡的方差贡献 (a)2~3 a, (b)6~7 a, (c)23~24 a, (d)36~37 a | |
从图 5a、b我们可以看出长江中下游梅雨强度的年际振荡有以下两个特点:① 2~3年和6~7年尺度的振荡对年际振荡有较大的方差贡献,特别是有些年份,这两个尺度的振荡对年际振荡的方差贡献在30 %以上,这从另一角度证明,长江中下游梅雨强度存在较显著的2~3年和6~7年年际振荡;②2~3年和6~7年尺度振荡的方差贡献的时间变化存在明显差异。由图 5a可以看出,近百年来,1978~1987年和1996~2000年两个时段的2~3年振荡的方差贡献最大。另外,1906~1918年、1934~1946年和1963~1969年的2~3年振荡的方差贡献也比较大。而图 5b显示,在1920~1932年较长时间段里,6~7年尺度的振荡方差贡献最大。其次在1898~1905年和1988~1995年6~7年尺度振荡的方差贡献也较大。由此可见,长江中下游梅雨强度的年际振荡在某一时段是以2~3年尺度振荡表现突出,而在另一时段是6~7年尺度的振荡表现明显。
由图 5c可以清楚地看出,在1939年以前长江中下游梅雨强度的23~24年尺度振荡对年代际振荡的方差贡献很小,23~24年尺度振荡对年代际振荡的方差贡献主要集中在1940年以后的时段。从36~37年尺度振荡对年代际振荡的方差贡献曲线图 (图 5(d)) 看出,在20世纪20年代以前,36~37年尺度振荡对年代际振荡的方差贡献最小,70年代以后36~37年尺度振荡对年代际振荡的方差贡献最大。另外,20年代初至40年代末这一时段的方差贡献也较显著,而50年代的方差贡献相对较弱。
4 结论与讨论(1) 本文提出用Morlet小波变换与统计检验相结合的方法,分析气候系统的多层次结构。结果表明,此方法有助于我们更清楚地了解近百年长江中下游梅雨的多尺度层次的谱系结构和演变过程。在60年的时间尺度上,1885~2000年的梅雨强度以1941年为界呈现强与弱两种状态。从40年的尺度观察,在梅雨较强的1941年以前阶段中,含有1885~1903年和1928~1941年两个梅雨相对弱的时段。而在梅雨较弱的1941年以后阶段中,含有1991~2000年梅雨较强的时段。从20年的尺度观察,梅雨强与弱阶段均含有更小尺度的相对强、弱时段。
(2) 从大的时间尺度而言,20世纪50年代以后梅雨强度的年际及年代际振荡均表现出增强趋势。20世纪50年代的前期和80年代初2~3年振荡较强,50年代初、20年代中后期、90年代初和70年代末80年代初6~7年振荡较强。50年代和90年代的23~24年振荡较强。
(3) 2~3年和6~7年振荡在梅雨强度的年际振荡中占30 %以上的方差贡献,但各个时段存在较大差异,1978~1987年和1996~2000年2~3年振荡对年际振荡贡献较大,而1920~1932年6~7年振荡对年际振荡贡献较大,23~24年和36~37年振荡的方差贡献在20世纪40年代以后非常突出。
本工作的意义在于,我们从不同时间尺度的层次角度来观察近百年长江中下游梅雨的突变,并对周期变化随时间的演变及其对年际振荡和年代际振荡的贡献进行了分析。从大的年代际尺度而言,20世纪40年代梅雨强度发生了突变,梅雨由较强趋势向较弱趋势转变,但是40年代以后的年代际振荡反而明显加强,说明近50~60年来梅雨变化具有明显的持续性特征。而从较小的年际尺度来讲,不同时段又存在较大差别。可见,长江中下游梅雨的异常变化是不同尺度振荡叠加和相互作用的结果,其成因涉及多种因素[12],我们将在以后的研究中就这方面做更深入地探讨。
| [1] | Allan R, Lindesay J, Parker D, El Nino Southern Oscillation and Climatic Variability. Victoria:CSIRO Publishing, 1996. |
| [2] | Reason C J C, Mulenga H, Relationships between south African rainfall and SST anomalies in the southwest Indian Ocean. Int J of Climatol, 1999, 19: 1651–1673. DOI:10.1002/(ISSN)1097-0088 |
| [3] | Gray W M, Atlantic seasonal hurricane frequency, Part I:El Nino and 30 mb quasi-biennial oscillation influences. Mon Wea Rev, 1984, 112: 1649–1667. DOI:10.1175/1520-0493(1984)112<1649:ASHFPI>2.0.CO;2 |
| [4] | Kuaff J A, The Modulation of Monsoon Intensity by Stratospheric QBO. Proceedings of the Seventeenth Annual Climate Diagnostic Workshop, 19-23 October, 1992: 306–311. |
| [5] | Schlesinger M, Ramankutty N, An oscillation in the global climate system of period 65-70 years. Nature, 1994, 367: 723–726. DOI:10.1038/367723a0 |
| [6] | 徐群, 杨义文, 杨秋明. 长江中下游116年梅雨 (一). 暴雨·灾害, 2001, 44: 44–53. |
| [7] | 徐群. 近46年江淮下游梅雨期的划分和演变特征. 气象科学, 1998, 18, (4): 315–328. |
| [8] | 魏凤英, 张京江. 近百年长江中下游梅雨变化的统计特征分析. 应用气象学报, 2004, 15, (3): 313–321. |
| [9] | Kumar P, Foufoula-Georgiou E, Wavwlet Analysis in Geophysics:An Introduction. In Wavelets in Geophysics. SanDiego: Academic Press, 1994: 1-43. |
| [10] | 刘太中, 荣平平, 刘式达, 等. 气候突变的子波分析. 地球物理学报, 1995, 38, (2): 158–162. |
| [11] | Jiang Jian Ming, Roy Mendelssohn, Franklin Schwing, et al. Coherency detection of multiscale abrupt changes in historic Nile flood levels. Geophys Res Lett, 2002, 29, (8): 112–1. |
| [12] | 李峰, 何立富. 长江中下游地区夏季旱涝年际、年代际变化的可能成因研究. 应用气象学报, 2002, 13, (6): 718–726. |
 2005, 16 (4): 492-499
2005, 16 (4): 492-499


