短期气候预测的主要对象是气温和降水的月、季平均量或总量。需要做预报是因为它们有年际变率,年际变率中有多大部分可以被预报出来显然是基本问题。由于起因和性质不同,月、季平均量的年际变率可以分成两部分:一部分是由缓慢变化的外部边界条件强迫产生的,例如,海表温度、海冰范围、土壤湿度、陆面温度等异常导致大气的月、季平均量异常,这些外部条件目前是气候预测的主要依据,所以无论从理论上还是实践上看,这部分年际变率被认为是可预报的或称潜在可预报的;另一部分变率是日际天气振荡产生的,强烈的大振幅天气振荡能在一定程度上影响月、季平均量及其年际变率。降水量尤其明显,有时一、两日的降水量能在月、季总量中占较大比例。天气振荡主要是由大气内部动力不稳定性产生的,缓变的外部条件在短时间内可以看作不变的,所以,Madden[1]把天气振荡产生的气候变率解释为“不变的气候”中的变率,称为自然变率。由于天气振荡的可预报时间上限只有两周左右,所以在气候预测的时效上,自然变率是不可预报的。潜在可预报和不可预报的变率还分别称为气候信号和气候噪声,两者之比给出分析对象的潜在可预报性度量。估计潜在可预报性主要有两个途径。一个是Madden[1~2]提出的低频白噪声延伸估计气候噪声的方法,Shulka[3]认为Madden的方法过高估计气候信号方差,过低估计潜在可预报性。Trenberth[4~6]指出Madden方法的应用中消除资料中的年循环的必要性以及估计自相关和独立取样时间的技巧。另一个途径是用方差分析法检验年际方差与季内方差之比的显著性[7~12]。其中文献[11~12]专用于分析降水量,它用一个逐日降水相关链过程估计降水量的季节内方差。这些方法有较多假设条件,结果对处理方法很敏感,例如Madden的方法来源于功率谱分析,只适用于平稳随机过程,对资料不做平稳化处理或处理方法不当都不能得到正确结果。在国内,吴洪宝[13]估计了青海省月平均气温的潜在可预报性。马开玉等[14],柳艳菊等[15]估计了我国年、月降水量的气候噪声。只估计出气候噪声而不跟气候信号方差做比较及统计检验实际上没有给出潜在可预报性的估计。潜在可预报性有地区、季节差异。本文用两个途径3个方法检验广西夏季降水量潜在可预报变率的显著性。
1 方法和资料 1.1 气候信号、气候噪声和信噪比估计估计气候噪声方差的低频白噪声延伸方法要求逐日资料序列满足平稳性,为此必须先消除原始序列中的年循环[1~6],本文采用文献[5]的方法移去了原始序列中的年循环。记消去了年循环后的夏季逐日降水量序列为xij,j=1,…,M,是年序号,i=1,…,N,是日序号,N=92。每年的季平均降水量为
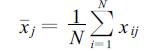
|
(1) |
式 (1) 中,xj的年际方差的无偏估计是
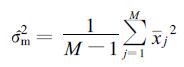
|
(2) |
式 (2) 中,σm2是总的年际变率,既包含气候信号,也包含气候噪声。
逐日序列的功率谱在频率为0至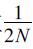
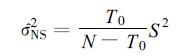
|
(3) |
式 (3) 中,S2是M年平均的季内方差,
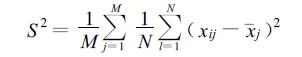
|
(4) |
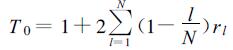
|
(5) |
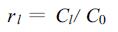
|
(6) |
式 (5) 和 (6) 中,Cl和rl分别是迟后l天的自协方差和自相关函数,也是多年的平均。其中,
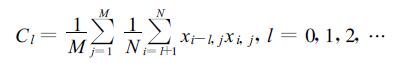
|
(7) |
T0的公式来源于功率谱与迟后自相关函数的关系式以及式 (7) 表示的Cl是有偏估计[4]。
检验是否存在潜在可预报信号的方法是建立原假设:没有信号。在原假设成立的情况下,比率
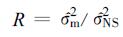
|
(8) |
服从分子自由度为M-1,分母自由度为M(Neff-1) 的F分布,Neff=N/ T0。T0为独立取样时间,Neff为有效长度。然后可根据假设检验的一般原理做出接受或拒绝原假设的结论。
1.2 方差分析途径
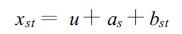
|
(9) |
式 (9) 中,s=1,…,M,是年序号,t=1,…,N,是季内日序号,u是总均值,as和bst是均值为零、方差为σa2和σb2的随机变量。是否存在可预报信号等价于检验原假设σa2=0,在逐日降水相互独立的情况下,可导出以下统计量
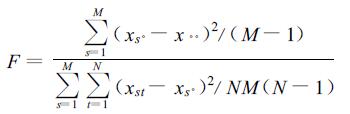
|
(10) |
式 (10) 中,
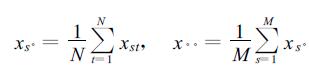
|
在原假设成立的条件下,这个比率服从分子自由度为M-1,分母自由度为M(N-1) 的F分布。式 (10) 的分子就是季平均降水量xs·的年际方差,它应该与按式 (2) 计算的xj的年际方差σm2相同,因为式 (2) 所采用的资料事先消去了年循环,已包含了式 (10) 中减总平均的运算。在逐日降水相互独立时,Cl=0,rl=0,由式 (5) 可知,此时T0=1。再由式 (3) 可见,式 (10) 的分母正是T0=1时的气候噪声方差。所以F的含义与R相同,也是总年际方差与气候噪声方差之比。但是,前一种方法要求资料先消去年循环,年循环分量是逐日变化的,所以两种方法计算的季内方差不等,况且前一种方法中rl ≠0,T0 ≠1,所以两种方法估计的气候噪声方差及R和F一般不相等,检验结果也会不同。另外应注意,式 (10) 分母中NM(N-1) 中的N不是分母自由度,它是在构成F分布随机变量时,利用了日降水量独立情况下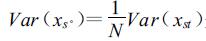
采用方差分析途径并且考虑日降水存在相关时,要检验σa2=0,是运用日降水的k天相关模型实现的[12]。把过程表示为{(xn,Jn):n=…,-1,0,1,… },其中xn是第n天的降水量,Jn表示在第n,n-1,…,n-k +1天的降水型,即第n及之前的k天各是雨日或无雨日的排列。如果第i天是雨日 (≥0.1 mm),记Hi=1,否则记Hi=0,则取
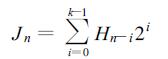
|
(11) |
{Jn}过程是状态为{0,1,…,2k-1}的马尔柯夫链。例如,如果k=2,则Jn能取值0,1,2,3共4个值,分别表示第n-1和第n天为:无雨日无雨日、无雨日雨日、雨日无雨日、雨日雨日4个状态。
记P=(pij) 为转移概率矩阵 (粗黑体表示向量或矩阵,下同),pij=P[Jn=j/Jn-1=i]。P的每行每列至多有2个非零元素,且每行之和等于1。记行向量π′=(π0,π1,…,πk-12) 是平稳概率向量,满足π′P=π′,且π′的元素之和等于1。给定{Jn}过程,{xn}过程是条件独立的,xn的概率分布只取决于Jn和Jn-1。xn的数学期望和方差为
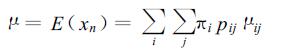
|
(12) |
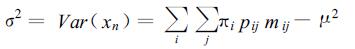
|
(13) |
式 (12),(13) 中,μij=E [xn/Jn-1=i,Jn=j],mij=E[xn2/Jn-1=i,Jn=j]。
记季降水总量为SN=x1 +x2 +… +xN,则当N足够大,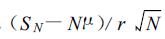
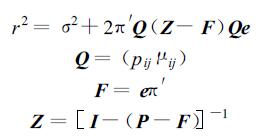
|
本文应用中取k=2,e是元素都为1的4行1列向量,I是单位矩阵。P、Q、F、Z、I都是4行4列矩阵。
因为xs·=SN/ N,故Var(xs·)=Var(SN)/ N2=r2/ N。所以,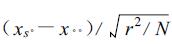
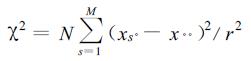
|
(14) |
因为x··是样本平均,失去一个自由度,所以自由度为M-1。给定置信水平α,当χ2>χα2时,拒绝σa2=0,认为有潜在可预报的年际变率。
1.3 资料广西区气象台提供的1980~2000年21年逐日降水量资料,夏季取6月1日至8月31日,全区取16个站,选站的原则是有代表性、基本上均匀分布、缺记录少的站。
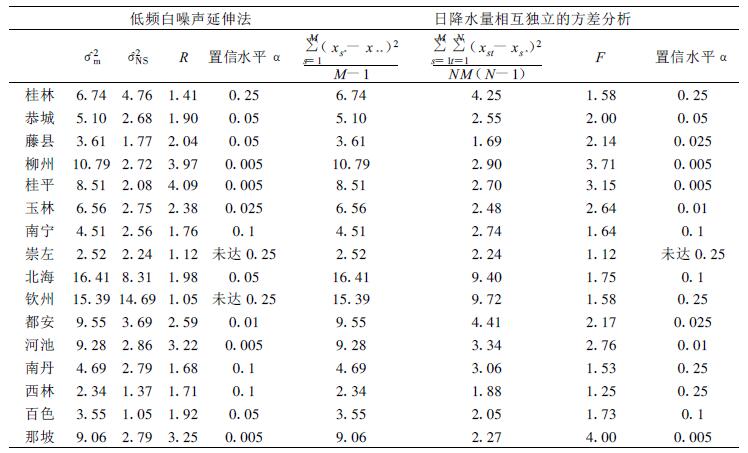
2 结果分析 2.1 低频白噪声延伸法和日降水量相互独立情况下方差分析的结果表 1列出这两种方法的主要结果及统计检验达到的置信水平α。关于置信水平,本文取M=21,N=92,统计量F和R的分母自由度分别等于和接近1911。在F分布临界值表中,分母自由度在120以上临界值变化已很小,所以本文F和R的分母自由度的差别已失去实际意义,按分母自由度∞查表。取α=0.25,0.1,0.05,0.025,0.01和0.005六个等级,对应的Fα是1.19,1.61,1.84,2.09,2.42和2.69。把计算得到的R和F值与Fα比较,得到对应的置信水平α。由表 1可见对所有站总的年际方差与气候噪声方差之比 (即R或F) 都大于1。如引言和方法所述,总的年际方差包含气候信号方差和气候噪声方差,含义是季平均量总的年际变化是由外源强迫和天气振荡两部分原因引起的。假设他们引起的变化相互独立,则总的年际方差等于气候信号方差与气候噪声方差之和。所有的站R和F大于1表明都有气候信号存在。比率大于2的站气候信号方差大于气候噪声方差,外源强迫引起的年际变率大于天气振荡引起的年际变率,用R和F来衡量分别有7个和8个站。考虑显著性,α≤0.05的站两种方法分别有10站和8站,说明对于多数站而言,存在可预报气候信号是可信的。两种方法的结果定性地相一致,置信水平最低 (α最大) 的是崇左站。置信水平高的是柳州、桂平、那坡站,两个方法的α都达0.005。
|
|
表 1 低频白噪声延伸法和日降水量相互独立的方差分析估计的气候噪声方差、信噪比和置信水平 |
2.2 日降水量相关情况下方差分析结果
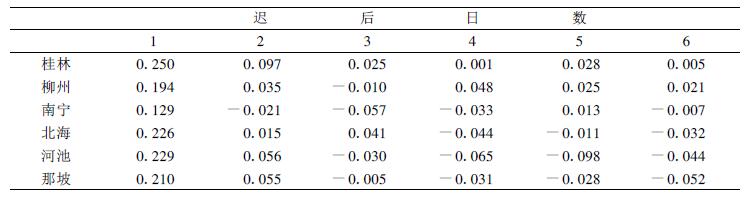
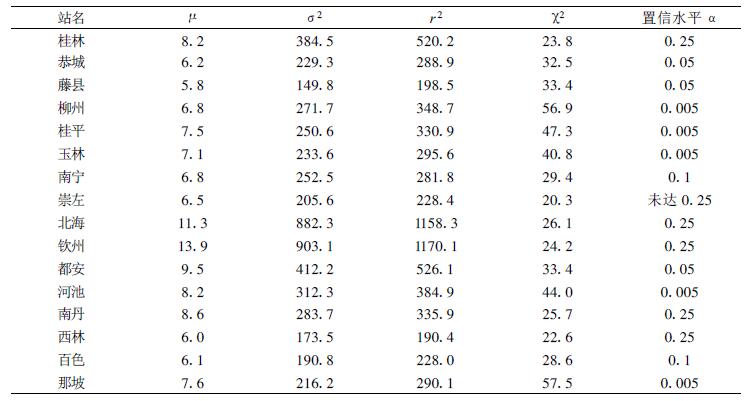
表 2是部分站的日降水量迟后相关系数,可见迟后相关系数衰减很快,所以与文献[11~12]一样取k=2,即用2天相关模型。表 3列出主要结果及达到的置信水平。同样取α=0.25,0.1,0.05,0.025,0.01和0.005,自由度M-1为20,χα2分别是23.6,28.4,31.4,34.2,37.6,40.0。从表 3可见,崇左站置信水平依旧未达0.25。α达0.005有柳州、桂平、玉林、河池、那坡5站,各站置信水平高低与前2个方法的结论基本一致。
|
|
表 2 日降水量的迟后相关系数 |
|
|
表 3 考虑日降水量相关的方差分析结果 |
综合表 1和3,全自治区大致可分成3片地理区域。在自治区中部和东部,包括河池、柳州、都安、恭城、藤县、桂平、玉林7站R平均值达2.51,表明气候信号方差大于噪声方差,3个方法的α都小于或等于0.05,是气候信号最强区域。南部包括崇左、钦州、北海、南宁4站R平均为1.48,气候信号方差只有气候噪声方差的一半左右,是气候信号弱的区域。北部和西部包括西林、百色、南丹、桂林4站R平均为1.68,气候信号强弱介于以上两地区之间。另外,那坡是位于西南角的气候信号强的单独一站。
气候噪声特别强的是钦州和北海2站,都位于沿海。由方法知,气候噪声强表示季内方差大,天气振荡强烈,从实际资料看正是如此,全区16站21个夏季共出现日降水量200 mm以上暴雨20次,其中8次在北海,6次在钦州,还各有一次达400 mm以上。显然,季降水量受强烈的天气振荡影响大的地区,短期气候预报难度大。
2.3 预报正确率上限估计讨论预报正确率一定要先规定一个预报质量评定标准。设预报量服从正态分布,我们取预报的绝对误差小于预报量年际均方差的0.68倍为预报正确的标准。这样,用气候平均作为预报值 (或预报距平是零) 可获得50 %的正确率。设预报量的变化是由信号和噪声两部分组成,且相互独立,预报正确率上限就是气候信号全部报出情况下的正确率,可导得预报正确率[13]
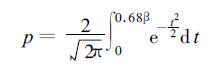
|
其中β是年际方差与气候噪声方差之比的均方根,即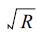
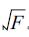
对广西夏季降水量的潜在可预报性用3种方法做统计检验得到如下结论:
(1) 全区各站都存在来源于外部强迫的气候信号,说明采用海温、海冰、土壤湿度、陆面温度等外部条件作为广西夏季降水的预报因子是合理的。
(2) 全区可分3个地理区域,中、东部气候信号最强,信号方差大于噪声方差。南部气候信号最弱,信号方差小于噪声方差。西部和北部气候信号强度介于以上两个地区之间。
(3) 以气候预报可获得50 %预报正确率作为评定标准,中、东部地区预报正确率上限约为72 %,南部约为59 %,西部和北部约为62 %。
应该指出,目前研究潜在可预报性所用的资料可以是观测资料或气候模式输出资料[7~9],但分析方法都依赖于统计。统计的结果受样本容量和样本随机性影响,只是对总体参数的一个估计,不能当确定性的结果看待。另外,方法中的假设对结果也有影响。方法假设外源强迫和天气振荡的作用是截然分开的,且相互独立,而实际上存在相关。方法还假设天气振荡对季平均量的作用是不可预报的,实际上,对于短期气候预报的时效而言,天气振荡的细节确实是不可预报的,但是它们对季平均量的总体效应可以采用统计方法考虑,这类似于大气环流研究中瞬变扰动对时间平均的物理量的输送作用。鉴于结果不可避免地受样本容量、样本随机性及方法假设条件影响,本文的结论或许是保守的,业务短期气候预测完全有可能超越这里估计的预报正确率上限。
| [1] | Madden R A, Estimate of the natural variability of time-averaged sea-level pressure. Mon Wea Rev, 1976, 104, (7): 942–951. DOI:10.1175/1520-0493(1976)104<0942:EOTNVO>2.0.CO;2 |
| [2] | Madden R A, A quantitative approach to long-range prediction. J Geo Res, 1981, 86, (c10): 9817–9825. DOI:10.1029/JC086iC10p09817 |
| [3] | Shukla J, Comments on "Natural variability and predictability". Mon Wea Rev, 1983, 111, (3): 581–585. DOI:10.1175/1520-0493(1983)111<0581:COVAP>2.0.CO;2 |
| [4] | Trenberth K E, Some effects of finite sample size and persistence on meteorological statistics. Part I:Autocorrelations. Mon Wea Rev, 1984, 112, (12): 2359–2368. DOI:10.1175/1520-0493(1984)112<2359:SEOFSS>2.0.CO;2 |
| [5] | Trenberth K E, Some effects of finite size and persistence on meteorological statistics. Part II:Potential predictability. Mon Wea Rev, 1984, 112, (12): 2369–2379. DOI:10.1175/1520-0493(1984)112<2369:SEOFSS>2.0.CO;2 |
| [6] | Trenberth K E, Signal versus noise in the southern oscillation. Mon Wea Rev, 1984, 112, (2): 326–332. DOI:10.1175/1520-0493(1984)112<0326:SVNITS>2.0.CO;2 |
| [7] | Zwiers F W, Interannual variability and predictability in an ensemble of AMIP climate simulations conducted with the CCC GCM2. Climate Dynamics, 1996, 12: 825–847. DOI:10.1007/s003820050146 |
| [8] | Zwiers F W, Kharin V V, Intercomparison of interannual variability and potential predictability:An AMIP diagnostic subproject. Climate Dynamics, 1998, 14: 517–528. DOI:10.1007/s003820050238 |
| [9] | Wang X L, Zwiers F W, Interannual variability of precipitation in a ensemble of AMIP climate simulations conducted with the CCC GCM2. J Climate, 1999, 12, (5): 1322–1335. DOI:10.1175/1520-0442(1999)012<1322:IVOPIA>2.0.CO;2 |
| [10] | Zheng Xiaogu, Nakamura H, Renwick J, Potential predictability of seasonal means based on monthly time series of meteorological variables. J Climate, 2000, 13, (7): 2591–2604. |
| [11] | Klugman M R, Evidence of climate change in United States seasonal precipitation data, 1948-1976. J Cli and Appl Met, 1983, 22, (8): 1367–1376. DOI:10.1175/1520-0450(1983)022<1367:EOCCIU>2.0.CO;2 |
| [12] | Klugman M R, A method for determining change in precipitation Data. J Appl Met, 1981, 20, (12): 1506–1509. DOI:10.1175/1520-0450(1981)020<1506:AMFDCI>2.0.CO;2 |
| [13] | 吴洪宝. 青海省月平均气温潜在长期可预报性估计. 南京气象学院学报, 1995, 18, (2): 282–287. |
| [14] | 马开玉, 董谢琼. 我国的降水资源及其稳定性与潜在可预报性. 气象科学, 1995, 15, (1): 72–79. |
| [15] | 柳艳菊, 马开玉, 林振山. 我国月降水量气候噪声的估计. 应用气象学报, 2000, 11, (2): 165–172. |
 2005, 16 (4): 445-452
2005, 16 (4): 445-452