GRAPES (Global and Regional Assimilation Prediction Enhanced System) 模式①标准初始化SI (Standard Initialization) 系统主要用于将分析场资料或粗网格模式资料处理成模式运行所必需的模式格点上的初始场及侧边界。由于数值预报是大气运动控制方程的初值问题, 初始场质量的好坏直接影响到模式的预报结果, 初始场的微小差别都可能导致截然不同的模式预报结果[1~4]。因此需要设计一个标准初始化系统, 它应尽可能精确地将所得到的各种信息加工处理成模式所必需的初始场, 并尽可能地反映真实大气的系统状况。由于每个模式都有其自身的特性, 不同的模式有不同的预报变量、不同的垂直坐标等, 所以必然需要适应模式特性的标准初始化系统。国外一些知名的数值预报模式如MM5 [5]、ARPS [6]都有其自身的标准初始化系统, 但大多数初始化系统采用的是比较简单的插值方案, 如水平方向采用双线性插值方案, 垂直方向采用高度线性插值或气压线性插值等; 美国最近发展的WRF [7]标准初始化方案也基本上沿用了MM5、ARPS的方案。GRAPES模式初始化系统在设计之初也尝试使用WRF SI方案, 但在某些天气个例中出现过模式积分不稳定现象, 因此有必要设计一个针对GRAPES模式的SI方案, 它能够通过较高精度的水平及垂直插值方法, 科学合理的物理方案设计来为GRAPES模式提供一个好的初始场。
① 陈德辉主持撰写.新一代多尺度数值预报系统(区域)技术手册(内部交流).
1 G RAPES模式的预报变量及垂直坐标 1.1 模式的预报变量GRAPES模式考虑到位温θ的保守属性, 以位温θ代替方程中的温度:
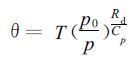
|
(1) |
同时引入气压Exner函数Π:
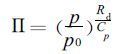
|
(2) |
其中, p0为1000 hPa, Rd为干空气比气体常数, Cp为干空气定压比热。静力平衡方程
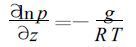
|
(3) |
改写为
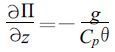
|
(4) |
为确保计算的稳定性, 提高计算精度, GRAPES引进“参考大气”基本状态。令Π、θ分别为参考大气基本状态廓线, Π′、θ′表示偏离参考大气状态的扰动量, 则:
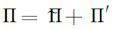
|
(5) |
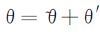
|
(6) |
这样GRAPES模式的预报变量就包括u、v、w、θ′、Π′、q共6个变量, 其中q可根据物理过程参数化的选择确定水物质的种类个数。
1.2 参考大气表达式GRAPES模式中假定参考大气为等温大气, 即: T=T0=常数。
根据静力方程 (3) 可得:
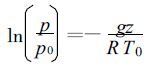
|
(7) |
由式 (1) 、(2) 及 (7) 可得:
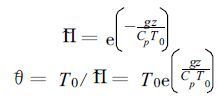
|
这样, 在大气温度为常数T=T0的假定下, 参考大气表达为
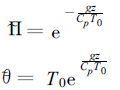
|
(8) |
绝大多数非静力模式通常假定参考大气满足静力平衡条件, 即:
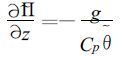
|
(9) |
用式 (4) -(9) , 则得到Π′和θ′满足的静力关系为:
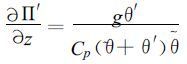
|
(10) |
GRAPES模式采用高度地形追随坐标:
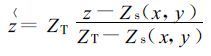
|
其中, Zs和Z
在模式坐标面参考大气表达式 (8) 及静力平衡关系式 (9) 、(10) 表示为:
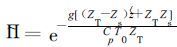
|
(11) |
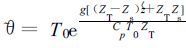
|
(12) |
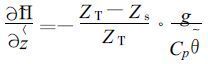
|
(13) |
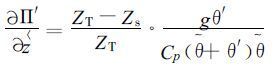
|
(14) |
GRAPES模式变量垂直方向采用Charney-Philips跳层分布, 图1给出了模式变量垂直分布图:
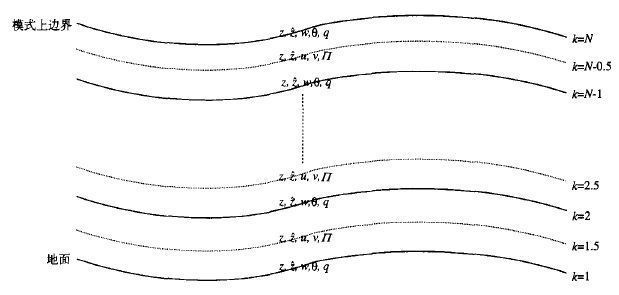
|
|
| 图 1. GRAPES模式变量垂直分布图 | |
2 GRAPES模式标准初始化系统结构及模式变量产生方案
图2给出了GRAPES模式标准初始化系统的结构图, 它通过3个主要模块完成其主要功能:静态资料准备、模式变量的水平插值及垂直插值。其中, 用户可选择粗网格模式产品以及GRAPES同化分析结果作为处理的初始资料, 水平插值和垂直插值有多种插值方案可供用户选择。
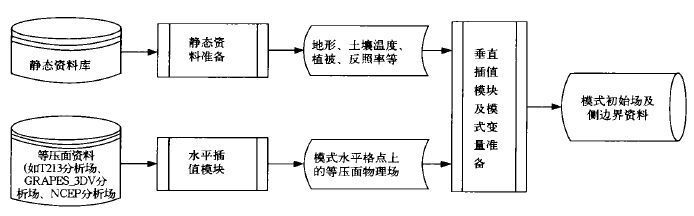
|
|
| 图 2. GRAPES模式标准初始化系统结构图 | |
2.1 静态资料准备
考虑到未来预报模式的需求, SI在设计上允许用户可任意控制其所需的预报区域。这主要通过控制文件中的空间参数 (起始经纬度、水平维数及水平分辨率) 来确定标准初始化的区域, 从高分辨率全球静态资料库中读出数据并根据需要进行水平插值、地形平滑等, 从而得到模式格点上的静态资料, 包括地形高度、经度、纬度、陆面参数、土壤类型、植被信息等等。其中用到的全球静态资料库中地形、土壤类型 (soil type)、土地利用 (land use) 的分辨率为30″, 植被分辨率为10′, 深层土壤温度分辨率为1°。由于静态资料只取决于空间参数而与时间参数无关, 所以这部分程序不需要每次都调用它。一旦确定了模式预报区域, 用户只需在第1次运行整个标准初始化程序时执行一次静态资料程序, 产生这个区域的静态资料, 在以后运行标准初始化程序时只需读入静态资料, 而不需再次执行静态资料程序, 从而使整个标准初始化程序能够高效运行。
2.2 水平插值和垂直插值水平插值模块用于将等压面的分析场资料或粗网格模式资料水平插值到GRAPES模式水平格点上。SI中提供了邻近格点的值、4点双线性插值以及16点插值3种插值方法可供选择。
垂直插值则将水平插值后的三维变量场垂直插值到GRAPES模式垂直坐标面上, 即将资料由等压面转换到高度面上。采用的垂直插值方法有简单高度线性插值、拉格朗日插值及三次样条插值3种方法可供选择。
2.3 模式变量产生方案由于GRAPES模式为非静力模式, 垂直速度作为其预报量之一, 为避免模式积分开始垂直速度增长太快, 造成模式运行不稳定, SI中假定初始时刻垂直速度为0, 即初始场温压场满足静力平衡关系。围绕此出发点, 我们在标准初始化系统中设计了如下3种模式变量产生方案:
(1) 方案一
①利用公式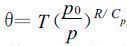
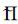
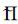
(2) 方案二
在具有收敛性及稳定性的插值函数中, 最常用和最重要的是样条插值函数, 它是一个整体上具有二阶连续微商的插值函数, 且由于用样条插值函数给出的插值曲线或曲面足够光滑, 运用时计算简单, 能满足一般实际问题的要求, 是数据逼近、数值微积分、微分方程数值解等计算数学领域中重要的工具[8]。在方案二及方案三中的垂直插值问题我们都选用的是样条插值方法。
①将等压面上的 (H, p)p垂直插值得到模式面上的 (p, pw)z〈, 采用三次样条垂直插值方法, 其中H表示高度场, pw表示模式半层气压。②将等压面上的 (T, u, v)p垂直插值得到 (T, u, v)z〈, 采用三次样条垂直插值方法; 将等压面上的 (q)p垂直插值得到 (q)z〈, 采用高度线性垂直插值方法。③利用式 (1) , 由 (T, p)z〈计算出 (θ)z〈。④利用静力平衡关系式 (4) , 从模式低层到高层垂直静力积分, 由 (θ)z〈求出模式面上的 (Π)z〈。⑤利用式 (6) , 由模式面的 (θ, θ)z〈求出模式面上的 (θ′)z〈, 其中, θ根据式 (12) 来计算。⑥利用静力平衡关系式 (13) , 从模式低层到高层垂直静力积分, 求出模式面上的 (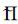
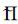
(3) 方案三
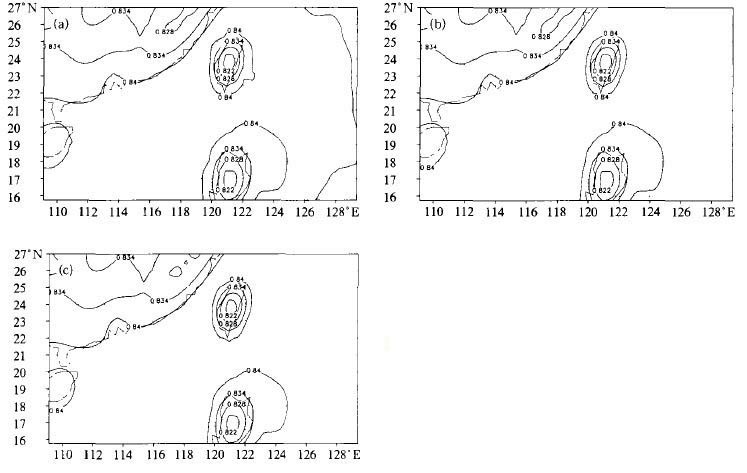
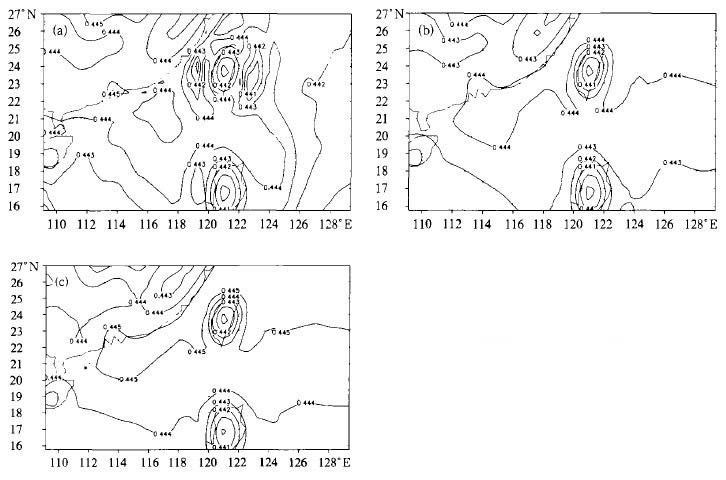
①将等压面上的 (H, p)p垂直插值得到模式面上的 (p, pw)z〈, 采用三次样条垂直插值方法, 其中H表示高度场, pw表示模式半层气压。接着利用公式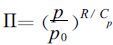
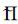
3种方案水平方向均采用双线性插值、模式水平分辨率均为60 km、相同的模式区域, 模式垂直方向采用等间距分层, 共为17层, 模式层顶为25000 m, 模式的背景场由国家气象中心中期预报模式T213的分析场提供。
总的来说, 3种方案计算出来的模式初始变量场u、v、q以及θ差别不是很明显 (图略), 变量场θ在个别层次差别有时能达到4 K, 但基本上系统结构的分布仍很相似, 只是中心强度有所不同。这说明变量场u、v、q以及θ对插值方法以及变量导出方案并不是很敏感。
但对于变量场Π, 情况则大不相同。图3及图4分别为3种方案产生的模式低层及模式高层初始Π场, 可以看出, 在模式低层 (大约5150 m), 3种方案产生的初始场没有很大的差别, Π场受地形的影响, 与地形结构非常相似, 尤其是方案二与方案三产生的初始Π, 差别非常细微, 方案一与另外两个方案的结果稍有差别, 这种差别完全是线性插值精度与三次样条插值精度的差别造成的; 而在模式高层 (大约20000 m), 方案一产生的初始Π与其余两种方案的差别很大, 方案一的结果明显很差, 在地形梯度较大的地方产生了很多虚假的扰动, 且在模式高层, 仍能很明显地看出地形的影响, 这样的初始场令人很难相信其正确性。而方案二、方案三的模式高层初始场Π看起来要好得多, 其结果只受地形的影响, 整场看起来非常平滑。总体来看, 方案三Π场值比方案二的值要大, 这是由方案本身的差别造成的。3种方案产生的不同结果可以解释为方案一、二的Π场是由θ通过静力平衡关系垂直积分得到, θ本身的插值误差就会垂直累积到Π场上, 越到高层, Π场的差别就会越大, 方案一采用的是最简单的线性垂直插值方案, 其误差也就最大, 于是到模式高层, 在地形梯度较大的地方, 就会有较大的误差积累, 从而造成虚假的扰动生成。
|
|
| 图 3. 标准初始化系统生成的模式第5层 (z〈=5147 m) 初始场Π场 (a) 方案一, (b) 方案二, (c) 方案三 | |
|
|
| 图 4. 标准初始化系统生成的模式第15层 (z〈=19853 m) 初始场Π场 (a) 方案一, (b) 方案二, (c) 方案三 | |
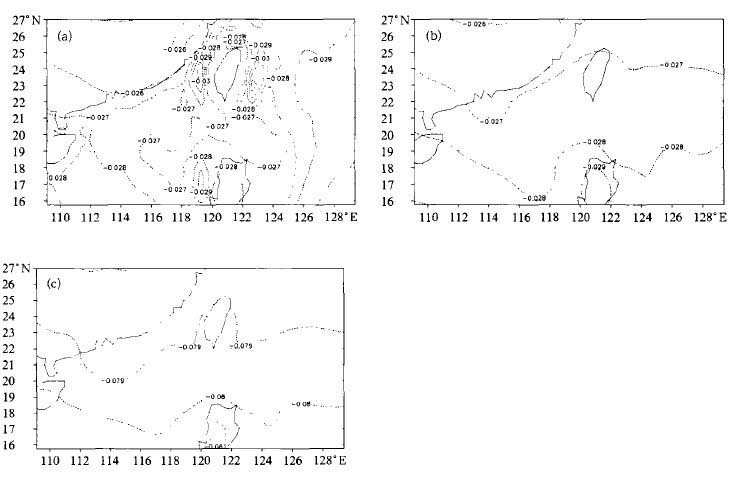
而对于模式的预报量Π′场, 如图5、图6, 3种方案产生的初始场的差别更为明显, 方案一的结果无论是在低层还是高层, 在地形梯度较大的地方都有许多虚假的扰动, 其效果明显不如方案二及方案三的结果; 方案二与方案三产生的模式初始Π′场间的差别也较Π场明显, 但由于这两种方案采用的是不同的参考廓线, 其值没有可比性。

|
|
| 图 5. 标准初始化系统生成的模式第5层 (z〈=5147 m) 初始场Π′场 (a) 方案一, (b) 方案二, (c) 方案三 | |
|
|
| 图 6. 标准初始化系统生成的模式第15层 (z〈=19853 m) 初始场Π′场 (a) 方案一, (b) 方案二, (c) 方案三 | |
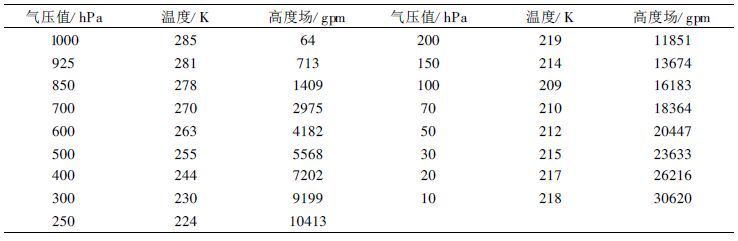
为能更清楚地看到各种方案产生的模式预报量Π′初始场, 我们设计了一个较为理想的状况, 即输入的背景场为水平均匀的温度场及高度场, 其值为粗网格模式资料全场水平平均值, 具体值对应表1。
|
|
表 1 理想状况下的温度场与高度场 |
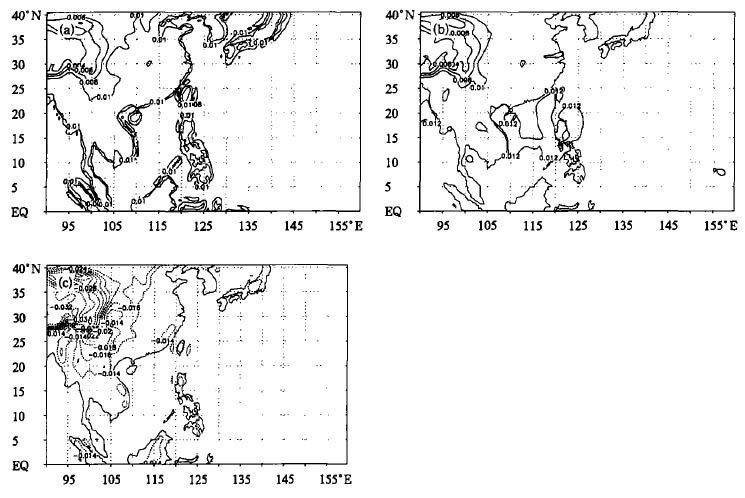
图7给出了理想状况下3种方案产生的模式预报量Π′初始场, 可以更明显地看出, 方案一产生的初始场有许多虚假的扰动, 整个场比较混乱, 难以反映背景场的形势, 而方案二及方案三整场看起来要平滑得多, 尤其方案三, 其整场结构与地形非常相似, 这与Π场特性是相吻合的。
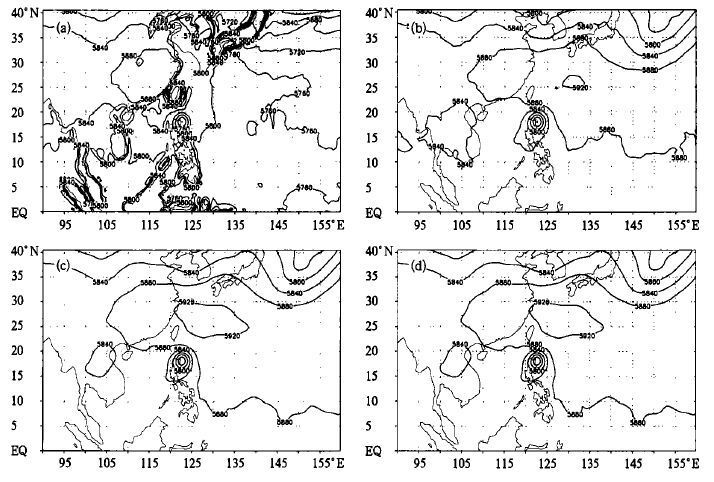
下面比较3种方案的结果与输入的等压面分析场之间的状况, 这里采用的等压面分析场是国家气象中心的中期预报模式———T213模式分析场。采用同样的后处理程序, 我们将3种方案产生的初始场还原到本来的T213等压面上, 与输入的背景场T213的分析场进行比较。从温度场的结果 (图略) 可以看出, 3种方案的结果都能较好地接近T213场, 其中尤以方案二的结果与T213场最为接近, 其误差不超过0.5 K, 方案一的误差主要来源于简单的垂直线性插值, 而方案三则可能来自于通过静力平衡关系内插得到θ而造成的。图8为500 hPa的高度场, 可以看出, 方案一的结果与原来的背景场相距甚远, 原来的系统已经完全看不见了, 若把初始场还原到等压面上的值与T213分析场的差作为插值误差, 则方案一500 hPa全场平均的误差绝对值为74.22 gpm, 这很容易让人怀疑结果的正确性, 从而影响对模式预报结果的可靠性; 而其余两种方案的结果与T213的分析场很相似, 尤其是方案三的结果, 几乎与原场一模一样, 其最大误差为0.8 gpm, 从500hPa全场平均的误差绝对值来看, 方案二为8.34 gpm, 而方案三只有0.13 g pm。根据方案设定, 我们认为方案一的误差有垂直插值方法带来的误差、通过静力平衡关系垂直积分得到Π造成的误差积累两种误差来源, 方案二的误差则主要来自于通过静力平衡关系垂直积分得到Π造成的误差积累。
|
|
| 图 7. 理想状况下标准初始化系统生成的模式第5层 (z〈=5147 m) 初始场Π′场 (a) 方案一, (b) 方案二, (c) 方案三 | |
|
|
| 图 8. 模式初始场还原到等压面500 hPa高度场 (单位:gpm) (a) 方案一, (b) 方案二, (c) 方案三, (d) T213分析场 | |
4 结论
GRAPES模式标准初始化程序在完成其主要功能的同时, 通过灵活的程序设计, 对初始化系统的时间、区域、分辨率、垂直层次、水平插值方法、垂直插值方法等都能灵活选取, 从而使得标准初始化系统可以很容易满足模式初值的各种需求, 在模式框架调试、与物理过程及三维变分 (3D-VAR) 系统的连接试验中提供了条件, 其方案也可以用于其他类似模式的初值生成中。通过3种模式初值生成方案的比较分析, 我们得到以下结论:
(1) 变量场u、v、T、θ对插值方法的精度并不是很敏感, 而高度场H以及Π场则对垂直插值方法的精度要求很高。
(2) 在3种模式变量产生方案中, 方案一的效果最差, 但它计算速度快, 在地形梯度不大的地方可以选择使用; 方案二与方案三的效果比较好, 用户可根据自己的需求任意选择。
致谢 GRAPES模式标准初始化系统方案设计得到中国科学院大气物理研究所的张道明、陈嘉宾老师的指导, 在此表示感谢。| [1] | Lorenz E N, Deterministic non-periodic flow. J Atmos Sci, 1963, 20: 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [2] | Lorenz E N, A study of the predictability of a 28-variable atmospheric model. Tellus, 1965, 17: 321–333. |
| [3] | Lorenz E N, The predictability of a flow which possesses many scales of motion. Tellus, 1969, 21: 289–307. |
| [4] | Lorenz E N. Effects of Analysis and Model Errors on Routine Weather Forecasts. Proc ECMWF Seminar on Ten Years of Medium-Range Weather Forecasting,ECMWF 1989. 115~128. |
| [5] | Jimy Dudhia, Dave Gill, Kevin Manning, et al. PSU/NCAR Mesoscale Modeling System Tutorial Class Notes and User's Guide. http://www.mmm.ucar.edu/mm5/documents/tutorial-v3-notes.html. |
| [6] | Xue Ming, Kelvin K Droegemeier, Vince Wong, et al. Advanced Regional Prediction System(ARPS) version 4.0 User's Guide. ftp://ftp.caps.ou.edu/pub /ARPS /ARPSdocs/ARPS4DOC.PDF. |
| [7] | User's Guide for Weather Research and Forecast(WRF) Modeling System Version 2. http://www.mmm.ucar.edu/wrf/users/docs/user_guide/contents.html. |
| [8] | 李庆扬, 关治, 白峰杉编著. 数值计算原理. , 2000. |
 2005, 16 (3): 374-384
2005, 16 (3): 374-384