我国是世界上受热带气旋影响最为严重的国家之一, 它们登陆时的狂风暴雨、巨浪和海水涌潮常常造成巨大的经济损失和人员伤亡。另外, 热带气旋还严重影响着远洋航行、海洋捕捞和近海养殖、石油和天然气的开采, 以及航天测控和军事活动等。热带气旋的影响和所造成的损失, 在很大程度上取决于其强度。关于西北太平洋上热带气旋的强度、中心位置等信息, 第二次世界大战后由美国关岛的飞机探测队探测获得, 1987年飞机探测停止后主要由卫星探测替代。1960年美国首颗极轨气象卫星成功发射后, Dvorak等[1~3]运用卫星云图 (可见光和红外云图) 上的热带气旋云型和云系特征研究热带气旋强度估计方法, 1975年基本成形; 随后增强显示红外云图投入业务应用, Dvorak又先后于1977、1984年两次改进和提高了热带气旋的强度估计方法。20世纪80年代末世界气象组织将Dvorak方法作为一种业务使用方法向全球推荐使用。在此之前, 我国也积极开展这方面研究, 如方宗义等[4]运用当时投入业务使用不久的日本静止气象卫星云图, 研究了西北太平洋热带气旋的强度估计方法; 江吉喜[5]研究了增强显示红外云图在台风分析中的应用, 其中一个重点就是简化Dvorak台风强度估计方法, 以适合预报员业务应用。
上述这些研究及所形成的方法, 在大洋上常规气象资料极其稀少的情况下, 对估计热带气旋强度起着十分重要的作用, 尤其是在1987年以后西北太平洋上停止了飞机侦察热带气旋业务之后更是如此。但上述方法是分析员根据自己的分析经验及对云型模式的认识来提取热带气旋的某些主要特征进行强度估计的, 客观性较差。比如, 用同一张卫星云图进行热带气旋强度估计, 不同人得到的结果很可能不一样, 有时甚至相差很大, 对此Kossin等[6]进行了较全面地分析研究。Engel [7]认为Dvorak方法的缺陷是分析员在使用该方法之前要进行较全面地分析技能训练, 而培养一个有经验的分析员则需要较长的时间和大量个例实践, 一旦分析人员工作变动或有新成员加入, 这种培训工作又要周而复始地进行, 这样不可避免地会浪费大量人力物力和时间。在这种情况下, 迫切需要开发一种客观的热带气旋强度估计方法。Zehr [8]运用美国静止气象卫星 (GOES) 的红外辐射亮温研究大西洋西部强热带风暴和飓风强度的客观估计方法, 得到了一些有意义的结果。随后, Velden等[9]开发了一种由静止气象卫星的数字红外云图客观估计热带气旋强度的方案, 并于2003年建立了强度估计模型。
本文根据国内外近十几年来的研究经验, 运用静止气象卫星红外展宽信息, 开发研究适用于西北太平洋上热带气旋强度的客观估计方法, 提高估计精度, 以供热带气旋分析预报使用。
1 资料和方法在卫星云图上, 发展成熟的热带气旋云系主要由3部分组成, 即无云或少云的眼区、眼区周围对流强盛的云墙以及外部的输入云带。热带气旋的强度主要由这3部分特征决定。Dvorak强度估计方法就是定性和部分定量地提取这些特征及其特征量的大小, 经过一系列的主观分析判断, 得到表征热带气旋强度的指数 (即“T指数”), 然后通过查算由历史资料统计分析制成的T指数与热带气旋中心气压对应表, 得到实时热带气旋中心气压和中心附近最大风力。静止气象卫星红外通道探测的辐射亮温 (TBB) 能够定量地展示热带气旋上述3部分特征, 从而使热带气旋强度的客观估计成为可能。
本文使用2001、2002年各年6月10日~8月10日共4个月高水平分辨率的TBB资料和在此期间出现的15个热带气旋, 研究热带气旋云系中各部分TBB值与热带气旋强度之间的定量关系。
TBB资料是由GMS-5红外一通道 (波长为10.5~11.5 μm) 探测到的红外展宽信息处理而成的[10], 其水平分辨率和时间分辨率分别是10 km和每小时1次, 覆盖范围为0°~60°N, 80°~160°E。热带气旋中心位置、强度等信息取自中国气象局主编的《热带气旋年鉴》。在上述的4个月中, 2001年有8个热带气旋:2号 (飞燕)、3号 (榴莲)、4号 (尤特)、5号 (潭美)、6号 (康妮)、7号 (玉兔)、8号 (桃芝)、9号 (万宜); 2002年有7个热带气旋:5号 (威马逊)、6号 (查特安)、7号 (夏浪)、8号 (娜基莉)、9号 (风神)、11号 (凤凰)、12号 (北冕)。当热带气旋中心附近最大风力≥8级 (17.2 m/s)(即热带风暴) 时, 作为入选条件。选用热带气旋中心最低海平面气压作为定量强度估计的标准, 风力作为选取样本的先决条件。按此规定, 在上述时段内, 所获TBB资料与热带气旋年鉴中6 h间隔的台风中心位置资料相匹配的样本数共有261个, 其中2001年133个, 2002年128个。
在选取热带气旋云系中与其强度相关的TBB因子时, 采用以热带气旋中心为圆心, 在其半径为150 km范围内以10 km为间隔划分同心圆环, 所选的TBB因子包括:以热带气旋中心40 km范围内最暖像元的TBB值作为其中心区温度, 距中心20~150 km环面上所有格点TBB的平均值代表中心区周围对流云强度, 同时还考虑了各个环带上的平均TBB值、最暖和最冷TBB值, 以及中心区最暖TBB值与各环带平均TBB值之差, 与各环带内最暖、最冷TBB值之差。
运用统计回归方法, 计算这些因子与热带气旋中心气压之间的关系, 求取强度估计算式。考虑到热带气旋云型演变的非连续性和每个时刻卫星观测的瞬间性, 对计算出的各个时次中心气压作不同时间尺度的加权滑动平均, 求得最终热带气旋中心气压, 研制完整的热带气旋中心强度计算流程。同时, 还运用2000年4号、8号台风对所得到的算法作检验, 分析讨论其可用性。
2 强度算式和结果分析 2.1 热带气旋强度估计算式及计算流程对上述所有TBB因子作置信区间为95%的逐步回归, 并加入热带气旋中心所在位置的纬度因子, 经过多次试验和因子筛选, 得到一个最优的多元线性回归式:
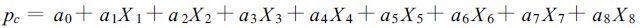
|
(1) |
其中:pc为估计的中心气压, 单位:hPa; X1是第4环带上的平均温度; X2是第12环带上的平均温度; X3是第15环带上的平均温度; X4是第3环带上的最暖温度; X5是第3环带到第13环带上的最暖温度; X6是中心区温度与第9环带上最暖温度之差; X7是中心区温度与第3环带到第9环带上的最暖温度之差; X8是热带气旋中心所在的纬度; 式中第4环带指距热带气旋中心30 km到40 km的圆形环带, 其他以此类推。
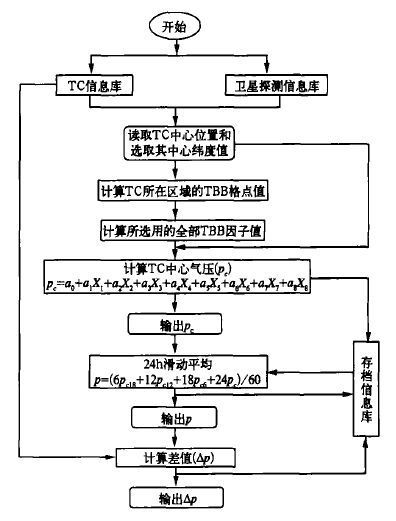
系数a0, …, a8(未经过标准化) 是由2001、2002年两年15个热带气旋261个样本进行逐步回归计算后得到的, 其中:a0=1020.775, a1=0.489, a2=-0.543, a3=0.688, a4=-0.295, a5=0.131, a6=0.414, a7=-0.425, a8=-0.802。由此构建一个强度估计流程, 如图1所示, 其中包括由上述式 (1) 计算得到的热带气旋中心气压pc和经过时间加权滑动平均后求出的最终气压p, 以及与中央气象台实时发布的气压值作比较, 得到的计算差值Δp。
|
|
| 图 1. 热带气旋强度客观估计流程图 | |
2.2 强度估计算式和流程的建立及误差分析 2.2.1 热带气旋云系特征因子的选取
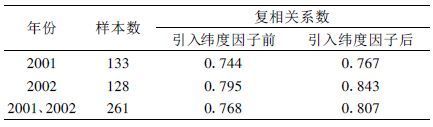
热带气旋中心强度主要由热带气旋云系特征决定, 而GMS-5红外通道的TBB值能够定量地反映出云和云系的各种变化。因此, 对2001年、2002年全部15个个例中相关的TBB因子分别作统计回归计算, 同时对这261个样本作类似的综合计算, 得到置信区间为95%时各自的复相关系数 (表1), 其值分别为0.744、0.795、0.768, 按统计学观点, 这些值所反映的相关性并不很好。
|
|
表 1 热带气旋强度因子与其强度多元回归复相关系数表 |
2.2.2 引入纬度因子的试验及误差分析
热带气旋中心所在纬度可能会对其强度产生一定的影响, 比如随着纬度的增加对流层层顶高度逐渐降低, 相应地对流层层顶温度逐渐上升, 从而影响热带气旋眼墙处的对流强度, 使得眼墙上空云顶温度的最低值随着纬度的增加而增高, 进而影响到热带气旋的强度。另外, 随着纬度增加, 海表温度逐渐降低, 也会影响到热带气旋中对流云的发展强度。因此, 将热带气旋中心所在处的纬度作为一个因子引入回归算式中, 重新计算。实验结果表明, 其复相关系数出现明显提高 (表1), 如2001年的复相关系数从0.744提高到0.767, 2002年从0.795提高到0.843, 2001、2002年总平均从0.768提高到0.807, 提高了0.039。
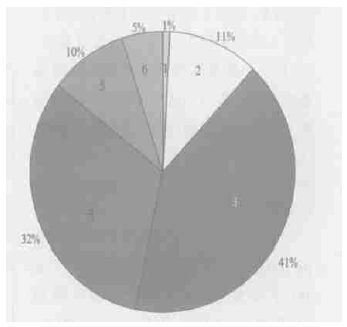
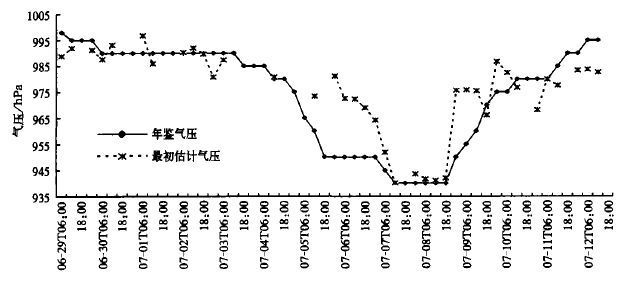
引入热带气旋中心纬度因子后, 对上述261个样本作回归计算, 其结果的误差分布如图2所示, 误差主要分布在3、4两区, 即气压差在±10 hPa之内的占整个样本数的73%。说明估计气压与年鉴气压的差别不是很大, 具有一定的可信度。这里以整个261个样本中误差最大的2002年6号台风为例作简单分析, 其中最大误差为-31.17 hPa (图3)。分析发现, 该台风的生命史从6月29日开始至7月12日结束共14 d, 在7月4日1 8 :0 0(世界时, 下同) 到7月5日18 :00的24 h内台风急剧加强, 气压从980 hPa下降到950 hPa, 下降了30 hPa, 而我们利用回归方程计算得到的估计气压显然没有捕捉到该台风强度的这种迅速加强, 估计值出现了较为严重的滞后现象; 同样在7月8日18 :00到7月9日18 :00的24 h内该台风又迅速减弱, 气压从940 hPa迅速上升至970 hPa, 而式 (1) 同样也没估计出这种变化。因此, 可以说对于估计这种快速加强或快速减弱的台风强度, 我们得到的回归式还有一定的局限性, 有待于加入更多情况复杂、强度突变的台风进行更深入的研究。另外, 由于GMS-5超期工作多年, 在7月3日12 :00到7月5日18 :00期间卫星扫描丢线 (缺测) 过多, 缺少相匹配的实时TBB资料, 也是引起误差较大的一个重要原因。同时当台风急剧变化时, 会加大精确定位中心的难度, 这也会影响到最终的估计结果。但从图中同样可以看到, 在6号台风发展的初始阶段、成熟阶段以及后期消亡阶段, 由回归算式得到的强度与年鉴气压十分接近, 两条曲线近乎重合, 估计效果十分好。
|
|
| 图 2. 估计气压与年鉴气压之差在各等级中占样本总数的百分比分布 (1表示Δp≤-20 hPa, 2表示-20 hPa<Δp≤-10 hPa, 3表示-10 hPa <Δp≤0 hPa, 4表示0 h Pa<Δp≤10 hPa, 5表示10 hPa <Δp≤20 hPa, 6表示Δp >20 hPa。正值 (负值) 表示估计气压相对于年鉴气压的低估 (高估)) | |
|
|
| 图 3. 2002年6号台风各时次中心估计气压与年鉴气压曲线 | |
2.2.3 时间滑动平均试验及其误差分析
卫星云图分析指出, 热带气旋云型演变常常不是一个连续过程, 在短时间内往往发生很大变化, 尤其是用时间间隔较短的数字图像进行强度估计时, 这种变化更为明显。其原因主要是由于对流活动的短周期变化、日变化以及周围环境场更长周期的扰动对热带气旋云系共同作用的结果, 从而造成某些时次强度估计值的虚假增大或减小。采用时间滑动平均方法滤掉短期内强对流不稳定因素对热带气旋云型的干扰, 可以减小这种误差, 使强度估计结果更为精确。实验表明[3], 运用时间滑动平均后拟合的气压强度变化曲线比用单个时次卫星资料获取的强度估计曲线更接近热带气旋实际的强度变化, 并且利用滑动平均方法除了可以平滑掉短期内不稳定因素造成的云特征波动外, 还有利于改进那些云型变化大大超前于地面气压场变化的气旋强度估计结果。
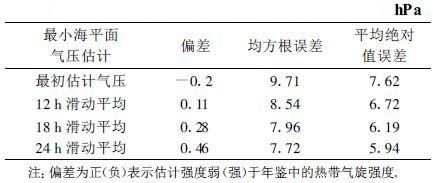
为了得到最优的时间间隔, 从当前时刻开始对最初估计气压分别作过去12、18和24 h不同时间权重的滑动平均。如进行24 h滑动平均, 是用当前时刻的气压值和过去24 h内得到的所有气压值做不同权重的线性滑动平均。由于本研究采用资料的时间间隔为6 h 1次, 故24 h滑动平均算式即为当前时刻的估计气压乘以24, 过去6 h的估计气压乘以18, 过去12 h的估计气压乘以12, 过去18 h的估计气压乘以6, 然后将所有为经过24 h得到的值相加求平均, 最后的结果即滑动平均后的气压值。在对这261个样本作这3种滑动平均后, 再分别计算它们的偏差、均方根误差及平均绝对误差 (表2)。
|
|
表 2 不同时间滑动平均前后各项误差比较 |
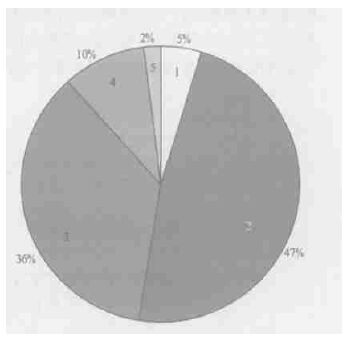
由表2可见, 经时间滑动平均后, 最初估计气压与年鉴气压之间的差别减小, 各项误差有了不同程度的降低。均方根误差经过24 h滑动平均后达到最小, 说明对西北太平洋热带气旋进行24 h的滑动平均在所有的时间间隔中最优。同时对经过24 h滑动平均后各种不同等级的误差作再分析 (图4), 发现经过24 h滑动平均后, 估计气压和年鉴气压之差有83%(2区和3区之和) 落在±10 hPa之间, 比原来的73%提高了10%, 表明与年鉴气压更加接近。
|
|
| 图 4. 估计气压经24 h滑动平均后与年鉴气压之差在各个等级中占样本总数的百分比 (1表示-20 hPa<Δp≤-10 hPa, 2表示-10 hPa <Δp≤0 hPa, 3表示0 hPa<Δp≤10 hPa, 4表示10 hPa<Δp≤20 hPa, 5表示Δp >20 hPa。正值 (负值) 表示估计气压相对于年鉴气压的低估 (高估)) | |
此外, 从表3中可以看出, 经过滑动平均后, 最初估计气压与年鉴气压的相关性大大提高, 24 h滑动平均结果与年鉴气压的相关系数达到0.89。与美国近期的研究结果十分接近, 甚至优于他们的结果。而在上节中提到的2002年6号台风经过不同时间的滑动平均后, 误差也有不同程度的减小, 但其最优的时间滑动平均不是24 h, 而是18 h (表略)。这与Velden等人[9]得到的对于强度变化迅速的热带气旋其滑动平均的时间间隔要相应减小一些的结论一致。
由于本研究受《热带气旋年鉴》资料的限制, 所用资料间隔为6 h 1次, 而在实际应用中可以使用1 h间隔的红外资料, 这可能会使最优滑动平均的时间间隔相应减小, 准确率也可能会得到相应的提高。
|
|
表 3 估计气压经滑动平均前后与年鉴气压的相关系数 |
2.3 滑动平均后的个例分析
由以上分析可知, 式 (1) 计算出的热带气旋中心气压经过滑动平均后, 整体而言准确率有明显提高。但是, 并非所有个例都如此, 下面举出正、反两方面的例子作简单分析。
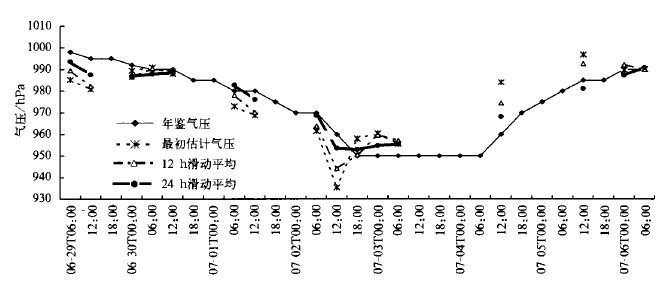
2002年5号台风 (威马逊) 是一个较好的例子 (图5)。原始估计强度随时间变化起伏较大 (细虚线), 最大强度出现高估, 且出现时间比实际最大强度的出现时间提前, 这与卫星观测的云型变化超前于地面气压场变化相吻合。经滑动平均后, 各项误差显著降低 (见表4), 气压随时间的变化曲线与年鉴气压更加接近, 强度估计结果更精确, 尤其是24 h滑动平均的结果与实际台风强度十分相近, 并捕捉到了它的快速加强及随后的强度减弱, 整体误差十分小; 同时也可以看出经过24 h滑动平均后的估计气压在台风前期发展到热带风暴阶段比年鉴中的气压略低, 而在后期强度维持少变阶段估计气压又略高于年鉴气压, 但是这种高低误差不超过5 hPa, 估计效果非常好。
|
|
| 图 5. 2002年5号台风中心滑动平均前后的估计气压与年鉴气压时间变化曲线 | |
|
|
表 4 2002年5号台风估计气压经滑动平均前后各项误差比较 |
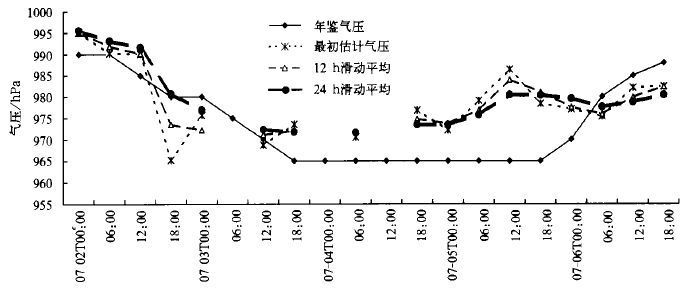
2001年4号台风 (尤特) 是一个较差的例子, 由式 (1) 计算出的最初估计气压在其整个生命史大部分时间都出现不同程度的低估 (图6), 经滑动平均后, 估计结果虽有一定提高, 但误差改善并不明显 (见表5), 经过24 h滑动平均后最大误差仍为15 hPa左右, 且误差主要出现在强度稳定少变阶段。反查GMS-5红外云图, 发现该台风生命史中大部分时间内螺旋云带结构极不对称, 而上述回归算式中所选因子是按常见热带气旋云系挑选并计算的, 这可能是导致估计误差增大的一个方面。另一方面, 不对称的螺旋结构会加大利用卫星进行热带气旋中心定位的难度, 导致热带气旋中心周围TBB因子计算不准确, 影响强度估计精度。解决这个问题的有效途径是在气象卫星不断发展的基础上, 获取高精度热带气旋中心定位信息, 包括中心密闭云区和风垂直切变环境场中的云型定位, 同时进一步扩大热带气旋样本数, 优化入选方程的因子, 使其适用于各种热带气旋云型变化, 提高估计精度。
|
|
| 图 6. 2001年4号台风中心滑动平均前后的估计气压与年鉴气压时间变化曲线图 | |
|
|
表 5 2001年4号台风估计气压经滑动平均前后各项误差比较 |
3 检验
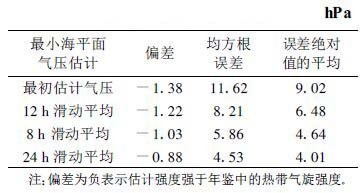
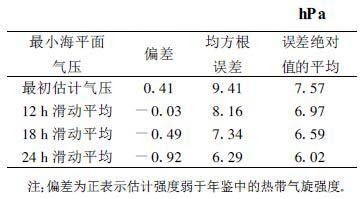
为了验证上面所得算法的可信度, 在力所能及获取的原始存档卫星资料及加算出的TBB资料中, 随机选取2000年4号和8号两个台风作检验, 并进行误差分析。首先按上述相同方法, 将热带气旋风速≥18 m/s时作为入选条件。计算结果如表6所示, 8号台风 (杰拉华) 经24 h滑动平均后均方根误差降到6.29 hPa, 误差绝对值平均降到6.02 hPa, 均小于10 hPa; 与表2比较, 前者减小了1.43 hPa, 后者仅增大了0.08 hPa。误差主要出现在强度稳定少变阶段, 而在其减弱消亡阶段, 最初估计气压与年鉴气压比较接近, 估计效果很好。
|
|
表 6 2000年8号台风估计气压经滑动平均前后各项误差比较 |
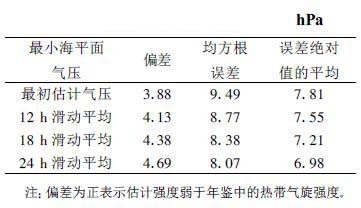
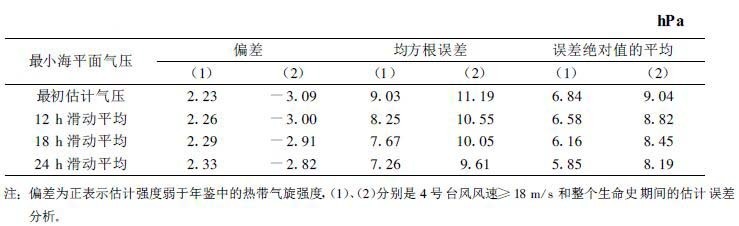
用式 (1) 计算4号台风 (启德) 整个生命史的强度, 并作相应的误差分析。4号台风从7月2日12 :00开始编报到7月11日12 :00消亡, 整个生命史共有32个时次资料, 其中风速<18 m/s的有11个时次。表7列出了4号台风风速≥18 m/s和整个生命史中的各项误差, 可以看出4号台风在风暴以上强度阶段的估计结果优于表2中的相应项, 并且在包括其前期低压阶段的计算结果中, 其均方根误差和误差绝对值的平均虽然有不同程度的增大, 但依然在10 hPa之内, 表明上述强度计算式也适用于热带低气压的强度计算。误差增大的原因可能是4号台风生命史初期的近3 d中 (11个时次) 强度变化缓慢, 风速较稳定地维持在15 m/s, 而式 (1) 主要是由风速≥18 m/s热带风暴以上强度的样本经过统计回归后得到的。
|
|
表 7 2000年4号台风估计气压经滑动平均前后各项误差比较 |
用式 (1) 估计的强度, 在风暴逐渐加强的初始阶段和后期强度逐渐减弱阶段效果很好, 误差较小; 在风暴发展最旺盛阶段没能很好地估计出强度, 误差较大, 但仅有少数时次 (共4个时次) 强度估计误差超过10 hPa, 大部分时次估计气压与年鉴气压之差都在10 hPa之内。
4 结语运用卫星探测信息客观地估计热带气旋的强度, 是热带气旋业务分析预报中的一项急需工作。本研究的结果显示出该方法可望应用在业务上, 对热带气旋的数值预报和日常业务分析预报有重要帮助。
目前出现的误差, 原因是多方面的。首先我们将《热带气旋年鉴》的气压值作为标准值, 而某些时候并不完全正确, 比如同一个热带气旋同一时刻的值, 有的就与日本、美国关岛报告的不一样。其次, 由于受已有TBB资料时段的限制, 我们在建立回归计算式时热带气旋样本数还不足够多, 以至于一些较特殊的热带气旋云型的特征因子没能提炼出来, 造成回归算式概括率和代表性不完善, 对于某些强度快速变化的热带气旋不能很好地进行估计。另外, 由于GMS-5超期工作, 卫星扫描丢线过多, 导致热带气旋生命史中一些时刻的TBB资料缺乏和质量受影响。
针对这些问题, 下一步将继续扩大热带气旋样本数, 并运用每3 h时间间隔的TBB资料, 综合参照我国、日本、美国关岛3家的气压资料, 挑选最优因子和计算最佳系数, 建立适合业务应用的算式。一旦计算出热带气旋中心气压, 利用过去已有的气压与风力的统计关系和有关算式, 可以立即查算出中心附近最大风力, 从而构成一个完整的热带气旋强度客观估计业务技术。
| [1] | Dvorak V, Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon Wea Rev, 1975, 103, (5): 420–430. DOI:10.1175/1520-0493(1975)103<0420:TCIAAF>2.0.CO;2 |
| [2] | Dvorak V, Wright S, Tropical Cyclone Intensity Analysis using Enhanced Infrared Satellite Data. Proceedings of the 11th Technical Confefence on Hurricanes and Tropical Meteorology, AMS, 1977, 268. |
| [3] | Dvorak V. Tropical Cyclone Intensity Analysis using Satellite Data. NOAA Tech Rep NESDIS 11, 1984 ,1~47. [Available from NOAA/NESDIS, 5200 Auth Rd, Washington, DC 20233]. |
| [4] | 方宗义, 周连翔. 用地球同步气象卫星红外云图估计热带气旋强度. 气象学报, 1980, 38, (2): 150–159. |
| [5] | 江吉喜. 增强显示红外卫星云图在热带气旋分析中的应用. 气象学报, 1986, 44, (4): 482–487. |
| [6] | Kossin J P, Velden C S, A pronounced bias in tropical cyclone intensity estimation based on the Dvorak technique. Mon Wea Rev, 2004, 132, (1): 165–173. DOI:10.1175/1520-0493(2004)132<0165:APBITC>2.0.CO;2 |
| [7] | Engel G T. Satellite Applications at the Joint Typhoon Warning Center. Rapporteur Report, Topic 0.le, 5th WMO International Workshop on Tropical Cyclones, Tech Doc WMO/TD No1136. Geneva:WMO, 2002. |
| [8] | Zehr R, Improving Objective Satellite Estimates of Tropical Cyclone Intensity. Extended Abstracts, 18th Conf on Hurricanes and Tropical Meteorology, San Diego, CA, AMS, 1989: J25–J28. |
| [9] | Velden C S, Olander T L, Zehr R, Development of an objective scheme to estimate tropical cyclone intensity from digital geostationary satellite infrared imagery. Wea Forecasting, 1998, 13: 172–186. DOI:10.1175/1520-0434(1998)013<0172:DOAOST>2.0.CO;2 |
| [10] | 朱小祥. 气象卫星辐射亮温产品.气象卫星业务产品使用手册. 北京: 气象出版社, 1999: 187-198. |
 2005, 16 (3): 283-292
2005, 16 (3): 283-292