当前大气边界层湍流输送的基础———局地理论正面临着非局地理论的挑战。在局地湍流输送的理论基础上建立的许多用于各种尺度数值预报模式的边界层参数化方案 (空气动力学方案, 高分辨率方案等) 由于计算方便, 而且在许多典型的情形下计算结果合理, 从而得到了广泛的使用。然而许多研究工作[1~3]指出:在大气边界层内的动量与质量的传输并不仅仅取决于局地性质, 而且与边界层结构、大涡的活动有紧密的关系。例如我们不能期望用局地理论能处理已经发展完善的混合层内动量与质量的输送问题, 也无法使用它去解释一些逆梯度输送的现象[2, 4~6]。为此, 历史上也曾发展过一些高技巧的物理参数化方法来解决上述的问题, 如Mellor等[7]提出了高阶闭合方案。Benoit等[8]和Pan等[9]使用了1.5阶及更高的湍流高阶闭合方案进行预报试验。这些试验表明高阶闭合能够描述混合得很充分的边界层, 但是Hong等[10]指出, 严格地说高阶闭合仍然是在局地理论的基础上建立的, 在有强顶盖逆温出现时, 它的表现并不使人满意。
为了解决上述问题, 非局地理论逐渐发展起来, 如非局地K理论 (non-local-K theory) 和穿越理论 (transilient theory)[11~12]。非局地K理论建筑在Deardorff [4], Troen等[5], Holt slag等[2, 13]的工作基础上, 它对预报变量 (C, u, v, θ, q) 的扩散方程为:
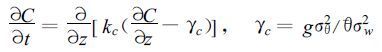
|
(1) |
其中涡旋交换系数kc及局地梯度的订正函数γc是需要进一步由参数化方法决定的量。如果将位温与垂直速度脉动量看成是由大涡造成的, 那么该式就是非局地K理论的基础方程。由该方程可知, 在高度z上预报变量C
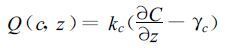
|
(2) |
当然, 这个等式两端都是时间的函数。Troen等[5], Holtslag等[13~14]曾将此方程用于混合层的大气扩散问题。Hong等[10]也将此方程用于中期数值预报模式中。
Stull [11]发展的穿越理论也属于湍流输送的非局地理论, 该理论完全脱离了K理论的束缚, 用湍流区域a、b之间的被预报量空间差值的积分来表达其时变速率。
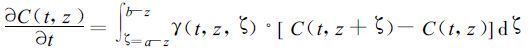
|
(3) |
假设在湍流区外的湍流通量为零, 即Q (c, z=a)=0, 那么在高度z=z1处, t时刻的湍流通量Q (c, z=z1) 为
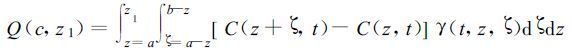
|
(4) |
由式 (4) 可见, 在湍流穿越理论中, 湍流通量是用整个湍流区的平均量的分布与穿越积分核函数来确定的, 而穿越积分核函数是由当地的梯度与湍流交换系数来确定的, 这与传统的局地梯度理论有着实质性差别。
在局地理论发展的几十年时间里, 如何通过外边界条件和平均要素及其导数来确定局地湍流交换系数是研究工作的重点。同样在非局地理论中, 如何确定相应的参数如式 (1) 中的涡旋交换系数kc、订正函数γc和式 (4) 中的穿越积分核函数也必然是研究工作的核心所在。徐大海[15~17]推导出了与式 (1) 形式相同的局地通量计算式, 同时也推导出了式中涡旋交换系数kc及订正函数γc与局地湍流统计量之间的一些理论关系, 该研究还给出了多尺度湍流的通量相加关系。本文研究重点就是在上述研究基础上, 发展出湍流通量的非局地多尺度湍流计算方法, 之后采用青藏高原昌都的观测试验数据进行计算, 并与局地相似理论的计算结果进行了对比分析。
1 湍流通量的非局地多尺度湍流理论计算方法的建立将任一气象要素c分解如下[17]:
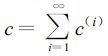
|
(5) |
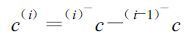
|
(6) |
其中c(i) 为第i级脉动值, (i)-c表示c的第i级子平均, (0-1)-c表示在无限长的时段里的平均, (∞)-c表示在无限小的时段里的平均值, 那么可以得到c
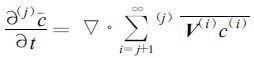
|
(7) |
均运动中的湍流通量为j +1直至∞级通量之和。与式 (1) 、(3) 相同, 只考虑垂直方向的扩散, 将式 (7) 右方的求和写成平均时段的积分的形式, 且用通常的平均符号表示j级平均符号, 则有
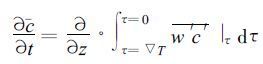
|
(8) |
根据Taylor冻结理论, 式 (8) 可写为
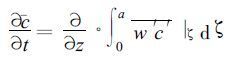
|
(9) |
式 (9) 中的ζ表示形成该通量的湍涡的空间尺度, a表示最大涡的尺度, 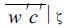

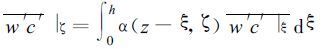
|
(10) |
在这里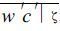
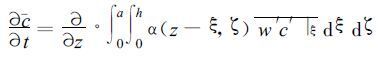
|
(11) |
若取
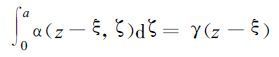
|
(12) |
γ(z-ξ) 具有长度的倒数的量纲。将式 (12) 代入式 (11) 可得:
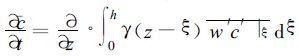
|
(13) |
式 (12) 表明湍流区域内的各层的非局地湍流通量是通过局地湍流而相互关联的, 且满足以下关系:
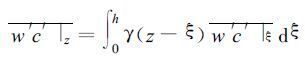
|
(14) |
显然, 在常通量层里
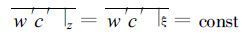
|
(15) |
因此
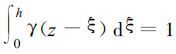
|
(16) |
在离散的情况下, 上式为:
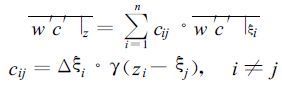
|
(17) |
这里cij就相当于是湍涡的非局地交换系数, 应该满足下式
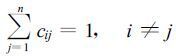
|
(18) |
因此, 欲按式 (15) 求得z高度上的湍流通量, 则需首先求得各层次的局地通量以及湍涡的非局地交换系数cij, 本文用青藏高原的近地层观测试验资料计算感热通量, 并与实测数据作了对比。
2 局地感热通量的多尺度湍流理论计算方法文献[17]从多尺度分解概念出发, 建立了多尺度Reynolds方程组, 并将子尺度运动处理为描述质点个别运动的Langevin形式, 推导出感热输送通量的表达式:
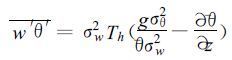
|
(19) |
其中θ为平均位温; σw为局地垂直风速标准差; σθ为局地位温变化标准差; Th为Lag range湍流时间尺度, 它的倒数为温度脉动时间尺度与垂直速度脉动时间尺度的倒数和 (称“并联和”), 脉动时间尺度可以通过大气湍流的多尺度分解所求得的相关函数的线性组合而得到[15]。因此, 根据式 (19) 能够具体计算出感热通量。
式 (19) 与式 (1) 形式相同, 式 (19) 中的σw2Th就相当于式 (1) 中的kc。事实上, 这里的γc仍然可以是由局地平均位温、重力加速度、局地位温和垂直速度的脉动均方差决定的。
因此在高纬度寒冷地区γc较大; 地形复杂地区σw较大, 如果σθ不是很大, γc就较小; 反之平坦地区气流平稳, 这时只要σθ不是很小, γc就较大。θ、σw与σθ都可以用观测取得, Lagrange湍流时间尺度Th的求取方法为:
(1) 按以下公式分别计算w′和θ′的自相关系数
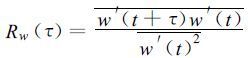
|
(20) |
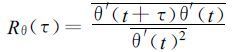
|
(21) |
(2) 对式 (20) 、(21) 进行指数分解[15]
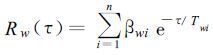
|
(22) |
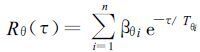
|
(23) |
其中, Twi为第i阶湍涡的自相关时间尺度, 它与自身的尺度成正比。βwi为第i阶湍涡动能对整个大湍涡动能的比值。计算中是根据观测资料直接算出垂直风速功率谱, 再通过快速傅立叶逆变换求得相关函数Rw(τ)。使用Wiscombe等[18]指数拟合法直接求得βwi和Twi的值, 以后再用下式求取局地总体Euler时间尺度。
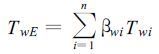
|
(24) |
根据关系式[16]
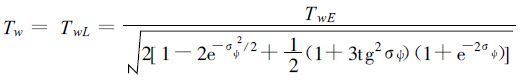
|
(25) |
将Eluer时间尺度转换成Langrange时间尺度TwL, 式中σψ为风向脉动标准差。
对于Tθ的计算方法同于TwL的计算, 只是未用式 (25) 将温度脉动的Eluer时间尺度转换为Langrange时间尺度, 因为上述关系是针对风速脉动导出的, 目前还不知道温度脉动的Eluer与Langrange时间尺度之间的关系。
(3) 按公式[17]
求取热通量的时间尺度Th。式中Tw和Tθ分别为垂直速度w′和θ′的Lag range自相关时间尺度。
3 非局地交换系数cij的确定非局地交换系数是湍流穿越理论中的核心问题之一, 尚未能从理论上完全解决。从实际应用的角度出发, Stull [11]提出了几个方法, 如平流相似 (Analogy with advection)、大涡相似 (Similarity theory for large eddies)、谱相似 (Spectral similarity) 和由Richardson数等构成的强迫函数 (Forcing Function) 法。这里借用强迫函数法的思路来求取非局地交换系数。Stull提出的计算法如下:
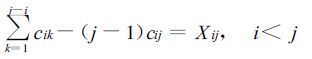
|
(27) |
这里i=1是最靠近地面的格点, Xij为强迫函数。式 (27) 中cij的系数 (j-1) 及加项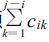
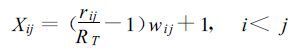
|
(28) |
rij是i和j点之间的总体Richardson数, RT是湍流终止的临界Richardson数。距离加权因子wij定义为
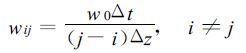
|
(29) |
这里Δt是时间步长, Δz是格距, w0是湍流的特征垂直速度尺度。在本文所讨论的问题中, 对该计算方案仅进行诊断性的应用。因此式 (29) 改为
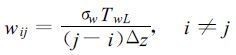
|
(30) |
按式 (27) 、(28) 和 (30) 解出cij以后, 再按式 (18) 的要求进行归一, 即取
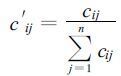
|
(31) |
再令
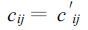
|
(32) |
本文在用青藏高原TIPEX试验资料计算感热通量时, 式 (27) 改为
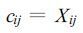
|
(33) |
式 (28) 中的wij取为1。
4 局地感热通量的相似理论计算方法在经典相似理论中, 地表层风速梯度、温度梯度和Monin-Obukhov长度L分别表示为[19]

|
(34) |
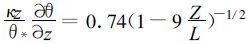
|
(35) |

|
(36) |
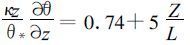
|
(37) |
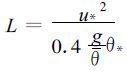
|
(38) |
其中κ为卡门常数, 取0.35。将式 (34) 和式 (35) 或式 (36) 和式 (37) 与式 (38) 联立, 用迭代法可求出L, 然后求出u*、θ*, 最后按照式 (39) 得到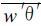
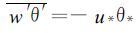
|
(39) |
1998年5月10日~8月10日, 我国开展了第二次青藏高原大气科学试验 (TIPEX), 其中大气边界层综合观测基地共设4个站, 即当雄、改则、昌都和那曲[20]。本文采用昌都站的边界层观测资料, 分别用感热通量的非局地多尺度湍流计算方法和经典相似理论计算感热通量, 并与实测值进行比较。
昌都地区位于青藏高原的东南部。TIPEX昌都观测站设在昌都郊外南北走向的河谷地段 (31°06′N, 97°16′E), 海拔高度3227 m, 距昌都城区约5 km, 观测场下垫面较为平坦, 东西宽500多米, 南北长4~5 km, 西邻澜沧江, 东西两侧为200~400 m高的南北走向的连绵山脉, 观测站地面为约50 cm深的沙渍黄土。5月下旬起, 雨季到来, 水汽充沛, 地表开始有稀疏的杂草生长, 6月末杂草长至约20 cm高。据分析[20], 昌都站的地表粗糙度为2.5 cm左右。观测站四周景观基本可代表青藏高原东南部地区高山峡谷的地形地貌和植被特征。TIPEX昌都观测站使用的湍流探测仪器为日本KAIJO公司生产的DA600-3T超声风温仪, 用涡动相关法测量三维风速和温度的脉动值, 观测高度4 m, 采样频率10 Hz。此外设立了一个气象观测桅塔, 用于小时平均的风速和温度值的梯度观测, 桅塔梯度观测测点高度为16、8、4、2、1、0.5 m。梯度观测系统由芬兰VAISALA公司的温度和湿度传感器、长春气象仪器厂的三杯式脉冲信号型风速传感器、美国YOUNG公司的风向传感器和澳大利亚DEC公司的DT-60采样器组成。
5.2 近地层观测资料的计算结果与分析对昌都的观测数据分别用相似理论和感热通量的非局地多尺度湍流计算方法进行计算, 为避免丢失有用信息, 所用的TIPEX释放的原始资料均未作挑选, 全部参与统计, 每组资料长度不少于60 min, 每秒探测到10组温度和风速瞬时值。
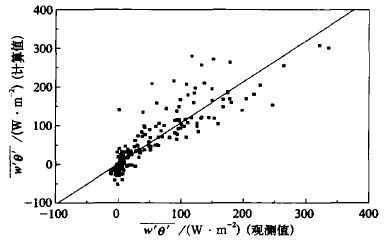
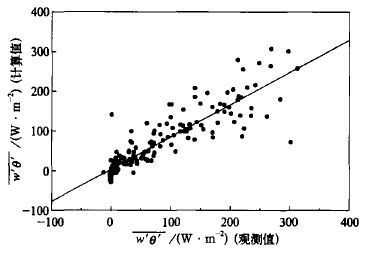
TIPEX昌都站点1998年5月18日00 :00至5月31日24 :00温度和风速脉动量的观测时间长度达到1 h的资料有274组。昌都地区的干湿季以5月23日为分界线[20], 24~29日期间出现了5次6 mm以下的降水。图1为用多尺度湍流理论计算出的感热通量与昌都观测数据的线性相关, 相关系数为0.90。在计算中, 274组数据都得到了有效使用。图2为经典相似理论计算出的感热通量与昌都实测值的线性相关, 相关系数为0.895。
|
|
| 图 1. 非局地多尺度湍流的计算值与昌都观测值的相关 (R=0.90, n=274, y=1.06 x +1.23) | |
|
|
| 图 2. 经典相似理论的计算值与昌都观测值的相关 (R=0.895, n=185, y=0.81 x +3.65) | |
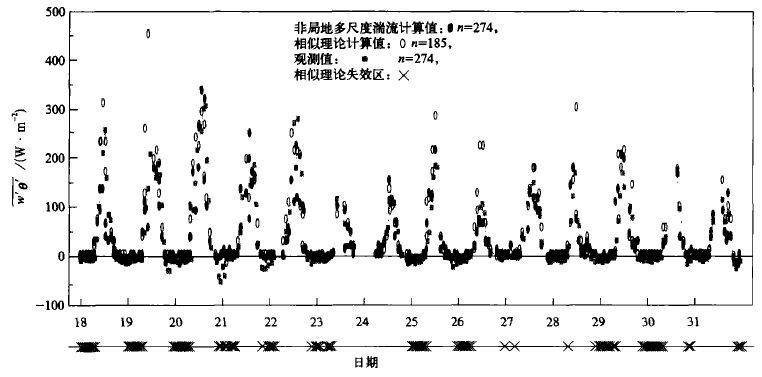
图3为多尺度湍流理论和相似理论计算值与观测值比较的时间序列变化, 可以看出两个理论的计算值与实测值都符合比较好。但是相似理论无法计算的资料达89组, 占28 %, 主要出现在大气稳定度为近中性的时段。这是因为在用迭代法求Monin-Obukhov长度L时, 计算不收敛, 运算陷入无限循环, 无法求出L值。这些数据在过去往往作为存在观测误差而被舍去。
|
|
| 图 3. 1998年5月昌都近地面层湍流热通量计算值与观测值的比较 | |
用经典相似理论在计算感热通量时不收敛的原因可能有两方面。第一, 相似理论认为, 近中性层结条件下的感热通量应该是接近于零的。但由于地表结构的不均匀性, 对太阳辐射的吸收就会有差异, 造成地表上层的温度水平涨落, 只要某一局部的地表温度比周围高, 就会有热量向上输送。而且这种次平均尺度上的热量输送不仅出现在地表层上, 在边界层的任一高度上, 只要存在水平方向上局部温度高于周围温度时, 就会产生向上的热量输送。因此, 即使在温度的平均垂直梯度近似为零的状态下, 还会观测到向上的热通量。此外, 昌都的海拔高度有3200多米, 空气密度大约为海平面的一半多一点, 其热容量相对也小。地表的水平热力不均匀性将会产生相对大的温度脉动, 从而有利于地面和不同高度上的次尺度温度涨落所造成的“对流”发展。这种所谓的“对流”和超绝热条件下的强烈发展的热泡对流是不同的, 前者是由温度的湍流脉动涨落驱动的; 后者是强大的地面整体加热的效应, 其对流有时呈现有结构的状态, 有时呈现湍流状态。此外, 在超绝热条件下, 当混合层充分发展时、大气位温上下混合均匀, 尽管垂直温度层结的表观呈现近中性状态, 但是仍旧会有较强的热通量向上输送, 其中包括“大涡”输送。这样的观测资料用经典相似理论计算感热通量时就会出现计算不收敛, 无法得到结果。
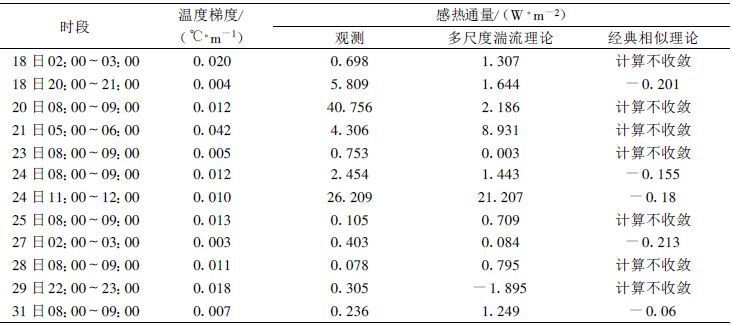
第二, 相似理论中温度梯度为正时, 感热通量一定是从上向下输送的。但是同样由于大气边界层中水平热力结构不均匀性产生的温度涨落, 也会导致在大气弱稳定的状态下出现逆梯度输送的现象, 这时用经典相似理论计算感热通量也会出现计算发散的现象, 或者是计算值与观测值的符号相反。在昌都观测资料中, 共出现12次稳定层结条件下的热量逆梯度输送现象, 用多尺度湍流理论能将其中11次的感热通量输送方向计算正确 (表1)。朱蓉等[21]用南极中山站近地层湍流试验资料验证多尺度湍流理论的感热通量公式的结果也表明, 多尺度湍流理论能计算出逆梯度输送的感热通量。
在昌都的观测试验中大气层结为近中性的状况下, 用经典相似理论计算感热通量时, 不但计算出现发散的情况多, 而且可计算出的结果与实测值的差距较大; 而用非局地多尺度湍流计算方法能计算所有的资料, 并且基本能将感热通量的输送方向计算正确, 但部分资料的计算结果在数值上还存在较大误差。由此可见, 多尺度湍流理论的感热通量表达式, 不仅经过严格的理论推导, 物理意义明确, 而且能够反映出真实大气近地层热量输送的特性。但多尺度湍流理论毕竟还是一个新生的理论, 有待于进一步发展完善。
|
|
表 1 1998年5月昌都站观测到热量逆梯度输送时多尺度湍流理论与经典相似理论的计算结果 |
6 结论
在大气边界层多尺度湍流理论和湍流穿越理论的基础上建立的大气边界层感热通量的非局地多尺度湍流计算方法, 用于计算青藏高原昌都TIPEX站的近地面层感热通量, 通过与大气湍流相似理论计算结果进行对比分析后, 可以得到以下几个结论:
(1) 在计算近地层大气的热量湍流输送时, 感热通量的非局地多尺度湍流计算方法比经典相似理论有更大的应用范围, 计算结果更合理, 能很好地描述稳定层结下的感热逆输送现象。
(2) 在大气边界层参数化的研究中应该加强对温度、垂直速度脉动及湍流拉氏尺度进行参数化的试验研究。
致谢 感谢中国气象科学研究院卞林根研究员为本文提供了青藏高原近地层观测资料。| [1] | Wyngaard J C, Brost R A, Top-down and bottom-up diffusion of a scalar in the convective boundary layer. J Atmos Sci, 1984, 41: 102–112. DOI:10.1175/1520-0469(1984)041<0102:TDABUD>2.0.CO;2 |
| [2] | Holtslag A A M, Moeng C-H, Eddy diffusivity and counter-gradient transport in the convective atmospheric boundary layer. J Atmos Sci, 1991, 48: 1690–1698. DOI:10.1175/1520-0469(1991)048<1690:EDACTI>2.0.CO;2 |
| [3] | Stull R B, Review of non-local mixing in turbulent atmospheres:Transilient turbulence theory. Bound-Layer Meteor, 1993, 62: 21–96. DOI:10.1007/BF00705546 |
| [4] | Deardorff J W, Theoretical expression for the counter-gradient vertical heat flux. J Geophys Res, 1972, 77: 5900–5904. DOI:10.1029/JC077i030p05900 |
| [5] | Troen I, Mahrt L, A simple model of the atmospheric boundary layer sensitivity to surface evaporation. Bound-Layer Meteor, 1972, 37: 129–148. |
| [6] | Stull R B, Static stability:An update. Bull Amer Meteor Soc, 1991, 72: 1521–1529. DOI:10.1175/1520-0477(1991)072<1521:SSU>2.0.CO;2 |
| [7] | Mellor G L, Yamada T, A hierarchy of turbulence closure model for planetary boundary layers. J Atmos Sci, 1974, 31: 1792–1806. |
| [8] | Benoit R, Cote J, Mailhot J, Inclusion of a TKE boundary layer parameterization in the Canadian regional finite-element model. Mon Wea Rev, 1989, 117: 1726–1750. DOI:10.1175/1520-0493(1989)117<1726:IOATBL>2.0.CO;2 |
| [9] | Pan Z, Benjamin S, Brown J M, et al. Comparative experiments with MAPS on different parameterization schemes for surface moisture flux and boundary layer processes. Mon Wea Rev, 1994, 122: 449–470. DOI:10.1175/1520-0493(1994)122<0449:CEWMOD>2.0.CO;2 |
| [10] | Hong S-Y, Pan H-L, Non-local boundary layer vertical diffusion in a medium-range forecast model. Mon Wea Rev, 1996, 124: 2322–2339. DOI:10.1175/1520-0493(1996)124<2322:NBLVDI>2.0.CO;2 |
| [11] | Stull R B, Transilient turbulcnce theory. Part I:The concept of eddy mixing across finite distances. J Atmos Sci, 1984, 41: 3351–3367. DOI:10.1175/1520-0469(1984)041<3351:TTTPIT>2.0.CO;2 |
| [12] | Stull R B, Transilient Turbulence Theory. Part Ⅱ:Turbulent Adjustment. J Atmos Sci, 1984, 41: 3368–3379. DOI:10.1175/1520-0469(1984)041<3368:TTTPIT>2.0.CO;2 |
| [13] | Holtslag A A M, Boville B A, Local versus nonlocal boundary layer diffusion in a global climatc model. J Climate, 1993, 6: 1825–1842. DOI:10.1175/1520-0442(1993)006<1825:LVNBLD>2.0.CO;2 |
| [14] | Holtslag A A M, Bruijn I F, Pan H-L, A high resolution air mass transformation model for short-range weather forecasting. Mon Wea Rev, 1990, 118: 1561–1575. DOI:10.1175/1520-0493(1990)118<1561:AHRAMT>2.0.CO;2 |
| [15] | 徐大海. 关于不同尺度大气运动中的雷诺交换. 气象学报, 1992, 50, (3): 257–271. |
| [16] | 徐大海. 多尺度大气湍流的扩散及扩散率. 气象学报, 1989, 47, (3): 302–311. |
| [17] | 徐大海. Lagrange与Euler时间积分尺度之间关系的统计动力学物理模型. 气象学报, 1992, 50, (2): 138–151. |
| [18] | Wiscombe W L, Evans L W, Exponential-sum fitting of radiative transmission. J comput Phys, 1977, 24: 416–444. DOI:10.1016/0021-9991(77)90031-6 |
| [19] | 赵德山, 徐大海, 李宗恺, 等. 城市大气污染总量控制方法手册. 北京: 中国环境科学出版社, 1991: 91-92;104. |
| [20] | 周明煜, 徐祥德, 卞林根, 等. 青藏高原大气边界层观测分析与动力研究. 北京: 气象出版社, 2000: 1-2,17~21. |
| [21] | 朱蓉, 徐大海, 卞林根, 等. 南极近地层大气的热量逆输送现象. 气象学报, 2000, 58, (2): 214–222. |
 2005, 16 (3): 273-282
2005, 16 (3): 273-282