引言

太阳辐射是地球上最基本、最重要的能源。它在地表上分配的变化，会根本地改变温度、湿度、降水和大气环流特征。因此，地表辐射研究在国内外一些重大的研究计划中一直备受重视^[1~3]。气候变化作为全球变化研究的一个重要组成部分，是当今国内外研究的热点问题之一。以往的研究工作，大都集中在探讨温度、降水等气象要素的气候变化规律上，而对于太阳辐射的气候变化研究相对较少。

目前，全世界仅有太阳辐射观测站一千多个，其中，我国约有一百多个。因此，仅仅依靠观测资料来描述太阳辐射的空间分布是相当困难的^[4~5]。本文利用黄河流域及其周边35个日射站资料建立了用日照百分率拟合太阳总辐射的估算式，之后结合获得的经验系数，采用黄河流域及其周边164个常规气象站日照百分率资料，对黄河流域1960~2000年逐月太阳总辐射进行了拟合计算，获得了黄河流域太阳总辐射的空间分布，并对其气候变化的时空分布规律进行了探讨。

1 资料来源及数据处理

所用资料包括黄河流域及其周边164个常规气象站建站至2001年日照百分率资料和35个日射站1957~2001年太阳总辐射资料，其中，日照百分率为月平均值，辐射资料为月总量值 (其单位为MJ·m^-2)。对所用资料进行了严格的质量检测和筛选，并对辐射资料进行单位转换，即:转换为月平均日总量资料，其单位为MJ·m^-2·d^-1。

2 黄河流域太阳总辐射的研究方法

大量研究表明^[6~8]:太阳总辐射Q与日照百分率s之间存在良好的相关关系，即:

(1)

其中，Q为太阳总辐射，Q₀为天文辐射，a、b为经验系数。

根据式 (1)，结合35个日射站总辐射的实测资料来获取黄河流域总辐射拟合的经验系数a、b。为了分析经验系数随时间、地点的变化特性，探讨不同时空尺度太阳总辐射拟合模型的有效性，根据不同的数据集群程度，分别建立了下列太阳总辐射估算式:

① 单站分月模型:将单个日射站、同月份太阳总辐射集群作为一个样本，分别建立各日射站各月太阳总辐射估算式 (样本数量:35 ×12=420);

② 单站全年模型:将各日射站全年所有月份太阳总辐射集群作为一个样本，分别建立各站年太阳总辐射估算式 (样本数量:35);

③ 分月模型:将35个日射站同月份太阳总辐射集群作为一个样本，建立各月太阳总辐射估算式 (样本数量:12);

④ 综合模型:将35个日射站所有月份太阳总辐射集群作为一个样本，建立综合统一的太阳总辐射估算式 (样本数量:1)

通过对比分析发现，在综合考虑总辐射拟合式 (1) 中经验系数空间变化和时间变化的情形下，使用“单站分月模型”建立的总辐射拟合精度最高。为此，运用单站分月模型来估算黄河流域太阳总辐射。

黄河流域太阳总辐射计算步骤如下:

① 利用地理信息系统ArcGIS 8.1，采用逆距离加权插值法 (IDW)，将单站分月模型获得的黄河流域及其周边35个日射站1~12月总辐射估算的经验系数a、b进行空间内插，生成黄河流域及其周边1~12月总辐射估算经验系数a、b的空间分布图;

② 由总辐射估算经验系数a、b的空间分布图，读取黄河流域及其周边164个常规气象站1~12月总辐射估算的经验系数;

③ 根据确定的经验系数，结合164个常规气象站的日照百分率观测资料，对每个站1960~2000年逐月太阳总辐射进行计算;

④ 用IDW插值法求出164个常规气象站总辐射计算结果在空间上的分布情况，并用黄河流域界线提取出黄河流域1960~2000年逐月太阳总辐射空间分布图;

⑤ 根据黄河流域逐月太阳总辐射空间分布图，借助地理信息系统ArcGIS 8.1获得流域平均的年和季节特征序列。其中，季节划分是以3~5月为春季、6~8月为夏季、9~11月为秋季、12月至翌年2月为冬季。

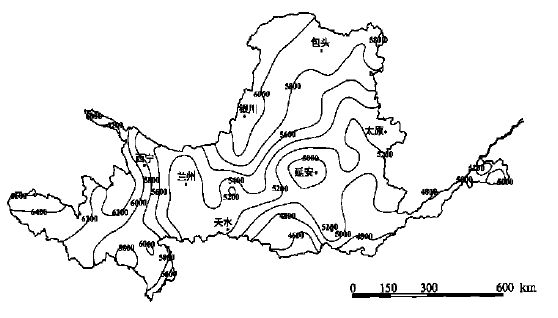
3 黄河流域总辐射的气候变化规律 3.1 年总辐射量的空间分布特征

由黄河流域多年平均年太阳总辐射量的空间分布图 (图 1) 可看出，黄河流域年太阳总辐射主要表现为由东南向西北增加的趋势，兰州站以西的青海高原区为最高，年总辐射量在5600~6500 MJ·m^-2·a^-1; 河套平原、鄂尔多斯高原为次高值区，年总辐射量在5600~6000 MJ·m^-2·a^-1; 东部华北平原区最小，年总辐射量在4500~5000 MJ·m^-2·a^-1。

3.2 气候变化趋势

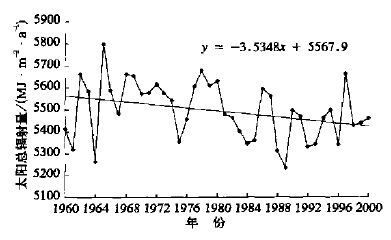
由图 2可看出黄河流域近年来太阳总辐射呈明显下降趋势，这与全球太阳总辐射下降的研究结论相一致。图中直线为总辐射变化的线性拟合趋势线，通过了99 %的信度检验。

对黄河流域不同年代总辐射量统计表明:20世纪60~70年代的年总辐射量相当，80~90年代相当。黄河流域年总辐射量在20世纪80~90年代较60~70年代下降了108.78 MJ·m^-2·a^-1，下降幅度约为1.96 %。在季节上，夏季总辐射具有同样的特点，20世纪80~90年代较60~70年代下降了62.53 MJ·m^-2，下降幅度为3.4 %; 不同年代比较而言，冬季总辐射呈持续下降趋势，20世纪90年代较60年代下降了33.34 MJ·m^-2，下降幅度为3.6 %。春季和秋季太阳总辐射量的年代变化不明显。

3.3 气候倾向率空间分布

将太阳总辐射的趋势变化用一次线性方程来拟合，即

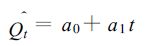
(2)

其中，t为自然时间序列 (年)，a₀、a₁为系数，a₁·10称为气候倾向率。根据式 (2) 计算1960~2000年每个台站的年和季节总辐射量的气候倾向率，之后由ArcGIS 8.1生成其空间分布图。

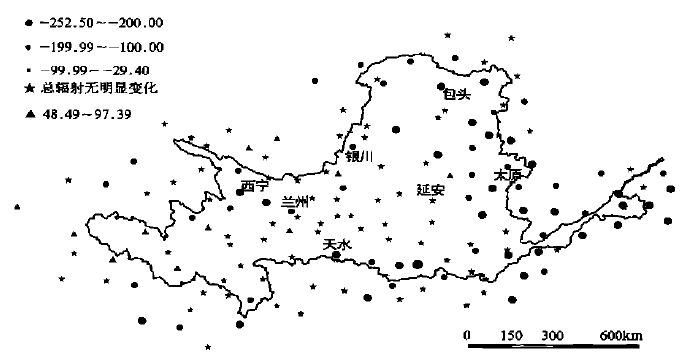
图 3给出了黄河流域太阳总辐射气候倾向率的空间分布，图中“ ”表示总辐射呈上升趋势; “”表示总辐射呈下降趋势，所有总辐射上升 (下降) 台站均通过了95 %的信度检验。虽然黄河流域整体平均太阳总辐射呈下降趋势，但局部区域与整个流域的气候变化趋势并不完全同步。由图 3可看出，黄河流域年总辐射量下降的区域主要集中在流域东部的山西及河南、山东等华北平原区，其次为上游青海湖东部的西宁、民和、门源等地以及河套地区和秦岭山脉周边地区等。有少部分地区年总辐射量呈上升趋势，主要出现在流域上游源区的玛多、达日、同德等地。从年总辐射量的气候倾向率的数值来看，年总辐射量下降的幅度要比上升大得多，每10年二者的极端值分别为-252.50 MJ·m^-2·a^-1和97.39MJ·m^-2·a^-1。

由黄河流域四季太阳总辐射气候倾向率空间分布图 (图 4) 可看出，春季和秋季整个黄河流域总辐射量除局部地区略有增减外，基本上没有变化; 夏季和冬季总辐射量发生变化的区域与年总辐射量变化形式基本一致，只是范围上略有变化。

4 结论

(1) 1960~2000年黄河流域年总辐射量呈明显下降趋势，不同年代比较而言，20世纪60~70年代的年总辐射量相当，80~90年代相当，80~90年代较60~70年代下降了108.78 MJ·m^-2·a^-1，下降幅度约为1.96 %。

(2) 黄河流域年总辐射量下降的区域主要集中在流域东部的山西及河南、山东等华北平原区，其次为上游青海湖东部的西宁、民和、门源等地以及河套地区和秦岭山脉周边地区等。

(3) 在季节上，太阳总辐射的下降主要表现在夏季和冬季。其中，夏季总辐射量在20世纪80~90年代较60~70年代下降了62.53 MJ·m^-2，下降幅度为3.4 %; 不同年代比较而言，冬季总辐射呈持续下降趋势，20世纪90年代较60年代下降了33.34 MJ·m^-2，下降幅度为3.6 %。春季和秋季太阳总辐射量基本上没有明显变化。