2. 北京大学大气科学系, 北京 100871
2. Department of Atmospheric Science, Peking University, Beijing 100871
准确估计地面某一段时间降水量的重要性,是不言而喻的。例如水库、河流的水资源调节; 抗洪抢险中的洪水预报,特别是对泥石流的爆发及山体塌方等预报方面将起着关键作用[1~3]。由于全国在几年内将建成新一代多普勒天气雷达观测网,使得用雷达估算降水在广大地区成为现实。雷达可以在5~6 min (由扫描模式决定) 时间内完成一次体扫,回波强度探测的空间分辨率为1 km, 是目前时空分辨率最好的降水测量工具。本文尝试用卡尔曼滤波法来校正雷达定量估算区域降水,并对影响估算结果的参数进行了分析。
卡尔曼滤波是由数学家卡尔曼于1960年针对随机过程状态估计首先提出的。之后,卡尔曼滤波在信号处理、最优控制、航天等领域得到广泛应用。20世纪90年代初,Daley就明确指出伴随变分和卡尔曼滤波是大气数据同化的未来发展方向。现已被广泛地用于数据同化[4~8],分析数值模拟中的初始场。国内有人将卡尔曼滤波用于某些气象要素的预报[9~11],但还没有见到用于雷达定量估测区域降水量的文献报导。卡尔曼滤波法定量估测降水起源于对校准因子G/R的分析,例如单点校准法[12]和平均校准法[13]。1976年Cain等人[14]在雨量计标定雷达估计区域降水量中,首次用统计方法分析G/R序列,认为其对数序列服从正态分布,并用模拟的方法进行了测试。Ahnert等人[15]于1983年在为美国下一代天气雷达 (NEXRAD) 设计降水处理系统 (PPS) 时认为,用雷达数据定量测量降水时,不管怎样努力去保持高水准的数据精度,仍然会存在误差。其产生误差的原因有很多,在雷达估测降水过程中有时会产生均匀的倍乘偏差,假定这个偏差服从“随机行走过程”,就可用离散的卡尔曼滤波来消除,Hudlow等人[16]也有类似的论述。Ahnert等人[17~18]用数值模拟的方法首次验证了卡尔曼滤波法测量降水的有效性和稳定性,认为与简单计算G/ R相比,卡尔曼滤波法有以下优势:当更新平均偏差场时卡尔曼滤波考虑了测量噪声; 在计算偏差时可提供估算误差; 可避免G/R的不稳定性; 可对未来1h作降水预报。O′Bannon等人[19]用Oklahoma冬季的实际降水资料对美国NEXRAD降水子系统进行测试,了解卡尔曼滤波某些参数值设置对降水测量精度的影响。以后,Smith等人[20]和Dah-Syang等人[21]在上述工作的基础上对卡尔曼滤波测量降水进行了改进和完善。现在卡尔曼滤波法估测降水已成为美国NEXRAD雷达降水处理子系统的一部分,其特点是既能保证一定的精度又能满足实时处理的要求。
1 卡尔曼滤波校准法原理影响雷达降水测量精度的主要原因有[22]:雷达标定及其参数不稳定; 地物及异常传播的影响; 电磁波受到阻碍物遮挡; 衰减; 对雨滴谱的假设; 反射率因子垂直廓线的变化; 雷达波束的不完全充塞等。卡尔曼滤波校准方法主要对由于Z-R关系的不稳定、雷达硬件的标定偏差、湿天线罩的衰减及雨区衰减等造成的测雨误差进行订正。设偏差校准因子f=Ig(t)/ Ir(t) 为一随机变量,Ig为某一时刻雨量计测得的降水强度,Ir为同一时刻雷达测得的降水强度。卡尔曼滤波的基本思想是:若随机变量f的两个独立估计值f1、f2可以由不同的方程而获得,则f的最佳估计值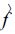
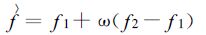
|
(1) |
确定权重ω的准则是要以使得校准后的最佳估计值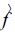
根据张培昌等[12]所述的原理,将偏差转换为对数形式,可得到如下一组卡尔曼滤波迭代公式
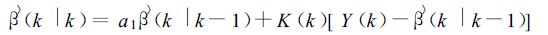
|
(2) |
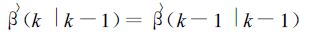
|
(3) |
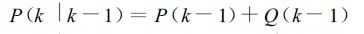
|
(4) |
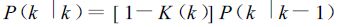
|
(5) |
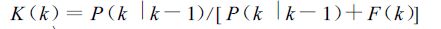
|
(6) |
在式 (2)~(6) 中,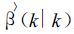
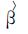
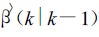
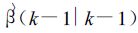
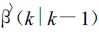
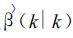
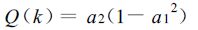
|
(7) |
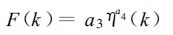
|
(8) |
a1,a2,a3,a4为参数。η(k) 表示第k小时有降水的雨量计总数,若已知迭代初始值,就可求出最优的f估计值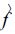
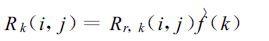
|
(9) |
Rr, k表示雷达探测的降水强度。
在假定对数偏差服从正态分布的情况下,根据式 (2)~(6) 估算出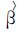

采用卡尔曼滤波校准方法,可直接求得各时间间隔内网格点的降水强度,进行时空累加,就可获得区域降水总量,其基本原理如下:
设雷达测量区域为S,累加的时段为T,则把S分成n个网格小块,并把T时段分成k个时间间隔,即
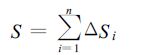
|
(10) |
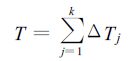
|
(11) |
那么,第i个小块在T时段的降水量Mi为:
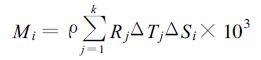
|
(12) |
式 (12) 中ρ为水的密度 (单位:t/m3),Rj为第j个时间间隔内的降水强度 (单位:mm/h),ΔSi为网格面积 (单位:km2),则S区域上的降水总量M(单位:t) 为:
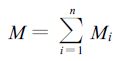
|
(13) |
用卡尔曼滤波法估测降水,需要输入估计降水时刻前若干时次未订正雷达降水资料和雨量计资料,资料越多,估算精度越好。读入这些数据后,就可用卡尔曼滤波迭代公式计算降水。
利用卡尔曼滤波法估算降水在输入各时次雷达和与其相应的雨量计数据后,必须求得每一时次的参数a1、a2、a3、a4,一般用极大似然法求解,由极大似然函数求偏导并令其为0,得到一组非线性方程组,此方程组不能得到解析解,只能用数值解法求其近似解。本文为简单起见,参考文献[20]给定其值。在求解过程中,Q(k) 和F (k)的值分别由式 (7) 和式 (8) 计算。其算法如下:①输入N时次雷达、雨量计数据; ②给定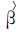
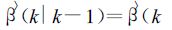
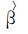
使用2002年7月22日16:00(北京时,下同) 至24:00宜昌CIN RAD/SA雷达数据和湖北、湖南两省的雨量计资料进行数值试验,资料来源于2002年中国气象局“973”项目的野外观测试验。其当日的天气形势为08:00 500 hPa图上副热带高压势力较强,长江中下游地区受槽前西南气流影响,700 hPa和850 hPa暖式切变线北抬,位于江苏南部、安徽南部到湖北南部,切变线东段有所减弱,西段南侧的西南急流仍较强。湖北省境内2002年7月22~24日为持续阴雨天气,并出现了大范围的降雨。
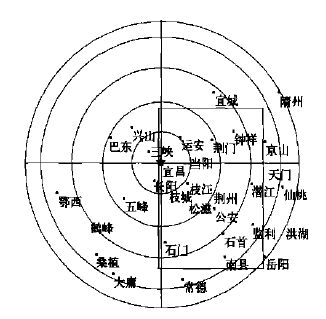
根据雨量计分布和雷达站周围的地形情况,采用雷达的1.5°PPI资料,其估算的区域见图 1中所包含的方框内。
|
|
| 图 1. 雨量计相对于雷达站 (★宜昌) 位置图 | |
4.2 参数的设置
由雨量计估算的结果是使用Cressman方法进行内插得到的 (其参数C=0.6);Z-R关系的参数a=300,b=1.4;假定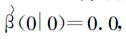
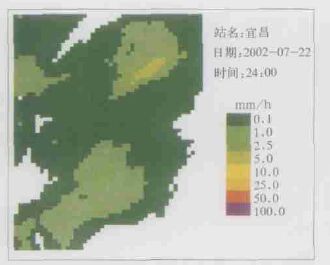
未订正前雷达估测的区域降水量见彩图 2。由彩图 2可知,在估算区域的东北部及南部有较强的降水区域。未订正前雷达估测的区域降水量为3.2343 ×107t, 与雨量计估算的降水量8.4774 ×107t相比,其相对误差为61.85 %。
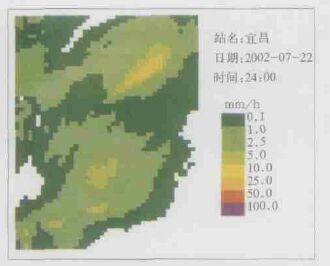
卡尔曼滤波方法估算的区域降水量 (彩图 3) 基本上反映了雷达估算降水的结构:在估算区域东北方向及南偏西方向估算前有较强降水,订正后仍是较强的区域; 同时融合了雨量计测值局地准确的特点:在估算区域东北方向及南偏西方向订正后降水有所增强。由卡尔曼滤波方法估算的区域降水量为6.9370 ×107t, 与雨量计估算的降水量8.4774 ×107t相比其相对误差为18.17 %,可见其计算精度有了很大的提高。
|
|
| 图 2. 未订正前雷达估算的域降水场 | |
|
|
| 图 3. 卡尔曼滤波法估算的区域降水场 | |
4.4 卡尔曼滤波法参数对计算结果的影响
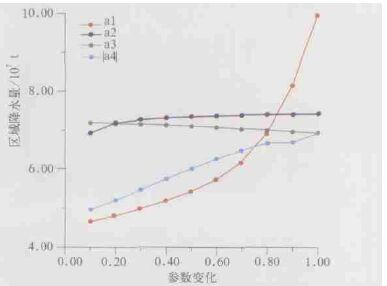
彩图 4反映了参数a1、a2、a3、|a4|的变化对计算结果的影响,计算结果对a1、|a4|较敏感,a2、a3对计算结果影响不大。当a1值逐渐变大时,估算的区域降水量亦逐渐增大,当a1=0.1时,估算的区域降水总量为4.88 ×107t; 当a1=1.0时,估算的区域降水总量为11.07 ×107t。事实上,a1取较小值时,表示偏差过程在降水云体内随着时间的变化波动很大。由式 (7) 可知,此时状态方程的误差方差变得较大,因而估算的结果与“标准值”比较误差亦较大 (“标准值”即由原来参数计算的结果); 当a1=1.0时,表示偏差过程只随不同的降水云体变化,而在整个降水云体的生消过程中保持不变,由式 (7) 可知,此时状态方程的误差方差为0。当a2、a3由0.1增大到1.0,估算的区域降水量变化都不大,而且两者相差也不大,并且都有较好的计算结果,但它们形成的机理是不相同。曲线a2,并不是因为样品偏差 (即雷达估算降水量的偏差值) 特别的精确,根据式 (7) 可知,而是与状态方程误差方差有关。曲线a3,由于匹配的雨量计数大都不小于10个,根据式 (8) 可知,若a3取最大值1.0,此时观测方程的误差方差已经小于0.1,形成曲线a3的原因是,观测方程的误差方差较小,因而当a3变小时对提高估算结果的精度影响不大。这也说明了a2、a3从0.1增大到1.0时,其计算结果的变化趋势的不同。由彩图 4可以看出,当a4从-0.1变化到-1.0时,卡尔曼滤波的估算结果变得越来越接近于“标准”计测值。根据式 (8) 可知,a4处于误差方差的指数位置,因而当a4从-0.1减小到-1.0时,误差方差逐渐减小。
|
|
| 图 4. 卡尔曼滤波法估算区域降水景随参数的变化 | |
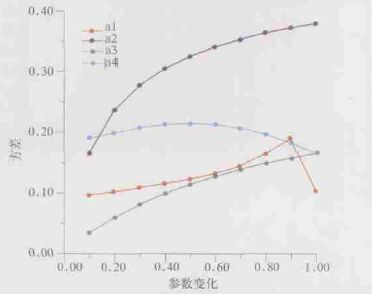
卡尔曼滤波后输出值与状态值之间的误差方差P (k)(即偏差方差) 随参数a1、a2、a3及|a4|的变化见彩图 5。由彩图 5可知,偏差方差随着a1从0.1增大到0.9而逐渐增大; 但当a1=1.0时,又突然减小到0.1042。由式 (7) 及 (4) 不难发现其原因:当a1为1.0时,Q=0。当a2由0.1增大到1.0时,P (k) 明显增大,从式 (7) 可知,Q随着a2呈线性变化。偏差方差P (k)随参数a3增大而增大,随参数|a4|开始时是缓慢增大,后又缓慢减小。
|
|
| 图 5. 卡尔曼滤波法诂算方差随参数的变化 | |
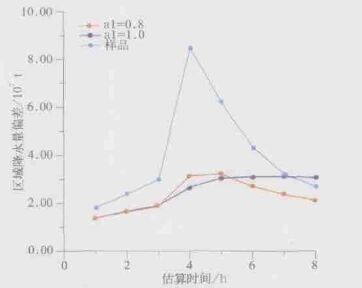
彩图 6表示是a1分别取0.8及1.0时估算区域降水量偏差及样品偏差 (未经滤波的雷达实际估测区域降水量偏差) 所得估算结果随观测时间的变化。由彩图 6可见,当a1=1.0时,估算的区域降水量偏差没有反映样品偏差的变化,而是随着时间的变化逐渐增大; 而当a1=0.8时,其变化基本上与样品偏差变化趋势一致,只是波动的幅度要小得多。
|
|
| 图 6. 区域降水量估算偏差及样品偏差随时间的变化 | |
彩图 7表示a1分别取0.8及1.0时区域降水量估算偏差方差随估算时间的变化。由彩图 7可见,当a1=0.8时,其随时间变化曲线的波动比a1=1.0时要大,而且其数值也比后者时要大。图中开始时偏差方差较小是由于初值的原因 (取得较小)

|
|
| 图 7. 区域降水暈估算方差随时间的变化 | |
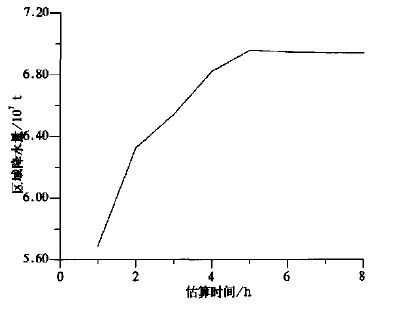
观测时次的增加 (每小时估算降水为1时次),即2002年7月22日23:00~24:00,估算1次; 2002年7月22日22:00~24:00,估算2次等等,依次类推。观测时次变化对卡尔曼滤波估计精度的影响见图 8。由图 8可知,开始时,随着观测时次的增加,其区域降水估算精度迅速提高,当观测次数达到5次后,其估算值变化较缓慢。
|
|
| 图 8. 区域降水量估算值随观测次数变化 | |
5 小结与讨论
本文根据卡尔曼滤波校准方法的原理,利用2002年“973”项目野外观测资料进行了试验,并分析了各参数对估算结果的影响,得出如下结论:
(1) 卡尔曼滤波校准法能有效提高雷达定量测量区域降水量的精度,并能较好地体现雷达测量降水场结构精细的特点。
(2) 影响卡尔曼滤波估算精度较大的因子是a1和a4,对估算偏差方差值影响较大的参数是a2。
(3) 随着观测次数的增加,卡尔曼滤波估计的精度越来越高。
本研究的不足之处是在卡尔曼滤波校准法试验过程中如何对参数进行实时计算没有考虑,同时还应用更多的个例进行验证。
| [1] | Thomas T W, Edward A B, Sun Juanzhen, et al. Prediction of a flash flood in complex terrain. Part Ⅰ: A comparison of rainfall estimates from radar, and very short range rainfall simulations from a dynamic model and an automated algorithmic system. J Appl Meteor, 2000, 39, (6): 797–814. DOI:10.1175/1520-0450(2000)039<0797:POAFFI>2.0.CO;2 |
| [2] | David N Y, Thohas T W, Leavesley G H, Prediction of a flash flood in complex terrain. Part Ⅱ: A comparsion of flood discharge simulation using rainfall input from radar, a dynamic model, and an automated algorithmic system. J Appl Meteor, 2000, 39, (6): 815–825. DOI:10.1175/1520-0450(2000)039<0815:POAFFI>2.0.CO;2 |
| [3] | Limaye A S, Stellman K, Improving Flood Prediction Using Kalman Filter, Mesoscale Atmospheric Model Forecasts and Radar-based Rainfall Estimates. 16th Conf on Hydrology, Orlando, Florida: AMS, 2002: 127–129. |
| [4] | 高山红, 吴增茂, 谢红琴. Kalman滤波在气象数据同化中的发展与应用. 地球科学进展, 2000, 15, (5): 571–575. |
| [5] | Hansen J A, Accounting for model error in ensemble-based state estimation and forecasting. Mon Wea Rev, 2002, 130: 2373–2391. DOI:10.1175/1520-0493(2002)130<2373:AFMEIE>2.0.CO;2 |
| [6] | Burgers G, Van Leeuwen P J, Evensen G, Analysis scheme in the ensemble Kalman filter. Mon Wea Rev, 1998, 126: 1719–1924. DOI:10.1175/1520-0493(1998)126<1719:ASITEK>2.0.CO;2 |
| [7] | Houtekamer P L, Mitchell H L, Data assimilation using an ensemble Kalman filter technique. Mon Wea Rev, 1998, 126: 796–811. DOI:10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2 |
| [8] | Evensen G, Van Leeuwen P J, Assimilation of Geosat data for the Agulhas current using the ensemble Kalman filter with a quasigeostrophic model. Mon Wea Rev, 1996, 124: 85–96. DOI:10.1175/1520-0493(1996)124<0085:AOGADF>2.0.CO;2 |
| [9] | 陆如华, 徐传玉, 张玲, 等. 卡尔曼滤波的初值计算方法及其应用. 应用气象学报, 1997, 8, (1): 34–43. |
| [10] | 周筱兰, 张礼平. 卡尔曼滤波方法在制作长期月平均气温预报中的应用.暴雨·灾害. 北京: 气象出版社, 1999. |
| [11] | 卢峰本. 卡尔曼滤波在沿海冬半年风力预报中的应用. 气象, 2002, 24, (2): 50–53. |
| [12] | 张培昌, 杜秉玉, 戴铁丕. 雷达气象学. 北京: 气象出版社, 2001. |
| [13] | Wilso J W, Brandes E A, Radar measurement of Rainfall-A summary. BAMS, 1979, 60, (9): 1048–1058. DOI:10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 |
| [14] | Cain D E, Smith P L, Operational Adjustment of Radar Estimated Rainfall with Gage Data: A Statistical Evaluation. Preprints of 17th Radar Meteor Conf, Boston: AMS, 1976: 533–538. |
| [15] | Ahnert P, Hudlow M, Johnson E, et al. Proposed "on-site" Precipitation Processing System for NEXRAD. Preprints of 21st Radar Meteor Conf, Boston: AMS, 1983: 378–385. |
| [16] | Hudlow M D, Greene D R, Ahnert P R, et al. Proposed Off-site Precipitation Processing System for NEXRAD. Preprints of 21st Radar Meteor Conf, Boston: AMS, 1983: 394–403. |
| [17] | Ahnert P R, Hudlow M D, Johnson E R, Validation of the "on-site" Precipitation Process system for NEXRAD. Preprints of 22nd Radar Meteor Conf, Boston: AMS, 1984: 192–201. |
| [18] | Ahnert P R, Krajewski W F, Johnson E R, Kalman Filter Estimation of Radar-rainfall Field Bias. Preprints of 23rd Radar Meteor Conf, Snowmass: AMS, 1986: JP33–JP37. |
| [19] | O′Bannon T, Ahnert P, A Study of the Precipitation Processing System on a Winter-type Oklahoma Rainstorm. Preprints of 23rd Radar Meteorology Conf, Boston: AMS, 1986: JP99–JP102. |
| [20] | Smith J A, Krajewski W F, Estimation of the mean field bias of radar-rainfall estimates. J Appl Meteor, 1991, 30: 397–412. DOI:10.1175/1520-0450(1991)030<0397:EOTMFB>2.0.CO;2 |
| [21] | Dah-Syang Lin, Krajewski W F, Recursive Methods of Estimating Radar-rainfall Field Bias. Preprints of 24th Radar Meteor Conf, Boston: AMS, 1987: 648–651. |
| [22] | Harrison D L, Driscoll S J D, Kitchen M, Improving precipitation estimates from weather radar using quality control and correction techniques. Meteor Appl, 2000, 7, (2): 135–144. DOI:10.1017/S1350482700001468 |
| [23] | Rodriguez-Iturbe I, Mejia J, The design of rainfall networks in time and space. Water Resources Research, 1974, 10: 731–728. |
 2005, 16 (2): 213-219
2005, 16 (2): 213-219

