水圈的运动不仅反映了天气气候的变化规律,而且也较强地影响着天气气候的变化。对水圈的研究分为两支:一支是对地表径流变化规律的研究,另一支则是对大气水汽收支及其运动规律的研究。联系这两者的关键因子便是降水再循环率,其定义为:一个地区的蒸发对该地区降水的贡献。它表征着一个地区陆面水文与区域气候相互作用的强弱。只有在对一个地区降水再循环率做出评估后,才能清楚在该地区的降水中有多少来自本地区的蒸发,有多少来自该地区以外的水汽流。因此对一个地区降水再循环率做出评估,也是对该地区水量收支描述所必须的一步。
早在20世纪20年代,就已经开始对一些江河流域的再循环降水进行评估,但那时资料不全,而且所用的评估模式都是很简单的一维模式,因此当时的评估结果与最近的重新评估结果相差较大。Brubaker等人[1]建立了一个二维的降水再循环模式,并利用NOAAGFDL (Geophysical Fluid Dynamics Laboratory) 的数据,对以下地区降水再循环率进行了评估和比较:北美的Mississippi流域、南美的Amazon流域、前苏联地区的欧洲部分以及非洲的Niger流域。Eltahir等人[2~3]从水汽守恒方程出发,重建了对降水再循环率的评估模式,利用欧洲中心ECMWF (European Center for Medium-range Weather Forecasts) 再分析资料和GFDL的数据,对Amazon流域重新进行了评估。该文还指出以往对水汽循环评估过高的原因在于其理论假设有问题。伊兰[4]在Eltahir模式的基础上,引进水汽通量的线性平均,重建了类似Eltahir的评估模式,并利用ECMWF资料对长江流域的降水再循环率进行了评估。Trenberth等人[5]利用NCEP/NCA R再分析资料对全球的降水再循环率分布做出了评估。孙岚等人[6]利用GCM模式结果对全球的降水再循环率分布做出了预测。Szeto[7]对加拿大Machanzie流域进行了评估,并分析了地形特征与大尺度天气活动对降水再循环率分布的影响。Wood等人[8]也利用GCM模式结果对Amazon、Mechazie和Mississippi流域的降水再循环率分布做出了预测。
本文选取32.5°~42.5°N,95°~120°E作为研究区域,其长度尺度 (面积的平方根) 是1600 km, 它涵盖了我国北方的全部地区。整个黄河流域位于其中心地带。对这一研究区域降水再循环率的评估,能清楚地展示陆面蒸发对黄河全流域降水的贡献。本文将利用1976~1995年共20年的NCEP/NCAR再分析数据,评估所研究区域的降水再循环率,揭示其空间分布形势,研究其季节变化特征; 利用NCEP/NCAR资料中8层水汽含量数据,计算大气的水汽输送,展示黄河流域水汽来源及其随季节变化特征; 通过对比两个10年蒸发率、降水率和降水再循环率的状况,揭示气候变化的影响程度。
1 降水再循环率评估模式本文将采用Eltahir等人[2~3]提出的降水再循环率评估模式。根据降水再循环率定义,有
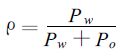
|
(1) |
式 (1) 中,ρ是降水再循环率; Pw是在某一格区上,来自研究区域内的水汽所形成的降水; Po是在某一格区上,来自研究区域外的水汽所形成的降水 (格区和研究区域是两个概念。考虑到NCEP/NCAR再分析资料的压力层数据空间分辨率是2.5°×2.5°,研究区域则包含了11 ×7个格区)
边界层实验数据显示,水汽分子从地表蒸发起来后,在15 min内能混合到1 km的高度。据此可以假定水汽分子在边界层内是充分混合的。这是该模式的第一个假设。由此,降水再循环率又可以定义为
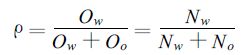
|
(2) |
式 (2) 中,Ow是从某一格区流出的来自研究区域内的水汽分子数; Oo是从某一格区流出的来自研究区域外的水汽分子数; Nw是在某一格区内空气中包含的来自研究区域内的水汽分子数; No是在某一格区内空气中包含的来自研究区域内的水汽分子数。
实验数据[2]显示,空气中水汽含量的变化率要比水汽通量小三个量级,比蒸发小两个量级。因此可以假定空气中水汽含量的变化率是小量,这样一来水汽守恒方程可以简化为:
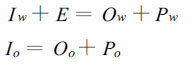
|
(3) |
其中,Iw是流入某一格区的来自研究区域内的水汽分子数,Io是流入某一格区的来自研究区域外的水汽分子数,E是该格区上蒸发的水汽分子数。
最终,可以得出如下形式的降水再循环率评估公式:
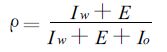
|
(4) |
该模式与以前的模式相比有两方面的优点:一是它可以揭示降水再循环率的空间分布; 另一方面,对资料空间分辨率以上的尺度,它不需要假定地表蒸发和降水均匀。本文采用式 (4) 作为评估公式。
2 资料与评估方法评估过程采用逐次逼近技术。具体步骤如下:
(1) 利用NCEP/NCAR压力层数据和表面层数据,分别计算出研究区域内各网格点上的水汽通量和蒸发率,并解码直接得到降水率。考虑到压力层数据的空间分辨率是2.5°×2.5°,而表面层数据的空间分辨率是1.875°×1.875°,为取得统一,将表面层上的蒸发率和降水率插值到压力层网格点上。
(2) 在各网格内给定ρ的初估值。根据式 (2) 分配各网格点上的Ow和Oo, 它们实际上也是进入临近格点的Iw和Io, 由公式 (4) 重新评估各格点内的ρ。如此迭代,直到前后两次差值小于给定的阈值。迭代收敛很快,一般是20步之内可以收敛6个量级。
(3) 为了求得某月k整个研究区域的总降水再循环率ρt(k),不能简单地将各网格区内的ρ求和平均,必须考虑降水归一化处理后作为权函数,如下式
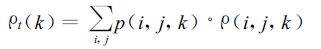
|
(5) |
p (i, j, k)是格区(i, j)内的k月降水率与该月该地区总降水量的比值。
(4) 同样为求格区 (i, j) 全年的总降水再循环率,也必须用降水归一化处理后作为权函数,如下式
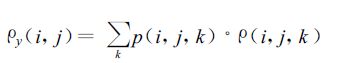
|
(6) |
p (i, j, k)是格区 (i, j) 内的k月降水率与该格区全年总降水量的比值。
从以上评估过程来看,需要NCEP/NCAR两方面的数据:
(1) 为计算水汽通量,需要各压力层上的速度、温度、相对湿度。NCEP/NCAR可以提供17层的温度和经纬向速度,以及8层相对湿度数据。压力层数据的空间分辨率是2.5°×2.5°,全球共144 ×73 ×17个格点。水汽通量计算公式
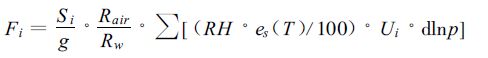
|
(7) |
i=1,2分别表示经向和纬向,RH是相对湿度,T是温度,es是饱和水汽压,p是压力,Rair和Rw分别是空气和水汽的气体常数,g是重力常数,L是垂直于水汽流方向的尺度。
(2) 地表蒸发和降水数据。NCEP/NCAR可以提供地表潜热通量和降水数据,其空间分辨率是1.875°×1.875°,全球共192 ×94个格点。地表蒸发可由潜热通量求出,
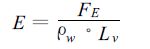
|
(8) |
式 (8) 中,FE是潜热通量,Lv是蒸发潜热,ρw是水汽密度。由于Eltahir的降水再循环率评估模式对地表蒸发数据在时间的连续性上和空间的规范化上要求高,目前国际上对降水再循环率评估通常用再分析资料[2,4,6,8]。
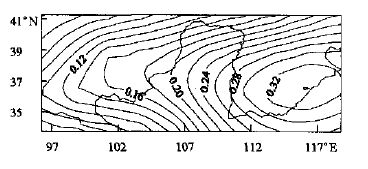
3 结果分析 3.1 降水再循环率的空间分布和季节变化图 1是我国北方地区1976~1995年总的年降水再循环率的空间分布。在37°N以北,降水再循环率等值线由西北向东南增加,这表明在37°N以北的地区,主要是西北风将当地蒸发的水汽带到黄河中下游; 在37°N以南,降水再循环率等值线由西南向东北增加,这表明在37°N以南的地区,来自青藏高原西北部的充足的水汽,进入黄河上游后,主要在西风的作用下,带到了黄河中下游 (图略)。尤其在黄河下游,有三分之一的降水是由研究区域的蒸发贡献的。黄河上游的降水再循环率低于15 %,可见这里的降雨超过85 %来自研究地区以外的水汽。由公式 (5)、(6) 利用降水作为权函数,计算出黄河流域总的降水再循环率只有19 %,这表明只有19 %的降水来自当地的水汽蒸发,其他81 %降水来自外部的水汽流入。Eltahir等人[3]结果显示Amazon流域 (长度尺度是2500 km) 总的降水再循环率是25 %~35 %(Eltahir用两种不同的数据,因而得到两个结果),Brubaker等人[1]结果显示Mississippi流域 (长度尺度是1400 km) 总的降水再循环率是24 %。可见我国北方地区陆面水文与区域气候相互作用不是很强,但是这一地区陆面蒸散对黄河下游降水的总体贡献还是不容忽视的。
|
|
| 图 1. 我国北方地区1976~1995年总的年降水再循环率的空间分布 | |
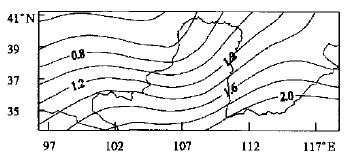
图 2是20年平均的蒸发率空间分布,它显示了较强的随纬度增加而递减的规律,该图也可以清晰地看到,由于北方来自蒙古地区冷空气的入侵,以及渤海湾暖湿空气对京津地区的影响,从而对蒸发等值线产生明显的波型。图 2也显示我国北方地区蒸发率不强,月平均蒸发量不到60 mm。这也是北方地区降水再循环率不高的重要原因。
|
|
| 图 2. 20年平均蒸发率空间分布 (单位:mm/ d) | |
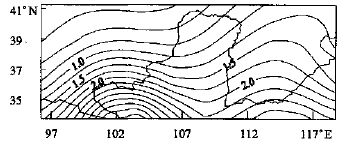
图 3是20年平均降水率空间分布,有两个降水集中的地区,一个位于黄河上游; 一个位于黄河下游以南,实际上它是长江下游降水中心向北的延伸。降水的空间分布与蒸发的空间分布对应得很好:降水大的地区,蒸发就相应增强。这可能是该地区植被覆盖不够,土壤含水量小,从而导致该地区的大部分降水直接被蒸发掉。这也说明该地区的蒸发不仅受温度变化的制约,而且也较强地受降水量的影响。下面还将结合蒸发和降水的季节变化和年际变化,更进一步讨论。
|
|
| 图 3. 20年平均降水率空间分布 (单位:mm/ d) | |
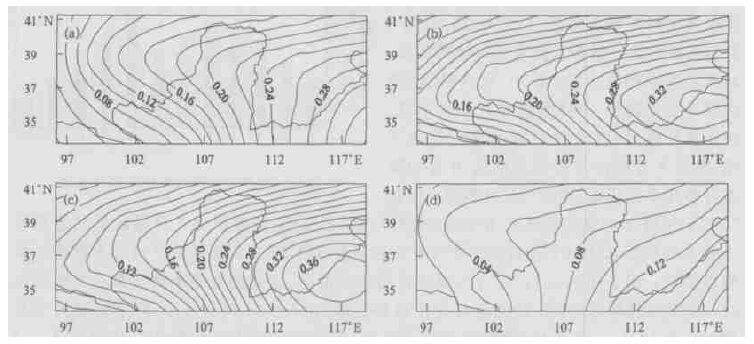
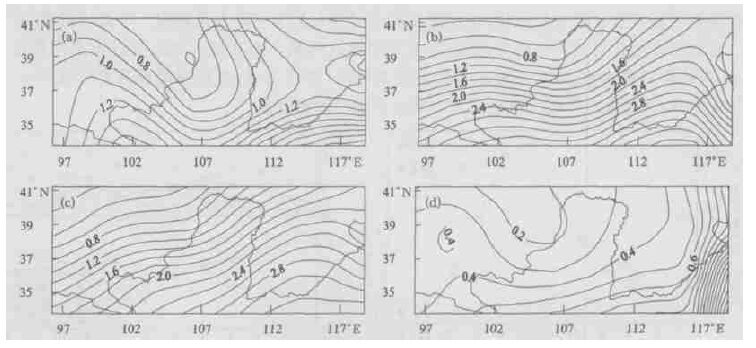
图 4是20年平均降水再循环率四季的空间分布。总的来说,秋季降水再循环率最高,冬季最低。四季的降水再循环率等值线基本上从西向东增加,这是因为黄河流域盛行的西风将上游的水汽带到下游所致。图 4b、c显示夏、秋两季降水再循环率分布相似,这是因为黄河上游在夏、秋两季均有明显的水汽辐合 (图略),使得这里降雨较大 (图略),图 5显示夏、秋两季蒸发均较强。由此出发的水汽流将更多从本地蒸发的水汽带往下游,从而形成夏、秋两季在研究区域的中东部的椭圆型的降水再循环率高值区。图 4b、c也展示了黄河上游的水汽蒸发对其中下游的影响路径和程度。图 4a、d显示春、冬两季降水再循环率分布相似。这是因为上游降水少 (图略),再者春、冬两季温度低,蒸发小 (图 5a、d),因而降水再循环率都很低。春、冬两季我国北方地区盛行西风,水汽也是从西部输往东部从使得降水再循环率由西向东增加。比较图 4和图 1,发现图 4b、c和图 1的分布相同,这表明总的降水再循环率主要由夏、秋两季决定,这是因为夏、秋两季降水强,所占的权重大。
|
|
| 图 4. 20年平均降水再循环率四季的空间分布 (a) 春,(b) 夏,(c) 秋,(d) 冬 | |
图 5是20年平均蒸发率四季的空间分布。总的来说,四季的蒸发率表现出均随纬度的增加而减少的规律。但在春、冬两季蒸发率的空间分布图 (图 5a,d) 上,可以发现研究区域的中北部出现一个很强的舌状低值区,这是来自北方冷空气的入侵而导致的蒸发率减少。在冬季,图 5d显示大陆地区蒸发不仅弱,而且变化很小,但在东南角海洋上蒸发急剧增加,这是大陆和海洋的蒸发在冬季有显著差异所致。
|
|
| 图 5. 20年平均蒸发率四季的空间分布 (单位:mm·d-1) (a) 春,(b) 夏,(c) 秋,(d) 冬 | |
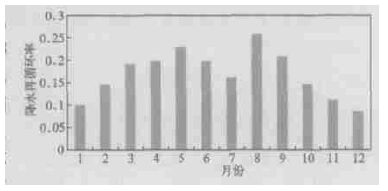
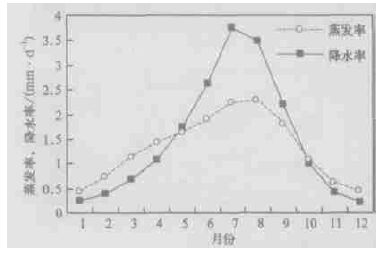
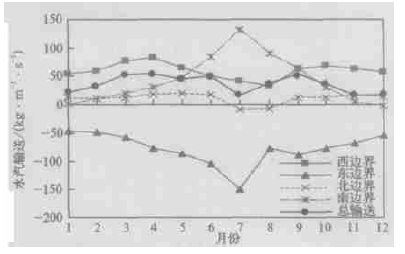
图 6是降水再循环率逐月变化趋势。降水再循环率在8月最强,达0.26,可见8月份有四分之一的降水是来自本地的蒸发。对照蒸发率和降水率 (图 7)、水汽输送 (图 8) 逐月变化趋势,可以发现8月降水丰富,因而蒸发强,同时8月外部的水汽输送不强,因而8月的降水再循环率高,9月的降水再循环率也较高,原因与8月相同。但在图 6 20年平均降水再循环率月变化7月,虽然降水和蒸发都很强,但降水再循环率明显偏低,这是因为7月通过南北边界进出的水汽非常强 (图 8),使得降水中含有外部的水汽量增加,从而导致7月降水再循环率明显偏低。图 6还显示11、12、1月降水再循环率最弱,这是因为冬季蒸发率非常低的缘故。蒸发率和降水率 (图 7) 的逐月变化趋势显示,在6、7、8和9月中,降水明显大于蒸发,在11、12、1~4月份中,蒸发都要高于降水,这样就难于保住土壤墒情,尤其在2、3、4月,土壤水分亏损最大。由于我国北方地区土壤墒情低,植被覆盖率低,蒸发所需的水汽较强地依赖于降水的直接提供,因而蒸发的空间分布形态与降水很相似。下面还将看到,二者的年际变化对应得也很好,即基本上是同增或同减。图 8显示北边界进出水汽量很小,东边界只有水汽输出,该地区水汽主要来自西、南两边界,而且在降雨高峰的夏季6、7、8月中,来自南边界的水汽量均大于来自西边界的水汽量。
|
|
| 图 6. 20年平均降水再循环率月变化 | |
|
|
| 图 7. 20年平均蒸发率和降水率的月变化 | |
|
|
| 图 8. 20年平均各边界水汽输送和总水汽输送的月变化 | |
3.2 年际变化特征和两个10年对比分析
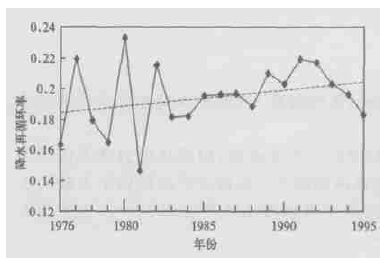
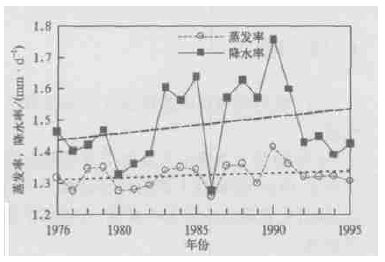
图 9是降水再循环率年际变化趋势。通过其变化趋势线可以发现降水再循环率在20年内逐渐增长,增幅是10 %。图 10是蒸发率和降水率的年际变化趋势,两者也都有一定的增长。蒸发率的增长与气候变暖有直接关系。图 10还显示蒸发率和降水率的年际变化趋势对应得很好,即:降水增加时,蒸发也相应增加。说明在我国北方地区,降水增加后,土壤墒情增加,蒸发也就随着增加。可见在我国北方地区,如何减少蒸发,保住墒情还是很紧迫的。
|
|
| 图 9. 区域平均降水再循环率的年际变化趋势 | |
|
|
| 图 10. 区域平均蒸发率和降水率的年际变化趋势 | |
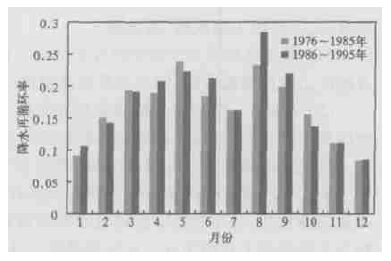
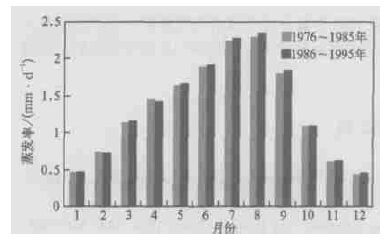
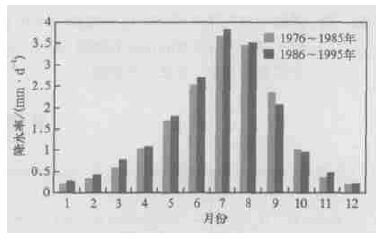
图 11是降水再循环率两个10年 (1976~1985年和1986~1995年) 比照情况。第二个10年的降水再循环率在6、8、9月有明显的增长,但在其他季节均有一定的下降。这说明在6、8、9月降水在第二个10年依赖本地蒸发的比率增高,其他月份依赖外部的水汽增加。图 12是蒸发率两个10年 (1976~1985和1986~1995) 比照情况。第二个10年的平均蒸发率在一年中5~9月有相对明显的增长,而在其他月份里,两个10年的蒸发率变化很小。这是因为在5~9月,我国北方地区降水大于蒸发 (图 7),土壤积蓄了一定的墒情,当温度增加时,能够蒸发更多的水汽,可见在5~9月,蒸发主要受温度制约。但在其他月份里,一方面,蒸发大于降水,土壤墒情低,即便是温度有些增加,蒸发所需的水汽也不够,因而蒸发主要受制于降水量; 另一方面,我国北方冬、春季温度很低,温度有少量的增长,还达不到蒸发所需的条件,所以两个10年在这些月份的蒸发变化不大。图 13是降水率两个10年 (1976~1985和1986~1995) 比照情况。第二个10年的降水率则在一年中大部分月份中均有增长。考虑到这仅是20年的数据资料,两个10年又紧邻,但气候变化对蒸发率、降水率和降水再循环率的影响已显现出来。
|
|
| 图 11. 降水再循环率两个10年对比 | |
|
|
| 图 12. 蒸发率两个10年对比 | |
|
|
| 图 13. 降水率两个10年对比 | |
4 结论
(1) 黄河流域总的降雨只有19 %来自当地的水汽蒸发,其他81 %降水来自外部的水汽流。
(2) 黄河上游降水主要由来自青藏高原较强的水汽所提供,因此这里的降水再循环率小于15 %,但黄河上游的降水蒸发后,在西风的输送下,为黄河下游提供了大量的水汽,通过汇合南北方向来的水汽,在黄河下游形成了降水再循环率达到30 %以上的椭圆形区域。
(3) 降水再循环率随季节变化差异较大,8月份的降水再循环率最高,达26 %,这是因为8月份降水充分,蒸发较强,而且水汽输送不显著; 而在11、12、1月的降水再循环率最弱,主要因为温度低,蒸发弱。
(4) 蒸发率和降水率的空间分布以及它们的年际变化都对应得很好。这表明我国北方地区土壤保墒能力低,降水很容易蒸发掉。
(5) 蒸发率、降水率和降水再循环率在20年中均有增加,表明气候变暖对我国北方地区的蒸发、降水和降水再循环的影响已经显现。
以上结论是根据NCEP/NCAR再分析资料得到的,Trenberth等人[5]曾对NCEP/NCAR资料水汽数据的精度在全球的分布有过评估,在中国北方地区水汽数据的精度还是比较满意的。但是,他们没对蒸发数据进行评估。因此,基于NCEP/NCAR再分析资料评估得到的上述结论有一定的局限性。目前的工作也只是对我国北方地区降水再循环率的初步评估,更进一步的评估则需要有时空上更完善的降水、蒸发、空气湿度和风场的实测资料。
致谢 感谢中国气象科学研究院孙岚博士与作者进行的有益讨论和提供相关资料。作者在加拿大MSC期间,Paul Whitfield在建模、Alex Cannon在获取和解码NCEP/ NCAR再分析资料方面提供了很多帮助,在此一并致谢!| [1] | Brubaker K L, Entekabi D, Eagleson P S, Estimation of continental precipitaton recycling. J Clim, 1993, 6: 1077–1089. DOI:10.1175/1520-0442(1993)006<1077:EOCPR>2.0.CO;2 |
| [2] | Eltahir E A B, Bars R L, Precipitation recycling in the Amonzon basin,. Q J R Meteorol Soc, 1994, 120: 861–880. DOI:10.1002/(ISSN)1477-870X |
| [3] | Eltahir E A B, Bars R L, Precipitation recycling. Rev Geophys, 1996, 34: 367–378. DOI:10.1029/96RG01927 |
| [4] | 伊兰. 亚洲季风的水循环与水分收支———GEWEX亚洲季风区实验 (GAM E) 预研究: [博士学位论文]. 北京: 中国科学院大气物理研究所, 1996. |
| [5] | Trenberth K E, Guillemot C J, Evaluation of the atmospheric moisture and hydrological cycle in the NCEP reanalyses. Climate Dyn, 1998, 14: 213–231. DOI:10.1007/s003820050219 |
| [6] | 孙岚, 吴国雄, 孙菽芬. 陆面过程对气候影响的数值模拟———SSiB与IAP/ LASG L9R15 AGCM耦合及其模式性能. 气象学报, 2000, 58, (2): 179–193. |
| [7] | Szeto K K, Moisture recycling over the Mackenzie Basin. Atmospere-ocean Special, 2002, 40: 181–197. DOI:10.3137/ao.400207 |
| [8] | Wood E F, Sheffield J. Analysis of GCM predicted precipitation recycling over large basins. 83rd Annual AMS meeting, Session 13, Climate Change Modeling: II. 14th Symposium on Global Change and Climate Variations, 2003. |
 2005, 16 (2): 139-147
2005, 16 (2): 139-147

