矩阵是数值代数中的一个基本概念,许多科学计算问题往往归结为对矩阵的操作。如在数值预报系统中,就要经常用到矩阵乘计算。因此,如何在超级计算机上高效地完成矩阵乘的计算,对提高许多数值预报模式的运行效率至关重要。
众所周知,在分布式主存并行计算机系统上,数据划分对数据并行程序运行效率影响重大。在进行大型矩阵计算时,由于受到机器内存容量的限制,必需进行数据传输,这些数据的移动要花费相当的通讯时间。因此,在分布式环境上设计矩阵运算的并行算法,不但要挖掘和开发其内在并行性,同时也要选择最优的数据分布形式,以减少数据通讯开销。
如果没有任何优化策略,两个N ×N阶矩阵相乘,标量运算复杂性为O〔N3〕。20世纪60年代末,Strassen[1]提出了一个新的快速算法,其标量运算只需O〔Nlog27〕。在分布式内存系统上,利用张量代数实现的公式化矩阵乘,使矩阵乘的计算效率大大提高了一步。在Nagesh Anupindi等人①②提出的算法中,矩阵采用列-行划分方式,从而省去了计算中乘数与被乘数的数据移动,只在求累加和时进行一次中间结果的置换。由于在许多大型科学计算中,数据更多地采用网格划分的方式,文献[2]中介绍了一种网格并行的Cannon算法,但其程序实现比较复杂。因此,我们在本文中提出一种新的矩阵乘网格划分算法。在IBM-SP计算机系统上的运行结果表明,新的网格划分算法容易实现,其通讯开销比列-行算法有所降低,其并行效率也有一定的提高,是一种有效的矩阵乘并行计算算法。
① Nagesh Anupindi, Qing Yang, Myoung An.Formulating Data-Partition and Migration in Distributed Memory Multiprocessors.(private communication)
② Nagesh Anupindi, Myoung An, Qing Ying.Parallel Matrix Multiplication Algorithm For Rectangular Arrays.(private communication)
1 矩阵乘列-行划分算法我们先讨论矩阵乘的列-行划分算法②。
设有N1 ×N2阶矩阵A及N2 ×N3阶矩阵B,计算N1 ×N3阶矩阵C :
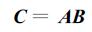
|
(1) |
设在分布式主存多机系统中共有k台处理机,这里总假定k能整除N1,N2,N3。将A按列、B按行均分于k台处理机上,结果,处理机i包含了A的第i个子列阵AN1×N2/k(i)、B的第i个子行阵BN2/ k ×N3(i)(0≤i≤k-1)。计算之前,我们将A(i)均分成k块:A(j,i),0≤j≤k-1。若结果C亦按行分布于各处理机上,即第t个处理机上C子行阵为CN1/k ×N3(t),则有
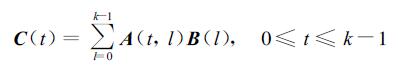
|
(2) |
在处理机i上,分别计算A(j,i)B(i),0≤j≤k-1,则k步计算之后,处理机i上为k个N1/k ×N3的子积矩阵块:
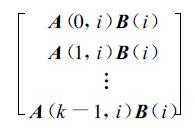
|
由于

|
(3) |
其中⊗为张量乘,I为恒等矩阵,P为跨步置换矩阵,其定义如下:
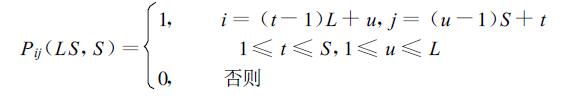
|
显然可见,处理机i经过k-1次与其它处理机的数据交换,即可得到C(i) 所有和数子积矩阵块。这相当于进行了一次矩阵置换,此刻的矩阵元素就是子积矩阵块。
最后,各处理机做子积矩阵累加,从而完成C各子行阵的计算:

|
(4) |
从算法的描述中可见,其主要计算为k次子矩阵乘法,子矩阵规模分别为A :(N1/k,N2/ k) 和B :(N2/k,N3)。数据通讯主要存在于最后的矩阵置换中,每个处理机均要与其它k-1个处理机进行数据交换,这可以用MPI的一个全互换函数 (MPI-A LLTOALL) 完成,其通讯开销为:
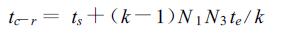
|
(5) |
这里,ts为通讯起步时间,te为单数据通讯时间。
在矩阵乘的列-行算法中,A,B两矩阵的划分方式是不一致的。下面我们来讨论一种网格划分算法,它比较易于与其它计算接口,且在一定程度上可减少通讯开销。
2 网格划分算法下面我们给出矩阵乘的网格划分算法。
同样针对式 (1),假定k=ks2,N1,N2,N3能被ks整除。现将A做网格划分并分配到各处理机上,记 (i,j) 处理机上的子矩阵块为A(i,j),将B按A同样的方式做网格划分,但在 (i,j) 处理机上分配B的 (j,i) 子矩阵块,即B(j,i),则有
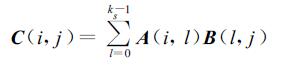
|
(6) |
如ks=3时,
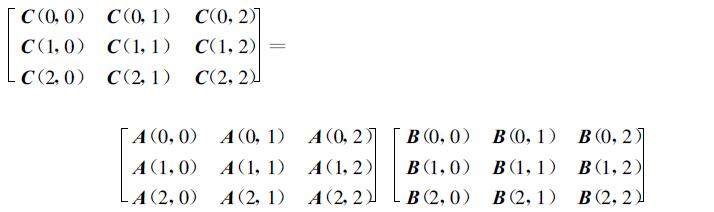
|
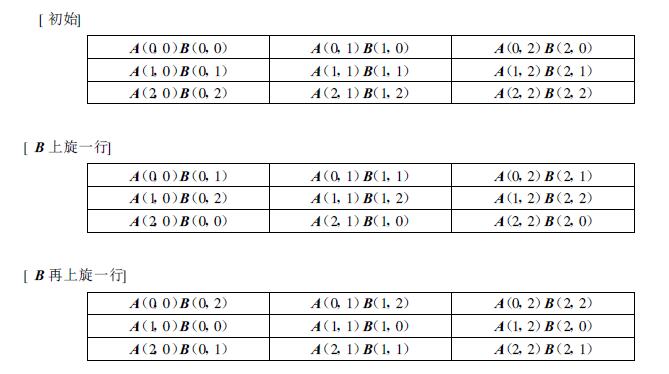
由于A(i,l) 与B(l,j) 同处于第l列处理机,因此总可以通过B在列上的移动而使它们处于同一处理机 (见图 1)。
|
|
| 图 1. 3×3处理机上的网格矩阵乘 | |
这样,对于一固定的C(i,j),其各加数A(i,l)B(l,j) 分处于第i行的各处理机上。而在某一处理机 (i,j) 上,ks-1步之后其所有子积矩阵块为:
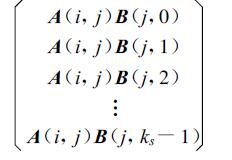
|
显然,在i行处理机上,有
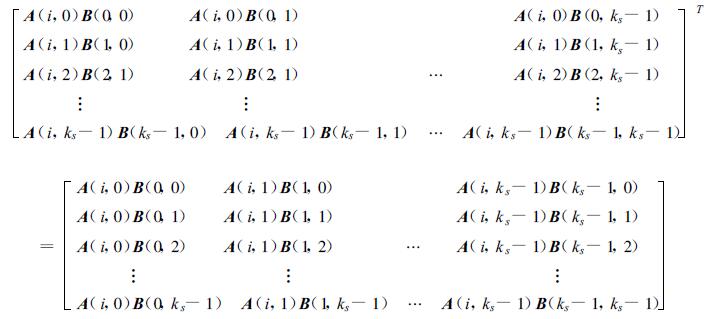
|
(7) |
于是,通过行处理机间以子积为元素矩阵的置换 (8),并在各处理机上做累加,即可得到C在各处理机上的子矩阵C(i,j),从而最终得到C。

|
(8) |
式 (8) 中,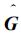
下面讨论一下此算法的计算开销和通讯开销。
从上面描述可以看到,计算主要为ks次子矩阵乘法,子矩阵规模为A :(N1/ks,N2/ ks) 和B :(N2/ ks,N3/ ks),通讯主要存在于计算子积时矩阵B的上旋及子积矩阵的置换。B的上旋共需进行 (ks-1) 次,每一次通讯块长度为N2N3/ k,通讯开销为:
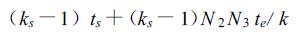
|
在做行间矩阵置换时,每个处理机须与同行ks-1个处理机各做一次数据交换,这同样可用一个MPI的全互换实现,其通讯开销为
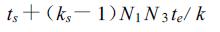
|
所以总的通讯开销

|
(9) |
将tmesh与式 (4) 的tc-r相减,有

|
(10) |
当N1=N2=N3=N,即A、B为方阵时,

|
(11) |
这时若

|
(12) |
则
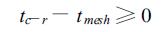
|
式 (12) 说明,对于方阵而言,当计算机条件一定时 (这时ts/ te为常数),网格并行计算在矩阵规模N较大时比列-行并行计算有效。将式 (12) 改写为如下形式:

|
(13) |
式 (13) 说明,在计算机条件一定且单处理机上矩阵元数个数一定时,矩阵规模越大,则网格并行计算的优势越大。
事实上,当矩阵不为方阵时,上述结论仍然成立,这里不再做一般性的推导。应该说明的是,上面所有的讨论都是以矩阵阶数可被处理机数整除为前提的,当矩阵不能被处理机数整除时,只要矩阵在数据分配时保证最优负载平衡,结论仍然可成立。
3 数值结果数值实验是在IBM-SP计算机上用Fort ran90 +MPI实现的[3],考虑到实际应用中矩阵计算多为方阵,因此程序设计上仅针对方阵进行了测试。实验用IBM-SP计算机共含有10个计算节点,每个节点含8个CPU,节点内为共享内存,节点间为分布式内存。计算机上提供并行计算环境poe和并行软件工具MPI。
表 1给出了矩阵乘运算在IBM-SP计算机上的几个测试结果。这里应该说明的是,测试结果与所用矩阵乘的串行算法关系密切。经过大量试算,我们选取了IBM公司工程与科学计算库提供的矩阵乘库函数作为基本的矩阵乘串行计算程序。
|
|
表 1 不同大小矩阵的测试 |
分析表 1,可以发现:矩阵乘的网格划分算法比列-行划分算法时间上有所改善,与列-行算法相比,网格划分算法平均改善了6 %左右。
表 2是为了将矩阵列-行算法和网格算法与串行计算比较而做的测试。由于串行计算规模受到机器内存的限制,我们选取矩阵大小为9216 ×9216。从表中可见,矩阵网格并行的加速比较矩阵列-行并行改善约10 %。
|
|
表 2 9216 ×9216在不同个数CPU运行时的时间比较 |
4 结论
矩阵计算是数值预报系统经常遇到的一个计算问题[4, 5],数值预报系统计算中许多问题的求解最终归结为对矩阵的计算。随着计算技术的不断发展[6],开展矩阵计算的研究对数值预报计算程序的高效实现是有意义的。
通过上面的讨论,我们认为:对于矩阵乘并行计算而言,在计算机条件一定时,随着矩阵规模的增大,采用网格并行计算不但能更好地与实际应用中的网格划分接口,而且能够进一步减少通讯开销,因而更具优势,是一种有效的矩阵乘计算方法。
由于目前所具有计算机条件的限制,没有能够对矩阵乘计算的一般性情况进行数值试验。今后一旦条件许可,我们将对矩阵计算做进一步深入的研究。
致谢 感谢国防科技大学李晓梅教授、宋君强教授和中国气象科学研究院金之雁研究员对论文作者的指导,他们与作者的讨论使作者受益匪浅。| [1] | Strassen V, Gaussian Elimination is Not Optinal. Numerical Mathematics, 1969, 13: 354–356. DOI:10.1007/BF02165411 |
| [2] | BarryWilkinson, MichaelAllen著. 陆鑫达译.并行程序设计. 北京: 机械工业出版社, 2002. |
| [3] | 都志辉著. 高性能计算并行编程技术———MPI并行程序设计. 北京: 清华大学出版社, 2001. |
| [4] | 李晓梅, 蒋增荣著. 并行算法. 长沙: 湖南科学技术出版社, 1992. |
| [5] | 施妙根, 顾丽珍编著. 科学和工程计算基础. 北京: 清华大学出版社, 1999. |
| [6] | 金之雁, 王鼎兴. 大规模数据并行问题的可扩展性分析. 应用气象学报, 2003, 14, (3): 369–374. |
 2005, 16 (1): 121-128
2005, 16 (1): 121-128



