数值预报的不确定性主要来源于大气初始状态的不确定性和预报模式的不确定性,大气运动的非线性特性决定了无论来自于初始场还是模式的极微小的误差在模式积分过程中将被放大,直至演变为较大的误差,Lorenz[1]首先指出这一现象。集合预报技术是目前减小这些误差的有效方法[2~5]。
在集合预报中,无论集合成员如何形成 (如通过在初始资料的基础上构造能表征其误差特征的扰动场形成集合成员[6],或通过选择不同的模式参数化方案、变化某些物理参数的值构成集合成员[7],或将不同数值模式作为集合成员[8],等等),每个成员的结果都代表了未来天气演变的一种可能性。综合所有成员的预报结果可以获得未来某种天气现象发生的相对概率 (如某地区发生大雨的概率),这在单一的模式预报中是无法做到的,与以往仅凭经验或用统计方法做出的概率预报相比,具有客观性和定量性,因而更具有参考价值。
如何根据各成员结果得到概率预报,最简单的方法是视每个成员的权重均等,根据预报发生某天气现象的成员个数来确定未来该天气现象发生的概率,如成员数为10个时,有5个成员预报未来24 h雨量达到大雨,则未来24 h发生大雨的概率为50 %,这是目前最常用的方法[6~8],本文暂称之为平均法。Hamill和Colucci[9, 10]提出了一种新的方法,首先应用一定次数的集合预报结果统计得到所有成员的等级分布 (Rank Distribution),根据这一分布和各成员的预报结果确定未来某天气现象发生的概率。试验结果表明该方法的预报效果好于平均法,这里暂称之为Rank法。
本文以MM5模式作为试验模式,通过选择物理过程的不同参数化方案产生8个集合成员,分别用平均法和Rank法对2001年11月至2002年5月期间的22个降水个例进行短期集合降水概率预报试验。此外本文提出另一种方法———相关法,即根据每个成员与预报对象的相关大小决定各成员在集合预报中的权重,根据所有成员的预报结果和权重得到概率预报。用该方法对上述22个个例进行试验,并对三种方法的试验结果进行比较。这些有助于将来开展短期集合降水概率预报业务。
1 试验模式与集合成员构成试验模式为PSU/NCAR的中尺度模式系统第五代第三版 (MM5V3)。
模式垂直方向取σ坐标,分不等距21层,顶层气压为100 hPa;水平格距取45 km,格点数为113 ×115,中心点位于31.17°N、121.43°E,整个计算区域的范围大致为:10°~50°N,100°~140°E。垂直速度定义在整σ层上,其余变量定义在半σ层上,水平网格采用“Arakaw a-Lamb B”跳点格式。
模式采用非静力方案,显式水汽方案为简单冰相方案,辐射方案为云辐射方案,地面温度取5层土壤模式,侧边界条件为松弛流入流出方案,模式没有考虑浅积云的作用。
与降水密切相关的积云参数化方案和边界层参数化方案采用不同方案,构成集合预报的8个成员 (表 1)。
|
|
表 1 集合成员的构成 |
2 试验个例
本文对2001年11月至2002年5月期间的22个降水个例进行短期集合降水概率预报试验。表 2给出了这22个个例的起始时间。2001年11月至2002年5月虽然不是汛期,但2002年春季雨水明显偏多,2002年4月和5月的12个个例的24 h最大雨量都达到了暴雨量级。
|
|
表 2 试验个例的起始时间 |
客观分析使用的初估场为NCEP的AVN全球1°×1°谱模式的分析场 (08 :00,北京时,下同) 和12 h预报场 (20 :00),实时观测资料包括地面常规资料、探空资料及测风资料。模式积分时间为48 h,时间步长为60 s。
3 概率预报方法本文分别用平均法、相关法和Rank法进行短期集合降水概率预报试验。
(1) 平均法
每个成员在集合预报中的权重均等为
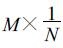
(2) 相关法
该方法在集合预报的基础上结合了统计的方法。根据积累的一定次数的集合预报结果和对应的实际降水情况统计各成员的预报与实况降水间的相关性,假设ri为第i个成员的预报与实况的相关系数,该成员在集合预报中的权重则为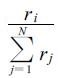
该方法也是集合与统计相结合的方法。
将N个集合成员按预报结果从小到大的次序排列形成N +1个等级 (Rank),与其对应的实况可能位于N +1个等级中的任一等级。当实况与所有成员的预报结果都不相同时确定其位于的等级比较简单,如8个集合成员的预报降水量 (从小到大) 分别为8、10、11、16、19、20、22和25 mm,若实况降水量为21 mm,则此时的实况位于9个等级中的第7等级。当实况与集合成员的预报结果相同时则需要进行技术处理才能确定其位于的等级,所谓技术处理就是在所有成员的预报结果及实况值上加上或减去小量级的随机量,这一处理不会影响概率预报结果。
积累一定次数的集合预报结果,判断每次预报对应的实况位于的等级,应用这些结果统计实况位于每个等级的概率即等级分布,有了这一分布再根据各成员的预报结果即可得到降水概率预报。
假设X1,X2,…,XN为N个成员的预报降水量 (从小到大),R1,R2,…,RN+1为N +1个等级分布,则未来发生V1≤V<V2的降水概率P为:
当V1=Xi-1, V2=Xi时, P=Ri
当V1=0, V2=Xi时, 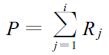
当V1=0, 0<V2<X1时, 
当V1=Xi, Xi<V2≤Xi +1时, 
当Xi<V1≤Xi+1, V2=Xi+1时, 
一般,降水量越大,其发生的概率越小,因此将发生大于XN的降水概率分布视为均等分布是不合理的。Rank法假设其分布服从Gumbel分布,F为Gumbel累积分布函数,则:
当V1=XN时, 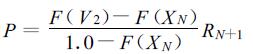
当V1>XN时, 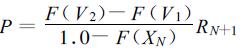
相关法和Rank法都需要积累一定次数的集合预报结果作为统计样本,为保证有一定量的样本,本文试验采用一种“交叉有效”技术,即对一个个例试验时,将其余21个个例的集合预报结果作为统计样本,而且对模式区域内2039个站点一视同仁,即不分开统计,这样每次试验时的统计样本可达到2039 ×21=42819个。
4 评价方法以模式区域内2039个站点的24 h降水概率预报结果作为统计对象,对三种方法的试验结果进行以下几方面的评价。
(1) RPS评分
RPS评分是对多个等级的概率预报结果进行综合评价的一个指标。若某预报对象有J个态,那么站点或格点的RPS评分值 (RRPS) 为:

|
其中Pi为站点或格点上某个态发生的预报概率,如果该态发生则Oi=1,没有发生则Oi=0。RRPS值在0~J-1的范围内,且越小越好,RRPS=0时概率预报最佳。
将降水按大小分为6类:24 h降水量V (单位:mm,下同)<0.1、0.1≤V<10、10≤V<25、25≤V<50、50≤V<100和V≥100,即J=6,统计2039个站点的平均RPS评分。
(2) BS评分
BS评分值RBS是对某个等级 (即某事件发生) 的概率预报结果进行评价的一个指标。

|
其中,Pi为第i个站点或格点上某事件发生的预报概率。如果该事件发生,则Oi=1;没有发生,则Oi=0。n为参加统计的站点或格点总数。显然RBS值在0~1的范围内,越小越好,RBS=0时,概率预报最佳。
将降水分成小雨 (0.1)、中雨 (10)、大雨 (25)、暴雨 (50) 和大暴雨 (100) 等5个量级,分别评价24 h发生各量级以上降水的概率预报结果。
(3) ROC曲线
ROC(即相对作用特征) 曲线也是被用以对某个等级的概率预报结果进行评价的工具。对于某个二态分类预报对象,用实况对站点或格点的预报结果进行检验,其结果可构成如表 3的二态事件预报与实况表。
|
|
表 3 二态事件预报与实况表 |
其中A为预报发生准确数 (指站点或格点数或总次数),B为空报数,C为漏报数,D为预报不发生准确数。用HR代表命中率、FAR代表假警报率,则:

|
用一系列不同的概率作为预报对象发生的概率临界值,可得到一系列不同的命中率和假警报率,用命中率作为纵坐标、假警报率作为横坐标绘制的曲线即为ROC曲线。
若以0 %作为概率临界值,即预报对象总是发生,则HR=1,FAR=1;若以100 %作为概率临界值,即预报对象总是不发生,则HR=0,FAR=0。经过 (0,0) 和 (1,1) 两点的直线 (即对角线) 是概率预报是否有技巧的分界线。当ROC曲线位于该对角线上方时为有技巧预报,此时ROC曲线下方的面积 (称为ROC面积)>0.5;当ROC曲线位于该对角线下方时为无技巧预报,此时ROC面积<0.5;概率预报最佳时,HR=1,FAR=0,此时ROC面积=1。
仍将降水分成小雨—大暴雨等5个量级,分别绘制各个例在2039个站点上24 h发生各量级以上降水的ROC曲线以及22个个例的平均ROC曲线,当某个例发生某量级以上降水的站点小于3个时,则不再绘制该个例发生该量级以上降水的ROC曲线,平均ROC曲线也不再包含该个例的结果。这里分别以从0 %至100 %、间隔10 %的11个概率值作为概率临界值。
5 试验结果 5.1 RPS评分表 4给出了24 h降水概率预报的RPS评分。显然三种方法中Rank法的预报效果最好,相关法的预报效果与平均法基本相同。Rank法的RPS评分一般小于平均法10 %以上,前24 h差异最大的为个例11,达到24.2 %,差异最小的个例14也有8.4 %;后24 h差异最大和最小的分别为个例10的23.7 %和个例2的8.8 %;前24 h和后24 h的平均差异分别为15.8 %和17.2 %。比较相关法与平均法的RPS评分,虽然前24 h有5个个例、后24 h有12个个例相关法的RPS评分小于平均法,但差异都只有0.001,不足1 %。
|
|
表 4 24 h降水概率预报的RPS评分 |
从表中结果还可以看到,无论哪一种方法,RPS评分大的个例往往降水范围广、强度大。如前24 h 22个个例中RPS评分最大的个例20是这些个例中降水强度和范围最大的,后24 h RPS评分最大的个例11也是降水强度和范围较大的,其原因一方面与预报能力有关,降水强度越大预报能力往往越低,另一方面与统计方法有关,这里给出的RPS评分是预报区域内2039个站点的平均RPS值,当一大片区域没有发生降水时,预报其发生降水的概率往往较低,当发生降水尤其强度大的降水时,预报的降水概率则不一定高,这样前者的RPS值往往小于后者,因此当降水范围广时,区域平均的RPS评分往往也较大。此外,前24 h的平均预报效果好于后24 h,这主要也是由于大部分个例前24 h的降水强度和范围比后24 h小的缘故。
5.2 BS评分RPS评分是对所有量级降水的概率预报结果进行综合评价的指标,这里分别考察各个量级降水的概率预报效果。表 5给出了前24 h发生小雨、中雨和大雨以上降水概率预报的BS评分。
|
|
表 5 0~24 h降水概率预报的BS评分 |
表中结果显示,对小雨以上降水的概率预报,Rank法的预报效果明显好于平均法和相关法,Rank法的BS评分小于平均法的幅度,除了个例12为7.5 %以外,其余的都在10 %以上,有3个个例在20 %以上,平均为16 %。对中雨以上降水的概率预报与对小雨以上降水的概率预报既相似又有区别,区别在于对于不同个例,三种方法中效果最好的Rank法的BS评分小于平均法的幅度有很大差别,最大的达到27.3 %,最小的只有3 %,大于20 %的有7个个例,小于10 %的也有5个个例,平均幅度为16.7 %,则与对小雨以上降水的概率预报结果接近。
随着降水量级的增大,以上的这种区别更为显著。对大雨以上降水的概率预报,虽然Rank法的平均BS评分比平均法小13.3 %,但有8个个例两者相同,在Rank法的BS评分小于平均法的14个个例中,最大差异达到34.6 %。对暴雨以上降水的概率预报 (结果略),只有6个个例Rank法的BS评分小于平均法,其余的除了两者相同外,还有3个个例Rank法的BS评分大于平均法,尽管如此,Rank法的平均BS评分小于平均法的幅度仍高达25 %。而对大暴雨以上降水的概率预报 (结果略),所有个例三种方法的BS评分都相同,由于发生大暴雨的个例很少,即使发生大暴雨,其范围也很小,因此这一结果不具有普遍性。
比较相关法和平均法的预报,对小雨以上降水的概率预报,除了5个个例相关法的BS评分比平均法小0.001外,其余的都相同,对中雨和大雨以上降水的概率预报,分别只有一个个例两种方法的BS评分有0.001的差异,对暴雨以上降水的概率预报 (结果略),所有试验个例两种方法的BS评分都相同。
总的说来,对各量级以上降水的概率预报,平均而言,Rank法的预报效果是三种方法中最好的,相关法的预报效果和平均法相同。随着降水量级的增大,对不同个例,Rank法的预报效果好于平均法的程度有很大差别,有时可能相同,有时也可能比平均法差。后24 h的结果 (略) 与前24 h相似。
从表中结果还可以看到,降水量级越大,BS评分越小,这主要与统计方法有关,并非表明对量级大的降水的概率预报效果好于对量级小的降水的概率预报效果。这里参加评价的站点是固定不变的,降水范围的大小则是变化的,量级小的降水范围总比量级大的降水范围大,而降水范围大的BS评分一般要比降水范围小的BS评分大,其原因与前面分析的原因相同,因此这里不同量级降水的BS评分不具有可比性。同样,对相同量级的降水,降水范围大时,其BS评分往往也大,因此不同个例的BS评分也没有绝对的可比性。
5.3 ROC曲线ROC曲线反映的也是某个量级降水的概率预报状况。图 1为前24 h发生小雨 (0.1mm)、中雨 (10 mm)、大雨 (25 mm) 和暴雨 (50 mm) 以上降水的平均ROC曲线,其中发生暴雨以上降水的平均ROC曲线为12个个例的平均。由于发生大暴雨以上降水的平均ROC曲线仅为一个个例的结果,这里不再给出这一结果。

|
|
| 图 1. 0~24 h发生小雨 (a)、中雨 (b)、大雨 (c) 和暴雨以上 (d) 降水的平均ROC曲线 (平均法:直线, 相关法:短虚线, Rank法:长虚线) | |
从图中可以看到,无论小雨、中雨、大雨还是暴雨,相关法和平均法的ROC曲线重合,表明对各量级以上降水的概率预报,两种方法的平均预报效果相同,这与BS的结果是一致的;Rank法的平均预报效果则要好于平均法和相关法,但其好于平均法和相关法的幅度很小,表现在图中Rank法的ROC曲线虽然位于平均法和相关法的上方,但非常接近,尤其对中雨和大雨,这一点与BS结果有所不同,BS评分显示Rank法好于平均法和相关法的幅度平均都在10 %以上,甚至达到25 %。这主要与评价方法有关,虽然BS评分和ROC曲线都是对某个等级的概率预报结果进行评价的工具,但前者统计的是预报概率的均方误差,后者统计的则是命中率和假警报率的大小,而预报对象发生的概率临界值是随机的,两种评价方法的侧重点不同导致了结果的差异。后24 h的预报结果 (图略) 与前24 h相似。
从图中还可以看到,无论小雨、中雨、大雨还是暴雨,三种方法的ROC曲线都位于对角线上方,即ROC面积>0.5,但随着降水量级的增大ROC面积逐渐减小,表明平均而言,三种方法对各量级以上降水的概率预报都是有技巧预报,即命中率高而假警报率低,对量级小的降水的概率预报技巧要高于对量级大的降水的概率预报技巧。后24 h的预报结果 (图略) 也如此。
6 结论本文以MM5模式作为试验模式,通过选取不同的物理过程参数化方案产生8个集合成员,分别用平均法、相关法和Rank法对非汛期22个降水个例进行短期集合降水概率预报试验。结果显示:
(1) 考察小雨—大暴雨6类降水的概率预报的综合预报效果:所有试验个例Rank法的预报效果都明显优于平均法和相关法,Rank法好于平均法的平均幅度在15 %以上;相关法的预报效果和平均法基本相同,除了部分个例两种方法的预报效果有不足1 %的差异外,其余的两者都相同。
(2) 从均方误差角度分别考察发生小雨、中雨、大雨和暴雨以上降水的概率预报效果:对各量级以上降水的概率预报,Rank法的平均预报效果是三种方法中最好的,Rank法好于平均法的平均幅度在10 %以上;随着降水量级的增大,相对于平均法,Rank法的预报效果呈现不稳定状态,有些个例Rank法的预报效果与平均法相同,个别个例Rank法的预报效果可能比平均法差;对于相关法和平均法,两种方法的预报效果基本相同,对量级大的降水的概率预报,几乎所有个例两种方法的预报效果都相同。
(3) 从命中率和假警报率的相对大小角度分别考察发生小雨、中雨、大雨和暴雨以上降水的概率预报效果:对各量级以上降水的概率预报,相关法的平均预报效果与平均法相同,Rank法的平均预报效果好于平均法和相关法,但Rank法好于平均法和相关法的幅度很小,尤其对中雨和大雨以上降水的概率预报。
(4) 平均而言,平均法、相关法和Rank法对各量级以上降水的概率预报都是有技巧预报,对量级小的降水的概率预报技巧高于对量级大的降水的概率预报技巧。
如何从所有集合成员结果中提取有用信息得到概率预报,针对降水概率预报的试验表明,集合与统计相结合的Rank法是一种有效的方法。同样将集合与统计结合的相关法的预报效果要差一些,与简单的平均法相同,这是否与进行相关分析时,没有将区域内不同站点分开统计有关?事实上对不同站点、尤其距离较远的站点,集合成员的预报与实况间的相关性是不同的。如果积累足够多的集合预报结果,进行相关分析时将不同站点分开统计或将整个区域划分为若干个小区域进行统计,预报结果是否会有所改进?对于Rank法,在确定其等级分布时也用同样方法处理,预报结果是否会更好一些?这些都需要继续试验。
| [1] | Lorenz E N, Deterministic nonperiodic flow. J Atmos Sci, 1963, 20: 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [2] | Toth Z, Kalnay E, Ensemble forecasting at NCEP and the breeding method. Mon Wea Rev, 1997, 125: 3297–3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
| [3] | Hersbach H, Mureau R, Opsteegh J D, et al. A short-range ensemble predictionsystem for the European area. Mon Wea Rev, 2000, 128: 3501–3519. DOI:10.1175/1520-0493(2000)128<3501:ASRTEM>2.0.CO;2 |
| [4] | Mullen S L, Buizza R, Quantitative precipitation forecasts over the United States by the ECMWF ensemble prediction system. Mon Wea Rev, 2001, 129: 638–663. DOI:10.1175/1520-0493(2001)129<0638:QPFOTU>2.0.CO;2 |
| [5] | Wandishin M S, Mullen S L, Stensrud D J, et al. Evaluation of a short-range multimodel ensemble system. Mon Wea Rev, 2001, 129: 729–747. DOI:10.1175/1520-0493(2001)129<0729:EOASRM>2.0.CO;2 |
| [6] | Du J, Mullen S L, Sanders F, Short-range ensemble forecasting (SREF) of quantitative precipitation. Mon Wea Rev, 1997, 125: 2427–2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
| [7] | Stensrud D J, Bao J W, Warner T T, Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems. Mon Wea Rev, 2000, 128: 2077–2107. DOI:10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2 |
| [8] | Ebert E E, Ability of a poor man's ensemble to predict the probability and distribution of precipitation. Mon Wea Rev, 2001, 129: 2461–2480. DOI:10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2 |
| [9] | Hamill T M, Colucci S J, Evaluation of Eta-RSM ensemble probabilistic precipitation forecasts. Mon Wea Rev, 1998, 126: 711–724. DOI:10.1175/1520-0493(1998)126<0711:EOEREP>2.0.CO;2 |
| [10] | Hamill T M, Colucci S J, Verification of Eta-RSM short-range ensemble forecasts. Mon Wea Rev, 1997, 125: 1312–1327. DOI:10.1175/1520-0493(1997)125<1312:VOERSR>2.0.CO;2 |
 2005, 16 (1): 78-88
2005, 16 (1): 78-88






