引用本文

胡邦辉, 谭言科, 王举. 热带气旋海面最大风速半径的计算[J]. 应用气象学报, 2004, 15(4): 427-435.

Hu Bang hui, Tan Yanke, Wang Ju.
CALCULATION OF MAXIMUM WIND VELOCITY RADIUS OF TROPICAL CYCLONE ON SEA SURFACE[J]. Journal of Applied Meteorological Science, 2004, 15(4): 427-435

热带气旋海面最大风速半径的计算
2003-02-28 收到, 2003-09-19 收到修改稿.
摘要: 利用含有摩擦的平面极坐标水平运动方程组, 引入藤田气压模式, 在热带气旋域内最大风速为已知的条件下, 经过合理的简化和推导, 得到了呈稳定状态的海面移动非对称热带气旋的最大风速半径的计算方案。分析结果表明, 当最大风速越小、中心气压越低、环境温度和气压越高、纬度越低或摩擦系数越小时, 热带气旋的最大风速半径就越大;反之, 最大风速半径就越小。最大风速和它半径上的最小风向内偏角出现在热带气旋移向的右后侧。对9109号和9115号热带气旋的计算表明, 最大风速半径在发展初期增加, 在发展后期减小, 而在衰减期迅速增加。
关键词:
热带气旋 最大风速半径 非对称结构
CALCULATION OF MAXIMUM WIND VELOCITY RADIUS OF TROPICAL CYCLONE ON SEA SURFACE
Hu Bang hui,
Tan Yanke,
Wang Ju
Institute of Meteorology , PLA University of Science & Technology , Nanjing 211101
Abstract:
By the agency of Fujita pressure formula, a method to calculate the maximum wind velocity radius of mobile asymmetric tropical cyclone (TC) over the sea in the circumstance that the strength keeps constant is developed in terms of the horizontal momentum equations with frictions in the polar coordinates after the reasonable simplification and derivation in the presence of the maximum wind speed. The result suggests that the maximum wind velocity radius will be large under the conditions that the maximum wind is small, the central pressure is low, the environmental air temperature and pressure are high, and the TC locates at a the low latitude or the friction coefficient is small, and vice versa. The maximum wind speed with minimum inner deflection angle resides at the right back side of the TC moving direction. The case studies of 9109 and 9115 TC indicate that the maximum wind radius increases in the initial stage of the TC development, decreases in the mature period, and enhances rapidly in the decay phase.
Key words:
Tropical cyclone
Maximum wind speed radius
Asymmetrical structure
引言 热带气旋风场是气象工作者预报热带气旋引起的大风、海浪和风暴潮等恶劣天气时常常需要计算的物理量。常用的计算方法有:藤田 (1952年) 提出的藤田公式[1]和美国气象局水文气象部 (1954年) 提出的Myers公式[2]等。这些圆对称气压模式的应用效果表明它们能基本反应热带气旋域内实际气压的分布。例如, 房文鸾等[3]用热带气旋的摩擦梯度风场与移动风场合成, 提出了适合东海热带气旋的风速分布计算方案。但是, 圆对称气压模式与热带气旋的最大风速半径有关, 在使用时该因子一般被取为常数, 这与实际情况有较大的偏差。为此, 陈孔沫[4]用一根热带气旋外围的等压线替代难以确定的最大风速半径, 可以避免使用最大风速半径产生的误差, 只是外围等压线预报场位置的确定还较为复杂。同样, 这种圆形对称涡旋还应用到了数值预报的人造台风之中, 即人为地在初始场中构造一个标准台风模型, 并加进某种可表征台风及其环境气流运动的非对称分量[5, 6]。其实, 许多观测事实和研究成果都表明台风的结构具有明显的非对称特征[7~10], 而包含了轴对称台风的数值模式常常有某种系统性偏差[11]。其中, 无论是在计算台风大风还是在构造人造台风时, 热带气旋最大风速半径是一个重要而复杂的因子, 尤其是非对称台风各个方向上的最大风速半径。本文将提出一种适合于海面非对称热带气旋最大风速半径的计算公式。
1 热带气旋海面最大风速半径的计算 以热带气旋中心为原点, 考虑海面摩擦的热带气旋域内任意一空气质点的平面极坐标水平运动方程组为[12]
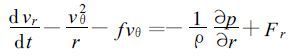
|
(1) |
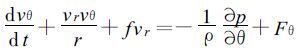
|
(2) |
以上两式中的Fr和Fθ分别为r方向和θ方向的摩擦力, 可以假定热带气旋呈稳定状态[13], 即dvr/dt=0,dvθ/dt=0, 得
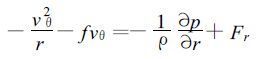
|
(3) |
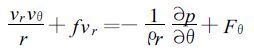
|
(4) |
当热带气旋以速度vs移动时, 在域内任意一点处, 静止热带气旋的曲率半径r′与移动热带气旋的曲率半径r存在如下关系[12]
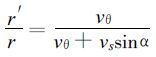
|
(5) |
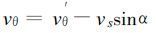
|
(6) |
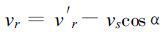
|
(7) |
以上三式中, α为热带气旋的移动方向与所讨论点到气旋中心连线的夹角, 规定逆时针方向为正, v′θ和v′r分别是静止热带气旋的切向和径向速度; 同样, vθ和v r分别是移动热带气旋的切向和径向速度, 根据文献[14]可以将式 (5) 中的热带气旋移动对曲率半径r的影响在控制方程式 (3) 和式 (4) 中的惯性项中得到考虑, 有
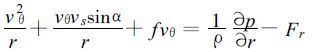
|
(8) |
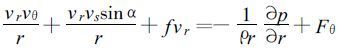
|
(9) |
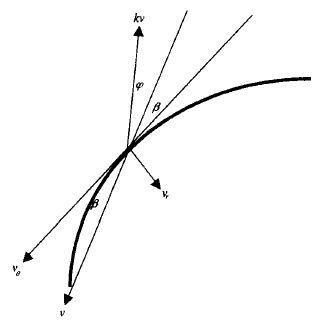
取圆对称气压场, 令摩擦系数为k, 且海面摩擦力可以粗略地表示为kv, 实际风向等压线内侧偏离的角度为β[14], 参看图1, 存在如下关系
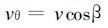
|
(10) |
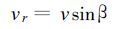
|
(11) |
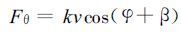
|
(12) |
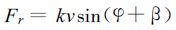
|
(13) |
以上两式中φ代表摩擦阻力偏离实际风矢量反方向的夹角, β称为风向内偏角。将式 (10) ~(13) 代入式 (8) 和式 (9) , 有
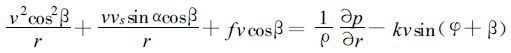
|
(14) |
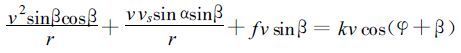
|
(15) |
取热带气旋域内圆对称气压模式由藤田公式决定, 那么域内任意一空气质点处的气压和气压的变化为:
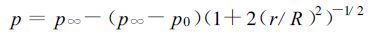
|
(16) |
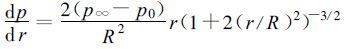
|
(17) |
以上二式中p0为热带气旋的中心气压, 它与所讨论点的半径r和方位角θ无关。p ∞和R分别是环境气压和最大风速半径, 它们都只与θ有关, 而与r无关。在圆形气压场域内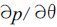 =0, 取讨论点处于最大风速点处, 即r等于R, 从式 (16) 和 (17) 得到最大风速半径处的气压和气压的变化:
=0, 取讨论点处于最大风速点处, 即r等于R, 从式 (16) 和 (17) 得到最大风速半径处的气压和气压的变化:
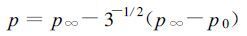
|
(18) |
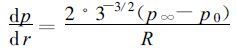
|
(19) |
将状态方程代入式 (14) , 替换空气密度ρ, 并令
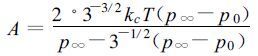
|
(20) |
上式中kc代表气体常数, T代表海面气温, 将上式代入式 (14) , 当讨论点处于最大风速vα点处时, 式 (14) 和式 (15) 有r等于R, 表示如下:
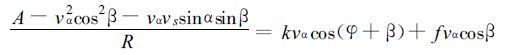
|
(21) |
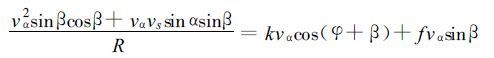
|
(22) |
假定最大风速vα已知, 热带气旋静止时, vs等于零, 求解以上两式, 静止热带气旋的风向内偏角β和最大风速半径R的计算公式表示如下:
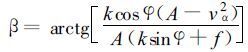
|
(23) |
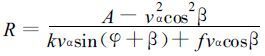
|
(24) |
当热带气旋移动时, 消去式 (21) 和 (22) 中的R, 得
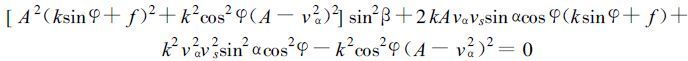
|
(25) |
令
将以上三式代入式 (25) , 有以下解
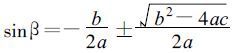
|
(26) |
取式 (26) 的正解, 将它代入式 (21) , 移动热带气旋的风向内偏角β和最大风速半径R的计算公式表示如下:
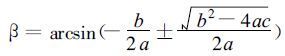
|
(27) |
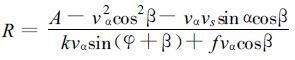
|
(28) |
2 热带气旋最大风速和最大风速半径的影响参数
2.1 最大风速 热带气旋任意方位α上的最大风速vα由最大环流风速vmaxc和移动风速vs两部分组成。最大环流风速与方向无关, 即静止热带气旋任意方位α上的最大风速是相等的; 移动热带气旋最大风速v随方位α的不同而变化。在移动热带气旋随方位α变化的任意最大风速vα中, 其最大的vα表示为vmax, 假定为已知, 且方向与移动方向相同, 那么环流风速最大值可表示为:
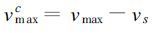
|
(29) |
任意方位α的最大风速v可表示为:
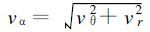
|
(30) |
其中
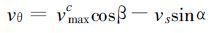
|
(31) |
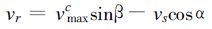
|
(32) |
2.2 最大风速半径和影响参数 由式 (28) , 影响热带气旋最大风速半径的参数有:中心气压p0、外围环境气压p∞、最大风速vα、摩擦系数k、环境温度T、摩擦阻力偏离实际风矢量反方向的夹角φ和纬度等, 以下将讨论这些参数对最大风速半径的影响。
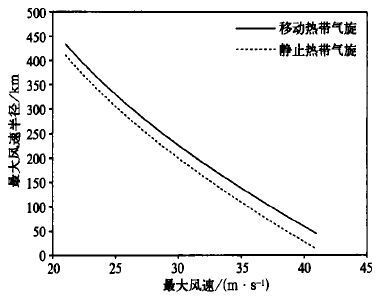
图2给出了海面移动热带气旋长轴和静止热带气旋的最大风速半径与最大风速之间的关系, 图中可见, 移动或静止热带气旋的最大风速半径都随着最大风速的增大而减小。假定有两个仅最大风速不同而其它影响参数相同的热带气旋, 最大风速处的空气质点与热带气旋中心的距离将在最大风速大的热带气旋中较近, 而在最大风速小的热带气旋中较远。同理, 在一个最大风速随方位α变化而其它影响参数相同的热带气旋中, 最大风速处的空气质点与热带气旋中心的距离在最大风速相对大的方位上较近; 在最大风速小的方位上较远。
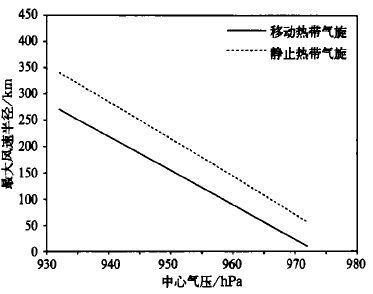
图3是海面移动和静止热带气旋最大风速半径与中心气压之间的关系, 可以看出, 最大风速半径随热带气旋中心气压的降低而增大。对于中心气压不同而其它影响参数相同的热带气旋, 强热带气旋产生的大风分布范围要比弱的产生的要大。
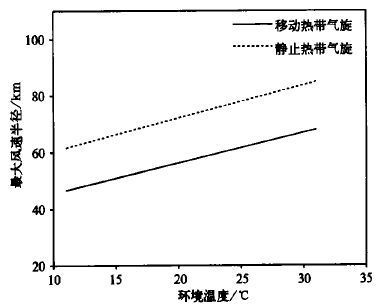
图4是海面移动和静止热带气旋最大风速半径与环境温度之间的关系, 图中的最大风速半径随环境温度的增大而增大, 表明最大风速半径的大小与热带气旋发生的季节有关, 强度相同的热带气旋在环境温度高的季节的最大风速半径要比在环境温度低的季节大, 在夏季要比在春秋两季要大; 同一热带气旋在环境温度高的空气质点的最大风速半径要比温度低的质点的相对要大。经计算, 移动和静止热带气旋的最大风速半径都随环境气压p∞的增加而增大 (图略), 当考虑副热带高压或赤道高压等系统影响时, 靠近它们一侧的热带气旋的空气质点的最大风速半径要比远离它们一侧的要大。热带气旋的最大风速半径与所处纬度有明显关系, 随纬度的增加而减小 (图略), 强度不变的热带气旋在北上过程中, 其最大风速半径会逐渐减小。摩擦阻力F是一个重要的影响因子, 体现在摩擦系数k的变化和摩擦阻力偏离实际风矢量反方向的夹角φ的选取上, 热带气旋的最大风速半径随摩擦系数k的增大而迅速减小 (图略), 表明相同强度的热带气旋在陆地上的最大风速半径要远远小于在海面上的最大风速半径, 本文取摩擦系数k等于2×10-4, φ等于38°[14]。
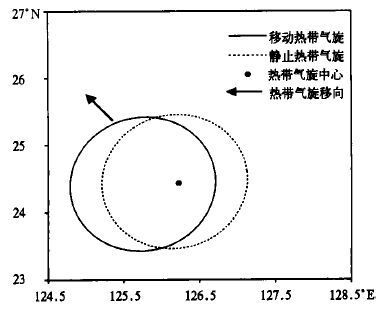
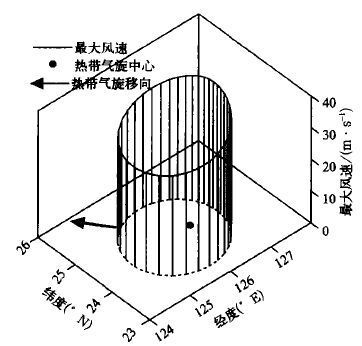
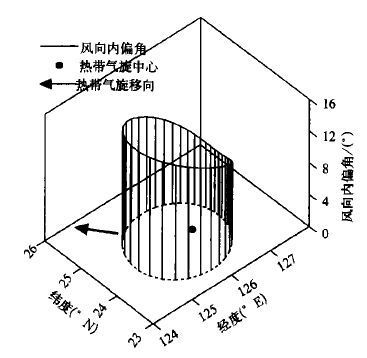
2.3 非对称最大风速半径与热带气旋的移动和风向内偏角 静止热带气旋任意方位α上的最大风速vα由最大环流风速决定, 在其它影响参数相同时, 从图5可以看到, 其任意方位α最大风速半径呈一个以热带气旋为中心的圆, 这种圆对称分布表明最大风速半径与方位角α无关。当热带气旋以速度vs沿图5中箭头所示方向移动时, 如果不考虑副热带高压等系统对环境气压p∞的影响, 则最大风速呈现一种非对称分布, 与方位角α有关。因此, 热带气旋的移动是引起最大风速半径呈非对称分布的主要影响参数之一。最大风速半径的非对称分布与最大风速的非对称分布有关 (图6), 随方位α变化的任意最大风速vα中, 其最大的vα出现在热带气旋移向的右后侧, 这与观测到的实际热带气旋的大风分布一致。由最大风速半径与最大风速之间的关系可知, 风速愈大, 风速半径愈小 (其它影响参数不变), 因此, 热带气旋中的最大风速出现在风速半径最小处。图7是移动热带气旋任意方位α上的风向内偏角与最大风速半径的对应关系, 从图1可知风速切向分量愈大, 风向内偏角愈小, 从图7中可见, 热带气旋中的最大风速出现处, 风向内偏角最小。
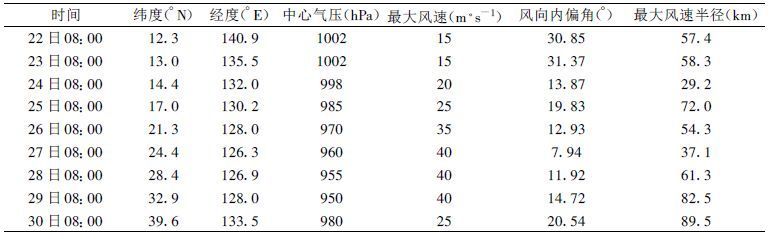
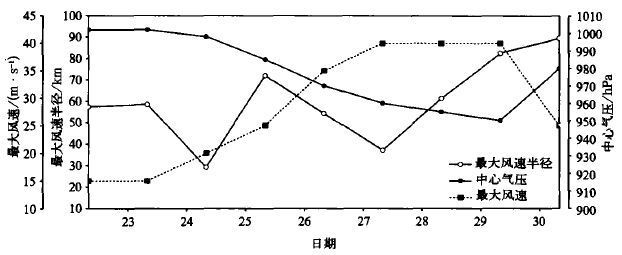
3 个例分析 为了分析热带气旋的最大风速半径的变化, 本文给出了两个实际个例。表1和图8是9109号热带气旋的最大风速半径及其影响因子的逐日演变。假定环境气压和环境温度等因子不变, 可以看出, 初生期 (7月22日08 :00至24日08 :00) 最大风速半径较小, 有一次降低过程, 过程中中心气压降幅不大 (4 hPa), 最大风速增幅有5 m·s-1, 纬度增加2.1°, 表明第一个影响参数的作用与后两个影响参数的相反, 后两个影响参数的贡献大于第一个影响参数的贡献。发展期初期 (24日08 :00至26日08 :00) 最大风速半径增大, 期间中心气压降低28 hPa, 最大风速增加15 m·s-1, 纬度增加6.9°, 第一个影响参数的贡献大于后两个影响参数的贡献; 发展期后期 (26日08 :00至27日08 :00) 最大风速半径又一次减小, 中心气压降幅为10 hPa, 最大风速增加5 m·s-1, 纬度增加3.1°, 后两个影响参数的贡献占优势。成熟期 (27日08 :00至29日08 :00) , 中心气压降幅为20 hPa, 最大风速不变, 纬度增加3.1°, 中心气压降低的贡献占优势。衰减期 (29日08 :00至30日08 : 00) 中心气压升高和纬度增加有负贡献, 最大风速减小有正贡献, 由于风速衰减的作用大, 使得最大风速半径增加。过程中风向内偏角的变化趋势与最大风速半径的一致, 即半径小它也小, 半径大它也大。同理, 可以分析表2及示意图 (图略) 所反映的9115号热带气旋的最大风速半径与诸影响参数的演变。一般而言, 发展期初期中心气压的迅速降低会使最大风速半径有一个增加的过程, 发展期后期中心最大风速的迅速增加会使最大风速半径有一个减小的过程, 衰减期最大风速的衰减使半径有一个迅速增加的过程。
表 1

表 1 9109号 (7月) 热带气旋逐日最大风速半径变化 (α=243°)
|
表 1 9109号 (7月) 热带气旋逐日最大风速半径变化 (α=243°)
|
表 2

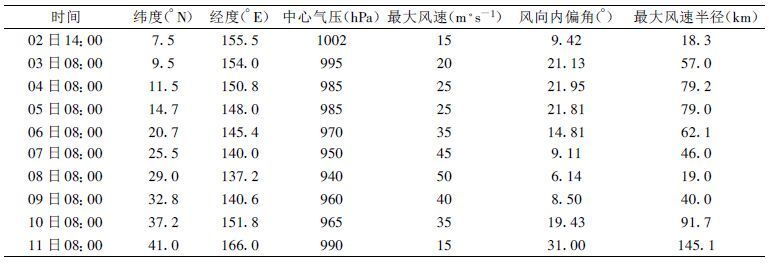
表 2 9115号 (9月) 热带气旋逐日最大风速半径变化 (α=243°)
|
表 2 9115号 (9月) 热带气旋逐日最大风速半径变化 (α=243°)
|
4 结论 (1) 利用含有摩擦的平面极坐标水平运动方程组, 引入藤田气压模式, 在热带气旋域内最大风速为已知的条件下, 经过合理的简化和推导, 得到了呈稳定状态的海面移动非对称热带气旋的最大风速半径的计算方案。
(2) 经过对热带气旋最大风速半径的影响参数的讨论, 认为气压梯度 (中心气压p0、外围环境气压p∞)、最大风速vα和摩擦力 (摩擦系数k) 对热带气旋最大风速半径的大小起主要作用; 环境温度T、摩擦阻力偏离实际风矢量反方向的夹角φ和纬度等也有一定作用。当最大风速越小、中心气压越低、环境温度和气压越高、纬度越低或摩擦系数越小时, 热带气旋的最大风速半径就越大; 反之, 最大风速半径就越小。
(3) 对移动热带气旋的计算表明, 最大风速和它半径上的最小风向内偏角出现在热带气旋移向的右后侧; 除了非对称的环境气压p∞, 热带气旋的移动参数也对最大风速半径呈非对称分布起主要作用。
(4) 对9109号和9115号热带气旋的计算表明, 最大风速半径和风向内偏角的计算公式能够反映处于不同阶段热带气旋的相应特征, 最大风速半径在发展初期增加, 在发展后期减小, 而在衰减期迅速增加。
在我们早期的工作中, 我们已经将本文中的方法用于热带气旋域内风场分布的计算之中, 将8706号和9104号热带气旋的计算风场和观测风场进行比较, 结果表明它们是非常一致的[15], 这说明本文提出的热带气旋最大风速半径的计算方案是合理的, 具有重要的应用价值。
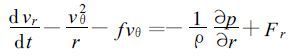
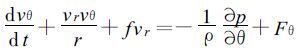
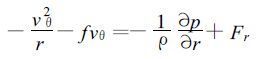
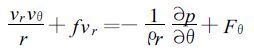
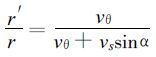
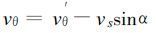
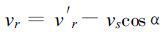
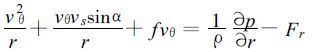
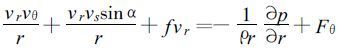
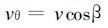
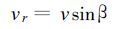
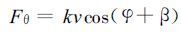
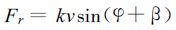
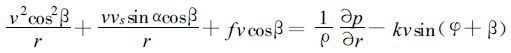
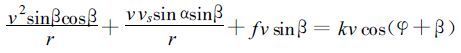
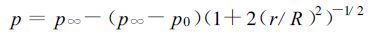
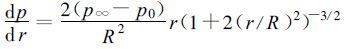
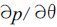
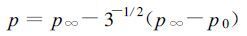
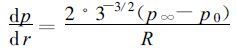
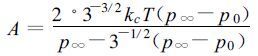
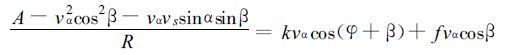
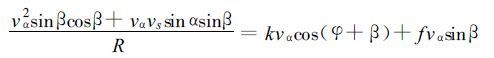
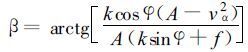
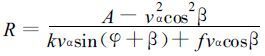
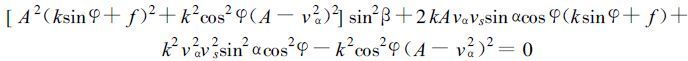
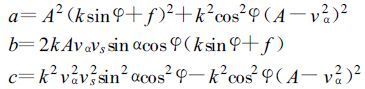
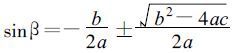
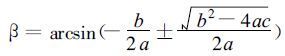
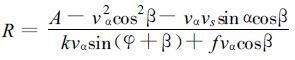
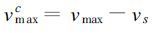
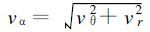
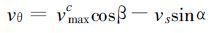
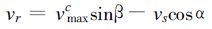
 2004, 15 (4): 427-435
2004, 15 (4): 427-435