2. 中国科学院大气物理研究所, 北京 100029;
3. 中国气象局, 北京 100081
2. Institute of Atmospheric Physics , Chinese Academy of Sciences , Beijing 100029;
3. China Meteorology Administration , Beijing 100081
数值天气预报是对计算机资源要求最迫切的领域之一。近年来采用分布式内存的并行机得到了迅猛的发展,可达到比传统向量并行机高得多的运算速度。如欧洲中期预报中心数值预报业务在模式分辨率方面,已经增加到了T511,并且还在继续增加; 在数值积分格式方面采用了半拉格朗日方法和约化格点,大大提高了数值积分格式的效率; 在并行计算方法上采用了消息传递方式,可以在多达数百甚至一千个处理结点组成的分布式内存并行计算机上运行。
可以看出,应选择合适的算法并且在最有效率的计算机上运算。目前在数值天气预报中,采用了半拉格朗日方法 (S Laggian) 处理模式的平流项[1~3],能使时间步长加大,时间截断误差与空间截断误差相适应,具有很好的效果。我国有学者做了这个方面的工作[4~7],另外,国内较早对并行数值计算开展了研究[7~9],国家气象中心从20世纪90年代中期开始研究在并行计算机上应用数值预报模式的问题[10~14],①,但还未有针对半拉格朗日方法的并行算法研究。因此,研究半拉格朗日方法的并行问题是必要的,有意义的。
① 金之雁, 丁小良, 颜宏.并行计算数值天气预报模式.第四届全国并行计算会议文集.全国并行计算学术交流会组织委员会, 1993 。
本文重点研究的问题是分布式并行计算机消息传递方式下半拉格朗日并行算法问题。具体在SP2并行计算机MPI (Message Passing Interface) 消息传递环境下实现。二维浅水波并行模式中采用区域分解法,通过试验对模式的并行效率进行了一系列对比分析研究。为今后在更复杂的天气预报业务模式的应用提供可借鉴的方法和技术。
1 试验模式的基本结构 1.1 半拉格朗日法的原理简介描写流体运动的两种方法,一种是欧拉法,即在空间的固定位置观察流体的运动变化; 另一种是半拉格朗日法,指在同一积分过程中不对同一气块沿其路径追踪,而是在同一时间步长内追踪终点总是在网格点上的气块。半拉格朗日法有突出的优点,如物理意义明确,易避免非线性不稳定,计算稳定,可突破CFL条件限制。使用大时间步长,从而提高计算效率,计算位相速度较好等。缺点是在地形陡峭的地区歪曲较大等,大的时间步长很难描述生命史短的物理过程,只能采用参数化方法等。
为了说明半拉格朗日格式的基本思想,考虑一维平流方程:
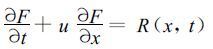
|
(1) |
其中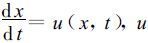
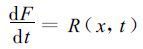
|
(2) |
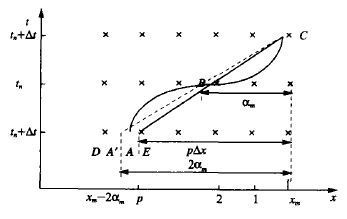
如图 1所示,一流体质点经过一定时间间隔,如两倍时间步长2Δt后,由出发点A (不一定位于规则网格点上) 到达规则格点C。一般这是一条曲线。半拉格朗日格式就是研究这类经1或2个时间步长后到达规则网格点的运动。
1.2 Ritchie[15]非内插格式图 1中,最靠近出发点A′的规则网格点E,它距到达点C为p个格距,这样E点到C点的距离就为p ΔX,其中ΔX是格距。p由以下公式求得:
|
|
| 图 1. 三时间层半拉格朗日格式示意图 (实曲线CA为流体质点的实际轨迹。长虚线CA′为一般内插格式的近似轨迹,实直线CE为RITCHIE非内插格式的近似轨迹。D,E位于格点上。B为CA′的中点。质点在tn +Δt时位于xm。αm为质点在Δt时间所走的距离) | |
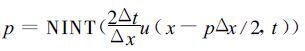
|
(3) |
其中NINT表示取最近的整数。通过在平流风速上加减p ΔX /2ΔT项,就可将方程中的平流项分为两个部分,一部分为半拉格朗日平流,另一部分为剩余平流。平流风速可写为:
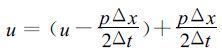
|
(4) |
令: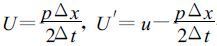
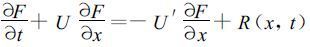
|
(5) |
式中右端第一项即剩余平流项。方程的左端表示,流体质点以速度U=p Δx/Δt移动时标量F的总体微分,此流体质点在过去2Δt内经过了p个格距。写成总体微分形式,
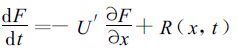
|
(6) |
应用中央差分,方程可写为如下形式:
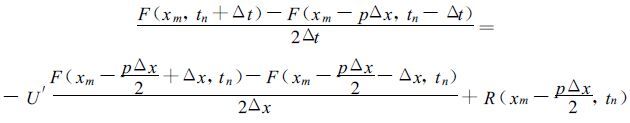
|
(7) |
上式中,当p为偶数时,I′点 (xm-p Δx/2) 和O′点 (xm-pΔx) 就都在规则网格点上。显然,在O′点和I′点就回避了一次内插; 当p为奇数时,O′点 (xm-pΔx) 在规则网格点上,I′点 (xm-pΔx /2) 不在规则网格点上,但I′点的内插十分简单,在两个格点的中点。对于二维情况也仅有三种可能:在X或Y方向两个格点的中点,或在网格对角线的交点上。
1.3 浅水波方程模式浅水波方程模式的两个基本假定:(1) 假定大气是均匀不可压缩的流体; (2) 水平风速不随高度变化,基本含义是水平运动和高度无关。浅水波方程模式仍满足质量守恒,能量守恒,位涡度守恒,位涡拟能守恒等性质。浅水波方程模式作为气象问题算法检验模式,一直被人们采用。我们考虑如下形式的浅水波方程组:
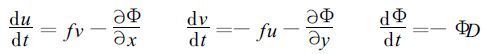
|
(8) |
其中,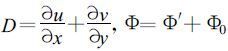
将Ritchie非内插格式应用于方程组 (8),可得类似于 (7) 的方程:
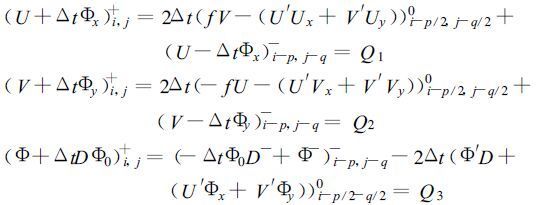
|
(9) |
其中,U′,V′定义如下:
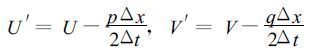
|
(10) |
整理得赫姆霍兹方程:
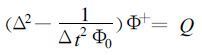
|
(11) |
其中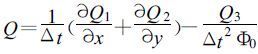
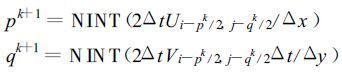
|
(12) |
其中,k为迭代次数。
1.4 对比方案及初始场介绍由于对初始场随时间的积分无法用准确的解析解来表示,故采用差分格式的浅水波模式,本文采用Shumann [16]格式。对初始场进行积分,将此模式运算结果与半拉格朗日方法的结果进行比较,来检验半拉格朗日方法的效果。该模式的离散网格与半拉格朗日模式所使用的相同,空间差分使用Shumann格式,时间积分起步用向前差,然后用中央差。取南北边界为刚壁,东西为周期边界条件的槽形区域。初始场为理想场,初始高度场给定,由地转近似求出风场。描述沿着环状区域不同波长和振幅的有着南北扰动的西风气流 (本文取4波)。初始高度场公式为:
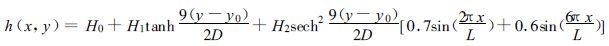
|
(13) |
其中,L为环带长,D为环带宽。y0=D/2为此环带的中线。
2 并行浅水波模式的区域分解法及HALO的初步研究 2.1 并行计算环境本文所使用的32个结点的SP2并行计算机是分布式内存并行计算机,并行计算模式为消息传递MPI (Messgae Passing Interface) 模式,是指一组有局地内存的处理机之间,通过消息传递的送和收来进行通讯,在数据传输中要求每个处理机进行合作。
2.2 本文模式的并行方法 (区域分解法)将单CPU上编写的串行模式在MPI环境下采用分区域并行计算方法并行化。
2.2.1 区域划分将整个计算区域按照在X方向和Y方向所提供的结点个数分成若干子区域,将这些子区域分别交给不同的结点同时运算,每个结点只负责本子区域内部格点的计算。这样,通过若干结点同时运算,减少预报完成的时间。给定总结点数的划分方式之后,结点之间的相对位置就可以确定。
2.2.2 消息传递模式采用Fortran程序中调用消息通讯库MPI和数据并行的办法。不同结点使用的是与在单结点上相同的Fortran程序,但是在执行时,不同结点上的循环参量,数组大小,消息传递数据交换子程序等有微小不同。这是根据结点在整个预报区域的位置决定的。在程序中,所有代表独立变量的大数组被分为局部小数组,分配给每个结点。这些局部数组在四边有额外的行和列。这些额外的行和列用来存放此结点周围相邻结点内边界附近格点的值,这是因为这些子区域内部边界附近的格点,在每一时间步长内空间差分及找出发点时,用到了相邻区域的格点值。这些格点存放在相应相邻结点的内存中,在使用时,通过结点间的消息传递得到。当时间积分结束后,各个结点将最后结果送到指定的结点上,且格点的位置按原预报区域的顺序排列。
本文采用预报区域等面积划分数据分解方式使负载平衡。这时各个结点基本执行相同的任务,只是数据不同。每一个进程的负载是固定的。
2.3 两个主要问题在并行半拉格朗日浅水波模式中,主要解决两个问题:一是有关HALO的问题; 另一个是有关求解赫姆霍兹方程的并行算法的问题。
2.3.1 关于HALO的处理采用半拉格朗日方法的并行计算方法,子区域的周围设有一个环形过渡区域,称为HALO。HALO的宽度可以由初始时刻的最大风速决定,并且一经确定后,在预报过程中保持不变。
在并行半拉格朗日浅水波模式中,按结点个数进行划分后,相邻的结点之间有重叠的区域,在进行中间变量的运算中,仅需有一行 (列) 重叠; 在求出发点变量的运算中,则要考虑风速对于出发点的影响,根据需要确定各结点之间传送的列数; 在解赫姆霍兹方程的运算中,按所用算法,只需有一行 (列) 重叠。Y方向边界的HALO取法为把上下边界值分别等值外推所需行数,当出发点在计算范围以外时,以边界点替代。
将HALO分为八个部分。如果X方向扩充额外的idx列 (左右各idx /2列),Y方向扩充额外的idy行 (上下各idy/2行),且每个结点内部有k 1行,k 2列时,HALO可用数组表示为:左 (idx /2,k 2),右 (idx/2,k 2),下 (k 1,idy/2),上 (k 1,idy /2),右下 (idx /2,idy/2),左下 (idx/2,idy/2),右上 (idx/2,idy/2),左上 (idx/2,idy/2) (如图 2)。每个结点首先判断自己在整个预报区域的位置。如果结点的某一边是外边界,则相应HALO中的格点值由边界值外推给定。如果是内边界,则结点间需要进行信息传递。
但是,采用这种方法确定的HALO中只有约18 %~31 %是实际被用到的,因此我们采用动态HALO,即在时间积分的每步HALO的宽度都可变,且尽量只包括实际被使用的格点,本文对此做了初步的探讨。
由于需要传递的格点资料的多少与风速有关,所以确定传送的格点排数为并行半拉格朗日浅水波模式的难点。如果用初始时刻最大风速决定HALO的宽度,并在以后的积分过程中,保持固定不变,则当某个结点内风速较小时,HALO中只有很少一部分点是有用的,造成了传递HALO时通讯时间的浪费。本文使在每一步时间积分时,每个结点可以根据自己上一时刻HALO及本结点中的最大风速确定此时刻的HALO的宽度。
在开始下一步时间积分时,首先求出本结点 (包括HALO) 中X方向和Y方向风速的最大最小值。根据此最大最小值确定HA LO的宽度。令结点下一时间步长的HALO宽度在左、右、上、下分别为idxl、idxr、idyu、idyd,它们是最大最小风速的函数:
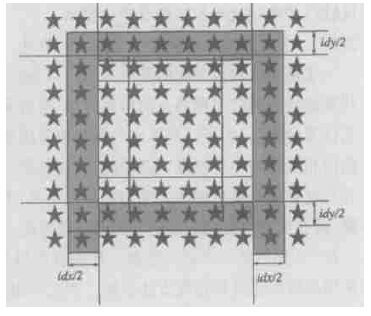
|
|
| 图 2. 格点在结点上的分布示意图和HALO示意图 (在某一个结点上的格点分布) (灰框代表本结点的HALO,是周围结点需要与本结点交换数据的格点。4条长直线所框的点为本结点的内点。本文idx和idy取为2) | |
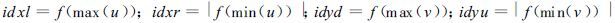
|
仍将HALO分为八个部分。每个结点首先判断自己在整个预报区域的位置。如果结点的某一边是外边界,则相应HALO中的格点值由边界值给定。如果是内边界,则结点间需要进行信息传递。本结点需向相邻结点发送自己所需的HALO的宽度值idxl 、idxr、idyu、idyd,然后相邻结点按所接收到的宽度值发送过来相应的格点值。
这样HALO的宽度在时间积分的每步,每一结点都是不同的。有了一定的针对性和灵活性,能减少一些不必要格点的信息传递。但因为与原方案相比,增加了关于HALO宽度的信息传递,所以抵消了一部分可变HALO带来的好处。由于时间关系,此问题以后做进一步的研究。
在并行差分浅水波模式中,相邻的结点之间仅需有一行 (列) 重叠,所以该模式中HALO的确定比半拉格朗日模式简单。
2.3.2 有关求解赫姆霍兹方程的并行算法求解赫姆霍兹方程的算法中,Gauss-Seidel迭代方法具有很好的收敛性,但采用该迭代法进行计算时与网格点的排序有关,通常采用从左到右,自下而上的顺序,这是一种逐点计算的方法,为了计算某点的函数值需用到刚刚计算完的前面若干点的函数值,具有很强的相关性和串行特点,这种特点使这种方法不适合在并行计算机上使用,本文采用适合并行计算的奇偶排序法。采用这种方法后,不再是只能逐点计算了,而是可以多点同时计算,因为所有奇点 (偶点) 的计算都是独立的,并行度为 (N ×N)/2。对于足够大的N,(N ×N)/2仍然是一个很大的数。把积分区域按结点个数及几何形状分解成若干子区域,采用高效快速并行迭代方法求解。本文采用切比晓夫加速法:
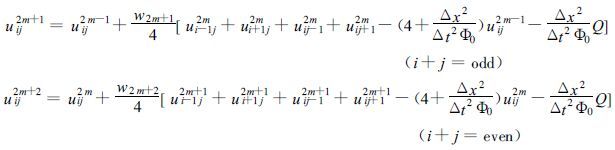
|
其中,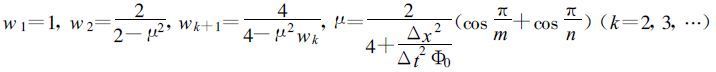
为使结果更具代表性和针对性,本文对模式的时间积分循环部分进行了测试,即运行时间中不包含资料输入输出的部分。计算时间用墙钟时间表示。加速比为:单CPU运行时间除以多CPU运行时间; 并行效率为:加速比除以CPU数量。试验所用的模式:(1) 半拉格朗日浅水波模式Ritchie方案; (2) 欧拉差分浅水波模式Shumann方案。
为验证Ritchie模式的预报效果,我们用Shumann模式作比较,为此设计了试验方案 (1) :两个模式在不同分辨率下作预报效果的比较,由于半拉格朗日方法的特点,前者时间步长约为后者的7到10倍。分别积分5天,可以看出,结果基本吻合 (图略)。说明模式设计正确。
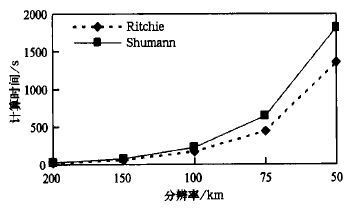
我们知道,模式分辨率的提高会引起计算量的急剧增加,主要表现在两个方面:一是预报区域的格点数成二次方增加; 另一方面,由于格距减小,为了满足计算稳定性条件必须相应地缩短时间步长。为研究水平分辨率的提高对计算量的影响,设计了试验方案 (2) :串行Ri tchie、Shumann模式在不同分辨率下计算时间的比较。预报时间为5天,分辨率分别为200 km,150 km,100km,75 km,50 km。结果如图 3所示。可以看出:当积分区域固定时,随着格距的减小,格点数增加,计算量的差异是明显的。当分辨率增加4倍时,Shumann模式计算量较大; 而对于Ritchie模式,由于时间步长仍取得较大,计算量相对较小。可见采用半拉格朗日方法在高分辨率时可以有效地提高计算速度,节约计算时间。
|
|
| 图 3. RITCHIE和SHUMANN模式在不同分辨率下单结点的计算时间 | |
为研究分辨率的提高对模式并行效率的影响,设计了试验方案 (3),在固定区域,不同分辨率下,用不同数量的结点运行两个模式。比较其计算时间,并行加速比和并行效率。
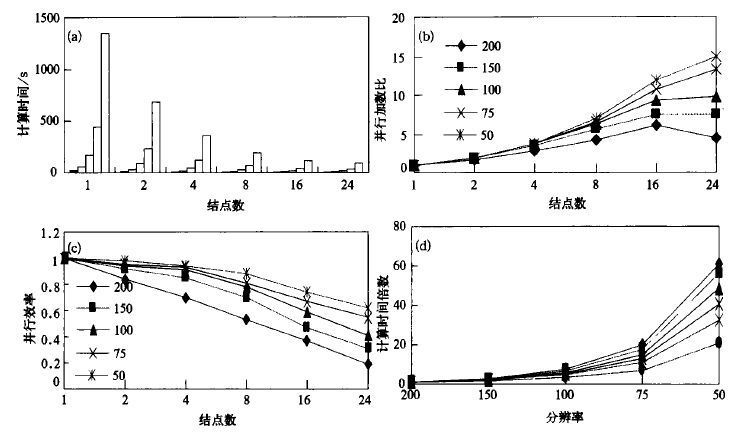
图 4(a) 给出了Ritchie模式在不同分辨率和不同结点数下单结点的计算时间。可以看出:采用并行计算,模式分辨率提高 (格点数增加) 所造成的墙钟时间的延长,要小得多 (如图 4(d))。说明并行模式更适合于计算量大 (如高分辨率、物理过程复杂) 的模式。
|
|
| 图 4. (a) RITCHIE模式在不同分辨率和不同结点数下单结点的计算时间 (每一结点数从左到右分辨率依次为200,150,100,75,50 km); (b) 并行加速比; (c) 并行效率; (d) 不同分辨率不同结点数下计算量倍数的比较 (计算时间的倍数指以分辨率为200 km时的计算时间为1。结点数由上而下为1,2,4,8,16,24) | |
图 4(b) 给出了Ritchie模式在不同分辨率下的并行加速比。可以看出,在结点数相同的情况下,分辨率越高,并行加速比越大。当分辨率低时,随着结点数的增加,并行加速比的增加幅度较小。如分辨率为50 km时,结点数由2个增加16个,其中到16个结点时,并行加速比增加的幅度仍较大。说明当计算量一定时,运算并行模式所需的结点并不是越多越好。这是因为结点增加,通讯量也相应增加,抵消了一部分计算速度加快所省的时间。应根据所解问题计算量的大小,确定使用合理的结点数,以求达到在较高的并行效率下,既提高计算效率,又不浪费计算机资源的目的。另一方面,每个结点的内点量与所需通讯量之比越大,即结点计算量相对于通讯量越大时,并行计算的优势越明显。
图 4(c) 给出了Ritchie模式在不同分辨率下的并行效率。可以看出:虽然随着结点数的增加,并行效率是减小的,但当分辨率较大时,并行效率减小的幅度较小。即格距小,格点数量大时,增加结点能获得较好的并行效率。在分辨率为50 km时,格点数量很大,并行效率很高,甚至接近1。这说明模式分辨率越高,格点数量越大引起的计算量越大时,并行计算的效果越好。
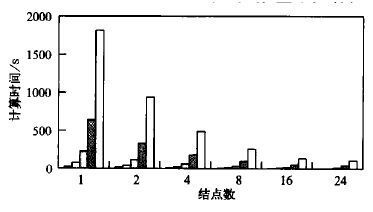
试验方案 (3) Shumann的结果如图 5所示。可以看出,与半拉格朗日模式相比,随着分辨率的提高,Shumann模式计算量增长的幅度比较大。并行加速比和并行效率较高,这主要是由于半拉格朗日模式比Shumann模式需要传递的格点数多。
|
|
| 图 5. SHUMANN模式结果 (说明同图 4a) | |
综合上述情况,可以看到,使用半拉格朗日方法处理平流项是有利的,在模式分辨率高,计算量大时,可有效地提高计算速度。
4 结论本文针对使用半拉格朗日方法处理平流的浅水波模式的并行化问题,主要做了两方面的工作:首先建立了Ritchie方案处理平流的浅水波模式,然后在SP2机MPI环境下实现了并行方案并试验。得出以下结论:
(1) 在模式分辨率高,计算量大时,使用半拉格朗日方法处理平流项是有利的,可有效地提高计算速度。
(2) 采用分区域并行计算的方法,半拉格朗日方法并行效率较好。
(3) 模式并行以后,在固定区域,对于某一分辨率的模式,随着结点数的增加,模式计算速度提高,并行加速比增大,并行效率降低; 对于不同分辨率的模式,分辨率高的,随着结点数的增加,并行加速比较大,并行效率较高。说明在模式分辨率高时使用并行半拉格朗日模式是必要的,可行的。
致谢 在完成上述工作过程中得到了刘金达等同志的帮助和指导,在此表示感谢!| [1] | Ritchie H, Implimentation of the semi-Lagrangian method in a high-resolution version of the ECMWF forecast model. Mon Wea Rev, 1995, 123: 489–514. DOI:10.1175/1520-0493(1995)123<0489:IOTSLM>2.0.CO;2 |
| [2] | Staniforth A, Cote J, Semi-Lagrangian integration schemes for atmospheric models--A review. Mon Wea Rev, 1991, 119, (9): 2206–2223. DOI:10.1175/1520-0493(1991)119<2206:SLISFA>2.0.CO;2 |
| [3] | Temperton C, Staniforth A, An efficient two-time-level semi-Lagrangian semi-implicit integration scheme. Quart J Roy Meteor Soc, 1987, 113: 1025–1039. DOI:10.1002/qj.49711347714 |
| [4] | Chen Jiabin, Wang Jun, Studies on non-interpolating semi-Lagrangian schame and numerical solution to KDV equetion. Adv in Atmos Sci, 1996, 13, (2): 265–271. DOI:10.1007/BF02656869 |
| [5] | 董敏. 半拉格朗日方法及其在数值模拟和数值预报中的应用. 应用气象学报, 1997, 8, (1): 99–107. |
| [6] | 廖洞贤,张玉玲. 原始方程模式的分解算法和半拉格朗日方法. 廖洞贤, 柳崇健主编. 数值天气预报中的若干新技术. 北京:气象出版社, 1995. |
| [7] | 陈景良. 并行数值方法. 北京:清华大学出版社, 1983. |
| [8] | 孙家昶, 张林波, 迟学斌, 等. 网络并行计算与分布式编程环境. 北京:科学出版社, 1996. |
| [9] | 冯康. 数值计算方法. 北京:国防工业出版社, 1978. |
| [10] | 颜宏. 大规模并行计算-21世纪气象数值模拟与预报的未来. 廖洞贤, 柳崇健主编. 数值天气预报中的若干新技术. 北京: 气象出版社, 1995. |
| [11] | 刘金达. 并行浅水波谱模式的初步试验. 国家气象中心科技年报, 1995, (A册). |
| [12] | 金之雁, 颜宏, 丁小良. 数值天气预报并行计算模式的设计与可行性讨论. 应用气象学报, 1993, 4, (1): 117–121. |
| [13] | 金之雁, 颜宏. 有限区域模式并行计算试验. 高原气象, 1996, 15, (1): 62–68. |
| [14] | 喻炜, 颜宏, 金之雁. 并行效率的初步研究. 应用气象学报, 1996, 7, (1): 61–68. |
| [15] | Ritchie H, Eliminating the interpolation associated with the semi-Lagrangian scheme. Mon Wea Rev, 1986, 114, (1): 135–146. DOI:10.1175/1520-0493(1986)114<0135:ETIAWT>2.0.CO;2 |
| [16] | Grammeltvedt A, A survey of finite-difference schemes for the primitive equations for a barotropic fluid. Mon Wea Rev, 1969, 97, (5): 384–404. DOI:10.1175/1520-0493(1969)097<0384:ASOFSF>2.3.CO;2 |
 2004, 15 (4): 417-426
2004, 15 (4): 417-426

