干旱是水分持续亏缺的一种异常气象现象,是主要自然灾害之一。我国干旱发生频繁,旱情严重。随着全球变化,气候变暖,将有可能产生更为严重的干旱。为了评估干旱程度就迫切需要建立一个衡量干旱严重程度的标准,即干旱指标。国内外学者提出了各种形式的指标,其中W.C.帕默尔提出了“对当前情况气候上适应的降水”即CAFEC(Climatical Appropriate for Existing Condition)降水的概念,从而推导出一套分析计算干旱严重程度的完整方法。帕默尔旱度模式具有严密的系统性,考虑因子较全面,综合了水分亏缺量和持续时间因子对干旱程度的影响,并考虑到前期天气条件,对于干旱的各项特征能较合理地进行描述,且具有较好的时空比较性。帕默尔干旱指标在美国广泛应用,是美国海洋大气局发布的天气-作物周报中的主要内容[1]。1984年范嘉泉等人介绍了帕默尔气象干旱指标的原理、优点及计算方法[2]。根据其思路,1985年安顺清等人用济南和郑州等站的资料对帕默尔旱度模式进行了修正,建立了我国的气象旱度模式[3~4]。但这个修正的帕默尔旱度模式中也存在着一些问题,针对这些问题我们对帕默尔旱度模式进行了进一步的修正,以使其更客观地评价干旱的发生及程度。
1 帕默尔旱度模式的修正 1.1 修正方案根据帕默尔旱度模式的原理和思路,1985年安顺清等人用济南和郑州等站的资料对帕默尔旱度模式进行了修正,建立了我国的气象旱度模式并进行了初步应用。但其中也存在着一些问题:
(1) 帕默尔旱度模式及我国修正的帕默尔旱度模式在建模和修正权重因子K时所选用的站点较少,前者建模选用了2个站点,修正权重因子K时又选用了7个站点; 后者建模时选用了2个站点,修正时又选用了12个站点,要想正确评估全国干旱应选取更多的具有代表性的站点。
(2) 帕默尔旱度模式是以水分平衡为基础的,可能蒸散是采用桑斯威特方法计算的,这种方法是在美国建立的,考虑因素只有温度,且假设当温度低于零度时没有蒸散,因此在我国应用有较大偏差,应采用更精确的方法。
(3) 安顺清等在修正帕默尔旱度模式时做了这样的假设: 上层土壤田间有效持水量为25 mm,下层土壤田间有效持水量分为两种,其中西安、汉中、沈阳、汉口、昆明和梧州取175 mm,其余各站取125 mm,这样的划分过于粗糙,且数值偏小,因此不同区域的土壤田间有效持水量划分应更细一些,其数值应根据我国土壤田间有效持水量资料确定。
(4) 我国修正的帕默尔旱度模式是1985年建立的,应用这个模式分析了1951~198年的干旱程度及发生规律,但1980年以来干旱很严重,需要进一步修正模式以使之适合评估近年来的干旱。
针对以上问题,我们通过以下改进来进一步修正帕默尔旱度模式:
(1) 在建立旱度模式和修正权重因子的过程中选用较多的站点。在建模过程中选择了济南、郑州和太原3个站,在修正权重因子的过程中选择了哈尔滨、佳木斯、呼和浩特、沈阳、北京、固原、西安、汉中、青岛、德州、运城、长沙、武汉、南昌、杭州、福州、广州、昆明、南宁、成都和贵阳21个站。站点资料年限由1961年到2000年。
(2) 对可能蒸散量的计算采用彭曼-蒙蒂斯修正公式[5]:
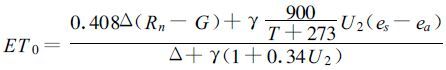
|
(1) |
式中ET0 为可能蒸散量(mm°d-1) ,Rn 为地表净辐射(MJ°-2°-1) ,G 为土壤热通量(MJ°-2°-1) ,T 为平均气温(℃),U2为2 m高度处的风速(m°s-1) ,es 为饱和水汽压(kPa),ea 为实际水汽压(kPa),Δ 为饱和水汽压曲线斜率(kPa°℃-1) ,γ为干湿表常数(kPa°℃-1) 。
这种方法是FAO提出的计算可能蒸散量的首选方法,它不需要进行地区修订,也不需要改变任何参数便可适用于中国和世界各个地区,其计算结果与实际测量的可能蒸散量更为接近,适用于帕默尔旱度模式以月为单位的可能蒸散量的计算[6]。
(3) 根据《中国土壤图》、《中国土壤分区图》及各个站点的实际情况,对于没有测定土壤田间有效持水量的站点进行较准确的估计。将土壤分为上下两层,上层(0~20 cm)土壤田间有效持水量取40 mm,下层(20~100 cm)土壤田间有效持水量分三种情况,一是佳木斯、呼和浩特、哈尔滨、太原、西安取150 mm,二是固原、运城、沈阳、北京、济南、郑州、德州和汉中站取200 mm,其余各站取250 mm。
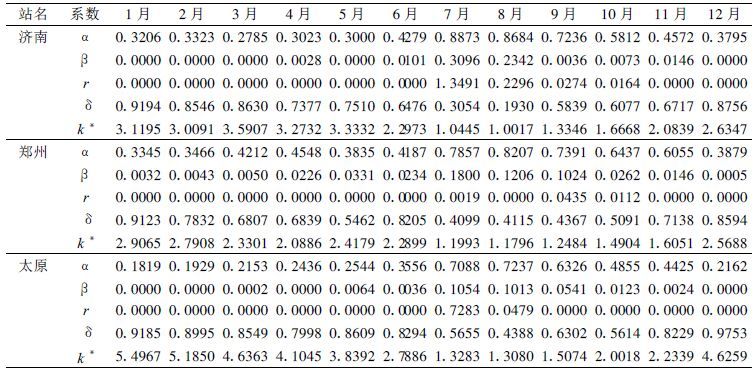
1.2 修正的帕默尔旱度模式的建立首先根据帕默尔水分平衡各分量计算方法[1]建立济南、郑州和太原的水文帐并求出水分平衡各分量的平均值、各气候常数(表 1) 和各气候适宜值。
|
|
表 1 济南、郑州、太原的气候常数 |
各气候常数为水分平衡各分量的平均值与平均可能值之比,计算公式如下:
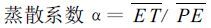
|
(2) |
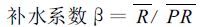
|
(3) |
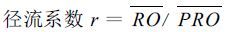
|
(4) |
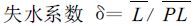
|
(5) |
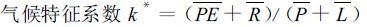
|
(6) |
其中E T为月平均实际蒸散量,PE 为月平均可能蒸散量,R 为月平均补水量,PR 为月平均可能补水量,RO为月平均径流量,PRO为月平均可能径流量,L 为月平均失水量,PL为月平均可能失水量,P 为月平均降雨量。PE+R 表示月平均水分需要,P+L 表示月平均水分供给,两者的比值能够反映出不同地区和时期的水分气候差异,它是气候特征值的一级近似。
由表 1 计算出的各气候常数可计算出水分平衡各分量的气候适宜值:
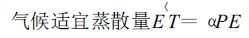
|
(7) |
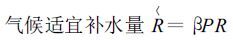
|
(8) |

|
(9) |
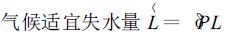
|
(10) |
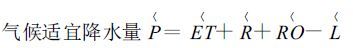
|
(11) |
其中PE 为月可能蒸散量,PR 为月可能补水量,PRO 为月可能径流量,PL 为月可能失水量,其他符号与前相同。
实际降水量与气候适宜降水量的差值称为水分距平值d:
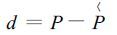
|
(12) |
其中P为月降水量。
由此可以求出各月水分距平指数z值(即未经修正的Z):
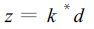
|
(13) |
z 值不但可以表示干旱,而且也可以表示湿润; 在干期z值为负,表示气候为负异常,在湿期中,z 值为正,表示气候为正异常。
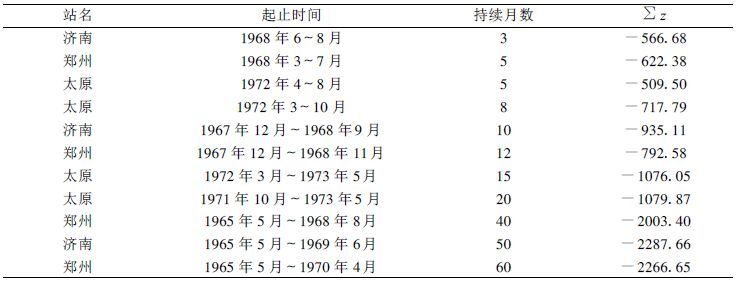
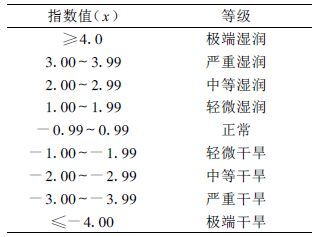
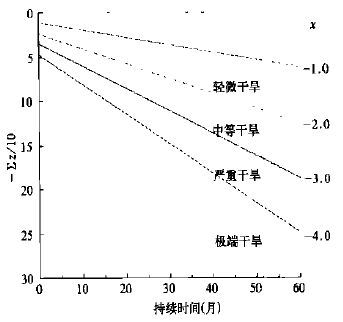
在计算各站气候常数和气候适宜降水量的基础上,根据干旱严重程度是持续时间和水分亏缺量的函数的原理,建立旱度模式。表 2 给出了选取济南、郑州和太原3个站历史资料中不同持续期最旱时段和对应的累积z值(表 2) ,并假定这些最旱时段为极端干旱作图,令x=-4.0,将纵坐标从正常到极端分成四等份,作出另外三条直线,分别表示严重、中等和轻微干旱,x 值分别等于-3.0、-2.0和-1.0(图 1) 。干湿等级的规定仍旧采用帕默尔旱度模式的划分标准,如表 3。
|
|
表 2 济南、郑州和太原3个站最旱时段的Σz 值 |
|
|
| 图 1. 干旱等级与水分距平指数累积量和持续时间的关系 | |
|
|
表 3 帕默尔指数干湿等级 |
根据图 1,并假定历史资料中最旱时段为极端干旱,x ≤-4.0,则可建立某月干旱指数值的模式:
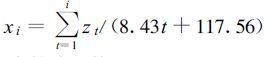
|
(14) |
式中t为持续月数。
式(14) 并不能立即应用,因为干旱期起始时的累积值不同,甚至会出现这样的情况,即某两个月的z值虽相同,但一个出现在几个较湿润月之后,另一个出现在几个较干旱月之后,则两者的干旱指数会不同。因此必须确定每个月的z值对干旱指数xi的影响。
令i=1,t=1,则
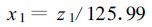
|
(15) |
设这个月是干旱期的开始,则
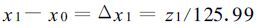
|
(16) |
如果要维持上个月的旱情,随着时间t的增加,-Σz 必须增加。但t的增加是恒定的,即每月增加1,因此,维持上个月的旱度值所需要增加的z值取决于x值,故令
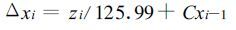
|
(17) |
当t=2,xi-1=xi=-1时,则C=-0.0669。将其代入式(17) 得:
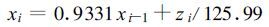
|
(18) |
此式即是计算干旱指数的基本模式。
式(18) 是根据济南、郑州和太原3个站的资料建立起来的,用于其他地区肯定不适合。要解决这个问题,使式(18) 计算出的干旱指数有较好的空间比较性,就要对权重因子进行修正。假设一年中每个月x=-4.0,则t=12代入式(14) 得
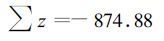
|
(19) |
因假设这12个月对于任何地区都表示极端干旱,所以当用-874.88除以某地12个最干旱月的水分距平总和Σd(代表该地极端干旱)时,就得到了当地12个月期间的极端干旱平均权重因子K。
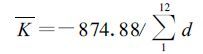
|
(20) |
如前所述,气候特征k*的估计值K取决于平均水分需要和平均水分供给的比值,在平均水分需要中除平均可能蒸散量PE 和平均补水量R外,还应包括平均径流量RO,此外k*值显然还与D(d 的绝对值平均)成反相关。根据前述21个站的结果作出回归方程如下:
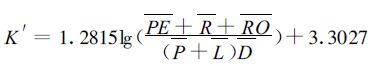
|
(21) |
如果K′值从空间比较性的角度来说是完全合理的话,则每个站的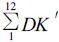
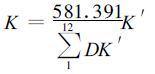
|
(22) |
经过最后权重的z值写成Z,且Z=Kd,这就是最后所用的水分距平指数值。
应当指出,对应于Z值,应用式(18) 计算干旱指数时,还必须确定干旱开始与结束。我们将x=-0.5作为干旱与正常的临界值,当xi >-0.5时干旱就结束。那么在一个月内使x达到-0.5需要多少水分(Z)值? 根据式(18) 得到:
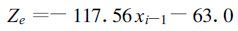
|
(23) |
若令,Δxi=0,xi-1=-0.5,则Z=-4.21,这表明若某个月达到干旱标准,其后的月份即使天气比正常略干,干旱也趋于结束。
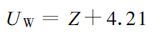
|
(24) |
把UW 定义为“有效增湿量”。
如果第一个是湿润月结束一次干旱所要求的Z值大于U,那么旱情将减轻,但旱情不一定会结束,则下个月结束这次干旱所需Z值将减小,故结束一次干旱所需总Z值为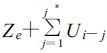
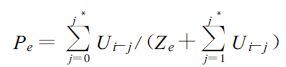
|
(25) |
只要将上述结果稍加改动,即可用于湿润期。如将x=+0.5代入式(18) ,得
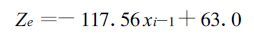
|
(26) |
则“有效增干量”为
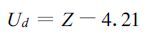
|
(27) |
湿润期结束的概率仍用式(25) 表示。
根据干期和湿期开始及结束的概率最后决定各月的干旱指数值x。
2 修正的帕默尔旱度模式计算结果及其验证我们利用新建立起来的旱度模式计算了我国139个站点的逐年逐月干旱指数值。下面将北京、西安和贵阳有关文献描述的实际旱情[6~8]和计算的旱度值相对照,以验证模式的合理性。
2.1 北京实际旱情与计算的帕默尔指数值对照干旱灾情: 1965年北京5~10月总降水量比常年同期少四成,旱情严重; 1968年上半年降水量是1889年有气象记录以来同期的最少值,农业生产受到严重影响; 1972年北京市严重干旱,小河溪提前断流,5月中下旬大多中小型水库的水都已放空,9月1日密云水库仅蓄水6.388 m3,比蓄水很少的1971年同期还少2.278 m3,官厅水库仅蓄水1.78×108 m3,是历年同期蓄水最少的一年,地下水位大幅度下降,一般下降3~5 m,造成1.4万眼机井有一半抽不上水来,3.5×104 hm2 秋收作物到7月19日才种上; 1980~1984年连续少雨,干旱严重时密云水库停止沿途的农业用水,地下水开采量大于补给量,地下水位平均下降4.43 m,其中1980年北京7月上旬到8月上旬降水量是近百年来同期的最小值,郊区80多座大、中、小型水库和400多座塘坝、截流工程陆续干涸或降到死水位以下,全市大、中、小河道基本断流,地下水位比1979年同期下降3~5 m,全市3. 万眼机井有近6000眼干涸,使郊区210多个村庄7万多人吃水发生困难,粮油作物普遍受旱,有13.4×104 hm2 严重减产,有3.4×104 hm2 绝收或基本绝收,春季育的树苗大面积枯死; 1983年因旱有350家工业企业限制用水,不少工厂停工停产; 1989年1~9月全市平均降水量比上年同期少二成,10月初,官厅水库蓄水接近死库容,到8月底,全市地下水平均埋深比上年同期下降2.03 m ; 1993年是北京1905年有降水记录以来的第四个少雨年,使北京市陷入水危机中; 1994年春旱严重,夏粮都减产。
湿涝灾情: 1963年8月降雨量比多年平均多近3倍,仅8日、9日两天就达337 mm,发生短时洪涝,交通受到影响; 1969年7、8月降雨量比常年同期多近八成,涝害较重; 1977年6月降水量比常年同期多近一倍,连阴雨天气影响小麦脱粒、晾晒及夏播; 1978年秋季出现连续阴雨天气,影响粮食作物及蔬菜等生长; 1979年6、7月出现短时洪涝; 199年7月多条河流发生洪水,十三陵水库水位上升到1974年以来的最高值,延庆、昌平等县出现了桥梁被冲断以及滑坡、塌方的现象,农田受淹、庄稼倒伏、牲畜被冲走、民房倒塌和供电设备冲毁。
以上实际旱涝灾情记录与计算的帕默尔指数值(图 2) 对照是基本符合的。
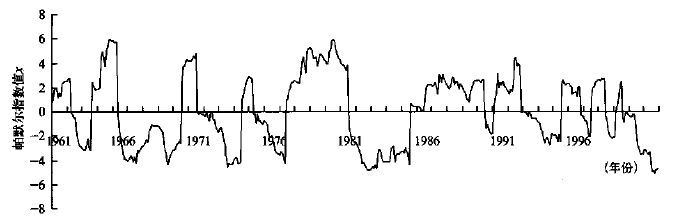
|
|
| 图 2. 北京1961~2000年逐月x值 | |
2.2 西安实际旱情与计算的帕默尔指数值对照
干旱灾情: 1962年3~5月总雨量是40年来最小值,春播困难,作物缺苗现象严重,有的干死; 1966年底墒不足,再加上春季降水又少,对春播造成影响; 1967年夏季降水比常年同期少三成,出现夏旱; 1969年5~8月总雨量是40年来同期的最小值,不少河流断流,秋作物遭到严重危害,有些地方人畜饮水困难; 1971年7~9月总雨量比常年同期偏少四成,大秋作物生长受到影响; 1978年3月降水稀少,影响越冬作物的生长,春播困难,冬小麦受旱严重甚至死苗,4月有的地方麦田土壤湿度降至10%以下,干土层达34 cm,有的被旱死; 1986年7、8月久晴少雨,秋作物受旱面积占播种面积的一半; 1994年5月气温高降水少,小麦青干逼熟,夏粮减产两成; 1995年年降水量为40年来最小值,遭受百年一遇特大干旱,受旱面积占播种面积的70%,粮食大面积减产甚至绝收,人畜饮水困难,中小河流大部干涸,地下水位大幅度下降,城市供水仅及正常供水量的一半。
湿涝灾情: 1965年7月降水比常年同期多近五成,出现涝灾; 1976年8月降水比常年同期多一倍,出现洪涝灾害; 1981年7、8月降水比常年同期多一倍,河水暴涨,农田被淹,路桥被冲毁; 1988年7、8月降水比常年同期多近八成,渍涝灾害严重,粮食减产; 1998年7、8月连降暴雨,降水比常年同期多八成,洪涝灾害严重。
以上旱涝灾情与计算的帕默尔指数(图 3) 对照是较为一致的。
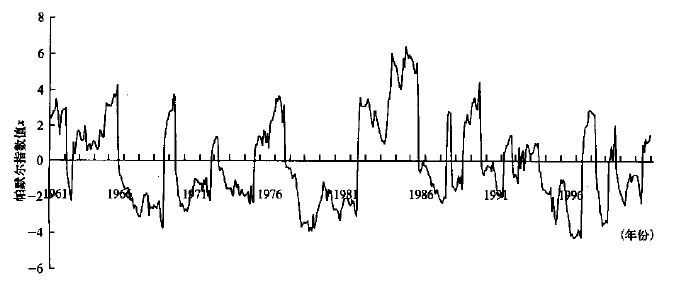
|
|
| 图 3. 西安1961~2000年逐月x值 | |
2.3 贵阳实际旱情与计算的帕默尔指数值对照
干旱灾情: 1962年冬季和1963年春季少雨,冬春连旱,小春作物生长、发育及早稻播种育秧、栽插受到影响,产量减少; 1966年冬春连旱,小春作物有的干枯死亡,大春作物春播、栽插推迟; 1970年冬春持续少雨,不少河流断流,塘堰无水,小春作物减产; 1972年~8月降水偏少,干旱持续二三个月; 1978年7~9月降水少,中稻、双季晚稻、棉花等作物因旱大量死苗,地下水位下降,塘、堰、库、河干涸,人畜饮水困难; 1990年从7月初开始少雨,尤其是8月中旬到9月中旬雨量之少为40年同期所未有的,各种作物受旱面积都在五成以上,池塘、水井干涸,人畜饮水困难,乌江渡水库的来水量比往年同期减少一半,使贵阳电厂不能发电或少发电,一些城镇实行限电措施。
湿涝灾害: 1977年6月连降暴雨或大暴雨,发生洪涝灾害; 1991年5~8月连降暴雨,特别是7~8月降水比常年同期多一倍以上,洪涝灾害严重,农田淹没、房屋倒塌、经济损失巨大。
以上旱涝灾情记录与计算的帕默尔指数值(图 4) 对照是基本一致的。
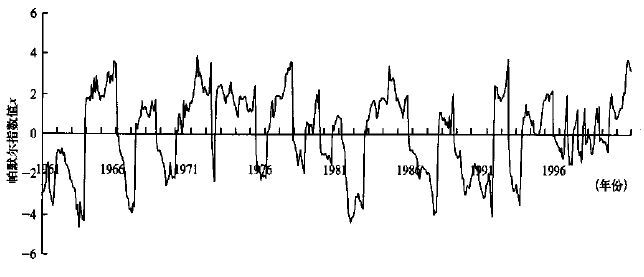
|
|
| 图 4. 贵阳1961~2000年逐月x值 | |
其他站点实际旱涝灾情与计算的帕默尔指数值的对比验证也十分吻合,在此不再赘述。由此可见进一步修正的旱度模式所计算的结果能够较好地表示出旱涝程度,特别是对一些严重干旱期更是如此。
3 小结与讨论综上所述,进一步修正的帕默尔旱度模式提高了原有模式的科学性。通过对北京、西安和贵阳等站的实际旱涝灾情的对比验证表明帕默尔旱度模式能较客观地反映实际旱涝灾情,特别是对一些严重的干旱时段更加吻合。因此,新修正的帕默尔旱度模式适合评估我国大部分地区的干旱情况。本旱度模式是建立在单个站点基础上的,如果想要评估区域性的干旱则应该以区域的气候资料为基础重新修正模式,这样才能客观地反映区域性的干旱程度。同时还应指出该模式是用来评估气象干旱的,对于农业干旱来说,其实际干旱严重程度还与农作物状况和人为活动有关,如2002年虽然北京地区已连续第四年干旱,但由于农作物需水关键期下了雨,实际旱情要轻于帕默尔指数值所反映的旱情。另外,由于人为活动有时导致旱情加剧,如上游层层拦截导致下游水资源枯竭,超采地下水导致水位下降,甚至影响土壤含水量,有时导致旱情减轻,如灌溉等,这些在该模式给出的气象干旱指数上并不能反映出来,如要准确评估农业干旱还应考虑农作物需水规律和人为活动的影响(如灌溉等)。
| [1] | Palmer W C, Meteorological Drought. Research Paper, No45, 1965. |
| [2] | 范嘉泉, 郑剑飞. 帕默尔气象干旱研究方法介绍. 气象科技, 1984, 12, (1): 63–71. |
| [3] | 安顺清, 邢久星. 修正的帕默尔干旱指数及其应用. 气象, 1985, 11, (12): 17–19. |
| [4] | 安顺清, 邢久星. 帕默尔旱度模式的修正. 气象科学研究院院刊, 1986, 1, (1): 75–81. |
| [5] | 刘钰, PereiraL S, TeixeiraJ L. 参照蒸发量的新定义及计算方法对比. 水利学报, 1997, (6): 27–33. |
| [6] | 中国重大自然灾害及减灾对策(分论), 北京: 科学出版社, 1993. |
| [7] | 中国主要气象灾害分析(1951-1980年), 北京: 气象出版社, 1985. |
| [8] | 中华人民共和国国家统计局、中华人民共和国民政部. 中国灾情报告1949~1995. 北京:中国统计出版社,1995. |
 2004, 15 (2): 207-216
2004, 15 (2): 207-216