2. 中国气象局, 北京 100081;
3. 国家气象中心, 北京100081
2. China Meteorological Administration , Beijing 100081;
3. National Meteorological Center , Beijing100081
嵌套模式中侧边界的处理是关系模拟成败的重要因素[1, 2],侧边界所带来的误差是有限区域预报模式的主要误差来源之一。在天气尺度预报中侧边界嵌套误差主要有三个方面的来源,一是由于差分方程代替微分方程及侧边界的超定义导致计算波的产生并在边界附近发生反射、折射等; 二是天气尺度的波动在移入细网格时,由于格距的不同,模式大气中天气尺度波动的相速差等造成预报的“失真” ; 三是非绝热过程中由于粗细网格对参数化方法模拟的次网格尺度强迫项的不同造成虚假的非绝热平流[3]。这几个主要原因造成侧边界附近的预报误差,甚至发生计算不稳定。有限区域气候模式关心的是大气运动平均状况的模拟,因此对气候模拟影响更大的是上述误差的积累情况,以及这些误差之间的相互非线性作用对气候模拟的影响严重程度。目前一些区域气候模式为了解决侧边界误差把侧边界过渡区取得很宽,在东西方向仅85个格点的区间中侧边界区由天气尺度中的4~6圈增到18圈,这说明在气候模式中侧边界误差对内区的影响更为严重; 尤其当垂直分辨率加大时,侧边界区水平圈数也将加大; 从这个意义上来说,侧边界问题在有限区域气候模拟中更为重要。
目前用嵌套气候模式模拟区域气候特征的工作已有很多[4, 5, 6],而对侧边界处理造成的误差随时间的积累性,这种误差与其它误差来源之间的非线性作用的问题的研究远远不够。因此,有必要对区域气候模拟中边界嵌套误差的种类、来源及时空演变特征做一比较系统的研究分析,同时这也是进一步设法减小误差所必须的基础工作。本文将通过一系列的诊断试验,从分析这些误差来源着手,对这些误差来源尽可能予以分离并分别进行诊断,研究各种误差的相对重要性、时空分布特征以及对气候模拟影响的严重程度,从而为改进侧边界方案提供依据。
1 模式简介和方案设计本文以颜宏[7, 8]设计的“复杂地形条件下嵌套细网格模式”(下称YH模式)为基础,YH模式在设计上具有较高的灵活性,用户可以通过参数的设定选取不同的数值方案与物理过程参数化方案,从而便于侧边界误差的研究要求。
在误差诊断时,首先需要确定一个参考场。在过去工作中参考场一般选取实况场或各种分析场等,但由于参考场本身带有的误差,加上观测误差和除侧边界外模式本身的误差等,这些误差和嵌套误差混合在一起,从而无法从中分析嵌套误差分布特征及其产生的原因。为了研究侧边界嵌套误差,我们需要分离出侧边界误差的来源,并以此为依据寻找减少侧边界误差的方法。为能达到此目的,我们设计了一个环圈数值模式系统作为参考场,即将区域的YH模式范围扩充,使其纬向方向为环形,而其经向方向扩展几圈,得到YH模式的环圈模式。环圈模式的初始资料及南北边界资料由T63场库中读出,侧边界输入间隔为24 h,而区域YH模式的初始资料及侧边界资料由环圈YH模式的结果提供,侧边界输入间隔可随需要而定,这时环圈YH模式及区域YH模式所采用的物理过程完全一致,由于侧边界误差主要出现在流入流出量最大的东西侧边界,因此我们可以把环圈YH模式作为无侧边界影响的参考场。
环圈模式预报作为参考场的优点在于:
(1) 大小模式的物理过程、差分格式均相同,因此可以通过参数选择来控制参考场的模式物理过程和分辨率,分离不同物理条件下侧边界的影响。
(2) 此数值试验系统不仅可以用以对侧边界误差进行诊断分析,也可以用来检验新方法的优缺点。我们通过此次误差诊断得出误差分布特点后,通过一定的方法(如采用三维嵌套),尽量减少侧边界误差。同样采用环圈模式作为参考场,诊断新方法下的误差分布特点,就可知道新方法的优缺点。
环圈YH模式的选取范围11.25°S~58.125°N,0°~363.75°E,网格距为1.875°。
有限区YH模式范围为16.875°S~52.5°N,61.875°W~127.5°E,网格距可变,资料选取的时间范围为1997年10月24日~12月4日。
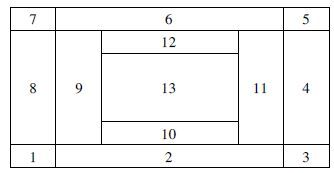
为了能对误差的空间分布作一细致的诊断分析,我们将有限区YH模式的预报区在水平方向上分为13个区,具体分法见图 1。
|
|
| 图 1. 模式分区图例 | |
其中最外几圈即第1区到第8区为模式的外区,圈数的多少取决于模式的边界张弛区,YH模式的边界张弛区为4圈,于是我们取预报区的外面4圈为边界区,其余内部为内区,而边界区内又分流入区和流出区,纬向风流进的地方即西面边界区为流入区,纬向方向风流出的地方即东面边界区为流出区。为尽可能地排除经向风速带来的误差,我们只选取第8区为流入区,选取第4区为流出区。
为简单方便,在垂直方向上只分上、下两层。上、下层的区分根据YH模式的p-σ坐标的分界来取,YH模式在400 hPa以上为p坐标,400 hPa以下为σ坐标,所以取40 hPa以上为上层大气,取400 hPa以下为下层大气,这样给动能的计算带来了方便。
由于嵌套误差的来源是多方面的,各种误差相互作用的过程可能是复杂的。为了分析各种误差的来源,进而找出减少甚至消除嵌套误差及误差积累的办法,在数值试验方案的设计上应遵循如下原则,即分析某种误差来源时应尽量避免其它误差的出现和误差间的相互作用。具体诊断试验方案见表 1。
|
|
表 1 诊断方案的设计 |
为使各物理量在各层之间都有比较性,我们所诊断出的量都除以对应区域环圈Y模式零时刻的原量,即得到各量的变化率,然后对这些变化率做比较分析,以下各图的纵坐标是各种物理量的变化率。
短期气候中误差诊断分析的侧重点和短期天气不同,短期气候侧重于误差的平均积累状况,因此为能分析误差的短期、中期及长期积累性随时间的演变特征,我们对误差分别做了逐日误差绝对值图、误差绝对值5天滑动平均图、误差的5天滑动平均图、误差的10天滑动平均图和30天滑动平均图,以便可以观察误差的变化以及误差的积累特征。
2 数值试验由于嵌套误差有各种来源,如相速误差、地形影响以及物理过程处理不同造成的误差等等,下面我们就各种误差来源进行分析讨论。检验的要素包括动能、温度和降水。
2.1 侧边界嵌套引起的误差特征分析首先为了能对单纯因侧边界嵌套引起的误差场误差特征有一个最基本的掌握,我们设计了试验1方案。试验1选取了无地形、有日变化、非绝热区域YH模式(模式1A),其背景场和参考场都由同等条件下的环圈YH模式(模式1B)提供。大小模式相同的网格距可排除相速误差,模式无地形排除了复杂地形所带来的误差影响,这样区域YH模式的误差纯粹是由于模式侧边界嵌套处理所造成的。
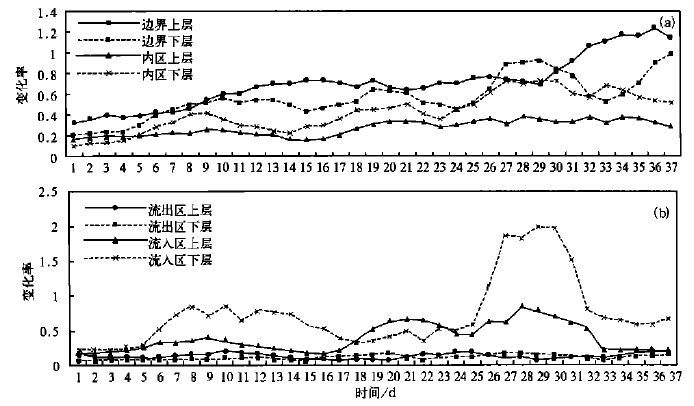
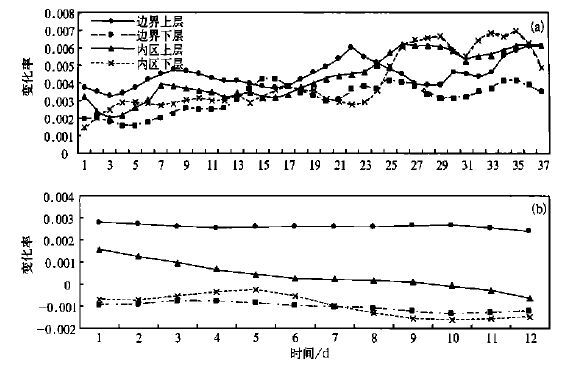
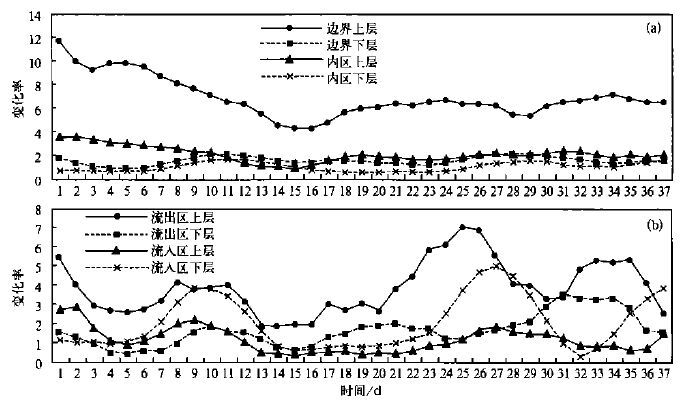
图 2 给出了动能误差的时空分布特征。可以看出,动能的误差比较严重,最大时为原量的一倍以上(图 1) 。无论是短期积分还是长期积分,边界误差大于内区误差,其中边界内,上层误差大于下层误差; 在内区,下层误差大于上层误差; 在边界内,流入区误差远大于流出区误差; 且随着积分时间的延长,这种误差分布更为明显,所以说动能场重要的误差来源于边界上层的流入区误差,且动能场的误差有较强的积累性。对于感热场(图 3) ,从数值上来看,误差的比率较小,为千分之几到千分之十之间。感热场上层误差大于下层误差(3a); 在下层,从开始至20天左右边界误差一直大于内区,20多天以后,内区下层误差大于边界下层误差,因此总体来讲,误差最大区为边界上层; 而从30天平均图上看(3b),边界上层的平均积累性较强,而内区上、下层的积累性很弱,且边界上层和边界下层的数值相反,所以积累性也不是很强,但有一些积累性。总的来看长期时间积分中,边界误差仍是大于内区误差,误差在上层大于下层。从水汽场误差分布特征(图 4) 来看,边界上层的误差最大,远大于内区上层,边界下层误差大于内区下层误差,所以边界区误差明显大于内区误差,上层误差大于下层误差; 在边界,流出区上层远大于其余区的误差,这种分布随积分时间的延长仍很明显,可见水汽误差比较严重,且水汽误差的积累性较强。
|
|
| 图 2. 侧边界输入间隔6 h无地形有日变化非绝热模式动能误差绝对值5天滑动平均分布特征 (a)预报区域,(b)边界区域 | |
|
|
| 图 3. 侧边界输入间隔6 h无地形有日变化非绝热模式温度误差分布 (a)误差绝对值5天滑动平均,(b)30天滑动平均(图例同(a)) | |
|
|
| 图 4. 侧边界输入间隔6 h无地形有日变化非绝热模式水汽误差绝对值5天滑动平均分布特征 (a)预报区域,(b)边界区域 | |
2.2 侧边界输入时间间隔对误差的影响
侧边界输入间隔就是大模式连续两次向小模式提供侧边界资料的时间差,当有日变化的非绝热加热引入模式时,作为侧边界的大范围粗网格预报场,由于模式物理量的差异以及输入资料的时间间隔的限制,有可能产生在预报内区与侧边界区的感热水平差异。这种虚假的感热对比在模式大气表现的比较明显,由此会造成侧边界附近虚假的感热平流。为此采用试验2方案对不同的侧边界输入时间间隔的误差做一比较。
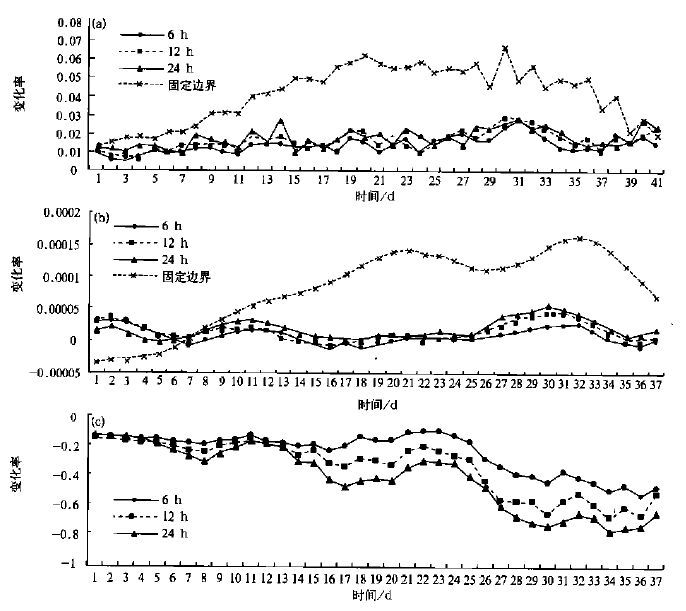
首先,所有的物理量误差当侧边界为固定边界时最大(图 5a、5b)。不同的时间间隔对于感热场来看(图 5a),逐日误差绝对值为24 h误差>12 h误差>6 h误差,但误差积累不是很明显; 太阳辐射误差(图 5b),依次为24 h输入误差最大,其次为12 h误差,最小为6 h输入误差,但长期积分的误差积累仍不是很明显; 而对于动能场误差来说(图 5c),无论是在短期时间积分中还是在长期时间积分中,动能场的误差都随侧边界输入时间间隔的增大而增大,侧边界输入间隔6 h时,误差最小。由此可见,在气候模式中对侧边界输入时间间隔的要求并不象在短期天气模式中要求的高,但固定边界的误差最大,所以应有一个合适的边界输入时间间隔,取的太小所要求的机器性能较高,取的太大,无法反映出大模式的环流特征,也会造成较大的误差。
|
|
| 图 5. (a)无地形非绝热模式热能通量逐日误差绝对值分布特征(b)无地形有日变化非绝热模式太阳辐射5天滑动平均误差(c)无地形有日变化非绝热模式动能含量5天滑动平均误差 | |
2.3 平流相速误差对嵌套误差的影响
用差分方程式代替微分方程会造成相速度的误差,这种相速度的误差与网格距有关,而大小模式嵌套时网格距的差异,会造成大小模式对同一系统模拟的不同,这就是平流相速误差对嵌套误差的影响。下面我们通过试验3来尽可能细致分析相速误差的特点及对嵌套误差的影响。
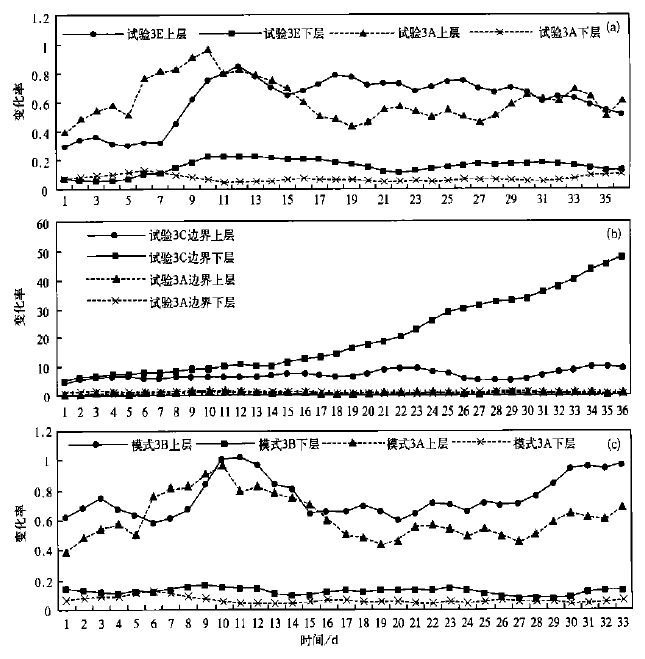
众所周知,分辨率越高,差分方程越接近微分方程,此时相速误差也就越小,所以用环圈细网格模式去模拟大气所带来的相速误差一定小于环圈粗网格模式所带来的相速误差,但区域细网格模式是否优于环圈粗网格模式,即区域细网格是否有必要性呢? 我们选取环圈细网格模式(模式3D)为参考场和背景场,来比较区域细网格模式误差(模式3A与环圈粗网格误差(模式3E); 从图 6a 来看,区域细模式的动能场上层误差在开始13天左右要大于环圈粗模式动能场上层误差,从15天左右,情况相反,环圈粗模式动能场上层误差稍稍大于区域细模式动能场上层误差; 而下层误差,环圈粗模式动能场下层误差要大于区域细模式动能场下层误差。由于一般来说,上层大气气流比较平滑,主要为长波,而在下层大气中波动较多,短波能量较多,所以由以上分析我们可以看出,细网格有限区模式在模拟上层长波大气时,不如环圈粗网格模式模拟的准确,而细网格有限区模式在模拟下层短波大气时比环圈粗网格模式要好得多,由此说明了气候有限区模式预报的必要性。但相速误差对嵌套误差的影响到底有多大呢? 同样选取环圈细网格模式(模式3D)为参考场和背景场,来比较区域细网格模式误差(模式3A,认为没有相速误差)和区域粗模式误差(模式3C)。由图 6b 看到,在边界,粗网格模式下层误差比细网格模式下层误差大得多,且随时间有增长趋势; 而在上层,粗网格模式误差也比细网格模式误差大,但并不像下层明显,在内区也可看到同样的现象(图略); 在前面的嵌套误差分析中已指出,在边界,上层误差大于下层误差,而这里,粗网格模式误差分布已变为下层误差大于上层误差,可见,相速误差对嵌套模式误差的影响主要表现在模式下层,即对短波的影响较大。上面两种均是理想情况下的相速误差,为了比较较为实际情况下的误差特点,我们仍取环圈细网格模式为参考场,比较由环圈粗网格模式提供侧边界资料的有限区细网格模式(下称模式3B)的误差及由环圈细网格模式提供侧边界资料的有限区细网格模式(下称模式3A)误差。在试验中发现,模式3B的稳定性不如模式3A的稳定性好; 模式3B的误差在上层和下层都要大于模式3A的误差(图 6c); 所以较为准确的背景场提供侧边界时区域模式嵌套误差显然较小,且随积分时间的增长,这种效果更明显。从这里也可看出,嵌套误差的某些误差来源是不能靠加强平滑或张弛区的调节来解决的,只有靠全球细网格模式加以解决。
|
|
| 图 6. 无地形干绝热模式动能场误差绝对值5天滑动平均分布(a)环圈粗网格模式与区域细网格模式误差比较,(b)区域细网格模式与区域粗网格模式误差比较,(c)不同分辨率侧边界资料造成的区域模式误差比较 | |
2.4 非绝热加热过程中有无日变化的误差比较
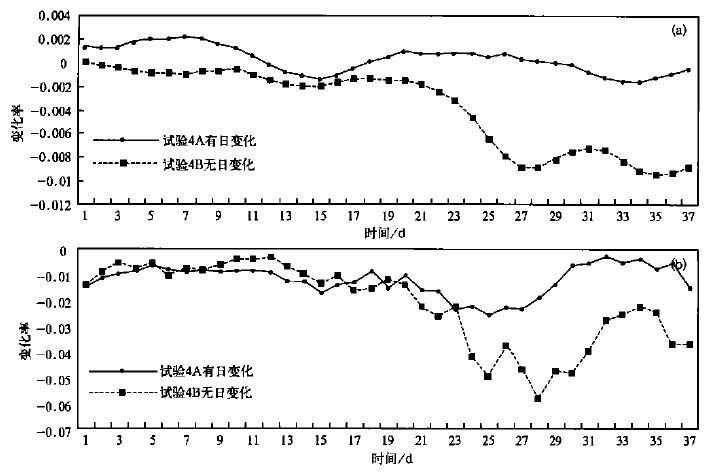
在模式的非绝热处理中,太阳辐射日变化处理不当就有可能在边界附近造成虚假的冷暖平流,而虚假的冷暖平流会导致饱和比湿的变化,产生虚假的降水源或汇。这里我们选取有日变化处理的无地形非绝热模式(模式4A)的误差与另一种极端情况即无日变化的非绝热模式(模式4B)的误差相比较,看看有无日变化对嵌套误差的影响。对于感热误差和水汽误差(图 7) ,无日变化的模式误差明显比有日变化的模式误差大,且随时间增长有增长趋势,即长期积累误差较大; 所以无论是短期天气预测,还是气候模拟中日变化的处理都是影响嵌套误差的重要因素之一。
|
|
| 图 7. 侧边界输入间隔6 h无地形非绝热模式5天滑动平均的温度(a)和水汽通量(b)误差分布 | |
3 结论
本文设计环圈模式与有限区模式进行同模式嵌套,以环圈模式预报作为参考场,设计了多种试验方案,分析了有限区模式嵌套误差的时空分布特点及不同条件下的嵌套误差。初步分析得到以下主要结论: (1) 长时间积分中,动能场误差主要在边界上层的流入区,感热场误差在边界上层较严重,水汽误差主要在边界上层的流出区,降水误差主要在内区; (2) 嵌套误差和侧边界资料输入时间间隔有关,固定边界的误差很大; (3) 有限区细网格模式在模拟上层大气长波时不如粗网格环圈模式效果好,但其在模拟下层短波时误差比粗网格环圈模式的下层误差要小,嵌套误差的大小和大小模式的网格距之比有关,且主要影响下层大气; (4) 日变化的处理是影响嵌套误差的主要因素之一,无日变化的模式误差比有日变化的模式误差要大的多。
从上面的分析中,我们对嵌套误差特征有了一个大致的了解,根据这些误差分布特征,可采用相应的方法以尽量减少误差,如根据许多物理量的误差主要分布在上层,如感热场、动能场和水汽的误差等,且细网格有限区在上层大气的模拟不如粗网格环圈模式模拟的效果好这些特征,若用三维嵌套的方法,即在模式上层也每隔一段时间用大模式的值加以调节,则应该可以减少许多由上层大气带来的误差。嵌套误差的大小和侧边界资料输入间隔有关,且对于不同的积分时间,侧边界输入时间间隔也就做相应的改动;
还需指出的是,这里所采用的误差诊断工具有其一定的局限性,它只是从动力学方面对误差进行诊断,不能从天气学方面加以分析; 若要对嵌套误差有更全面细致的了解分析,还需从天气学方面出发用其它方法进行误差诊断。这些工作以后将再做进一步的研究。
| [1] | 曾庆存, 李荣风. 不等距差分格式的计算紊乱问题. 大气科学, 1982, 6, (4): 345–354. |
| [2] | 廖洞贤, 陆维松. 有限区域预报中的一些问题. 气象学报, 1982, 40, (4): 387–397. |
| [3] | 颜宏. 单向影响嵌套侧边界技术的研究(一) 研究现状和C型跳点网格模式侧边界方案的设计. 高原气象, 1987, 6, (2): 192–204. |
| [4] | Anthes R A, Kuo Y H, Hsie E Y, et al. Estimation of skill and uncertainty in regional numerical models. Quart J Roy Meteor Soc., 1989,115: 763~806. |
| [5] | 刘永强, 丁一汇. 区域气候模拟研究. 应用气象学报, 1995, 6, (2): 228–239. |
| [6] | 苗峻峰, 徐祥德. 气候模式一重、二重区域嵌套方案的试验研究. 气象科学, 1993, 13, (3): 269–280. |
| [7] | 颜宏. 复杂地形条件下嵌套细网格模式的设计(一) 数值模式的基本原理. 高原气象, 1987, 6, (2): 1–62. |
| [8] | 颜宏. 复杂地形条件下嵌套细网格模式的设计(二) 数值模式中次网格物理过程参数化. 高原气象, 1987, 6, (2): 63–138. |
 2004, 15 (2): 152-161
2004, 15 (2): 152-161


