多普勒天气雷达是一种新型的相干雷达,它能够提供径向速度等风场信息,因而成为探测和研究中小尺度天气系统的有力工具。随着数值天气预报模式的不断发展,多普勒雷达资料这种非常规观测资料如何用于数值天气预报中是亟待解决的问题。
理论上要获得三维风场的结构,至少需要三部多普勒雷达同时进行观测[1]。在20世纪70年代发展起来的双多普勒雷达探测技术[2],利用两部雷达同步观测,测得两个相对于不同原点的径向速度场,获得风的两个分量,然后引入连续方程,求得三维风场。这就要求多普勒雷达的探测区相互重叠,增大布网密度,就目前的情况,难以实现。因此单部多普勒雷达反演就被提到实际应用日程上来。本文着重研究单部多普勒雷达资料的四维同化。
由于高原、沙漠、海洋地区的常规观测站非常稀少,所以全球的数值预报仅靠常规观测资料很难分析出准确的初始场。随着雷达、卫星等各种非常规观测资料应用的迅速发展,极大改善了全球范围的资料状况。如何有效的利用各种不同时次不同类型的观测资料,改进客观分析的质量和数值预报的初始场,这就是资料同化需要解决的问题。资料同化包含以下两层基本含义:(1)如何合理利用各种不同的非常规观测资料,把它们与常规观测资料融为一个有机的整体,提供更好的初始场;(2)如何综合利用不同时次的观测资料,将这些资料中所包含的时间演变信息转化为要素场的空间分布状态。多普勒雷达资料四维同化是20世纪80年代末发展起来的一种全新的四维同化方法。这种方法将动力约束与资料约束以及不同时刻的一切观测资料(包括常规资料与非常规资料、模式变量资料与非模式变量资料)同时考虑,依据变分原理与共轭方程理论,利用同化时段内多时次资料中所包含的时间演变信息,求解出一个最优的初始条件。这种最优初值既与数值模式相协调,又能使同化时段内的模式预报值最大限度的符合实际观测值。数据同化技术在单部多普勒雷达观测数据上的应用是很有意义的。多普勒雷达资料数据同化对于风暴预警、现时预报、航空业务以及数值天气预报中非常规观测资料如何有效应用于数值模式等,都有重要的意义。
多普勒雷达资料同化的出现时间不是很长,在较短的时间之内得到了很大发展。Gal-Chen 于1978年首次提出了将多普勒雷达数据应用到滞弹性模式反演出压力和热动力值[3],该方法使用了Navier-Stokes 方程的简化形式,即滞弹性近似的动量方程和连续方程;随着计算机计算能力的提高,80年代末Lewis 等提出四维变分数据同化[4][5],之后Wolfsberg 等人也提出该方法,他们使用Boussinesq 模式和模拟过的边界扰动数据[6][7],这是将伴随方法首次用于气象数据同化的例子之一。Sun 等人于1994年改良了多普勒雷达四维变分分析系统(4D-VDRAS:four-dimensional variational Doppler radar analysissystem)[8],并用阵锋风观测资料进行了检验,得到了比较好的效果。进而他们又用该系统反演对流风暴云体的动力和微物理过程。1997 、1998年Sun 等人的研究表明VDRAS能够反演出三维风场、热动力场等[9][10]。Wu 等人将该系统应用到超级单体风暴云中[11],该系统可以反演出风暴结构的所有比较明显的特征。
随着雷达资料反演技术的提高,应用这种高分辨率的数据预报风暴结构的演变和发展技术也得到不断发展。Weygandt 、Gao 等人应用单多普勒雷达资料的反演数据对中尺度数值模式初始化[12][13],尽管细节上还存在很多问题,但结果还是颇令人鼓舞的。
1 基本原理假设作用在空气团上的力的总和在一个同化窗口内保持不变。
多普勒雷达资料四维同化的过程中要寻找各个空气团上初始风场结构和作用力,从而使得在同化窗口内,沿着轨道方向上预报的径向风场和观测所得到的径向风场之间的差异达到一个最小值。
根据牛顿运动力学,大气空气微团的水平运动方程可以简写为:
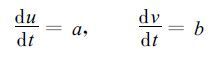
|
(1) |
d/dt表示时间变化率;u,v是笛卡尔坐标中的水平速度分量;a,b分别是x,y方向单位质量的作用力。若x,y方向上的初速度为u0,v0,气团在x,y方向上的初始坐标为x0,y0,在一个同化窗口内,假定a,b为常数,所以有

|
(2) |

|
(3) |
在极坐标内,设r0为初始矢径,r为径向矢量,vr0,vΦ0分别为初始径向速度和初始切向速度,二者互相垂直,Φ为方位角,以正北为零,顺时针方向增加,依照式(2)和(3)以及:r2 =x2 +y2,r0vr0=x0u0+y0v0,u02+v02=vr02 +vΦ02,则有:
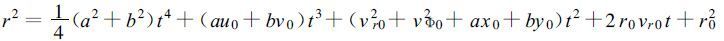
|
(4) |
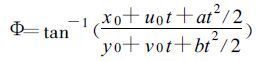
|
(5) |
同时,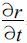
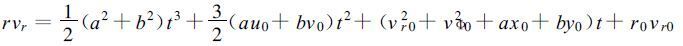
|
(6) |
由坐标之间的关系,可得到两种坐标情况下初始值的关系:

|
对于a,b,vΦ0的取值,应该遵循一个原则:它们所取的值应该使得在一个同化窗口内所得到的观测值和理论值的vr之间的差异达到最小。
式(6)表示多普勒雷达对一个空气微团的连续观测值r0,vr0,r,vr之间的关系,当a,b,vΦ0确定后,该关系将完全确定。在同化时段内取定a,b,vΦ0的值,使得观测值和实验反演值之间的差异达到最小。
即:
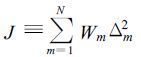
|
(7) |
达到最小。
其中Wm=W(tm)是一个实时的权重函数。
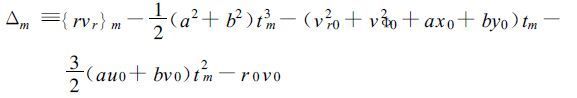
|
(8) |
该式表示试验值rvr和观测值{rvr}m之间的差异。在笛卡尔坐标系中,{rvr}m≡rvr(x(tm),y(tm),tm);在极坐标系中,{rvr}m≡rvr(r(tm),Φ(tm),tm)。方程(7)称为价值函数。
四维变分同化作为数值天气预报的反问题,其目的在于寻找一个既和动力模式相协调又能使同化时段内的预报值与观测值充分接近的初始场。式(8)表示同化窗口内模式预报值与观测值之间的差距,有些文章中也将其称为目标泛函[14]。
现在的关键问题是如何使同化窗口内模拟值与观测值之间的差异达到最小,也就是价值函数J 达到最小,这是四维同化的核心问题。可以先给出a,b,vΦ0的初始猜测值,然后寻找一个沿着J(a,b,vΦ0)的最大下降方向的路径,找到Jmin。
有关J 的最小值问题,其解决方法有最陡下降法、牛顿下降法、共轭梯度法等。这些方法的大体思路都是通过在下降方向上不断迭代,直到出现可以使价值函数J达到最小值的一组(a,b,vΦ0)出现,这时的(a,b,vΦ0)就是需要的最优解。目前寻求最小值的常用方法是共轭梯度法,即建立如下的迭代格式:Y0k+1 =Y0k+ρkdk,Y0为数值预报的初值,dk,ρk是与Y0维数相同的矢量,前者为下降方向,后者为下降方向的步长,将上式不断迭代,合理选取dk的共轭方向及相应的步长ρk,逐次迭代,使Y0k不断逼近最优解。
上述方法的基本思想是把大气运动的演变看成是(a,b,vΦ0)的函数,在实际应用中,可以包括初始条件、边界条件和模式参数,把大气运动方程做为算子,各时刻的大气运动状态是该算子对初始场的一种映射,而式(7)所定义的价值函数J 是初始场的泛函。在应用到具体的动力模式中时,将动力模式和同化窗口内的所有观测资料作为约束条件,通过不断调整初始条件使价值函数达到最小,从而获得四维同化气象观测资料和最优的初始场,即将四维同化和数值模式初值的形成作为一个统一的整体来考虑。对多普勒雷达资料来说,还存在资料如何放入的问题。这些资料必须反演转化为模式变量后才能进行客观分析,而反演转化过程中不可避免会产生误差,这可能导致雷达反演资料的品质远不及常规资料。但目前国际上正在大力研制发展的四维变分同化方法,能够充分利用多时次资料中所包含的时间演变信息,可以对各种非模式变量进行同化,从而有效解决上述问题。这种方法对计算速度和存储量的要求很高。随着计算机和计算技术的发展,多普勒雷达资料四维变分同化在实际业务中得到应用,将对数值预报产生极其深刻的影响。下一节中将着重讲述4D-VDRAS 问题。
2 多普勒雷达资料四维同化的基本方法 2.1 基本算法 2.1.1 4D-VDRAS 数值模式的四个预报方程Sun 和Crook 在2000年应用多普勒雷达四维变分分析系统(Four-Dimensional VariationalDoppler Radar Analy sis Sy stem:4D-VDRAS)做循环过程[15],即将前一次循环所得到的结果作为下一个循环的初始猜测场和背景场。它具有实时预报的效果,能提高预报的准确性。4D-VDRAS 用来同化一系列的单或多多普勒雷达观测资料,用云尺度的数值模式来描述大气运动的演变状况。
设大气在某一高度上为固体边界面,其面与地面之间的距离比干绝热大气的密度的标高小,在这种假设下,大气可压缩性影响可以忽略,干燥的浅对流状态下,得到Boussinesq近似,即数值模式所包含的四个预报方程为:
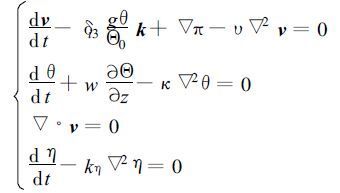
|
(9) |
该式没有考虑湿过程问题。式中,v表示速度矢量,k为垂直方向的单位矢量,π是扰动气压,θ是扰动位温,Θ是水平平均位温,Θ0是相当位温,η是雷达反射率,其单位是dBz,Φ是涡动粘滞系数,κ是热扩散系数,kη是反射率扩散系数,这些系数是恒定的。式(9)中的第一式为大气动力学方程,其中扰动气压满足三维泊松方程:
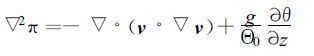
|
(10) |
第二式为热力学方程,第三式为连续方程,第四式为雷达回波反射率的守恒方程,它是在假设同化时段内,反射率的源汇项忽略不计的条件下成立的。
2.1.2 价值函数(1) 价值函数的定义
价值函数的定义为:
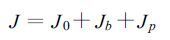
|
(11) |
其中,J0表示雷达观测数据与相应的模拟数据的差异,Jb是背景项,Jp是时空平滑项。
(2) 观测资料价值函数J0
J0的一般表达式为:
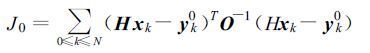
|
(12) |
其中k是时间序号,xk是状态向量,yk0 是对应的观测矢量,H是观测算子,O是误差协方差矩阵,它包括观测误差和观测算子误差。xk,yk0可以表示不同格点上的不同变量值,观测算子H既代表与观测变量(如径向速度vr等)相关的模式变量(如u,v,w等)的分析泛函,又代表不同格点之间的传递过程。
假定观测资料的误差是不相关的,则一般情况下O的作用经常忽略,所以式(12)又可以定义为:
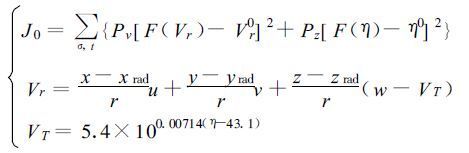
|
(13) |
其中第一个式子里的Vr0,η0 分别代表从多普勒雷达观测得到的径向速度和反射率,Vr,η是模式模拟值,F表示雷达资料和模式变量之间的格点转化泛函。两个P值代表径向速度和反射率的权重系数,一般Pv=1 ;Pz=0.5,σ、t代表空间和时间;第二个式子中,r是模式格点(x,y,z)和雷达测点(xrad,yrad,zrad)之间的距离,VT是雨滴下落末速度;第三个式子中,η是雷达反射率,单位是dBz。
(3) 背景场价值函数Jb
它用来估计由当前预报的误差,定义如下:
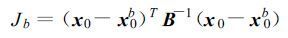
|
(14) |
x0是当前分析值,x0b 是相应背景状态矢量,B是背景场误差协方差矩阵,它可以通过寻找真实的大气状态场(true)和相应的背景分析场(background)之间差异的期望值来得到:
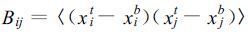
|
(15) |
使用动力模式还使各分析场有了一定的相关性,所以可以采用相对简单的相关模式来平滑自由噪声。因为垂直方向的作用很小,所以相关模式一般只考虑水平结构,忽略垂直相关。
定义
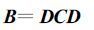
|
(16) |
D是对角矩阵,表示标准差,它可以通过多普勒雷达观测得到的径向速度估计出来。C是误差相关矩阵。C中各元素的值可以定义为:
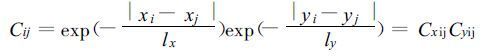
|
(17) |
这样定义的好处是使得x,y分离,从而C的转置矩阵相对好求。应用克罗内克乘积,有:
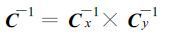
|
Cx-1,Cy-1的平方根可以通过一个单一的矢量分解得到,并可以截断成为带状矩阵Fx,Fy。所以,背景场价值函数Jb可以表示为:
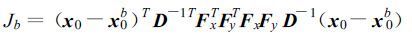
|
(18) |
B=D-1 TFxTFyTFxFyD-1,这部分相当于一个回归过滤网。
(4) 价值函数的时空平滑项
众所周知,若在数值模式连续积分过程中,在一定时间间隔加入与模式积分时刻一致的多普勒雷达观测资料来直接取代预报值,则会引起所谓的重力波冲击。由于无论是预报值还是观测值都不可能是完全准确的,二者之间的不协调必然会不断激发出重力惯性波,这就需要做一定的平滑处理,所以价值函数的时空平滑项定义如下:
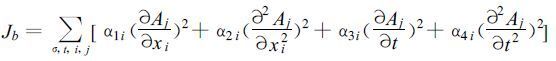
|
(19) |
Aj代表模式变量,xi代表空间量(x,y,z),t代表时间,α是权重系数。权重系数是由尝试法得出的。Sun 等人2000年用WS R-88D 资料试验中,权重系数设置如下:α3,α4对于雷达资料反演得到的水平速度(u,v)分量取0.005,而垂直速度w和温度T取0.01,α1,α2在边界处取相同的值,对应其它变量时为0。
2.1.3 价值函数的最小值(1) 基本原理
对于VDRAS,在求J的最小值时,要先求出J对于各个约束变量的梯度。基于共轭方程理论的伴随方法可以有效解决这一问题。
为简要起见,设在Hilbert 空间中,大气运动方程的形式为:
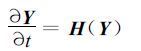
|
(20) |
H是Hilbert 空间的线性算子,那么,该方程的离散形式(即同化模式)可写为:
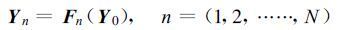
|
(21) |
Yn是M维(M为模式变量和网格点数的乘积)的向量,代表在时间tn的模式状态。
相应的价值函数定义为:
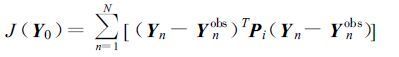
|
(22) |
其中Y0为数值预报的初值,如风速、温度等,而Ynobs 是对应的观测值,Pi表示权重系数。
对于大气运动方程组及价值函数方程取变分,并利用Hilbert 空间中的泛函性质可知:
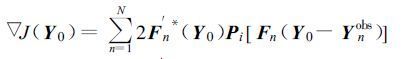
|
(23) |
对Fn求导并在该空间中取共轭,得到Fn′* (Y0)。
由该式可见,价值函数的梯度与模式预报的初值和同化窗口内对应的观测值Y有关。但是由于数值模式的复杂性,直接由该式求出J的梯度是不可能的,所以必须加入一种计算复杂变量符合函数梯度的数值方法,即伴随方法,通过反向积分伴随模式计算价值函数的梯度。
将式(20)取变分δY,并写出共轭方程形式,有:
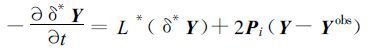
|
(24) |
L*是共轭算子,δ*Y是δY的共轭函数。
在实际工作中,将式(24)写为便于求解的离散形式,即为伴随模式。但是描述大气运动的模式方程很复杂,而且实际大气模式中还包括很多特殊处理过程,所以按以上方法先写出共轭方程,再构造出相应的伴随模式几乎是不可能的。在目前的变分同化研究中,大都采用程序码转置法,直接从数值预报模式的程序码入手,把某段程序看成是一个泛函算子,然后利用共轭转置的办法,导出伴随算子,再写成相应的伴随模式的程序码。
所以,四维变分同化的计算流程可总结如下:
① 确定数值模式中各控制变量的初始猜测值Y00,并在同化窗口内对同化模式正向积分,得到各个时刻的Y00,保存。
② 将Yn0带入大气运动状态方程的共轭方程,反向积分相应的伴随模式方程;
③ 写出并计算价值函数,求其对于各个控制变量的偏导;
④ 利用下降算法确定价值函数的下降方向:
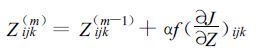
|
α是根据最佳控制原理得到的最优步长[16],m为迭代次数,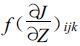
⑤ 察看是否 Jm-Jm-1≤δ,若满足,则输出此时的Ym0,结束;
⑥ 若上一步不满足,重复②~⑤步骤。
(2) 具体算法
雷达资料伴随算法的主要思想如下:①使用多普勒雷达观测得到的反射率/径向风场资料反演时间平均风场,使用连续的时间序列资料减少反演过程中的不确定性;②联合其它与多普勒雷达观测资料无关的方程,如连续方程等作为弱约束项,加入到反演过程中;③边界条件相对容易得到,因为在守恒方程方面只有反射率/径向风的贡献。
关于多普勒雷达资料的伴随反演问题,有许多方法,如全伴随,简单伴随等。目前较常用的三维简单伴随方法,即3D-SA(three dimensional simple adjoint)。Xu 于1994年用Phoenix Ⅱ的实验数据对该方法做了检验[17~20],表明该方法可以对雷达不能观测到的大气结构状况作出较好的反演,同时对于数值模式的初始化也有很好的提高。
在3D-SA 方法中,首先给出所需要解决问题的价值函数的具体形式,然后计算它对于各个控制变量的偏导,联合伴随模式,求出最小值。Xu 等人利用径向风速的动量方程和反射率的平流方程作为控制方程,在控制方程中选择控制变量,用最优控制的方法迭代。
设柱坐标系(r,α,z)的原点在雷达处,则径向风速的动量方程是:
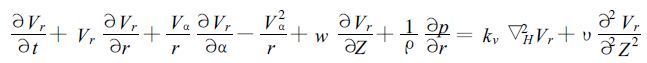
|
(25) |
水平风矢V=(Vr,Vα),w是垂直风速,p为气压,ρ为空气密度,▽H2 是柱坐标系的拉普拉斯算子,kv为径向速度的水平涡动粘滞系数,Φ为垂直涡动粘性系数。
对于一个反演时段τ,水平风速可以分解为两部分:时间平均部分Vm和脉动部分V′,Vm=(Vrm,Vαm),V′=(Vr′,Vα′),V=Vm+V′。这样式(25)还可写为:
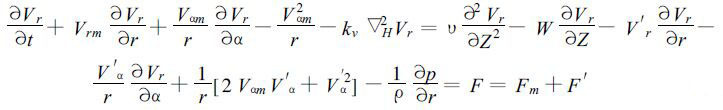
|
(26) |
在一段时间内取平均,强迫项的扰动项可忽略,则上式可写为:
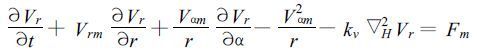
|
(27) |
Fm为强迫项的平均值。
相应的边界条件为:
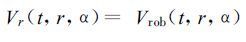
|
(28) |
相应的初始条件为:
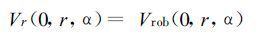
|
(29) |
式(27)至(29)即是SA 方法的速度控制方程。
同理,在柱坐标系中相应的反射率的平流方程为:
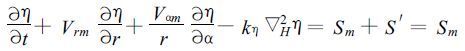
|
(30) |
η为反射率,kη为反射率的水平涡动扩散系数,Sm为强迫项的平均值。相应的边界条件为:
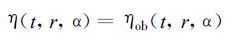
|
(31) |
相应的初始条件为:
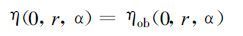
|
(32) |
式(30)至(32)即是SA 方法的反射率控制方程。
控制方程中的控制变量为(Vm,Sm,Fm,kv,kη)。在反演时间τ内,给出最佳的“预报值” η,Vr,使下式定义的价值函数最小:
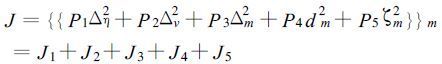
|
(33) |
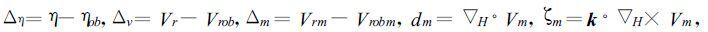
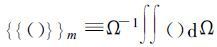
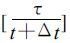
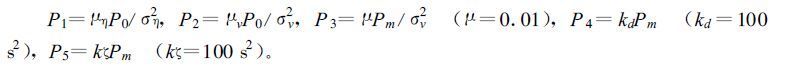
|
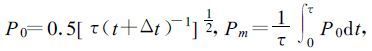
由式(33)可见,J1代表了反射率的预报值和观测值之间的差异,J2是相应的径向风速预报值和观测值之间的差异,J3代表了反演风场和观测的时间平均风场之间的差异,它对应的是反演的时间平均径向风场,是一个弱约束项[21],而J2是径向风反演与观测之间的差异,属于强约束项,二者在整个价值函数中的作用不同。后两项J4,J5是相对于反演的水平风场的弱辐散和涡旋约束,其本质是平滑约束。
对Vr所对应的三个控制方程取变分,即对式(27)、(28)、(29)取变分:
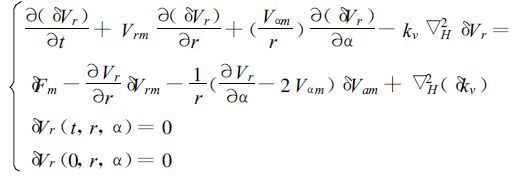
|
(34) |
同理,对η所对应的三个控制方程取变分,即对式(30)、(31)、(32)取变分:
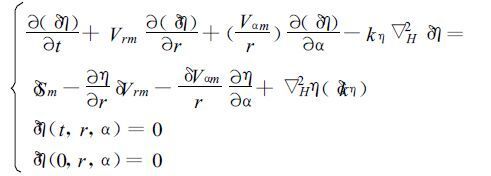
|
(35) |
利用Hilbert 空间性质写出状态矢量的共轭算子,η*,Vr* 是相应的伴随模式的共轭算子,则控制方程Vr的伴随方程和初始边条件为:
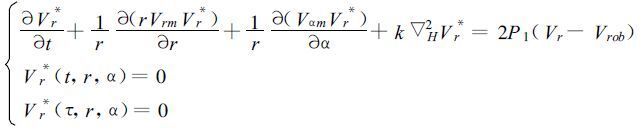
|
(36) |
控制方程η的伴随方程和初始边条件为:
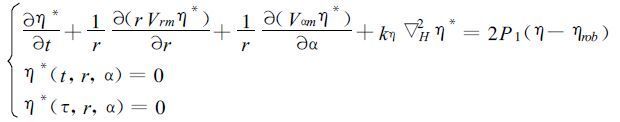
|
(37) |
价值函数相对于各个控制变量(Vm,Sm,Fm,kv,kη)的梯度为:
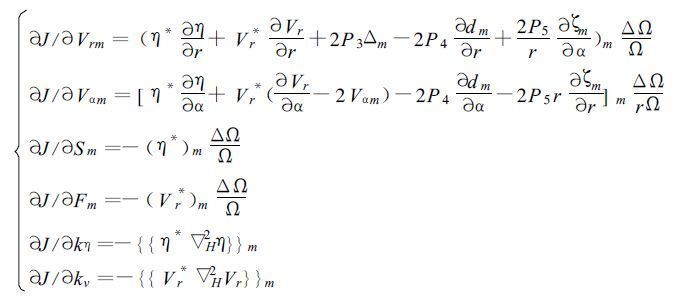
|
(38) |
该式的推导过程略。Δm,dm,ζm,{{}}m的含义如前,()m≡τ-1∫0τ(),是时间平均算子。ΔΩ=rΔrΔα,代表柱坐标系中的格点面积元。
采用共轭梯度法,确定出价值函数相对于各控制变量的最佳下降方向,不断迭代,存储每一次的(Vm,Sm,Fm,kv,kη)值,使得相应的 Jm-Jm-1≤δ,则是最佳(Vm,Sm,Fm,kv,kη)值。输出该值,同化过程结束。
关于该过程的误差,只做简单的理论分析。式(27)、(30)是通过略去其脉动部分得到的,这自然会产生误差;且Vrob等也必然包括观测误差;另外,价值函数J的权重系数的取值也有很大的经验成分。
(3) 预处理原理
对于价值函数最小值取得的方法已经有很多改进,这里简单介绍一种预处理算法。预处理算法实际上是一种嵌入式的最小值算法[22],其目的是为了在4DVAR 中减少价值函数耦合到最小值过程中的迭代次数。通过预处理,可以大大提高多普勒雷达四维变分同化的运算效率。预处理算法依赖于所估算的价值函数的递减和计算出的梯度模方的比值,二者均定义在模式空间内。预处理参数定义为:
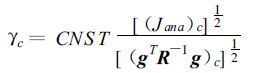
|
(39) |
CNST是试验确定的参数,g表示梯度,Jana表示定义在模式空间内的价值函数,R是对角矩阵,下标c表示模式的子空间。在每一个垂直高度层和对每个变量,按照计算预处理系数的思路,应考虑地面气压、各层的温度、风和比湿。
预处理矩阵P-1中的元素是由P-1 =ΓR-1得到的,Γ是一个表值为γc的对角矩阵。
在同化过程中如果直接同化观测资料,则需要有一个空间转换的泛函问题:式(39)是定义在模式空间中的,而直接观测部分的目标泛函是定义在观测点上的。这就需要做泛函上的处理。在两个Hilbert 空间之间定义一个闭合、有界的线性算子S,由数学性质知:
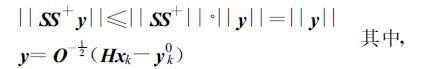
|
S+是S的伪逆矩阵[23]。x,yk0,O,H的意义如前式(12)。而S、S+等幂正交,因此有:
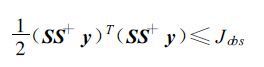
|
令:
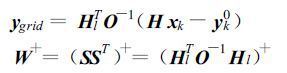
|
(40) |
Hl为H的线性算子。则可以在模式空间上定义一个价值函数J,有
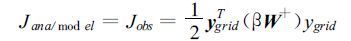
|
(41) |
ygrid定义在模式分析空间,而不是在观测点空间。β ≥1,是一个标量,它包括了在所给时次的所有可利用的观测值,对于多普勒雷达来说,就是反射率和径向速度。这就完成了一个空间转换。
利用预处理算法,仅仅需要20~25次重复就可使价值函数达到最小值,在业务应用中,这个次数还会进一步减少。
2.2 观测资料的质量控制多普勒雷达资料在做同化之前需要进行客观分析与质量控制。客观分析是把不规则的观测资料值,插值到规则网格点上;质量控制就是对观测数据进行检查。
对错误的记录加以订正或剔除,这种初步的处理工作对于提高分析质量和预报准确率是十分必要的。如WSR-88D Ⅱ,数据的方位分辨率是1°,径向速度分辨率是250 m,反射率是1 km。数据的水平分辨率比相应的模式格点高很多,所以在4D-VDRAS 中应用雷达资料之前,首先在1 km 的笛卡尔坐标中进行质量控制,然后在水平方向上插值到更大的模式格点中。
为了把近地面扰动和不规则回波扰动所产生的噪声数据去掉,对于雷达所得到的径向速度值小于0.25 m/s 的数据滤掉。通过计算,还要把那些偏离平均值很多的虚假回波数据剔除。
在4D-VDRAS 过程中,尽管理论上可以把边界层状况作为控制变量对之进行反演,但实际上,由于雷达数据的不充分,要做到这一点是困难的。因此,数值模式的边界状况一般是先指定好的;垂直速度在顶、底的边界状况设为0。潜热在边界处无扰动。在边界格点上如果没有可利用观测资料,则中尺度分析的风场反演结果就用来弥补该缺漏。
2.3 中尺度分析及插值原理鉴于多普勒雷达探测能力所限,在动力模式区域中可能出现资料空缺的情况。这就需要用背景场估计结果来填补这些空缺,给出价值函数最小值的初始猜测场。侧边界情况也需要背景场的资料估计。背景场的估计是通过VAD 技术和中尺度分析来完成的。
在多普勒雷达资料四维变分同化系统中,使用了两种VAD 技术:一是恒定仰角的VAD 技术;二是恒定范围的VAD 技术。Sun 和Crook 等采用第二种方法。
中尺度分析需要使用大量的非常规观测资料,如雷达、卫星、飞机等观测资料,所用的分析方法和采用的参数都必须考虑到中尺度天气系统的特征。其特点是时空分辨率高,分析的气象要素和物理量随时空的变化率大,不满足地转平衡等约束关系,对一些强烈天气系统,静力平衡关系也不适用。通过中尺度分析,能够深入的探索一些短期内造成严重灾害的强烈天气系统的物理特征和成因,有效的做出中尺度天气预报。
气象场的中尺度变化是对大尺度变化的一种扰动,而直接从观测到的气象要素场中将其辨认出来是很困难的,所以要想反映这种扰动天气系统,就必须设法将它从气象要素场中分离出来。
在这里介绍一种中尺度系统的分离方法,即Barnes 插值技术[24]。这是一种将不规则测站资料转换为网格点资料的客观分析方法同尺度分离方法相结合的一种技术。
具体方法是运用一个低通滤波器过滤原始资料,首先计算低通滤波场的初值F0(i,j)。假定F的观测是连续的,对任一网格点(x,y),各测站与其距离为rn,则有:
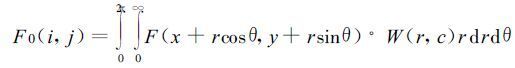
|
(42) |
其中W =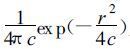
众所周知,多普勒雷达观测资料的分辨率比相应的数值模式的分辨率高一个量级左右,所以把数据直接插值到笛卡尔坐标中就会出现较大的误差;雷达资料的垂直分辨率较水平分辨率低,所以可以考虑直接同化PPI 数据:如果直接对极坐标格点上的原始雷达数据进行同化操作,那么所需的计算量就非常大;若将一定仰角层上的数据从极坐标格点插值到笛卡尔坐标格点上,可减少计算量,自此将插值过的PPI 资料作为观测资料。
因为输入的PPI 资料是连续仰角层的,所以价值函数中的算子就必须包括从模式格点到数据格点中各变量的转换,使其二者之间的差异可以通过价值函数表现出来。依据雷达原理,下述关系式可完成数据从模式垂直层面到抬升仰角层的转变:
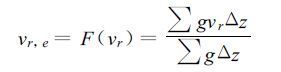
|
(43) |
vr,e表示某一仰角层上的径向速度值,Δz是模式垂直格距,z是到雷达波束中心的距离,g 代表雷达天线获得回波的能力,g=e-z2/(2β2),β 是雷达波束宽度的一半。
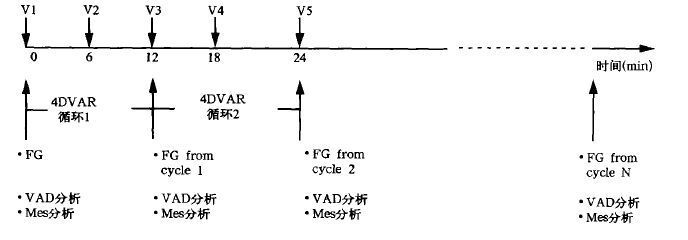
2.4 运行方式VDRAS 采用循环过程。设每个同化窗口的时间是12 min,则其过程如图 1所示。该图中,FG 表示初始猜测场(first guess),V(1,2,……)表示从多普勒雷达所得到的体扫观测数据,Time 轴表示同化的时间窗口走向,VAD 分析和Mes 分析用来进行辅助分析。在每个小过程中,数值模式正向积分,计算价值函数;伴随模式反向积分,计算价值函数的梯度。然后计算价值函数的耦合点,用 Jm-Jm-1≤δ来判断。δ是允许的误差值,m表示该过程需要重复的次数。研究表明,m一般取在30至50之间。
|
|
|
图 1. VDRAS 循环过程示意图
|
|
3 4D-VDRAS 的应用 3.1 在云物理研究和风暴预报中的应用
当有降水过程时,通过雷达的反射率资料就可以显示出降水中的水汽凝结物状况。对于降水观测资料来说,将多普勒雷达反射率转换为雨水混合比qr,可以采用Sun 等人提到η-qr的关系。若η的单位是dBz,则有:
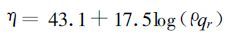
|
(44) |
ρ为空气密度。有了这种关系,在式(13)中的第一个关于价值函数的表达式中,就可以将η用qr来代替,把qr直接作为观测资料来用。
对水汽凝结物观测资料进行同化,需要调用云模式作为整个模式运行约束中的一部分,但因为在气象场微物理过程中的不确定因素很多,所以该过程还有很大的困难。
首次将VDRAS 应用到水汽凝结物四维同化的是1997年Sun 和Crook,次年他们又将该方法应用到实践。研究过程中他们将一个风暴云团作为观测对象,将反演得到的热动力场和微物理场与飞机的观测资料相对比,结果两者比较一致。1999年Wu 等人采用三部多普勒雷达,每个体扫历时3 min,进行四维同化试验,同化窗口为6 min。所有体扫资料的反演试验表明,微物理场和动力场都和雷达的观测基本吻合,但风暴量级减弱;2000年Warner 等人应用4D-VDRAS 反演1996年一次特大降水过程发现[25],对风暴的预报只能维持2h,两小时之后与事实的相关性迅速减弱。
2001年,Sun 和Crook 又将VDRAS 应用到单多普勒雷达观测到的超级单体风暴云中,他们发现,对风暴云体2 h 之后的预报与低层的湿度和平均风向很有关系。其主要实验结果可以总结为两条:风暴预报的敏感性和环境的低层湿度以及可利用的径向风场资料有很大的关系;在风暴云体的生成和发展阶段,同化多普勒雷达观测的径向速度资料起了决定性的作用,但是环境场低层湿度的影响在云体的生成阶段的作用更加明显。
3.2 4D-VDRAS 在中尺度数值模式中的应用将VDRAS 放到中尺度数值模式中去就目前来讲还是一个很大的挑战。中尺度过程通常和大尺度过程息息相关,单靠多普勒雷达观测资料不足以构成中尺度本身所需的数据初始化要求,因此在做这一步工作时,要联合大尺度的观测要素值。近几年的研究开始倾向于将雷达观测资料放入中尺度系统中,并估计它对中尺度天气预报的影响。
2000年,Guo Y 等人在对美国Kansans-Oklahoma 地区由15部WSR-88D 雷达和500个雨量计观测到的每小时降水资料进行了同化试验[26]。联合MM5中尺度数值模式。他们的研究表明,同化的降水资料对降水总量和降水形式都有了很大的改进,同时同化对温度的反演也有很大影响。
Michelson 和Seaman 于2000年利用以上数据,将牛顿松弛技术应用到MM5-4DVAR实验中[27],试验结果表明,对VAD 方法反演得到的风场进行同化可以明显减少模式的风场计算误差。
2001年,Xu 等人又将同化的WSR-88D 雷达观测到的径向风场和反射率资料放入MM5中尺度数值模式中[28]。使用的资料是1997年美国纽约的雪暴资料。他们使用MM5-4DVAR 来同化径向速度和雨水混合比qr。采用式(44)所示的η-qr 关系。实验表明,同化系统并不能精确的反演未观测到的模式变量,其温度场的RMS 误差在进行了50次迭代后,只减少了30 %。尽管如此,MM5-4DVAR 同化系统对于直接将观测资料插值到数值模式中去所取得结果还是很有成效的。
4 总结多普勒雷达四维变分同化的发展是非常规观测资料四维变分同化发展的重要部分。气象工作者已经进行了大量研究,但仍然存在不少问题。多普勒雷达资料四维变分同化必须利用一个完全的三维大气模式,进行多次积分、迭代,其计算量是很大的,而且对资料的要求很高,很多方面还在不断的改进中。
今后的4DVAR 发展应该从以下几个方面着手:①发展更加适合于对流尺度系统的四维同化技术;②在4DVAR 中不仅要考虑雷达资料,还要联合其它可利用的观测资料;③研究雷达资料对中尺度过程的影响;④数据的质量控制和误差估计。
| [1] | Larry Armijo, A theory for determination of wind and precipitation with Doppler radars. J. Atmos. Sci., 1969, 26: 570–573. DOI:10.1175/1520-0469(1969)026<0570:ATFTDO>2.0.CO;2 |
| [2] | Doviak R J P S, Strauch R G, Miller L J, Error estimation in wind field derived from dual-Doppler radar measurement. J. Applied. Metero., 1976, 15: 868–878. |
| [3] | Gal-Chen T, A method for the initialization of the anelastic equations:Implications for matching models with observations. Mon. Wea. Rev., 1978, 106: 587–606. DOI:10.1175/1520-0493(1978)106<0587:AMFTIO>2.0.CO;2 |
| [4] | Lewis J M, Derber J C, The use of adjoint equations to solve a variational adjustment problem with advective constraints. Tellus, 1985, 37A: 309–322. DOI:10.1111/tela.1985.37A.issue-4 |
| [5] | Talagrand O, Courtier P, Variational assimilation of meteorological observations with the adjoint vorticity equation. Ⅰ: Theory. Quart. J. Rou. Meteor. Soc., 1987, 113: 1311–1328. DOI:10.1002/qj.49711347812 |
| [6] | Wolfsberg D. Retrieval of three-dimensional wind and temperature fields from single-Doppler radar data. CIMMS Rep.84, 1987. 91 pp. |
| [7] | Sun J, Recovery of three-dimensional wind and temperature fields from single-Doppler radar data. J. Atmos. Sci., 1991, 48: 876–890. DOI:10.1175/1520-0469(1991)048<0876:ROTDWA>2.0.CO;2 |
| [8] | Sun J, Crook N, Wind and thermodynamic retrieval from single-Doppler measurements of a gust front observed during Phoenix Ⅱ. Mon. Wea. Rev., 1994, 122: 1075–1091. DOI:10.1175/1520-0493(1994)122<1075:WATRFS>2.0.CO;2 |
| [9] | Sun J, Crook N, Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. J. Atmos. Sci., 1997, 54: 1642–1661. DOI:10.1175/1520-0469(1997)054<1642:DAMRFD>2.0.CO;2 |
| [10] | Sun J, Crook N, Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. J. Atmos. Sci., 1998, 55: 835–852. DOI:10.1175/1520-0469(1998)055<0835:DAMRFD>2.0.CO;2 |
| [11] | Wu B, Verlinde J, Sun J, Dynamical and microphysical retrieval form Doppler radar observations of a deep convective cloud. J. Atmos. Sci., 2000, 57: 262–283. DOI:10.1175/1520-0469(2000)057<0262:DAMRFD>2.0.CO;2 |
| [12] | Weygandt S. The retrieval of initial forecast fields from single-Doppler observations of a supercell thunderstorm. Ph.D. 1998. |
| [13] | Gao J, Xue M, Wang Z, The initial condition and explicit prediction of convection using ARPS adjoint and other retrieval methods with WSR-88D data. AZ, Amer.. Meteor. Soc., 1998: 176–178. |
| [14] | 周毅, 刘宇迪, 等. 现代数值天气预报. 北京:气象出版社, 2002: 197. |
| [15] | Sun J, Crook N, Real-time low-level wind and temperature analysis using single WSR-88D data. Wea. And Forc., 2000, 16: 117–123. |
| [16] | Gill P E, Murry W, Wright M H, Practical Optimization. Academic Press, 1981: 401. |
| [17] | Xu Q, Adjoint-method retrievals of low-altitude wind fields from single-Doppler reflectivity and radial-wind data. J. Atmos. Oceanic. Tech., 1995, 12: 1112–1115. |
| [18] | Xu Q, Q iu, Simple adjoint methods for single-Doppler wind analysis with a strong constrain of mass conservation. J. Atmos. Oceanic Thch., 1994, 11: 289–298. DOI:10.1175/1520-0426(1994)011<0289:SAMFSD>2.0.CO;2 |
| [19] | Xu Q, Adjoint-method retrieval of low-altitude wind fields from single-Doppler reflectivity measured during Phoenix Ⅱ. J. Atmos. Oceanic Thch., 1994a, 11: 275–288. DOI:10.1175/1520-0426(1994)011<0275:AMROLA>2.0.CO;2 |
| [20] | Xu Q, Adjoint-method retrievals of low-latitude wind field from single-Doppler wind data. J. Atmos. Oceanic Tech., 1994b, 11: 579–585. DOI:10.1175/1520-0426(1994)011<0579:AMROLA>2.0.CO;2 |
| [21] | Sasaki Y K, Some basic formalisms in numerical variational analysis. Mon. Wea. Rev., 1970, 98: 875–883. DOI:10.1175/1520-0493(1970)098<0875:SBFINV>2.3.CO;2 |
| [22] | Milija Zupanski, A preconditioning algorithm for four-dimensional variational data assimilation. Mon.Wea.Rev., 1996, 124: 2562–2566. |
| [23] | Golub G H, et al. Matrix computations. The Johns Hopkins University Press, 1989. 642. |
| [24] | 中尺度天气原理和预报, 北京: 气象出版社, 2000: 189-191. |
| [25] | Warner T T, Brandes E E, Sun J, Predicition of a flash flood in complex terrain. PartⅠ: A comparison of rainfall estimates from radar and very short range rainfall simulations from a dynamic model and an automated algorithmic system. J. Appl. Meteor., 2000, 39: 797–814. DOI:10.1175/1520-0450(2000)039<0797:POAFFI>2.0.CO;2 |
| [26] | Guo Y, Kuo Y-H, Dudhia J, Four-dimensional variational data assimilation of heterogeneous mesoscale observations for a strong convective case. Mon.Wea.Rev., 2000, 128: 619–643. |
| [27] | Michelson S A, Seaman N L, Assimilation of NEXRAD-VAD winds in summertime meteorological simulation over the northeastern United States. J. Appl. Meteor., 2000, 39: 367–383. DOI:10.1175/1520-0450(2000)039<0367:AONVWI>2.0.CO;2 |
| [28] | Xu M, Crook N A, Sun J, Assimilation of radar data for 1-4 hour snowband forecasting using a mesoscale model. Preprints, 14th Conf. On Numerical Weather Prediction, Fort Lunderdale, Florida, Amer. Meteor. Soc., 2001: 283–28. |
 2004, 15 (1): 95-110
2004, 15 (1): 95-110

