应用气象学报  2004, 15 (1): 10-20   PDF    
引用本文
李耀东, 高守亭, 刘健文. 对流能量计算及强对流天气落区预报技术研究[J]. 应用气象学报, 2004, 15(1): 10-20.
Li Yaodong, Gao Shouting, Liu Jianwen. A CALCULATION OF CONVECTIVE ENERGY AND THE METHOD OF SEVERE WEATHER FORECASTING[J]. Journal of Applied Meteorological Science, 2004, 15(1): 10-20  
对流能量计算及强对流天气落区预报技术研究
李耀东1,2, 高守亭1, 刘健文2     
1. 中国科学院大气物理研究所, 北京 100029;
2. 北京航空气象研究所, 北京 100085
2003-01-24 收到, 2003-05-22 收到修改稿.
资助项目: 本文受国家自然科学基金(No.40375016)和中国科学院知识创新工程(KZCX2-208)共同资助    
摘要: 文章分析了两种典型的大气湿绝热过程及其处理方法，对大气对流能量参数的计算技术进行了研究。结合实际个例，利用可逆饱和绝热过程，对包含液态水重力拖曳作用的修正对流有效位能(MCAPE)和修正下沉对流有效位能(MDCAPE)进行了定量计算。文章结合数值模式输出探空分析，预报不稳定和对流能量的区域分布，在此基础上建立了综合多指标叠套强对流天气落区预报方法，用MM5 及国家气象中心T106模式输出及诊断产品预报强对流天气落区，并检验强对流落区预报技术。
关键词: 可逆饱和绝热过程    修正对流有效位能(MCAPE)    修正的下沉对流有效位能(MDCAPE)    综合多指标叠套    强天气落区预报    
A CALCULATION OF CONVECTIVE ENERGY AND THE METHOD OF SEVERE WEATHER FORECASTING
Li Yaodong1,2, Gao Shouting1, Liu Jianwen2     
1. I nstitute of Atmospheric Physics , Chinese Academy of Sciences , Beijing 100029;
2. Beijing Aviation Meteorological Institute , Beijing 100085
Abstract: Two methods-pseudo equivalent potential temperature conservation and reversible moist adiabatic process are reviewed to deal with moist adiabatic process .Modified convective available potential energy (MCAPE) is int roduced to modify CAPE by presenting the gravitational effect of the condensed liquid water in upward convection .Modified downdraft convective available potential energy (MDCAPE) is defined to modify DCAPE by considering the dragging effect of liquid water .Real case studies show that liquid water plays more significant roles in rising parcel by diminishing CAPE largely than it does in downward f low by increasing DCAPE tenderly .Reversible moist adiabatic process is recommended in calculating MCAPE and MDCAPE .A synthetic multi-indicator superposition method is developed to predict the unstable and severe weather area based on the diagnosis of numerical model output .Experiment shows that the skill is practicable to both MM5 and Chinese National Meteorological Center T106 model output s.
Key words: Reversible moist adiabatic process     MCAPE     MDCAPE     Synthetic multi-indicator superposition     Severe weather forecasting    
引 言

强对流天气是最严重的自然天气灾害之一。虽然这种天气现象一直为各级气象部门所关注，并投入大量人力、物力，但至今仍缺少行之有效的预报手段。在我国，目前对这类天气的临近预报主要是根据实况(包括雷达和卫星)观测外推或根据预报员关于强天气的概念模式来进行。在国外(如美国)，利用加密的中尺度观测及卫星、雷达资料，采用变分同化技术，非静力中尺度模式对某些强对流天气的临近预报已显示出一定的能力[1]。而对于12 h 以上，目前的业务数值预报模式还不能真正预报强对流天气[2]。但强天气的发生也有规律可寻。现在的数值模式在短期形势预报方面已达到较高水平，美国原国家强风暴预报中心(NSSFC)下属的强风暴实验室(NSSL)自上世纪90年代初开始在实际业务中以数值预报资料为基础制作强对流天气的短期指导及展望预报[3]，90年代末，澳大利亚把决策树雷暴预报方法与数值天气预报模式结合起来[4]，使雷暴预报效率明显提高。而在我国，尚未见相类似的业务工作。最近几年，数值预报技术在国内有了长足的进步,各级气象业务部门已能得到大量高质量的数值预报产品，研究如何利用这些资料进行强对流天气的分析预报，把这种天气现象造成的损失降低到最低程度是十分必要的。

强对流天气的发生离不开深厚对流的发展，而深对流的发展必须具备三个条件，即不稳定存在、充分的水汽供应、一定的抬升条件，三者缺一不可[5]，其中，各种动力和热力不稳定的存在是对流发展的前提。大气特别是对于带有热力和质量强迫的强风暴系统[6],其不稳定问题非常复杂[7]，但位势和层结不稳定是强对流活动最重要的基本条件，而对流能量的大小又决定了对流发展的程度。因此，分析大气位势和层结不稳定、计算对流能量成为分析和预报强天气不可避免而且十分重要的问题。

强天气是一种深对流，而深对流又与湿对流紧密相关。用于表示大气稳定度的许多指数如沙氏指数[8]、抬升指数[9]等通常都与大气的湿绝热过程有联系，而大气对流能量的计算实质上就是求解大气湿绝热过程。本文将在回顾大气湿绝热过程处理方法的基础上，研究几个与强对流有关的能量参数及其计算方法，并采用可逆绝热过程计算包含水物质拖曳作用的对流能量参数。文章还将介绍综合多指标叠套预报强对流天气落区的思想方法，给出包含水物质拖曳作用的对流能量的计算实例，并给出强对流天气落区预报的统计检验及个例试验结果分析。

1 湿绝热过程处理及对流能量的计算与分析 1.1 湿绝热过程的计算分析

在预报对流性天气的发展时，传统的埃玛图(T-log p)分析是最常用的方法之一。埃玛图分析的关键在于计算状态过程，即干、湿绝热过程。其中，干绝热过程的计算比较简单。而对于湿绝热过程，目前主要有四种处理方法，即基于总温度守恒(湿静力能守恒)、假相当位温守恒、严格假绝热方程及可逆饱和绝热过程的处理思想。其中，假相当位温守恒和总温度守恒的物理实质是一样的，计算结果非常接近，这两种方法目前在我国最为常用；严格假绝热方程考虑了湿空气与干空气的比热贡献，计算较为复杂；可逆湿绝热过程考虑了气块中水物质及水汽两者的比热贡献。由于各种湿绝热过程内容和计算上都存在差异，针对不同的对流能量参数，有必要选用最适合的湿绝热处理方法。下面简单介绍一下假相当位温守恒和可逆湿绝热过程两种最典型的湿绝热过程的基本思想和计算方法。

1.1.1 假相当位温守恒

饱和气块绝热膨胀上升冷却凝结出的液态水可能会离开气块。假设液态水全部脱离气块，潜热保留在气块中，这就是所谓的假绝热过程。目前，世界气象组织(WMO)承认的假绝热方程为[10]:

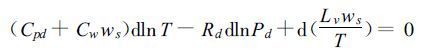
(1)

上式中，Cpd是干空气定压比热，Rd 为干空气的气体常数，Cw 为水汽比热，ws 为饱和水汽混合比，T为绝对温度，Pd 为干空气气压分量。一般情况下，ws 较小，在Cpd +Cwws≈Cpd的假定下，可导出假绝热过程中的守恒量假相当位温的表达式:

(2)
1.1.2 可逆饱和绝热过程

如果在湿绝热过程中，凝结出的水物质全部保留在气块中，其物理特性(温度和相态)随饱和气块而变化，并且考虑水汽与干空气的比热差异，则这种过程是可逆的，也是完全绝热的，被称之为可逆饱和绝热过程。对于含一定量水物质的饱和空气系统，其与假相当位温相对应的可逆饱和绝热过程的守恒量的表达式为:

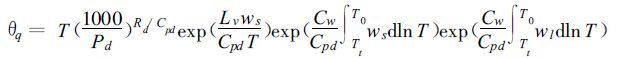
(3)

式中的wl 为液态水物质比含量，其它为气象惯用符号。其中，上式最后两项括号中的指数都是接近零的数，对数温度积分上下限为湿绝热起点T0 至大气顶Tt(z →∞，Tt →0)

式(3)的计算非常困难，而与式(3)相对应的可逆饱和绝热过程的微分形式为:

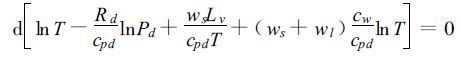
(4)

若定义:

(5)

则在可逆饱和绝热过程中，M即系统的熵是一守恒量，其计算要比θq简单得多。

以上两种方法实质上代表两种湿绝热过程，在具体求解时，可利用二分法[11]或迭代法求解假相当位温守恒方程(2)和可逆饱和绝热方程(5)。

1.2 大气对流能量参数及其计算 1.2.1 对流有效位能CAPE(E)与修正的对流有效位能MCAPE(E M)

CAPE 表示在自由对流高度之上，气块因正浮力作功而获得的能量。其具体表达式为:

(6)

式中，Zf 为自由对流高度，Ze 为平衡高度，Tva为气块虚温，Tve为环境虚温，Tve为自由对流高度和平衡高度之间环境的平均虚温。

实际计算时，常把上式转化到气压坐标系并按气压等间隔离散。这样，E的计算式变为:

(7)

上式求和区间为自由对流高度与平衡高度之间。

计算CAPE 的过程实质上就是求解湿绝热过程，若忽略虚温的影响，CAPE 即为通常埃玛图上正面积所对应的能量。事实上,CAPE 比传统意义上的对流不稳定能量更能恰当地表示出对流发展的强度，它作为对流发展的重要标志已经被直接或间接地投入业务使用[12]。

考虑了一定水物质含量wL 的重力拖曳后的正浮力能称为修正的对流有效位能(MCAPE)[13](用EM 表示)，其表达式为:

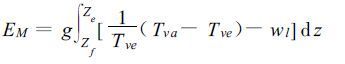
(8)

MCAPE 的概念提出后，一直缺少定量的计算。对上式粗略估计可看出，4 g·kg-1的液态水含量约可抵消气块与环境间1 ℃正温差所产生的浮力，由此可看出液态水的这种拖曳修正不是个小量。

由于液态水的含量难以确定，准确计算MCAPE 比较困难。本文在计算时，假定饱和凝结或冻结产生的水物质全部保留在气块中。若水物质保留在气块中，则其不可避免地与气块有显热交换，这样，用可逆饱和绝热过程替代假绝热过程来计算MCAPE 应更为合理。

1.2.2 下沉对流有效位能DCAPE(ED)与修正的下沉对流有效位能MDCAPE(EMD)

下沉运动是极常见的大气现象，对流下沉开始的最基本原因是干冷空气侵入含液态水的云体后，由于液态水蒸发而使气块降温，增大了局部层结温度递减率，从而使得下沉发生。假设气块沿假绝热线下沉至大气底，这条假绝热线与大气层结曲线所围成面积代表的能量称为下沉对流有效位能(DCAPE)[14]。其数学表达式为:

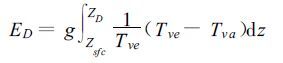
(9)

其中，ZD 和Zsfc分别表示起始下沉高度及地面高度。

下沉对流有效位能从理论上反映出下沉发生后，气块下沉到达地面时所具有的最大动能即环境对气块的负浮力能。计算DCAPE 时，首先必须确定下沉起始高度及下沉起始时的气块温度。一般把中层干冷空气的侵入点作为下沉起点，而一般又以大气在下沉起点的温度经等焓蒸发至饱和时所具有的温度作为气块开始下沉的温度。利用实际探空判断下沉起点时，可把中层大气中湿球位温或假相当位温最小的点对应的高度视为下沉起始高度，把该高度处的湿球温度作为下沉起始温度。

在分析对流下沉时，若假定含一定量液态水的气块按沿可逆饱和绝热线下沉，则可引入DCAPE 修正后的表达式MDCAPE(EMD):

(10)

注意，由于考虑了水物质的作用，必要时应采用可逆饱和湿绝热过程计算EMD。

2 对流能量参数计算及强天气落区预报试验 2.1 对流能量参数计算实例 2.1.1 北京1998年8月3日雷暴大风对流能量计算

图 1为根据1998年8月3日20:00(北京时，下同)北京站实况探空制作的探空分析图。与本个例对应，当晚22:00前后，北京市区发生了雷暴大风天气。

图 1. 1998年8月3日20:00北京站探空分析图

以地面P =1000.0 hPa，t =26.8 ℃，td =21.2 ℃ 作为抬升起点，则抬升凝结高度为919.9 hPa。如果按假相当位温守恒制作湿绝热线，自由对流高度为654.0 hPa，平衡高度为279.2 hPa ,CAPE 为263.6 J·kg-1。

在分析该个例假相当位温垂直结构时发现，θse897 -θse557 =23.5 K，而且在P =557.0hPa 处,θse最小，有相对干冷空气存在，根据DCAPE 的定义，可把该点P =557.0 hPa，t =-3.5 ℃，td =-6.3 ℃ 作为下沉开始的初始条件。气块在该处等焓蒸发至饱和时的温度即湿球温度为-4.8 ℃，假设此时的液态水含量为10.0 g·kg-1，以该状态作为可逆饱和湿绝热下沉起点，气块下沉至地面时温度为18.9 ℃，DCAPE 为1044.0 J·kg-1。在按可逆饱和湿绝热线下沉过程中，液态水逐渐蒸发以维持气块饱和，到达1000.0 hPa 时气块中的液态水仅剩余1.0 g·kg-1。下沉过程中，液态水的拖曳累计做功为268.9 J·kg-1 ,这样，修正后的DCAPE 即MDCAPE 为1312.9 J·kg-1。不计下边界刚性条件及液态水拖曳，理论上气块下沉到达地面的速度为45.7 m·s-1。若计液态水拖曳，下沉速度为51.2 m·s-1。

对本个例更深入的分析可发现，若对流有效位能真如以上所计算的那么小，则对流不可能发展很强盛，所计算的下沉对流也可能不会发生。事实上，目前国际上计算CAPE时，通常以近地面100 hPa 气层平均温湿特性或以近地面300 hPa 最不稳定的特性点作为抬升起点[15]。对本个例的假相当位温垂直结构分析可发现在897.0 hPa 存在这样最不稳定的特性点。图 2为以此处P =897.0 hPa，t =23.8 ℃，td =19.5 ℃ 作为抬升起点制作的探空图，图中湿绝热线为可逆饱和绝热过程线。在该情况下，抬升凝结高度为842.0 hPa，自由对流高度为730.3 hPa，平衡高度为170.7 hPa ,CAPE 为2250.1 J·kg-1 ,从自由对流高度至平衡高度，水物质拖曳所消耗的能量为1165.8 J·kg-1，MCAPE 为1084.3 J·kg-1。理论上，根据MCAPE 计算结果，气块在平衡高度处的垂直上升速度可达46.6 m·s-1。若以假相当位温守恒计算湿绝热过程，则CAPE 为1881.7 J·kg-1 ,MCAPE 为767.4 J·kg-1，可见不同的湿绝热过程对CAPE 和MCAPE 的计算有明显的影响。

图 2. 同图 1，抬升起点为897.0 hPa

该个例中，以假相当位温守恒计算出的DCAPE 与可逆饱和绝热线计算结果相近，这说明绝热过程的选择对DCAPE 的计算影响不大。

2.1.2 北京2000年7月3日局地强降水雷暴对流能量计算

图 3为2000年7月3日08:00北京站的探空分析图，图 4为其对应的湿球位温垂直结构。对应于本个例，当天下午15:00左右，北京发生了大范围雷暴大风和局地性强降水对流性天气。

图 3. 2000年7月3日08:00北京站探空分析图

图 4. 2000年7月3日08:00北京站湿球位温垂直结构

从图 4中可看出，在本个例中，最低层P =1004.0 hPa，t =26.4 ℃，td =23.5 ℃为条件不稳定，可视为抬升起点。若以假相当位温守恒计算湿绝热过程，则抬升凝结高度为962.3 hPa，自由对流高度为808.4 hPa，平衡高度为181.7 hPa ,CAPE 为2178.4 J·kg-1。从自由高度至平衡高度，凝结出的水物质拖曳所消耗的能量为1381.2 J·kg-1 ,MCAPE 为797.2 J·kg-1。若以可逆绝热过程来计算，则平衡高度为169.6 hPa ,CAPE 为2353.1J·kg-1 ,MCAPE 为842.3 J·kg-1。

从图 4中还可发现，中层特性点P =675.0 hPa，t =7.6 ℃，td =-4.4 ℃与地面之间的湿球位温差Δθsw =26.4 K，符合雷暴大风的定性预报条件[16]，可把该高度视为下沉起点。同样，假设在该处初始液态水含量为10.0 g·kg-1，该处对应的湿球温度为1.8 ℃。若气块沿假相当位温线下沉至1000 hPa，气块温度为18.0 ℃，气块中剩余的液态水含量为3.8 g·kg-1，在下沉过程中水的重力拖曳做功为225.3 J · kg-1，DCAPE 为768.0 J·kg-1，MDCAPE 为993.3 J·kg-1。若以可逆绝热过程计算下沉过程，则DCAPE为807.5 J·kg-1，MDCAPE 为1035.8 J·kg-1。

从对以上两个强对流活动的探空分析中的能量计算结果可以看出，在强的对流活动中，水物质拖曳所产生的消耗对上升对流活动的抑制是个相当大的量，不可以忽略；而水物质的拖曳对下沉对流有一定的促进作用。采用可逆饱和绝热过程计算的CAPE 要比采用假相当位温守恒方法的明显偏大，而对DCAPE 而言，两种湿绝热过程的计算结果差异不大。

2.2 强天气落区综合多指标叠套预报方法试验

强对流天气发生在对流活跃区域，对流发生的基本条件为条件不稳定层结的存在、充分的水汽供应和一定的启动机制。从不同尺度系统的相互作用来考虑，大尺度系统对中小尺度系统的发生起着控制作用，因而我们可以综合各种大尺度条件来预报对流天气的发生。

本文分别以国家气象中心T106模式1995～1997年的预报场和区域MM5模式输出产品为基础，进行了综合多指标叠套强天气预报试验。综合多指标叠套包括了以下过程:常规物理量产品诊断、强对流因子计算、条件不稳定判断、强天气消空、综合多指标叠套强天气落区预报。所选取的叠套指标分别为低层温度露点差、K 指数、稳定度(低层垂直假相对位温倾向)、低层水汽通量散度、中低层垂直速度、低层散度、中低层涡度、对流有效位能、沙氏指数、垂直风切变。

2.2.1 基于T106资料的强天气落区预报试验

试验以国家气象中心T106模式1995～1997年(1°×1°)的预报分析场为基础，对这3年夏季分别进行了综合多指标叠套强天气落区预报，以全国435个站24 h 强天气实况对预报情况进行了独立样本检验。以1997年夏季为例，强天气预报临界成功指数CSI =0.191，击中率POD =0.628，预报效率EH =0.859，1995 、1996年预报水平都略低于1997年。有一点值得说明，这里的强天气标准以地面观测与雷暴、冰雹、飑线等17种标准天气现象记录为准，比严格的强对流天气标准[17]略偏松。

图 5为1997年8月31日20:00预报9月1日20:00强天气落区与实况强对流天气分布图。可以看出，9月1日20:00，全国435个地面站中有强对流天气记录的有35个站。8月31日20:00对该时次的24 h 综合多指标叠套预报情况为，报对强对流天气的有26个站，漏报9个站，空报54个站，预报无强对流，实况未出现强对流的有346个站。对本个例而言，强对流预报的击中率POD =0.743，CSI =0.292，EH =0.855。从宏观上看，预报强天气落区与实况强天气落区比较一致。

图 5. 1997年8月31日20:00 24 h 强天气预报落区与9月1日20:00强天气发生实况图
(综合多指标叠套预报有强天气的格点以圆圈标识，站点发生强天气以黑点标识，没有强天气的站点以浅色点标识位置)

2.2.2 MM5模式强天气落区预报试验

为检验本文的预报方法，采用MM5中尺度数值模式24 h 预报结果，进行了强天气落区业务预报试验，试验时段为2000年5月1～31日。模式预报的范围为55 ×51，中心点为(117°E，35°N)，水平格距60 km，垂直分为21层。初始资料为每天20:00地面和高空探空报文的客观分析场。同时，试验时还计算了一些其它强对流如强天气威胁指数[18]的区域分布。

预报区域内有观测记录参与检验的总站次为8657，24 h 强天气预报结果是:实际发生强天气(即20:00实况天气记录为强天气)169站次，预报正确89次，空报459站次，漏报80站次。强天气预报临界成功指数CSI =0.142，击中率POD =0.527，预报效率EH=0.938。这一预报结果略差于T106的强天气预报结果，其主要原因之一可能是5月份强天气发生概率偏低。

试验期间无大范围系统性强对流天气，只有两次范围不大的较为系统性的强对流天气。下面就其中的一次过程进行预报效果分析。

2000年5月6至7日，500 hPa 一支南北向小槽移过河套地区，在地面锋前造成了较为系统性强对流天气过程。图 6为5月6日24 h 对流有效位能区域预报，图 7为24 h 强天气威胁指数区域预报，图 8为24 h 强天气落区区域预报，图 9为5月7日20:00实况强天气分布图。从区域分布图来看，强天气落区预报的形状和位置较为准确，但在河套北部空报区较大。从图 6和图 7还可看出，对流有效位能和强天气威胁指数对强天气落区有一定的指示性。

图 6. 2000年5月6日20:00 24 h 对流有效位能预报图

图 7. 2000年5月6日20:00 24 h 强天气威胁指数预报图

图 8. 2000年5月6日20:00 24 h雷暴落区预报

图 9. 2000年5月7日20:00实际强对流天气落区
(图中“ ○” 点为强对流天气发生地点)

3 结论与讨论

强对流天气的分析和预报与大气不稳定度和对流能量计算密切相关，而不稳定和对流能量的计算不可避免要涉及计算湿绝热过程。本文介绍了两种大气湿绝热过程的处理方法，其中，假绝热过程假设所有凝结出的水物质全部脱离气块，而可逆绝热过程则假设所有凝结出的水物质都保留在气块中，两种方法趋向两个极端。可逆湿绝热过程不仅考虑了水汽与干空气的比热差异，而且考虑了所凝结出的水物质的感热贡献，因此用这种绝热过程来计算含液态水的大气热力过程理论上相对比较合理。

对流有效位能CAPE 和下沉对流有效位能DCAPE 从理论上反映了对流上升和下沉运动可能发展的程度，若计入液态水的拖曳，则分别可用MCAPE 和MDCAPE 来修正。对于发展强盛的深对流，上升运动中水物质的拖曳并不是个小量，这解释了为什么通常根据气块理论计算所得到的CAPE 往往比实际大气中发生的对流强度大得较多的原因之一。

液态水含量是一棘手的问题。本文在计算MCAPE 和MDCAPE 时，假设凝结出的液态水完全不脱离气块，夸大了液态水的拖曳作用，这种假设与实际大气过程也存在差距。为了与CAPE 对比，本文在计算MCAPE 时没有考虑因水物质重力拖曳而使得自由对流高度升高，平衡高度降低这种力学效应对MCAPE 计算可能造成的影响，而采用与CAPE相同的自由对流及平衡高度。若在计算这些物理过程时代以更为实际的水物质观测值,再部分考虑气块的夹卷效应，计算出的大气湿绝热过程和大气对流能量与实际应更为接近。

对流能量参数与对流发生的强度关系紧密，对强天气的预报有指示意义。强天气发生有一定规律，必须具备一些基本的大尺度条件，这些基本条件是否满足可以通过对数值预报模式产品的进一步诊断来判别。综合多指标叠套技术基于这种思想，其实质相当于一种集成预报方法。若采用的各种指标较全面地反映强天气的特征，利用这种方法来预报强对流天气落区理论上是可行的。在这种思想的指导下，本文进行了初步的尝试和试验，但要更准确地预报强天气落区，针对不同模式、不同区域、不同季节，选用的叠套参数及指标都有很多值得探讨和改进的地方。另外，多指标叠套归类于完全预报技术，预报的成功与否还取决于模式的预报性能。

致谢 本文内容为北京航空气象研究所“ 区域强对流天气数值分析预报系统”课题研究的一部分，在此，感谢课题组各成员对本文工作所提供过的支持。此外，感谢中国气象局预报逐级指导技术子课题“冰雹落区预报逐级指导技术研究”提供的相关技术和文献。
参考文献
[1] Wu Bing, Dynamical and microphysical retrievals from Doppler radar observations of a deep convective cloud. J Atmos Sci., 2000, 57: 262–283. DOI:10.1175/1520-0469(2000)057<0262:DAMRFD>2.0.CO;2
[2] 国外强对流天气的应用研究, 北京: 气象出版社, 2001: 3-17.
[3] Obsty F P, Operations of National Severe Storms Forecast Center. Wea Forecasting, 1992, 17: 546–562.
[4] Mills G A, Colquhoun J R, Objective prediction of severe thunderstorm environments: Preliminary results linking a decision tree with an operational regional NWP model. Wea Forecasting, 1998, 13: 1078–1092. DOI:10.1175/1520-0434(1998)013<1078:OPOSTE>2.0.CO;2
[5] Sherwood S C, On moist instability. Mon Wea Rev., 2000, 128: 4139–4142. DOI:10.1175/1520-0493(2000)129<4139:OMI>2.0.CO;2
[6] Gao Shouting, Lei Ting, Zhou Yushu, Moist potential vorticity anomaly with heat and mass forcings in torrential rain systems. Chin Phys Lett., 2002, 19: 878–880. DOI:10.1088/0256-307X/19/6/340
[7] Schultz D M, Schumacher P N, Doswell C A, The intricacies of instabilities. Mon Wea Rev., 2000, 128: 4143–4148. DOI:10.1175/1520-0493(2000)129<4143:TIOI>2.0.CO;2
[8] Showalter A K, A stability index for thunderstorm forecasting. Bull Amer Meteor Soc., 1953, 34: 250–252.
[9] Galway J G, The lifted index as a predictor of latent instability. Bull Amer Meteor Soc., 1956, 37: 528–529.
[10] Bolton D, The computation of equivalent potential temperature. Mon Wea Rev., 1980, 108: 1046–1953. DOI:10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2
[11] 李耀东, 刘健文, 刘玉玲, 等. 埃玛图微机制作及对流有效位能的计算. 气象, 1998, 23, (5): 21–25.
[12] Huntrieser H, A New Thunderstorm Index for Switzerland.18th Conference on Severe Local Storms. Amer Meteor Soc, 1996: 255–259.
[13] 吴宝俊. 对流天气分析预报中引入的几个新参数. 航空气象科技, 1998, 2: 8–10.
[14] Emanuel K A. Atmospheric Convection. Oxford University Press, New York, 1994.
[15] Rochette S M, The importance of parcel choice in elevated CAPE computations. National Weather Digest., 1999, 23: 20–32.
[16] 中尺度天气原理和预报, 北京: 气象出版社, 2000: 268-273.
[17] Johns R H, C A Doswell Ⅲ, Severe local storms forecasting. Wea Forecasting, 1992, 7: 588–612. DOI:10.1175/1520-0434(1992)007<0588:SLSF>2.0.CO;2
[18] Miller R C, Maddox R A, Use of the SWEAT and SPOT indexes in operational severe storm forecasting. 9th Conference on Severe Local Storms. Amer Meteor Soc., 1975: 1–6.