2. 中国气象科学研究院, 北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing, 100081
蒸散过程是土壤-作物-大气连续体内水分循环的重要环节,农田蒸散量的计算是实施节水计划,进行合理灌溉的重要科学依据之一,而蒸散模式是计算农田蒸散量的核心。目前世界上较为常用蒸散模型分为参考蒸散和实际蒸散两类:参考蒸散模式中较为常用的是Penman模式和Priest ley-Taylor模式; 实际蒸散模式中常用的是密集植被状况下的Penman-Menteith单源模型和稀疏植被状况下的Shut tlew orth-Wallace双源模式。相对而言,实际蒸散模型涉及的物理过程和参数较多,理论推导严密,在计算农田实际蒸散时误差较小; 但因涉及的参数繁多,在实际观测中难于获取。不少学者对上述蒸散模式进行了对比研究,如Stannard (1993)[1]在半干旱牧场的自然植被状态下对Penman-Menteith模式、Shut tlew orth-Wallace模式和Priestley-Taylor模式进行了对比,结果表明:在稀疏植被状况下Priestley-Taylor模式与Shut tlew orth-Wallace模式的结果相近,优于Penman-Menteith模式; Kustas等 (1996)[2]对Penman-Menteith模式和Priestley-Taylor模式的参数进行了对比试验,发现在一些地区Priestley-Taylor模式与实际情况更为接近。还有许多学者对Priestley-Tay lor模式进行了应用和验证,Stew art等 (1977)[3]利用Priestley-Tay-lor模式计算了较高纬度地区湿润表面的蒸散; 利用Priest ley-Taylor模式中山敬一等 (1982)[4]计算了不同作物的蒸散,刘邵明 (1998)[5]计算了新疆棉田的潜在蒸散; 王西平等 (1998)[6]将Priestley-Taylor模式作为蒸散的基本模式用于VSMB多层次土壤水分平衡动态模式对我国华北地区的冬小麦土壤墒情进行模拟,均取得了令人满意的结果。他们的研究结果表明参数较少的蒸散模式可用于农田蒸散计算。另一方面,世界粮农组织 (FAO) 在简化蒸散模式方面也作了大量研究,1979年曾以Penman模式为基础,建立了参考蒸散模式; 1998年又对Penman-Mentei th模式进行了简化,研制出了新的参考蒸散模式,为计算区域性作物蒸散奠定了基础。
玉米为高杆稀植作物,生长季高温、多雨,其蒸散和水分消耗过程较其它作物更为复杂。许多学者对玉米冠层的潜热交换系数及阻力进行了研究,我国学者利用Penman和Penman-Menteith模式对玉米的蒸散进行研究,在玉米蒸散计算方面取得了一些进展,但采用简化模式针对业务服务应用的研究尚不多见。本文通过田间试验和资料统计方法,着重对以辐射和常规气象要素为参数的Priest ley-Taylor模式和FAO推荐的Penman-Menteith模式改良的作物参考蒸散模式进行对比,探讨利用简化模式计算玉米田蒸散的可能性,建立不同土深玉米田作物系数方程,用以计算玉米田实际蒸散。
1 试验方法试验在河北省定兴县中国气象科学研究院农业气象试验基地 (39°08′N,115°48′E,海拔高度为25 m) 进行。试验期为1999年7月1日至9月30日,共92天。试验地种植作物为玉米,种植密度为68000株/hm2。玉米播种期为6月18日,成熟期为10月5日,全生育期109天,玉米叶面积和高度等生物量调查每10天进行一次。试验在无灌溉条件下进行,气象观测场距试验地20m,试验期间总降水量212.2 mm,为干旱年型。土壤水分每5~6天测定一次,在大田中分9个小区,每个小区设1个点取样,计算中采用9个小区平均土壤湿度。0~30 cm土壤水分观测采用烘干法,40~300 cm土壤水分观测采用中子仪法。
在资料分析中采用了1991~1995年黄骅 (38°22′N,117°21′E,海拔高度6.6 m)、德州 (37°26′N,116°19′E,海拔高度22.7 m)、新乡 (35°19′N,113°53′E,海拔高度74.0 m)、卢氏 (34°03′N,111°02′E,海拔高度569.9 m)、南阳 (33°02′N,112°35′E,海拔高度130.7 m)5站的逐日气象要素和除德州外4站0~50 cm土壤湿度观测资料。
2 蒸散模式 2.1 Priestley-Taylor模式自Penman (1948) 蒸发方程建立以来,各国学者在此基础上建立了许多模式计算蒸散量,作为水分充足条件下大气环境对蒸散影响的参照标准,其中“平衡蒸发理论”多年来在试验研究中广为使用。这一理论定义为在水分充足的情况下,蒸发速率受制于蒸发表面所接收到的太阳辐射、风速和饱和差,即:
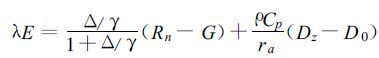
|
(1) |
式中λE为蒸发潜热 (MJ°m-2°d-1); Δ为饱和水汽压-温度曲线斜率 (hPa°K-1),γ为干湿表常数; Rn为净辐射 (MJ°m-2°d-1); G为土壤热通量 (MJ°m-2°d-1); ρ为空气密度 (kg°m-3); Cp为空气定压比热 (MJ°kg-1°K-1); Dz为参照高度的空气湿度 (hPa),D0为蒸发表面的空气湿度 (hPa)。
在表面湿润状况下,即D0=Dz,表面蒸发可表示为 (Slatyer和Mcilroy,1961)[7]:
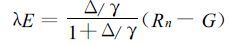
|
(2) |
在式 (2) 基础上,Priest ley和Taylor (1972)[8]对包括水体和作物面在内的不同下垫面的蒸散进行了试验,认为在无平流和水分条件不受抑制的情况下,潜热交换以一定的速率进行,得出潜热交换的平均参数 (α),并以此建立了适用于大尺度湿润表面的蒸散模式:
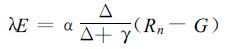
|
(3) |
式中α为常数 (=1.26)。
2.2 FAO (1998) 作物参考蒸散模式Menteith在平衡蒸发的理论基础上,把植被看成一个整体,假定作物冠层为一片大叶,潜热交换发生在叶面上,得出计算植被状况下实际蒸散的组合方程:
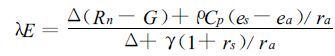
|
(4) |
式中rs和ra分别为表面阻力和空气动力阻力,由于该模式涉及的参数较多,其中部分参数在常规观测中无法获取,使模式的使用受到一定的限制。FAO (1998) 对Penman-Menteith模式中的阻力参数进行了简化[9],以充分湿润、高度为12 cm、单叶气孔阻力为100 s°m-1的草地为参照表面,计算参考蒸散,将式 (4) 改写为:
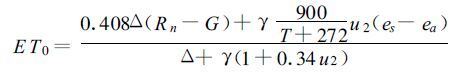
|
(5) |
式中ET0为参考蒸散量 (mm°d-1),T为2m高的平均气温 (℃),u2为2m处风速 (m°s-1),es为饱和水汽压 (kPa),ea为实际水汽压 (kPa),其余各项均与式 (3) 相同。
模式中净辐射 (Rn) 均采用下式[9]计算:
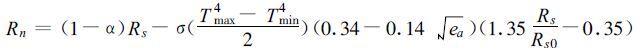
|
(6) |
式中α为玉米地反射率 (0.15)[10],Rs为太阳辐射 (MJ°m-2°d-2),σ为斯蒂芬-波尔兹曼常数 (=4.903 ×10-9 MJ°K-4°m-2°d-1),Tmax为最高温度 (K),Tmin为最低温度 (K),ea为实际水汽压 (kPa),R s0为晴空太阳辐射 (MJ°m-2°d-2)。
太阳辐射 (Rs) 由下式计算:
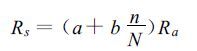
|
(7) |
式中a,b为系数 (分别为0.25和0.50),n为日照时数 (h),N为可照时数 (h),Ra为大气外辐射 (MJ°m-2°d-2)。
晴空太阳辐射 (Rs0) 由下式计算:
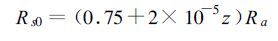
|
(8) |
式中z为海拔高度 (m)。
2m高度的风速 (u2) 由下式计算[9]
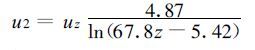
|
(9) |
其中uz为z高度的风速 (m°s-1)。
由于模式中涉及的土壤中热流量很小[4,9],在计算蒸散量时被忽略。
3 结果 3.1 参考蒸散计算结果Priestley-Tay lor模式是建立在无平流的基础上的,在计算中利用文献[10]和[12]中的方法对α进行大气层结稳定度修正:
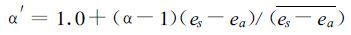
|
(10) |
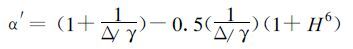
|
(11) |
式中α′为Priestley-Taylor模式修正后的α,(es-ea) 为长周期平均饱和差,H为空气相对湿度。
用试验地1999年6月至9月和华北5个站1991~1995年的逐日气象观测资料计算结果表明:在大多数情况下Priestley-Taylor模式计算的参考蒸散量大于FAO的Penman-Menteith模式计算的参考蒸散量,两者间存在着良好的线性关系。Priestley-Taylor模式中仅含有辐射项,而FAO的Penman-Mentei th模式则可分解成辐射项和动力项。对比两模式中辐射项的常数,可看出Priest ley-Taylor模式中的辐射项比FAO Penman-Menteith模式中的辐射项约大20 %左右,并且后者会随风速的增大而减小; FAO Penman-Menteith模式中的动力项与风速和饱和水汽压差成正比,与气温成反比。在晴朗、微风的天气条件下,Priestley-Taylor模式计算的参考蒸散大于FAO Penman-Mentei th模式的计算结果,在干燥多风的天气条件下则相反。从试验点和华北5个站2000多个计算值对比,大部分情况下两种模式的计算结果呈良好的线性关系,动力项造成的差异一般在30 %以下,但在华北东部的黄骅和德州站,由于风速较大,动力项造成的差异可高达70 %~80 %。但在建立实际蒸散计算方程时二者间的差异是否会造成大的误差还需要进一步讨论。
3.2 实际蒸散计算实际蒸散一般由参考蒸散与作物系数的积来表示,即:

|
(12) |
式中Ea为实际蒸散量,kc为作物系数,Erc为作物参考蒸散量。
作物系数是由作物表面和其空气动力特性等因素所决定的综合因子,Wallace (1995)[13]对多种作物系数进行了细致的对比研究,由Penman-Menteith方程导出作物系数 (kc) 的理论算式:
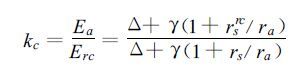
|
(13) |
式中rsrc (69 s°m-1) 为蒸散速率达到参考蒸散量时的作物表面阻力,ra为空气动力阻力 (s°m-1),rs为表面阻力 (s°m-1)。
由于阻力因素与环境条件之间的关系十分复杂,加之求取参考蒸散的方法不同,因此实际蒸散与理论值之间存在一定误差。在实际计算中,通常采用经验方法。Davies (1973)[14]利用土壤表面相对湿度与Priestley-Tay lor参考蒸散建立非湿润表面状态下的实际蒸散方程; 中山敬一等 (1993)[15]将Davies的研究进一步深化,应用于马铃薯等作物浅根层土壤水分预报,Lu等 (1997)[16]曾将这一研究结果用于干旱条件下的玉米田土壤水分预报; 刘邵明[5]用叶面积系数、土壤有效水分和Priest ley-Taylor参考蒸散建立了棉田实际蒸散的计算方法,都取得了较好的效果。
由于试验是在大田的自然状态下进行的,实际蒸散量是以水分平衡方程为基础计算出的土层实际水分消耗量。分别对土壤表层、浅根层、根层和较深土层 (0.1 m、0.5 m、1m、2m和3 m) 土壤水分的实际变化量进行了分析,考虑到土壤水分对作物根系吸水和表面阻力影响较大,以平均土壤相对湿度为因子,建立作物系数的经验方程[13]:
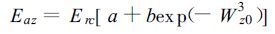
|
(14) |
式中Eaz为不同深度的实际水分消耗量 (mm),Erc为参考蒸散 (或潜在蒸散)(mm),a,b为经验常数,Wz0为z深度前一时段的平均土壤相对湿度。
在式 (12) 中采用Priestley-Taylor参考蒸散为作物参考蒸散计算50 cm深度的作物系数效果较好,其a,b值分别为1.640和-1.368,相关系数为0.550,达到0.05的显著水平。
考虑到除去土壤水分对蒸散的综合影响外,作物叶面积对蒸腾影响极大,又以叶面积系数和土层土壤相对湿度为因子,与Priestley-Tay lor参考蒸散和FAO作物参考蒸散建立了作物系数的经验方程 (式 (15)),计算玉米田不同土层的实际水分散失量。
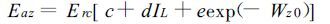
|
(15) |
c,d,e为经验常数,IL为叶面积系数。
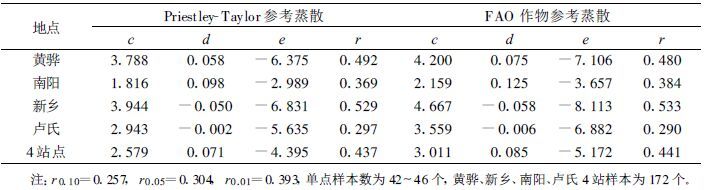
方程 (15) 中各土层的经验常数和相关系数 (r) 在表 1中列出。由表 1可以看出,除3 m土层外,两种模式建立的作物系数方程显著性较高。
|
|
表 1 采用Priestley-Taylor参考蒸散和FAO作物参考蒸散建立的作物系数方程 (15) 中的经验常数和相关系数 |
用黄骅、南阳、新乡、卢氏1991~1994年6月中旬至9月下旬0~50 cm土壤水分资料建立与上述方程相同形式实际蒸散方程,经验常数和相关系数在表 2中列出。
|
|
表 2 采用观测站资料和Priestley-Taylor参考蒸散和FAO作物参考蒸散建立的作物系数方程 (3) 中的经验常数和相关系数 |
将两种实际蒸散模式结果进行比较,二者差异较小; 并用南阳、新乡、卢氏3站1995年观测资料对本站的模式进行验证,平均相对误差10 %左右,在较强降水情况下误差较大; 相对而言,南阳和新乡的结果较好。1999年和2000年均为干旱年份,尤其是1999年夏玉米生长季内旱情十分严重,为考察模式在干旱年份的稳定性,采用了山西运城、河北霸县、唐山、河南新乡、卢氏、郑州、南阳、商丘8个站1999年至2000年夏玉米生长季的土壤湿度资料对利用4站资料建立的模式进行验证,平均相对误差一般为10 %~15 %左右,其中霸县、新乡、郑州、卢氏、南阳、商丘结果较好,而运城和唐山在1999年干旱情况下产生的误差达30 %以上。表明在强降水和干旱严重情况下模式缺乏稳定性,还需要进一步研究,加以修正。
4 结论用简化的蒸散模式计算农田实际蒸散可避免观测要素不足和多种假设参数的不便。利用参数较少的Priestley-Tay lor模式和FAO (1998) Penman-Menteith模式均可计算的参考蒸散,采用Priestley-Tay lor模式计算亦能取得较好的效果,为计算玉米田不同深度土壤水分消耗量,特别是较深土层水分消耗量提供了简便可靠的方法。但由于试验地点和资料的局限性,以及气候条件的特殊性,上述模式的实际蒸散计算,尤其是干旱条件下实际蒸散的计算的误差较大,还需进行进一步研究。
| [1] | Stannard D I, Comparison of Penman-Monteith, Shuttleworth-Wallace, and modified Priestley-Taylor evapotranspiration models for wildland vegetation in semiarid rangeland. Water Resour. Res, 1993, 29, (5): 1379–1392. DOI:10.1029/93WR00333 |
| [2] | Kustas W P, Stannard D I, Allwine K J, Variability in surface energy flux partitioning during Washita's 92 : Resulting effects on Penman-Monteith and Priestley-Taylor parameters. Agric. Forest. Meteor, 1996, 82: 171–193. DOI:10.1016/0168-1923(96)02334-9 |
| [3] | Stewart R B, Rouse W R, Substantiation of the Priestley and Taylor parameter=1.26 for potential evaporation in high latitudes. J. Appl. Meteor, 1977, 16: 649–650. DOI:10.1175/1520-0450(1977)016 & lt; 0649:SOTPAT & gt; 2.0.CO; 2 |
| [4] | 中山敬一, 中村彰宏. Priestley-Taylorモデルによる蒸発, 散位の推定. 农业气象, 1982, 37, (4): 297–302. |
| [5] | 刘邵明. 用Priestley-Taylor模式计算棉田实际蒸散量的研究. 应用气象学报, 1998, 9, (1): 88–92. |
| [6] | 王西平, 姚树然. VSMB多层次土壤水分平衡动态模式及其初步应用. 中国农业气象, 1998, 19, (6): 27–31. |
| [7] | Slatyer R O, McIlroy I C. Practical microclimatology. UNESCO (Paris). 1961. |
| [8] | Priestley C H B, Taylor R J, On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Wea. Rev, 1972, 100: 81–92. DOI:10.1175/1520-0493(1972)100 & lt; 0081:OTAOSH & gt; 2.3.CO; 2 |
| [9] | Allen R G, Perira L S, Raes D, et al. Crop evapotranspiration. FAO Irrigation and Drainage Paper 24, Rome. 1998. |
| [10] | Jury W A, Tanner C B, Advection modification of the Priestley and Taylor evapotranspiration formula. Agron. J, 1975, 67: 840–842. DOI:10.2134/agronj1975.00021962006700060031x |
| [11] | 张志明. 湿润下垫面的近地面层内感热和潜热垂直通量的计算. 成都科技大学学报, 1984, 2: 89–96. |
| [12] | 傅抱璞, 翁笃鸣, 虞静明, 等. 小气候学. 北京: 气象出版社, 1994: 349. |
| [13] | Wallace J S, Calculating evaporation:resistance to factors. Forest Meteor, 1995, 73: 353–366. DOI:10.1016/0168-1923(94)05084-J |
| [14] | Davies J A, Allen C D, Equilibrium, potential and actual evaporation from cropped surfaces in southern Ontario. J. Appl. Meteor, 1973, 12: 649–657. DOI:10.1175/1520-0450(1973)012 & lt; 0649:EPAAEF & gt; 2.0.CO; 2 |
| [15] | Nakayama K, Kon H, Matsuoka N, Estimation of soil moisture in the shallow root zone region. J. Agric. Meteor, 1993, 48, (5): 851–854. DOI:10.2480/agrmet.48.851 |
| [16] | Lu H Q, Nakayama K, Yu G R, Application of revised Priestley-Taylor model for soil moisture prediction in a maize field under drought condition. J. Agric. Meteor, 1997, 52, (5): 473–476. DOI:10.2480/agrmet.52.473 |
 2003, 14 (6): 722-728
2003, 14 (6): 722-728