气象要素空间插值方法在数值天气预报客观分析研究已久,目前已发展为使用不同来源观测资料的四维变分同化方法。农业气候资源研究中根据气象要素形成的气候学成因建立其与经度、纬度和海拔高度及其它地理因子影响的回归方程,进而推算得到空间格点月、季、年值气象要素场[1,2]。近几年来,克立格法 (Kriging) 等地统计学方法在气象单要素以及土壤观测资料等空间插值中得到较多应用[3-5],对历史气象要素插值的时间尺度也发展到月、旬[6、7]。
当前面向作物生长过程,主要以气候为驱动变量的作物模拟模型正在由单点或田块尺度向区域尺度应用方面发展,并开始在气候变化影响评估等方面得到应用。为了在区域尺度运行以逐日气象要素为输入因子的作物生长模型得到区域分布结果,需要对逐日气象要素输入变量进行空间插值。鉴于日气象要素场的时空变异较大,选择适当的空间插值方法进行格点化以适应作物生长模拟的需求,成为作物模型区域化应用的关键。本文选择距离权重反比法 (IDW)、梯度距离权重反比法 (GIDW) 以及地统计学中的克立格法 (Kriging)3种方法进行比较分析,以得到最佳的结果。
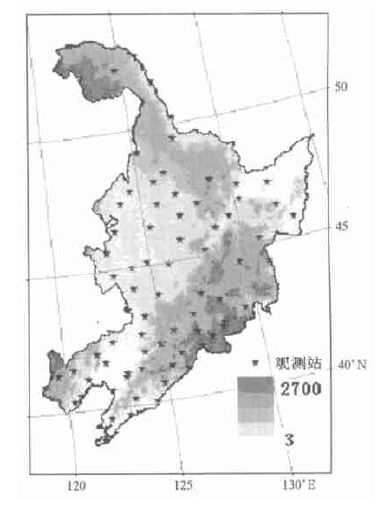
1 资料与处理 1.1 资料来源在尽可能使用更多实测资料的原则下,选择东北地区具有连续完整的1961~2000年逐日最高温度、最低温度和降水量的72个气象观测站。除黑龙江北部较稀外,其余观测站分布较为均匀,如图 1所示。
|
|
| 图 1. 东北地区观测站分布 | |
通过空间插值方法计算,把逐日最高温度、最低温度和降水量插值到38.5°~54°N,118.5°~135.5°E范围内0.25°×0.25°的网格点上。除东北地区边界以外的点,共生成1455个网格点。
对逐日最高温度和最低温度进行海拔高度影响订正采用1:25万 (100m×100m) 的DEM高程模型。
1.2 空间插值方法 1.2.1 距离权重反比法 (IDW)距离权重反比法 (Inverse Distance Weighting,简称IDW) 是一种常用而简便的空间插值方法,它以插值点与样本点间的距离为权重进行加权平均,离插值点越近的样本点赋予的权重越大。若权重用距离反比,称为距离反比法; 权重用距离平方反比时称为距离平方反比法。在实际应用中,通常选择后者。表达式如下:
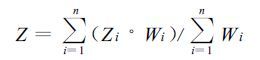
|
(1) |
式中,n为用于插值的气象观测站点的数目,Z为估计的格点的气象要素值,Zi为气象要素在第i个站点的实测值,Wi为第i个站点的权重系数。
对于权重系数Wi,通常的简便计算方法是以格点到观测点的大圆半径的平方反比作为权重系数[7],而不考虑观测点要素在方向如经向、纬向的不同变化。本研究认为,作为气象要素本身所具有的地理属性特征,日最高温度、最低温度和降水量随经向和纬向有不同的变化。因此,本文根据数据点的分布方向确定权重系数Wi[8],即由搜索圆半径决定在不同的方向上取3~10个点,分别计算经向和纬向方向的权重系数Wi,x、Wi,y,再计算出数据点的权重,其计算公式如下:
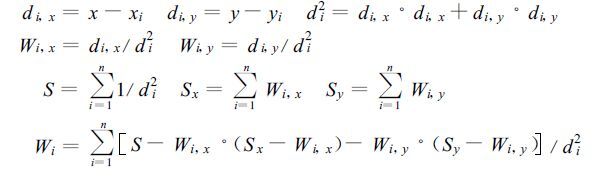
|
(2) |
式中,x、y、x i、yi分别为格点和站点用经纬方式进行地球投影的平面直角坐标,d为距离。
1.2.2 梯度距离权重反比法 (GIDW)梯度距离权重反比法 (Gradient plus Inverse Distance Weighting,简称GIDW) 是对距离权重反比法的扩充,即在距离权重的基础上,进一步考虑了气象要素随海拔高度的变化,如下式中的第二部分:
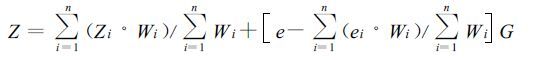
|
(3) |
式中,Z为待估格点的气象要素值,Zi为气象要素在第i个站点的实测值,e和ei分别为待估格点与气象观测站点的海拔高度,G为气象要素随海拔高度变化的梯度。
1.2.3 克立格法 (Kriging)克立格法近年来在地质、气象等研究领域里得到广泛应用。它的分析工具是半变异函数 (Semivariogram),对空间分布具有随机性与结构的变量的研究具有独特的优点[7]。
对任一空间变量点处的估计值Zx*,可以通过对该点影响范围内的n个有效观测值Z(Xi) 的线性组合得到,即

|
(4) |
式中,λi是赋予气象观测值Z(X i) 的权重系数,表示各站点气象要素值Z(X i) 对估计值Zx*的贡献。为达到线性无偏估计,使估计方差最小,权重系数由普通或简单克立格 (Ordinary/Simple Kriging) 方程组求得。同时,权重系数取决于变量的空间结构性,而任何变量的空间结构由半变异函数γ(h) 表示:
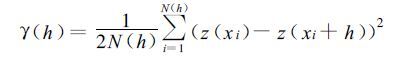
|
(5) |
式中,h为距离矢量,N(h) 为相距h的数据对的数目。本研究对不同半变异函数模型进行的试验、拟合和比较结果表明,对于日最高、最低温度的逐日插值采用幂函数模型 (Power)、空洞效应模型较为理想; 而对于日降水量的插值,可选择二次 (Quadratic) 或幂函数模型。
1.3 检验评估对于不同空间插值方法的估计值效果的检验,一般采用交叉验证法 (cross-validation) 来验证其插值的效果[4]。即分别假设每一站点的气象要素值未知,用周围站点的值来估算,然后根据所有站点实际观测值与估算值的误差大小评判插值方法的优劣。本文采用平均绝对误差 (MAE) 和均方根误差 (RMSE) 作为评估3种方法插值效果的标准。前者反映样本数据估值的总体误差或精度水平,后者反映利用样本数据的估值灵敏度和极值。
此外,为了检验插值后数据点的整体分布情况,还采用数理统计分析方法,计算插值数据点的最大值、最小值、平均值和标准差等统计量,以比较插值前后气象要素场总体分布特征。
2 气象要素的梯度及年内变化特征鉴于前面所述,本文进行气象要素空间插值时需要考虑经度和纬度不同方向上距离对插值数据点的影响,因此研究中首先分析了逐日气象要素随经度、纬度和海拔高度的变化梯度及其在年内的变动特征。计算了东北72个站点日最高温度、最低温度和降水量3个要素的40年平均值,分别与经度、纬度和海拔高度3个因素进行多元回归统计分析,分别得到年内每日最高温度、最低温度和降水量与经度、纬度和海拔高度的偏回归系数,用以表示气象要素随经度、纬度和海拔高度的变化梯度。最高、最低温度和降水量与3个要素的复相关系数较高,均通过显著性 (α=0.001) 统计检验,其中降水量的相关程度低于温度。
2.1 经向梯度及年内变化特征从图 2(a)可以看出,逐日最高、最低温度普遍随经度增大而下降,且年内有明显的起伏波动。最高温度经向梯度 (下降) 冬季最明显,稳定在0.3~0.5 ℃/经度之间; 4~5月和7~11月较小,约0~0.2 ℃/经度。最低温度经向梯度年内变化不如最高温度明显,秋末、冬季至春季为0~0.3 ℃/经度左右,盛夏至初秋7~10月更小。
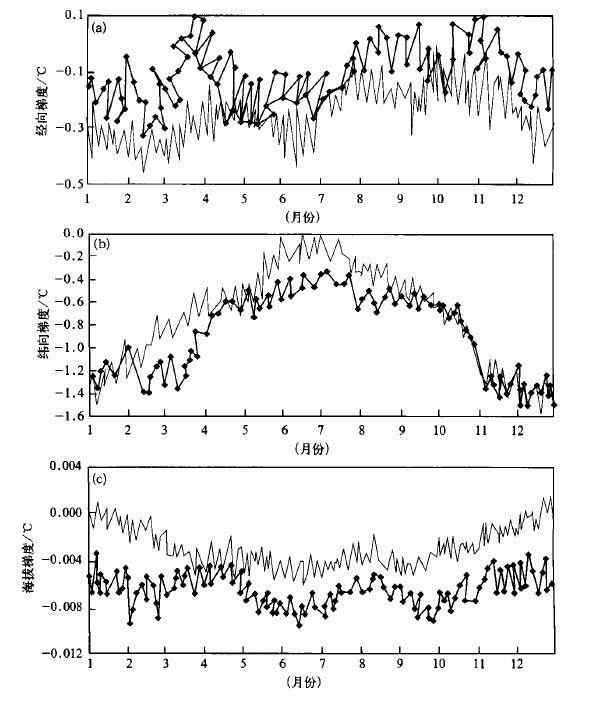
|
|
| 图 2. 日最高温度和最低温度随经向 (a)、纬向 (b) 和海拔高度梯度 (c) 的逐日变化 (—最高温度,-◆-最低温度) | |
逐日降水量随经度增大的量值较小,因季节不同而有增有减。11月至次年4月期间日降水量经向梯度变化平稳,几乎为零,除7月外年内其他大部分时间内日降水量随经度的增大而增多 (图略)。
2.2 纬向梯度及年内变化特征图 2(b)清楚地表明,逐日最高温度和最低温度值随纬度的增高而减少。纬向梯度年内变化呈明显的抛物线特征,7月份南北纬向梯度最小,冬季最大。纬向梯度的年变化幅度以最低温度更大一些。
逐日降水量随纬度的增高而有所减少,但幅度较小。其中以夏季为最明显,冬季日降水量几乎不随纬度而变 (图略)。
2.3 海拔高度梯度及年内变化特征从图 2(c)可以看出,逐日最高温度和最低温度随海拔高度的增加而降低,海拔梯度年变化呈波动特征。最高温度的海拔梯度在1~3月呈直线上升,从0 ℃/100m上升到0.4 ℃/100m;在4~9月最高温度相对平稳,大约在0.4 ℃/100m左右,只有一些小波动; 在10~12月呈直线下降,从0.4 ℃/100m下降到0 ℃/100m。最低温度海拔梯度的年内变化曲线起伏多变,分别在2月中旬、6月中旬和10月上旬出现最大值; 在4月、8月和冬季时段较小。
逐日降水量仅在夏季随海拔高度的增加而有所增多,量级较小 (图略)。
由此可见,年内日温度随海拔高度的变化并不简单地遵从通常的温度垂直递减率0.6 ℃/100m,而是有一定的波动范围。因此,在进行带有高度订正的空间插值时,应当使用动态的温度高度梯度。
3 空间插值结果估值检验与统计量分析以东北地区高温少雨的2000年为例,采用IDW、GIDW和Kriging方法分别对4~10月期间的逐日最高温度和最低温度进行空间插值计算。日降水量资料因考虑到东北地区大部分站点受高度影响不明显,而只使用IDW和Kriging两种方法。评估插值效果时,首先采用估值交叉检验法分析各种插值方法对每日各要素的插值精度,再按月及4~10月全期时段进行平均 (列于表 1、2) 比较其数量大小。其次对随机选取的10组 (天) 结果进行空间数据的统计量分析。另外,还研究了逐日气象要素场插值前后数据空间分布的变化特征,以综合比较3种插值方法的优劣。
|
|
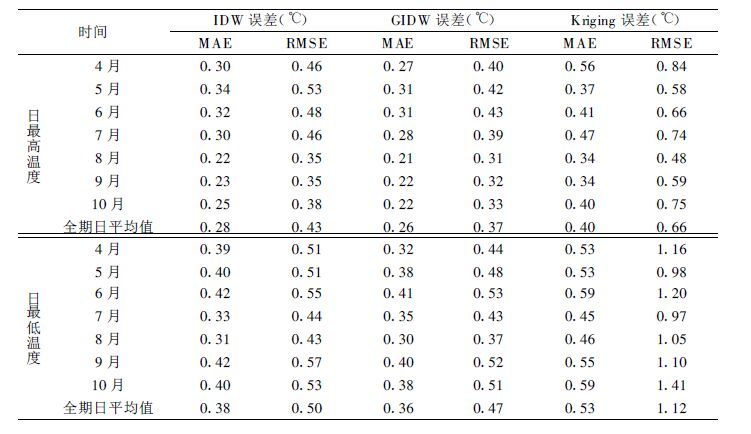
表 1 2000年4~9月日最高温度和日最低温度3种插值方法的估值检验结果 |
|
|
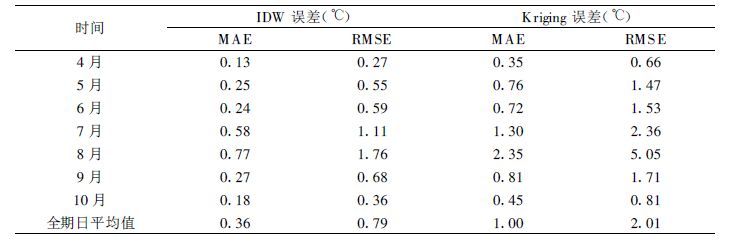
表 2 2000年4~9月日降水量2种插值方法的估值检验结果 |
3.1 插值结果估值检验
从表 1、2来看:插值方法中,温度 (日最高、最低) 的绝对平均误差 (MAE) 和均方根误差 (RMSE) 的大小顺序均为Kriging >IDW >GIDW,如日最高温度的误差 (MAE、RMSE) 分别为0.40 ℃、0.28 ℃、0.26 ℃和0.66 ℃、0.43 ℃、0.37 ℃,其中IDW与GIDW误差的差异较小; 降水量的MAE和RMSE的大小顺序为Kriging >IDW,其值分别为1.00mm、0.36 mm和2.01 mm、0.79 mm。结果表明Kriging方法的误差最大,其估值精度低于其他方法; GIDW因带高度订正而获得最低的MAE和RMSE,比IDW插值估值精度有所提高。
从GIDW和Kriging方法的绝对平均误差与IDW方法的误差的差值随时间 (日) 变化图 (图 3、4、5) 中可以看出:在2000年4~10月作物生长季期间,对于温度而言,GIDW与IDW每日误差的差值大多为负值,即GIDW的日误差比IDW小,但差别较小; 而Kriging与IDW每日误差的差值基本为正值,Kriging的日误差明显比IDW大。对于降水量,Kriging与IDW每日误差的差值均为正值,夏季达到最大,即Kriging的日误差明显比IDW大。
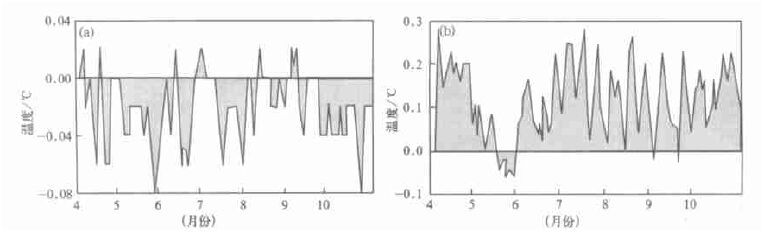
|
|
| 图 3. 日最高温度GIDW (a) 和Kriging (b) 方法的估值绝对平均误差与IDW误差的差值逐日变化 | |
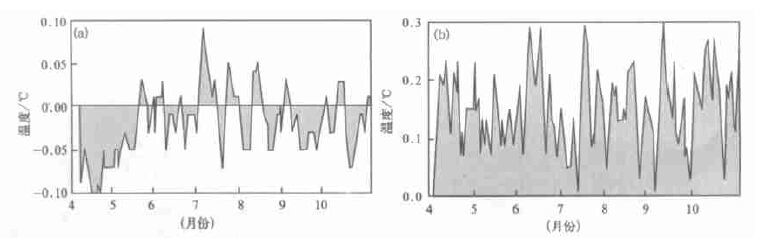
|
|
| 图 4. 日最低温度GIDW (a) 和Kriging (b) 方法的估值绝对平均误差与IDW误差的差值逐日变化 | |
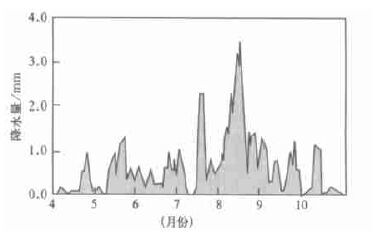
|
|
| 图 5. 日最大降水量Kriging方法的估值绝对平均误差与IDW误差的差值逐日变化 | |
由此可见,在3种插值方法中,Kriging的误差较大,IDW较小,GIDW比IDW又有所改进。
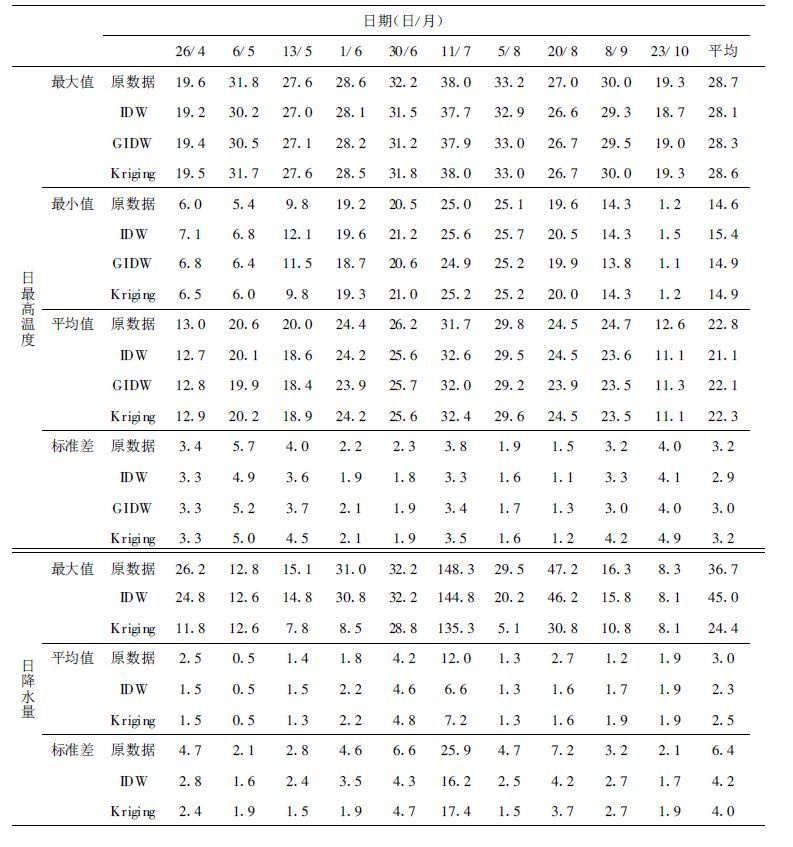
3.2 插值结果的统计量分析从表 3日最高温度插值结果的统计量分析可以看出,3种方法插值结果的最大值有所变小,而最小值变大,导致极差变小,极差排列顺序由大到小依次为Kriging >GIDW >IDW。同时,表 3中的标准差统计结果表明,IDW和GIDW方法插值结果的标准差与原始数据相比有所减小,GIDW稍大于IDW,而Kriging的标准差基本不变,说明IDW和GIDW插值法平滑数据的作用均比Kriging略大。日最低温度也有相似的结论。
|
|
表 3 2000年日最高温度和日降水量插值方法结果的统计量 |
从表 3日降水量插值结果的统计量分析来看,经IDW和Kriging插值结果的最大值变小,最小不变,极差有所变小。同时,2种方法降水插值结果的标准差均明显变小,其中Kriging数据平滑更为明显。
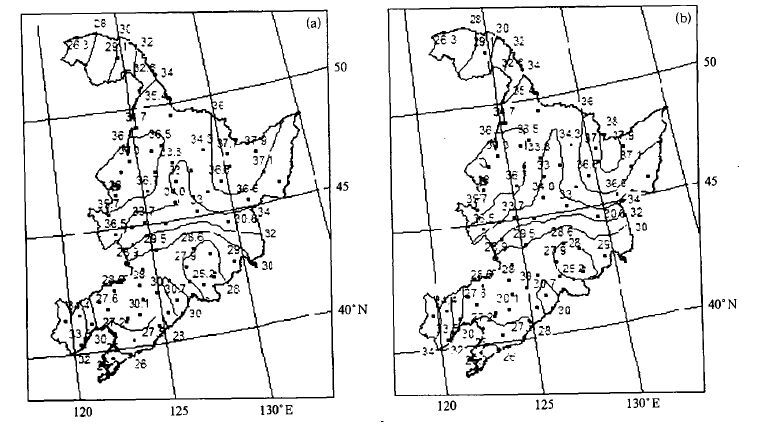
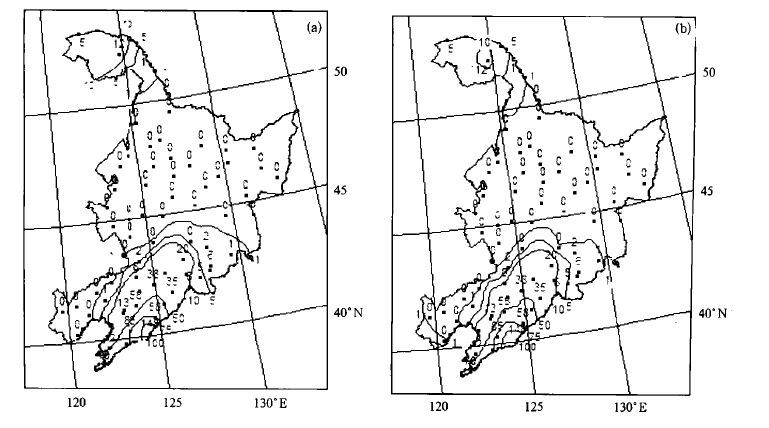
3.3 插值结果空间分布形势对比分析选取2000年7月11日最高温度和降水量插值结果的空间分布形势 (等值线) 与观测站实况分布为例进行对比分析,如图 6、7所示。
|
|
| 图 6. 2000年7月11日最高温度空间插值分布与实测点数据形势对比 (a) GIDW方法 (b) Kriging方法 (图中圆点为样本站点分布,其上方数字为实况值) | |
|
|
| 图 7. 2000年7月11日降水量空间插值分布与实测点数据形势对比 (a) GIDW方法 (b) Kriging方法 (图中圆点为样本站点分布,其上方数字为实况值) | |
从图 6日最高温度分别用GIDW和Kriging方法插值后的等值线分布来看,GIDW曲线稍微平滑,但2种方法插值后的温度分布形势十分相似,高低温区域没有发生漂移,均在黑龙江西部佳木斯、东部齐齐哈尔出现高温区和辽宁南部大连、黑龙江北部漠河形成低温区域,且与样本点相吻合。
图 7中7月11日的降水量主要集中在吉林南部、辽宁大部和黑龙江北部部分地区,降水从吉林西南部向辽宁东南倾斜逐步增多,在辽宁丹东形成大雨中心。两种插值方法的结果来看,降水空间分布形势一致,大雨中心没有发生漂移,与实况样本分布也较吻合。
4 结论与探讨(1) 通过对东北地区逐日气象要素的纬度、经度梯度及其年内变化特征分析,可以看出:日最高、最低温度纬向梯度的年内变化呈明显的抛物线特征; 日降水量随纬度的增高而有所减少,夏季最明显。日最高、最低温度随经度增大而下降,且年内有明显的起伏波动,冬季梯度大于夏季; 日降水量随经度增大的量值较小。日最高温度随海拔高度梯度年内变化范围为-0.1 ℃/100 m~-0.6 ℃/100m,夏高冬低; 日最低温度的高度梯度年内变动范围是-0.4 ℃/100 m~-0.9 ℃/100m。因此,在利用距离权重反比法进行空间插值计算时除距离外还应根据气象要素在经度、纬度的分布方向确定权重; 在结合海拔高度影响进行插值订正时应考虑气象要素高度梯度在年内不同时间的变化。这也是本研究改进的IDW和GIDW插值效果较好的原因所在。
(2) 对东北地区逐日气象要素插值结果进行的统计量分析和估值交叉验证以及插值结果的空间分布形势分析,结果表明:Kriging、IDW和GIDW方法均具有平滑数据的作用,但其插值结果的空间分布形势基本保持不变。相比之下,对温度而言,考虑经纬度方向权重的IDW和带高度订正的GIDW具有较高的估值精度,插值结果的平滑程度适中,分布趋势也接近实际状况,更为合理; 而Kriging方法虽然平滑数据程度稍小,但估值精度低,不如IDW和GIDW方法。对降水而言,IDW估值精度仍高于Kriging,而且插值结果的平滑程度较小,更适合于日降水量的空间插值。综上所述,对于时间、空间变幅较大的日最高、最低温度和日降水量,IDW和GIDW方法具有较高的估值精度,而且计算简单,可以满足区域作物生长模型的需要。
(3) 采用1:25万DEM高程数据修正的GIDW方法比简单的IDW的估值精度有所提高,插值结果分布趋势较为合理。但需要指出是高程数据的精度对GIDW有影响,例如使用1:100万DEM高程数据做订正时插值精度会下降。因此,选择精度较高的DEM高程数据十分重要。
(4) Kriging以最佳线性无偏差估计而在地统计学中得到应用,但诸学者[4、7]的研究迹象表明,Kriging可能比较适合于区域性差异较大或多因素综合影响的因子,而对于单一因素影响的因子的插值,IDW比较适合,估值精度较高,这与本研究的结论相似。但是,由于区域范围、气象要素种类及其时间尺度的不同,造成数据的时空变异特征不同,其空间插值方法也不尽相同,应当根据插值数据的特征、插值对精度的要求以及计算试验效果分析等因素综合选择合适的插值方法。
| [1] | 尚宗波, 高凉, 杨奠安. 利用中国气候信息系统研究年降水量空间分布规律. 生态学报, 2001, 21, (5): 689–694. |
| [2] | 周锁铨, 缪启龙, 吴息, 等. 日照百分率的小网格分析方法. 气象科学, 1993, 13, (2): 201–209. |
| [3] | 王绍强, 朱松丽, 周成虎. 中国土壤土层厚度的空间变异性特征. 地理研究, 2001, 20, (2): 161–167. |
| [4] | 李海滨, 林忠辉, 刘苏峡. Kriging方法在区域土壤水分估值中的应用. 地理研究, 2001, 20, (4): 446–452. |
| [5] | 梁天刚, 王兮之, 戴若兰. 多年平均降水资源空间变化模拟方法的研究. 西北植物学报, 2000, 20, (5): 865–862. |
| [6] | 魏凤英, 曹鸿兴. 我国月降水和气温网格点资料的处理和分析. 气象, 1994, 20, (10): 26–30. |
| [7] | 林忠辉, 莫兴国, 李宏轩, 等. 中国陆地区域气象要素的空间插值. 地理学报, 2002, 57, (1): 47–56. |
| [8] | 汤国安, 赵牡丹. 地理信息系统. 北京: 科学出版社, 2002: 117-118. |
 2003, 14 (5): 605-615
2003, 14 (5): 605-615