随着观测手段的日益丰富和计算机软硬件水平的飞速提高,数值模式在天气预报业务中得到了越来越广泛的应用。但是由于数值预报结果受模式初值场、边界条件、物理过程、地形、植被及模式本身的设计等诸多方面的影响,模式输出产品不可避免地会存在一定的误差。数值预报模式的检验正是对模式预报误差,即预报产品和相应的观测数据集二者相互关系的评估及量化。了解模式预报误差的时空分布特征无论对于模式用户还是研发人员都是十分有益的。一方面可以检验模式性能在空间/时间上的差异,向模式研发者提供反馈信息,有助于模式研发人员诊断和修正模式物理参数化中可能存在的缺陷; 另外还为预报员订正预报结果提供客观依据,如Homleid (1995)[1]和Stensrud and Skindlov (1996)[2]指出,发展本地化实时订正可分辨模式误差的技术可以提高客观定点预报的准确率,因此它对于数值预报产品的释用起到了重要的决策作用。
北京地区中尺度数值预报业务系统从1999年就已开始运行,数值预报模式是基于PSU/NCAR发展的非静力中尺度数值模式 (MM5V2),模式水平分辨率为15 km,清华同方集群计算机提供了主要的运行环境。通过近两年多的运行和业务预报发现,该预报系统性能稳定,预报结果对业务预报有一定的参考意义,并在北京重大政治文化活动的气象服务和保障中发挥了重要作用,同时也积累了大量的数值预报产品和实况资料。尽管已有多年的模式运行经验,但是对模式预报产品质量一直缺乏客观的评价。为了对模式性能和预报效果形成较为客观全面的认识,并进一步为数值预报产品的统计和动力释用提供基础,北京市气象科学研究所开发建立了北京地区中尺度气象预报产品的客观检验系统。本文将对该系统的框架、方法等作出详细的介绍,并且将着重分析北京地区主要预报产品的检验结果,然后给出2001年冬季北京地区中尺度数值预报业务的误差分布特征。
1 客观检验系统目前中尺度数值模式的客观检验系统已在北京市气象局投入准业务运行。该系统提供了对中尺度数值业务模式 (MM5) 的形势场预报统计检验,其中包括两方面内容,一是以客观分析资料为实况对网格点上的预报产品进行的检验,即预报场相对分析场的检验; 另一部分是用探空和地面观测资料为实况,对插值到测站上的预报产品进行检验,即预报相对观测的检验。
1.1 用分析资料检验预报效果客观检验实况场的产生与数值预报业务系统前处理的客观分析类似,但08:00(北京时,下同) 和20:00实况的初估场分别由T106的12h预报场和T106在20:00的分析场插值到中尺度网格点上生成,然后加入常规高空资料对初估场进行再分析后产生检验系统的实况场。由于预报时效为36h,每天获得当日的观测实况后只能对两天前的预报进行检验。而且受每天只有两次高空观测报文的局限,检验时效也只能为00、12、24、36 h的预报。检验要素为海平面气压、位势高度、温度、风和比湿; 检验层次为1001 hPa、850hPa、700 hPa、500 hPa、300 hPa.另外还包括了对2-m温度和10-m风的检验,但2-m温度和10-m风的实况场由T106预报场经地面温度和风的观测值修正后再插值到中尺度网格点上诊断生成。检验区域覆盖了业务模式第二层嵌套网格的全部范围。
1.2 用观测资料检验预报效果利用业务模式网格范围内的基准探空和地面站观测资料为实况,将网格点预报值线性内插到站点,再与观测资料进行比较并计算区域评分。其中检验区域内有约30个探空观测站和800个左右的地面观测站 (图 1).检验要素、检验时效、检验层次和区域均与全场格点检验一致,地面温度和风的观测直接用于检验2-m温度和10-m风。另外,对于预报员更为关注的单站 (如北京,54511测站) 输出要素的预报值与观测值对照表,以便于进行单站进一步的时间序列检验,总结单站预报误差的时间分布特征。

|
|
| 图 1. 检验区域内高空和地面测站分布 | |
1.3 检验统计量
该系统计算的检验统计量包括平均误差、均方根误差、误差标准差、位势高度的SI评分以及倾向相关系数。
1.4 检验系统运作流程检验系统每天运行一次,对08:00的业务预报结果进行检验。其业务流程分为资料采集、检验量计算和输出显示三个部分。资料采集部分从存储器中调用制作实况场和待检验数据集的T106资料、高空和地面观测资料和业务预报输出数据; 生成全场格点和测站检验的实况场及预报场后,由检验量计算部分分别进行分析和测站检验; 最后将检验结果以文本文件的形式输出,并由MICAPS图形显示各预报要素在网格点上的偏差 (即预报值-观测值).具体的运作流程见图 2。

|
|
| 图 2. 客观检验系统的业务流程 | |
2 北京地区中尺度数值业务预报的误差分析 2.1 资料和方法
客观检验系统从2001年9月起开始试运行。北京地区冬季 (2001年11月1日~2002年2月28日) 的预报检验结果积累得相对完整。排除由于T106资料缺失造成模式未能正常运行以及观测资料不全导致检验出错的个别天数,总共获得了113个检验样本。待检验地面要素包括10-m风速、2-m温度,高空要素包括了风速、温度、位势高度和比湿,待检验的气压层为850 hPa、700 hPa、500 hPa和300 hPa.针对上述要素将分别给出全场平均格点误差分析结果以及北京 (54511) 单站的误差特征。
本文中用于量化模式预报误差的统计量包括预报平均误差 (bias,即预报值-观测值)、均方根误差和误差标准差。必须认识到模式误差中包含了系统性和非系统性误差 (见附录),其中预报平均误差表示了模式的系统性误差分量,它是真实大气环境和模式大气环境之间的差异 (诸如地形、辐射、对流等过程在模式中不可能得到完全正确的描述) 造成的; 非系统性误差由误差标准差来衡量,代表了由初始条件的不确定性以及观测和预报之间分辨率尺度不一致等造成的随机性误差。对模式误差的统计结果进行分析,有助于定性地判断预报误差的可能来源。
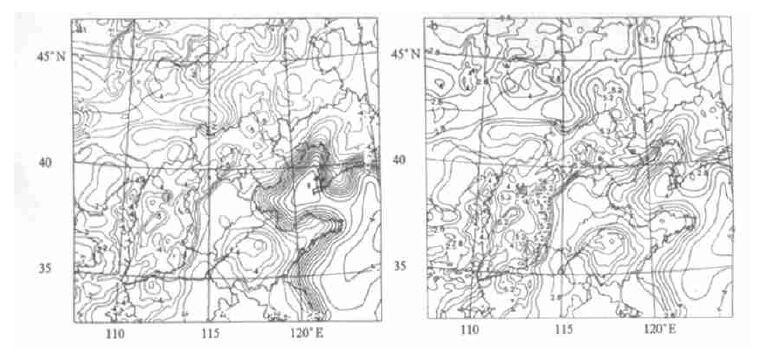
2.2 格点平均误差分析全场格点检验提供了数值模式预报天气形势能力的客观评估。对模式全场每个格点的时间序列进行统计获得了全场预报在空间上的误差分布特征。图 3分别给出2-m温度在36h的平均误差和均方根误差等值线。很明显,海面上温度预报显著偏高2~4 ℃,可能是因为模式采用海温的气候平均值制作初始场导致的系统性误差。另外,除了海上以外陆地的整场格点预报值均低于实况。而且与图 4所示的模式地形高度分布相比较后不难看出,温度的误差等值线与模式地形高度分布有密切的相关,即在高地形区似乎更容易出现较大的温度误差,而地势较为平坦的地区温度平均误差较小且分布均匀。例如南北走向的太行山脉就与密集的误差等值线吻合得很好。北京东南部地形平坦,西北部为山区,实际海拔高度最高可达到1500m以上。相应地,2-m温度平均误差在北京西北部最大,比实况低了约5 ℃; 相反在北京的平坦地区迅速减至2 ℃左右,即地形高度从高到低的过渡带对应了2-m温度平均误差梯度最大的区域。或者更确切地说,似乎在高地形的背风坡方向更易产生较大的温度平均误差梯度。由于地形在数值模式中对模拟结果的影响有着固定的强迫作用,对于12 h、24 h、36h预报的检验结果 (图略) 中均可以找到这种地形高度和温度平均误差的相关。而且,比较图 3中2-m温度平均误差和均方根误差等值线分布,二者无论大小和分布形势均十分吻合。因此可以认为2-m温度的预报误差很大一部分来自由平均误差代表的系统性误差,而其中地形的影响是造成这种系统性误差不可忽略的重要来源。
|
|
| 图 3. t=36h时2-m温度的平均误差 (a)(负值为虚线,等值线间隔为0.5 ℃) 和均方根误差 (b)(等值线间隔为0.5 ℃) | |

|
|
| 图 4. 模拟区域内地形高度的等值线分布 (等值线间隔为100 m) | |
由于模式地形高度由精度为10分的全球地形资料插值而得,不可避免地受到一定程度的平滑,不可能完全真实地反映实际的地形状况。一般认为,地形细节在数值模式中的表述往往为中尺度现象的产生提供固定的强迫机制。但是全场格点误差统计结果表明,不仅仅是近地面预报要素,中高层的形势分布也很大程度地受到了模式地形分布的影响。例如,700 hPa温度平均误差的等值线 (图 5a) 呈现出与地形走向密切的相关,即高地形区偏暖 (或相对较小程度地偏冷).这一方面可能是由于高地形对高空的实际增暖效应未能由观测系统分辨出来,也有可能是高分辨率模式在处理高地形区域时的系统误差,即模式地形往往低于实际地形,这在高地形区尤为明显,因此导致高地形区的暖偏差。另外,700 hPa的位势高度、风速、比湿场的平均误差具有与温度十分类似的误差特征 (图略).这说明地形的强迫作用在很大程度上也是对流层中层系统误差的重要来源。但是在分析700 hPa温度的均方根误差和误差标准差 (图 5b,图 5c) 后可以发现,非系统性误差分量的大小和分布与均方根误差更为相似。因此高空要素预报全场误差主要由非系统性误差造成。值得注意的是模拟区域的西边界附近为误差标准差的大值区,这可能是边界条件带来的误差向积分区域内传递的结果。另外,误差标准差和均方根误差的分布均出现一些尺度较小的误差中心,这有可能是基于低分辨率背景场和高空观测资料的实况分析场与模式输出之间分辨率的差异导致的。

|
|
| 图 5. t=24h时700hPa温度的平均误差 (a)(负值为虚线,等值线间隔为0.07℃) 均方根误差 (b)(等值线间隔为0.1℃) 和误差标准差 (c)(等值线间隔为0.1℃) | |
2.3 测站平均误差分析
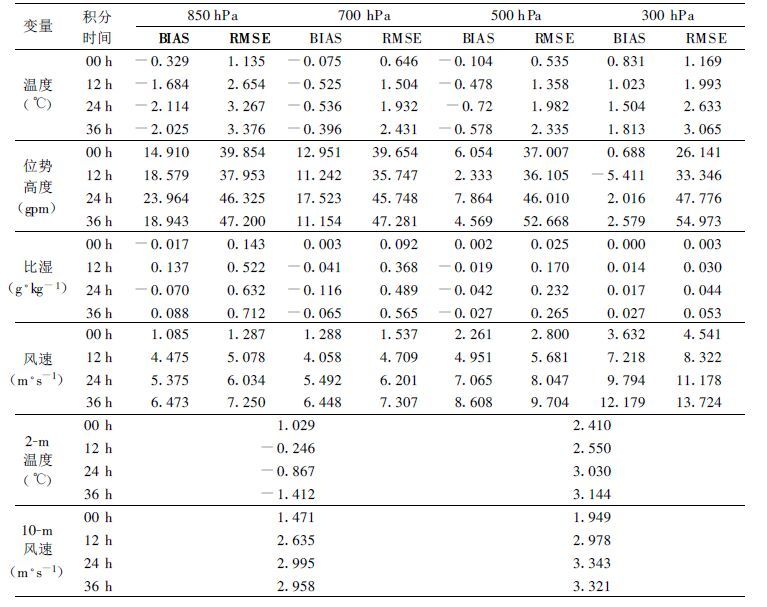
对测站预报误差进行检验,其目的是研究数值模式在特定空间位置上的整体预报能力。因为模式在特定测站位置上的预报产品为预报员进行定时定点预报提供了最直接的参考,因此定点预报的客观检验是模式性能最关键的度量指标之一。表 1给出了高空温度、位势高度、比湿、风速以及地面10-m风速和2-m温度的平均误差和均方根误差。分析00:00的检验结果可以发现各气压层测站要素的初始值就已存在误差,其中温度的平均误差在1 ℃以下,低层位势高度的平均误差量级约为10 gpm,而风速的平均误差随高度向上从1 m·s-1增大到3 m·s-1左右。初始时刻各变量的均方根误差更为显著,其中位势高度的均方根误差达到了35 gpm以上,或许这是因为位势高度由模式诊断输出的缘故。这种误差很大程度上反映的是初始时刻分析场和实况观测之间的差异,一方面由于模式的初始场由背景场经测站订正后获得,它与测站的实况值之间不可能完全地吻合; 另外在从模式格点向测站进行插值的过程中也不可避免地出现误差。
各变量的均方根误差随着积分时间持续增长,即初始时刻的误差在积分过程中被持续放大。其中到t=36h时位势高度和温度的均方根误差分别增大到47~55 gpm和2.3~3.3 ℃,而风速均方根误差增大到7~13 m·s-1以上。2-m温度和10-m风速到t=36 h时均方根误差也分别达到了3.144 ℃和3.321 m·s-1.根据表 1给出的结果可以得到对MM5模式业务预报能力的初步印象,即模式的预报能力随积分时间递减,而且位势高度和风的预报似乎并不理想。尤其是36h时300 hPa风速的均方根误差达到了13 m·s-1以上,这意味着将在12h内产生400 km以上的平流误差,相当于1600 km左右尺度的天气系统在12h内就产生1/4波长以上的位相差。因此模式对对流层高层的预报能力是有欠缺的。
|
|
表 1 测站的平均误差 (BIAS) 和均方根误差 (RMSE) |
需要指出的是,表 1给出的检验结果在相当程度上反映了MM5模式预报能力的普遍状况。White等 (1999)[3]比较了包括MM5在内的六个数值模式的短期预报能力,给出的MM5高空要素预报检验结果与本文具有相似的量级。特别是对流层高层风的预报,所有的数值模式均有很大的误差,这是业务数值预报面临的共同难题。
2.4 北京 (54511) 测站的误差特征分析表 2给出了北京 (54511) 站2-m温度在00 h、12 h、24 h、36h的平均误差、均方根误差和误差标准差。由此可见2-m温度的冬季预报整体偏低。其中在预报的起始时刻 (00h,相当于北京时的上午8:00) 的平均误差只有-0.88 ℃,但均方根误差和误差标准差分别达到2.85 ℃和2.71 ℃,说明在该时刻非系统性的随机误差是2-m温度平均误差的最主要来源。这种随机性误差在2-m温度预报值和观测值的散布图 (图 6) 上表现得十分清楚。在图 6a上发现,大的误差值更容易发生在0 ℃以上的观测,负最大平均误差可达10 ℃以上。很可能这是由于模式在制作初始场时由于背景场地面温度比实况偏低太多,导致观测值未能对背景场进行有效订正而造成的。另一方面,插值方法和2-m温度的计算过程均是误差的可能来源。
|
|
表 2 北京 (54511) 站2-m温度和10-m风速平均误差 (2001年11月1日~2002年2月28日) |

|
|
| 图 6. 北京 (54511) 站2-m温度预报值相对于观测值的散布图 (a) t=00 h, (b) t=12h,(c) t=24h,(d) t=36 h (2001年11月1日~2002年2月28日,共110个样本) | |
从12h到36h,2-m温度的预报平均误差进一步增大,但是误差的组成发生了变化。在12h仍然是非系统性误差为主; 24h的平均误差增至-2.2868 ℃,但仍然小于2.65℃的误差标准差; 到36h,平均误差则明显超过了误差标准差。这表明随着积分时间增长,由模式本身造成的系统性误差逐渐变得重要。若系统性误差占主导地位,采用统计方法进行一个简单的平均误差订正就可以使预报效果得到极大的提高[2].例如,36h的平均误差为-2.29 ℃,因此在该时刻的2-m温度预报值和观测值的散布图上 (图 6d) 将曲线y=x向上平移2.29 ℃即可发现,大多数样本点均可以落在±2 ℃的预报精度范围内。但是对于随机误差为主的情形,采用这种方法进行订正远远不够。如图 6c所示的24h,订正平均误差后仍然有相当多的样本落在预报精度范围之外。
从对10-m风速的误差统计结果 (表 2) 来看,预报风速明显高于实况值。但其中随机误差是最主要的误差来源。这是易于理解的。一方面这种误差由于观测精度不够造成,因为实况观测风速代表的是单个空间点上的状况,模式的预报输出量为网格范围内的平均值; 而且观测风速在报文中以整数表示,这些都是潜在的误差来源。
现有的每3h一次地面观测资料始于1月21日,因此对本研究而言仅有39天的长度,虽然不足以代表整个冬季的平均状况,但仍然有助于分析1月下旬和整个2月预报误差的日变化特征。图 7a给出了每3h一次地面观测温度和预报2-m温度的平均值在0~36h预报周期内的分布。很明显,2-m温度预报较好地反映了气温的日变化状况,即下午14:00到17:00出现最高气温,温度从17:00开始逐渐下降,并在早上08:00达到最低。与上文给出的预报平均误差类似,2-m温度预报在整个预报周期内均低于实况。分析预报误差的组成 (图 7b) 不难看出,误差标准差在积分的前6个小时内迅速减小然后保持相对稳定,而积分至6小时以后的均方根误差与平均误差具有极为相似的分布形态,表明温度预报误差的日变化主要是系统性误差的日变化导致的,其中夜间 (12~24 h) 的预报平均误差显著小于白天 (0~12h,24~36 h).考虑误差标准差及平均误差的相对大小,夜间非系统性误差略大于系统性误差,但白天系统性误差是最主要的误差来源。

|
|
| 图 7. 北京 (54511) 站从2002年1月21~2月28日的 (a)2-m温度预报 (虚线)、地面温度观测 (实线) 和预报-观测 (点线) 的平均日变化,(b)2-m温度预报的均方根误差 (实线)、平均误差 (虚线)、误差标准差 (点线) | |
造成2-m温度误差的因素多种多样,其中系统性误差的日变化往往被认为与模式的辐射方案有关。例如在Eta模式中过量净短波辐射间接导致了白天地面温度的系统性误差,因此NCEP有针对性地对辐射方案进行了专门的修正[4].另外,任何一种行星边界层的物理参数化方案都只是发生在地表附近复杂大气过程较大程度的近似,边界层中的扰动是高度随机的,这也是造成温度预报随机误差的一个重要因素[5].除此以外,2-m温度的计算过程、插值方法等等都有可能带来近地面要素预报的随机误差。尤其是模式地形的不真实性往往会在垂直插值计算地面要素预报过程中产生较大的误差。
3 讨论和结论本文对北京地区2001年冬季113个样本的中尺度数值预报结果进行了检验,可以获得以下初步结论:
(1) 格点地面要素预报以系统性误差为主,而地形的强迫作用是预报系统性误差的一个重要来源。格点高空形势预报的系统性误差也反映了地形的影响。
(2) 测站高空要素预报的非系统性误差显著,其中尺度较小的误差中心很可能是由于模式输出与背景场和高空观测网之间分辨率的高低差异造成的。从测站预报的平均误差分析结果可以发现,初始场的误差在积分过程中往往会被进一步放大。而且位势高度和风等预报要素的检验结果表明有限区域中尺度模式对于较大尺度天气系统的预报能力存在一定的缺陷。
(3) 分析北京单站地面要素预报的检验结果发现,2-m温度预报冬季整体偏低。但在系统性误差为主要误差分量时对模式的平均误差进行订正能有效地提高温度预报的准确率。地面温度预报误差的日变化应该可以通过调整模式中相应物理过程来得到改善。
数值模式的检验结果和上述结论表明,进一步提高数值预报质量,必须做到数值模式本身的继续完善和数值预报产品的统计释用二者并重。另外,提高初始场的质量也是改善数值预报效果的重要方面。目前北京市气象局已采用卡尔曼滤波方法制作北京地区温度和风的预报,并取得了良好的效果[6].而且采用变分方法同化非常规资料以提高模式初始场质量的研究也已处于起步阶段。
应当看到,上文中对于误差的分析方法仍然是比较粗糙的,尤其是无法进一步区分出与系统性误差有关的具体物理过程。而且一方面由于实况的背景场采用了T106的预报结果来制作,不可避免会受到T106模式预报误差的影响; 另外,高空观测资料分辨率也相对较粗,这种条件下获得的`实况'场与大气的真实状况必然存在一定的差别。其结果也有可能低估了中尺度有限区域模式的可用性。因此对于具有稠密自动站以及雷达、风廓线观测网的地区而言,使用这些时空分辨率更高的实况资料进行检验可能更有意义。
| [1] | Homleid M, Diurnal corrections of short-term surface temperature forecasts using the Kalman filter. Wea, Forecasting, 1995, 10: 689–707. DOI:10.1175/1520-0434(1995)010<0689:DCOSTS>2.0.CO;2 |
| [2] | Stensrud D J, Skindlov J A, Gridpoint predictions of high temperature from a mesoscale model. Wea, Forecasting, 1996, 11: 103–110. DOI:10.1175/1520-0434(1996)011<0103:GPOHTF>2.0.CO;2 |
| [3] | White B G, Paegle J, Short-term forecast validation of six models. Wea, Forecasting, 1999, 14: 84–108. DOI:10.1175/1520-0434(1999)014<0084:STFVOS>2.0.CO;2 |
| [4] | Black T L, Coauthors. Changes to the Eta forecast systems. NWS Tech. Proc. Bull, 441. National Oceanic and Atmospheric Administration/National Weather Service, 1997: 16. |
| [5] | Mao Qi, McNider R T, An optimal model output calibration algorithm suitable for objective temperature forecasting. Wea, Forecasting, 1999, 14: 190–202. DOI:10.1175/1520-0434(1999)014<0190:AOMOCA>2.0.CO;2 |
| [6] | 王迎春, 刘凤辉, 张小玲, 等. 北京地区中尺度非静力数值预报产品释用技术研究. 应用气象学报, 2002, 13, (3): 312–321. |
 2003, 14 (5): 522-532
2003, 14 (5): 522-532