暴雨是大、中、小尺度天气系统相互制约并由中小尺度系统直接引发的产物[1]。从这一天气学的观点出发,要取得有效的暴雨预报模型,首要问题是要解决好对影响系统的切实、客观和定量的表征。
切比雪夫正交多项式能够对要素场的内在特征信息进行定量化提取,生成彼此相互独立的场量因子[2]; 滑动分区展开技术可对场信息做极限化的开发[3],产生多种尺度的特征信息,极大地丰富信息来源和提高信息质量,为预报研究提供更为完备的信息环境,从而获得对预报目标成因更完备的认识。
基于此,本文一改我省以往同类研究主要以单点要素值为信息源的方式,以滑动分区切比雪夫展开方法,求取具有二维空间尺度特征的场量因子———高度场特征分布的展开系数及其时间变量,做为建立暴雨预报模型的信息源。通过相关分析,从中提取物理意义明确和相关性好的预报因子集和消空因子集,再通过预报因子的多态组合分析,提炼出物理图像清晰的福建省前汛期区域暴雨预报模型。
实际效果证明,这种改进的技术路线是具有成效的。据此而得的预报模型在2000、2001年的试用中准确率稳定在80 %的历史水平,且有保持不漏报的能力; 在很干旱的2002年5、6月份的实用中,仍保持不漏报的历史水平,并成功报出6月11~18日的特长连续性区域暴雨,预报效果优于主观预报。
1 暴雨的气候概率规定福建省境内66个测站中,凡同一天出现当日20:00~次日20:00的24小时雨量≥50 mm的站数≥5站的现象,称为“区域暴雨”。
在1990~1999年的前汛期 (即5~6月),符合定义的区域暴雨个例有87次,其中5月30次,6月57次。由此可见,5月与6月的区域暴雨气候概率 (P0) 有明显的差别,5月仅为9.7 %(样本长度为310天),而6月则达19 %(样本长度为300天),后者为前者的2倍。这表明,区域暴雨的生成背景 (形势特征)5、6月间可能颇有差别。鉴于此,研究中,对5、6月份的区域暴雨分别进行分析与建模。
在相关分析中预报量作二值化处理,即取有“区域暴雨”为“1”,记为“y=1”,称“正例”,反之为“0”,记为“y=0”,称“反例”。
2 展开系数的计算和滑动分区 2.1 切比雪夫展开系数的计算取用下式[4]:
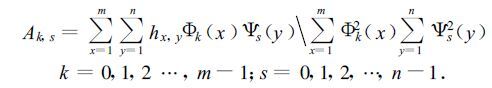
|
(1) |
式中hx,y为在格点 (x、y) 上的要素值,在本研究中取为等压面的高度; m为展开场的列点数; n为展开场的行点数; Φk(x) 为沿x方向最简整数化[4]的第k阶切比雪夫正交多项式,它由
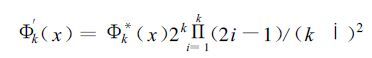
|
经约简而来; Ψs(y) 为沿y方向整数化[4]的第s阶切比雪夫正交多项式,它由
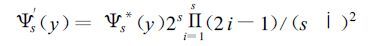
|
经约简而来,约简算法见文献[5]; Φk* (x),Φk*(x) 为常义的切比雪夫正交多项式。Ak,s为要素场的k×s阶特征场的权重系数,简称为“k×s阶展开系数”。注意到高阶特征场的天气学意义不明确,本文只取k,s≤2的前9个低阶特征场的展开系数。
若把各个二维特征场的数值分布形态[2]视为等压面上的hh分布形态,则由天气学中的风、压关系易知,各个“k×s”特征场的天气学意义分别是:“0 ×0”阶特征场体现均压场; “0 ×1”阶特征场体现纬向气流的存在; “0 ×2”阶特征场体现气流的纬向切变存在; “1 ×0”阶特征场体现经向气流的存在; “1 ×1”阶特征场体现鞍形场结构的存在; “1 ×2”阶特征场体现东部低压系统的存在; “2 ×0”阶特征场可体现气流的经向切变存在; “2 ×1”阶特征场体现南部低压系统的存在; “2 ×2”阶特征场体现中部高压系统的存在。
Ak,s实质上是要素场中具有k×s阶特征场这种分布特征的“权重”。所以Ak,s具有与之相应的k×s阶特征场等价的天气学意义,因此其值即是要素场中相应特征分布之天气学意义的量化体现,如A0,1<0表示要素场的分布趋势具有北高南低的特征,其绝对值越大,北高南低的特征就越突出,反之亦然。因而可为天气预报分析提供客观、定量化的信息依据。这就是本项研究引用之原理所在。
2.2 滑动分区滑动分区技术指在一个选定的大尺度基本场上,以次尺度 (网格) 场做自西向东的逐列和自北向南的逐行有序平移的方式划分次尺度展开场的方法[3]。
这种技术的优点是可以把一个大尺度场分解成网格尺度为ni ×mi的Si个不重叠的分区:
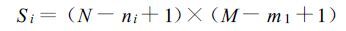
|
式中N、M分别为基本场的行数和列数; ni、mi分别为第i种次尺度场的行数、列数,ni≤N,mi≤M。
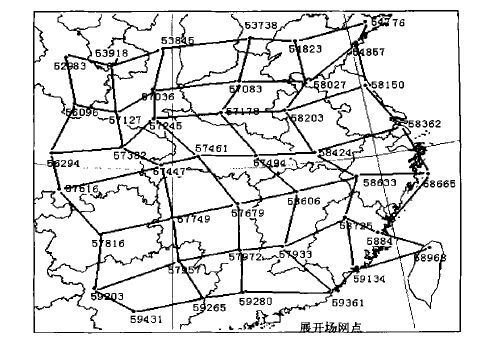
本研究中基本场网格为7行×6列,见图 1。对其进行4 ×4、4 ×5、5 ×4、5 ×5、5 ×6、6 ×5、6 ×6等7种次尺度网格场的滑动分区,共得44个不相重合的次尺度展开场,显然,这样的基本场足以捕捉到影响福建省的所有西风带天气系统。
|
|
| 图 1. 基本场网格设置 | |
3 获取的基本信息量 3.1 可开发的场量因子
对基本场及上述44种分区计算样本3层08:00实况高度场的前9个低阶展开系数,共得1215个互不等价的展开系数 (场量因子),并计算其时间变量,则每月均合计有2430个可供分析之用的场量因子。
3.2 Ak,s时间变量的计算Ak,s时间变量是指其在Δt=t0-t-1时间内其值的变化量,定义为:
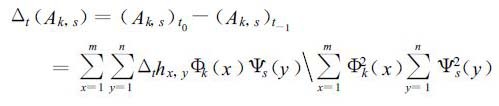
|
(2) |
式中Δthx,y为要素变量,本文指等压面上的变高。故式 (2) 表明,展开系数时间变量实质上即是要素之变量场的展开系数。因此,它能从动态的角度客观、量化地揭示要素场随时间演化的特征,也是一类可用的因子。如当Δt(A1,0)>0时,它预示着要素场的分布在总体上发生了“东高西低”增强的变化; 当Δt(A1,0)<0时,则预示着要素场的分布在总体上发生了“西高东低”增强的变化。对于等压面上高度场而言,前者会产生气流的南风分量加大,后者会产生气流的北风分量加大的效应,且其值越大,变化越烈。
3.3 入选的因子通过排序分析将具有“相关区间”(指报“y=1”的条件频率大于数倍区域暴雨气候概率P0的区间) 的系数因子xi的值域划分为若干区间,再做相关测评[6]筛选,选取规则为:
(1) 因子xi在取值域[a,b] (即“相关区间”) 内的条件频率须满足
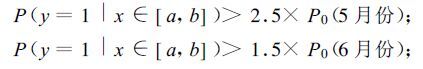
|
(2) 在[a,b]内,正例数
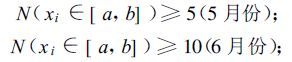
|
(3) 在[a,b]内,正例年份的分布跨度 (指最晚年与最早年之差) 都取≥7年;
(4) xi相关指数[6]Rfi, y要能通过信度为0.01的显著性检验,都取>0.250。预报因子选取结果列入表 1。
|
|
表 1 各月选用的各类因子数 |
4 预报模型 4.1 预报模型的初选
由计算机对表 1的各类因子集进行客观组合计算,普查各种可能的组合模型,按照 (1) 组合模型的因子数要小于等于3个; (2) 组合模型中y=1的个例数,5月要大于等于5,6月要大于等于10;(3) 组合模型的准确率,5月要大于55 %,6月要大于65 %这三条规则,从中初选出符合条件的组合模型。5月有67个,6月有163个。
4.2 实用预报模型通过对初选组合模型的3层平均形势场的比较分析,从中挑选出3层平均形势场的特征具有明确天气学意义的组合模型,再分析它们之间的历史拟合的互补性,按总体历史拟合不漏报、引用组合模型数尽可能少的原则,再从中挑选出“最满意”组合模型,组成实用的预报模型集。
预报模型集中展开系数因子按如下方式表示:
要素代号 (2字)+等压面代号 (1字)+场代号 (1字)+场网格行列标记 (2字)+特征场标记。
如:hh8c44(0,2),其中,“hh8”表示850 hPa高度场; “c44”表示场代号为“C”,展开场尺度为4行×4列的网格场; “(0,2)”表示“0 ×2”阶特征场。所以“hh8c44(0,2)”表示场代号为“C”,展开场尺度为4行×4列网格场的850 hPa高度场的“0 ×2”阶特征场系数因子。系数因子前的标记“d:”或“b:”,分别表示“静态型因子”或“动态型因子”,即时间变量因子。5月预报模型集 (表略) 的历史预报准确率5月在56 %~80 %; 6月在74 %~100 %。
4.3 预报模型的消空因子消空因子选取规则为:
(1) 因子xi在消空区间[c0,c1]内的条件频率须满足

|
(2) 在[c0,c1]内,反例数
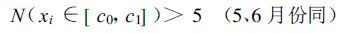
|
(3) [c0,c1]的取值仅限两种方式,或是 (-∞,C),或是 (C,∞),即仅取极端值域。C为有限值。
(4) 在[c0,c1]内,反例年份的分布跨度都取≥7年。
这里“y=0”(即反例) 是指24 h (20:00~20:00) 全省暴雨站数在5月≤2站,在6月≤3站的“事件”。可见消空标准提高了。
消空因子选择中,首先考究的是因子的消空能力及其是否具有不利强降水发生的物理内涵,其次再是其对组合模型中的空报个例的消空能力。因此,在选取的消空因子中,包含有“多余”的因子,即对组合模型中的历史空报个例不起消空作用的因子。
我们制作了福建前汛期5月消空因子取值区间及其对应的个例数和消空数 (表略)。
4.4 逐日预报判别方程及其历史准确率应用预报模型集和消空因子集可进行有无区域性暴雨的逐日预报判别,其判别方程为:
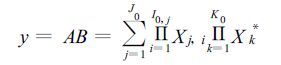
|
(3) |
这里,I0,j为第j号预报模型中的因子数; j为预报模型号; J0为当月预报模型数; Xj,i为第j号预报模型的第i号因子xj,i的布尔数 (二值化值); xj,i ∈[取值]时,取xj,i=1,反之xj,i=0;Xk*为第k号消空因子xk*的布尔数,xk* ∈ [取值]时,Xk*取值为0,反之取值为1;K0为当月消空因子数,A为预报模型集,B为消空因子集,y为判别值,当A≥1且B≥1时,Y=A ×B≥1,预报20:00~20:00有区域暴雨; 当A=0或B=0时,Y=A×B=0,预报无区域暴雨。
取式 (3) 中“ A”项≥1(即至少有1个预报模型套上) 的个例作为评定对象,5、6月判别方程的历史准确率见表 2。
|
|
表 2 5、6月判别方程的历史准确率 |
5 预报模型的检验效果与分析 5.1 判别方程的两年检验效果
利用研究中设计的预报判别方程实时自动化运行系统,以2000~2001年的5~6月实时的TTAA 08:00报文资料进行逐日套用,预报准确率见表 3。
|
|
表 3 判别方程在2000~2001年5~6月的检验准确率 |
5.2 检验结果的分析 5.2.1 2001年6月24日漏报原因分析
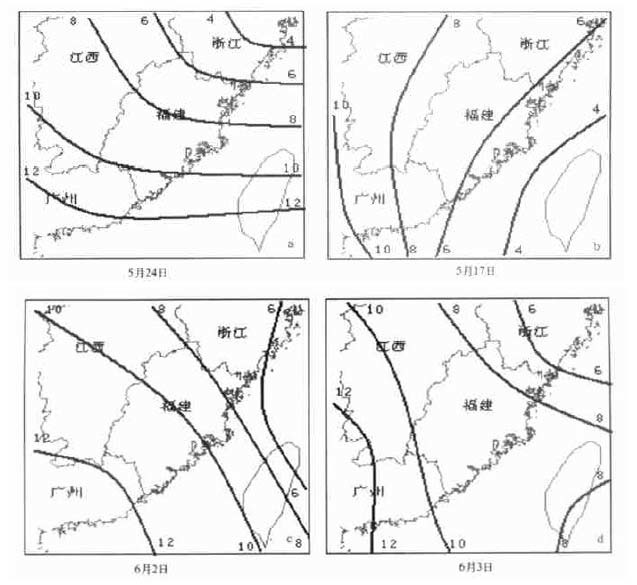
从2001年6月24日因子的输出值可见,预报模型6的“状态”最高,其3个因子的取值为:
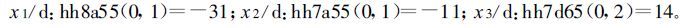
|
由6月预报模型6各因子的取值区间可知,x2、x3的编码值已为“1”,而x1的取值很接近其取值区间。这表明漏报很可能是由于x1取值区间的历史限定过严导致的。
将x1取值区间由原来的[-50,-35]放宽为[-50,-30],再对模型6重新做历史检验,结果仅增加了两次各有两站暴雨的空报,模型的准确率仍然可达11/13(0.85,原准确率为11/11),而且这两次空报均可纳入该月消空因子的消空行列之中。这表明这次漏报实际上是可以避免的,这同时也表明,通过实际应用,对预报模型进行完善与提高是必要的。
5.2.2 预报模型的预报效果稳定性分析由表 2和表 3可见,5月预报模型的实用准确率为0.786,比历史套用准确率0.839仅下降5.3 %,并保持无漏报; 6月预报模型的实用准确率为0.792,比历史准确率0.867下降7.5 %,若补回“可以避免的”唯一的一次漏报,则仅下降3.4 %,准确率仍可达0.833,而且两月的消空因子均保持无错消的记录。这表明预报模型及消空因子的延用效果都是比较稳定的。这可能与预报模型及消空因子的物理意义明确、合理有关。
图 2给出的是相应的预报模型的三层平均高度场。从中可见,预报模型的因子构成虽很简单,但却能清晰地体现出低层 (低) 涡、中层 (切变) 线、高层 (低) 槽的天气系统及其合理的垂直配置图像,而这正是人们所熟知的有利暴雨发生的形势模型。
|
|
| 图 2. 6月预报模型-12预报日3层平均高度场 (13个个例) (a)500 hPa,(b)700 hPa,(c)850 hPa | |
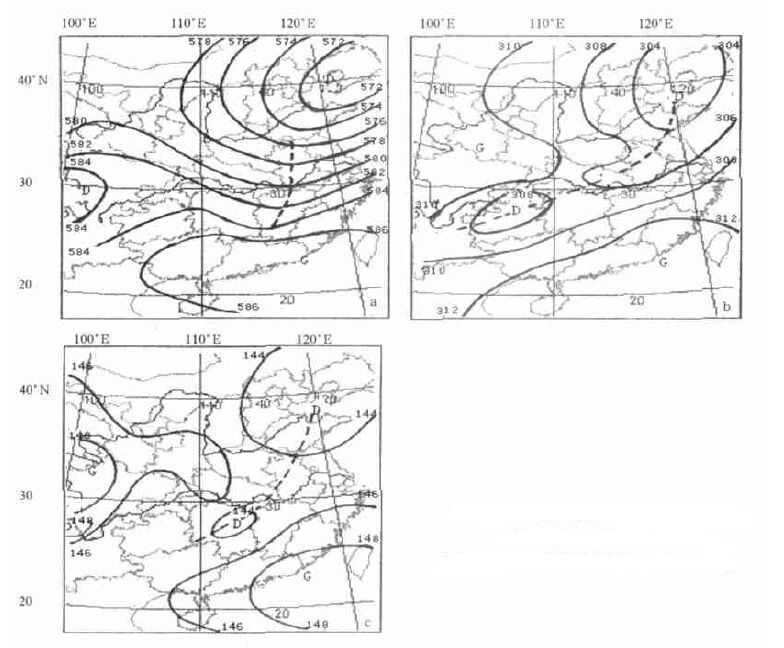
图 3给出的是相应的消空因子的3层平均高度场。从中可见,其形势特征与图 2截然不同,体现的是不利暴雨发生的形势模型。
|
|
| 图 3. 6月消空因子hh8b44(1,0)≥70的17个个例的3层平均高度场 (a)500 hPa,(b)700 hPa,(c)850 hPa | |
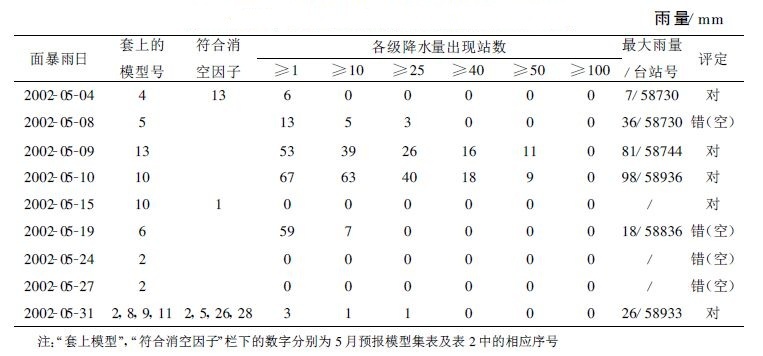
6 2002年业务运行情况与效果分析 6.1 2002年业务运行情况
预报模型于2002年5~6月投入业务使用,应用结果列在表 4、5、6中。表 7是福建省气象台短期科2002年5~6月17:00对外发布的暴雨警报的空、漏报情况,与其比较,模式的优越性在于没有漏报。这表明该预报模型在这个灾害性暴雨预报的焦点问题上,具有更高的可信度。但空报偏多。
|
|
表 4 2002年5月区域暴雨个例及其套用模式一览表 |
|
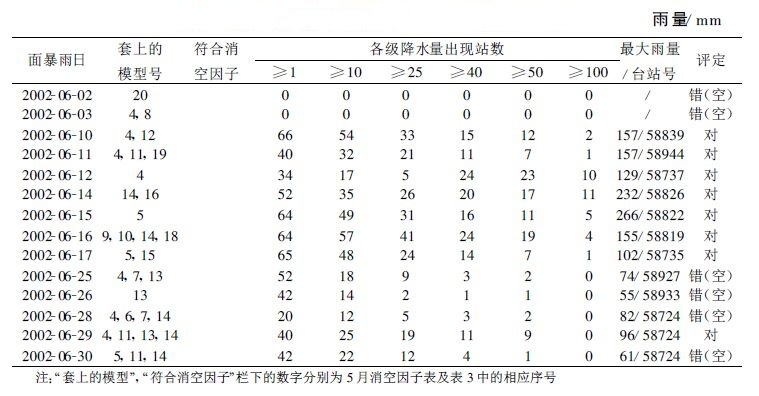
|
表 5 2002年6月区域暴雨个例及其套用模型一览表 |
|
|
表 6 判别方程在2002年5~6月的实用检验准确率 |
|
|
表 7 短期科2002年5~6月17:00暴雨预报准确率 |
6.2 空报原因分析
2002年入春以来,福建省气候异常,降水持续偏少,气温异常偏高,中南部大部县市出现严重春旱。与常年同期相比,5月大部地区降水偏少1~6成,6月上旬偏少达到6~10成。强降水主要集中在6月中旬。在此异常环流背景下,虽有天气系统影响,常因水汽条件不足,难以产生暴雨。
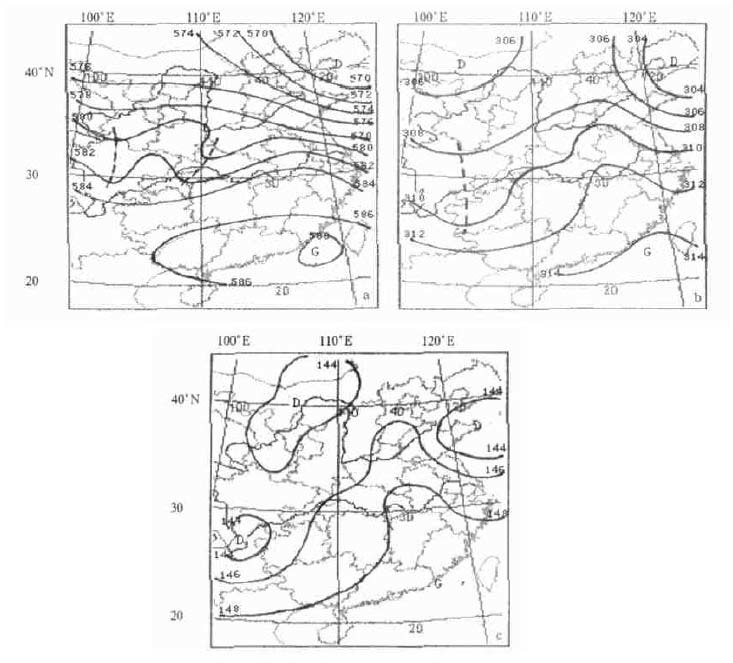
图 4是4次模式空报过程的T106的850 hPa比湿场,由图可见,福建均处在比湿低值区,比湿≤12 g/kg。根据福建前汛期大范围暴雨过程天气气候分析[7],大范围暴雨过程的850 hPa平均比湿场表现为有一≥14 g/kg的湿舌从华南沿海伸到福建。普查了2002年5~6月区域暴雨 (≥5站) 过程T106的850 hPa比湿场,均有>12 g/kg的湿舌从华南沿海伸到福建。显而易见,4次空报均因不具备水汽条件而致。可见,只要引进比湿场作为消空因子,将会大大减小空报率。
|
|
| 图 4. 4次空报时T106的850 hPa比湿场 (单位:g/ kg) | |
7 讨论与结论
研究结果表明,以高度场的滑动分区切比雪夫展开系数做为研制前汛期的区域性暴雨预报模型的信息源是合理且可行的,在天气预报研究应用上的良好作用是显然的:
(1) 低阶展开系数具有明确的天气学意义,可作物理解释,利于对预报模型的合理性进行识别。
(2) 滑动分区展开技术可对场信息做极限化的开发,能产生多种尺度的特征信息,既丰富了信息来源,又提高了信息质量,可为预报研究提供更为完备的信息环境,从而可获得对预报目标成因的更为完备的认识。
(3) 由于切比雪夫展开特征场是不随时间变化的,因而使基于历史资料的和基于实时资料的展开系数之间具有可比性。这意味着同一展开系数因子,将具有同一的物理内涵与作用。这就有利于增强预报模型延续应用的稳定性。
(4) 鉴于展开系数对天气形势特征具有很强的揭示能力,因此可以此来作为形势特征相似分析的依据,并由此制作暴雨的落区预报。本研究就是以此来解决暴雨的落区预报问题的,效果甚佳。
(5) 模型的不足之处是缺少直接表征水汽的因子,引进比湿场作为消空因子,将会大大减小空报率。可见,模型尚具有较大的优化空间。
| [1] | 陶诗言. 中国之暴雨. 北京: 科学出版社, 1980: 25-29. |
| [2] | 中国科学院大气物理研究所编. 切比雪夫多项式及其在气象水文中的应用文集. 沈阳: 辽宁科学技术出版社, 1987: 1-26. |
| [3] | 张明席. 切比雪夫展开系数时间变量的意义与应用.大气科学文集. 北京: 科学出版社, 1990: 235-242. |
| [4] | 张明席. 切比雪夫多项式化整计算的通用算法.大气科学文集. 北京: 科学出版社, 1990: 243-250. |
| [5] | 黄永玉, 朱应珍. 切比雪夫多项式约简算法的研究. 气象, 2000, 26, (1): 24–29. |
| [6] | 张明席, 朱应珍. Y为二值X为多级的相关量度研究. 自然科学学报, 1998, 1, (1): 5–9. |
| [7] | 林毅. 福建省前汛期大范围暴雨过程天气气候分析. 福建气象, 1997, (1): 21–25. |
 2003, 14 (4): 419-429
2003, 14 (4): 419-429