其中,水汽吸收区与窗区两个通道的反射率之比r可以从卫星测值中求出;在探空站所在的地方,沿光路的水汽总含量m为己知量,可以用统计方法求出系数A和B;在没有探空站的地方,可以根据系数A和B,用反演关系式求m。影响系数A的因素主要是大气的温、压、湿廓线和仪器的通道响应函数,影响系数B的因素是地表反射率。由于这些对反演关系式中的系数取值有影响的因素随时间和地点有变化,对不同地区和时段的探空站分别进行统计,得到不同的系数进行反演,取得了较好的效果。另外,还用质量控制手段控制了定位误差可能带来的影响。独立样本真实性检验表明,反演值和探空测值之间的偏差约为15%~20%,相关系数在90%以上。
其中,水汽吸收区与窗区两个通道的反射率之比r可以从卫星测值中求出;在探空站所在的地方,沿光路的水汽总含量m为己知量,可以用统计方法求出系数A和B;在没有探空站的地方,可以根据系数A和B,用反演关系式求m。影响系数A的因素主要是大气的温、压、湿廓线和仪器的通道响应函数,影响系数B的因素是地表反射率。由于这些对反演关系式中的系数取值有影响的因素随时间和地点有变化,对不同地区和时段的探空站分别进行统计,得到不同的系数进行反演,取得了较好的效果。另外,还用质量控制手段控制了定位误差可能带来的影响。独立样本真实性检验表明,反演值和探空测值之间的偏差约为15%~20%,相关系数在90%以上。
 In the formula, r, the ratio of observation values between the water absorption channel and the window channel, is known. At the locations around radiosonde stations, the total water vapor amount along the observation path is also known. Coefficients A and B can be derived by means of the statistic method. At other locations far from radio sonde stations, m is calculated with coefficients A and B. Factors affecting A are the atmospheric profiles of temperature, pressure and humidity and the channel response function of the imaging spectrometer. The factor affecting B is the surface reflectance. These factors are time-and location-related. Statistic calculation is performed respectively at different time periods and locations. The possible errors that otherwise may be introduced from the incorrect navigation of the images are limited by the quality control measure. Reality examination with independent radiosonde samples shows that the bias is about 15% to 20%, and the correlation coeffecient is above 90%.
In the formula, r, the ratio of observation values between the water absorption channel and the window channel, is known. At the locations around radiosonde stations, the total water vapor amount along the observation path is also known. Coefficients A and B can be derived by means of the statistic method. At other locations far from radio sonde stations, m is calculated with coefficients A and B. Factors affecting A are the atmospheric profiles of temperature, pressure and humidity and the channel response function of the imaging spectrometer. The factor affecting B is the surface reflectance. These factors are time-and location-related. Statistic calculation is performed respectively at different time periods and locations. The possible errors that otherwise may be introduced from the incorrect navigation of the images are limited by the quality control measure. Reality examination with independent radiosonde samples shows that the bias is about 15% to 20%, and the correlation coeffecient is above 90%.
水汽是地球大气的一种微量成分。其含量随时间和空间变率很大。水汽体积混合比的变化范围一般在0 %~4 %之间,最大可达7 %[1]。水汽在红外区的某些波段对辐射有强烈的吸收,通过吸收,水汽使地面射出辐射不能逸出到外空,而是贮存在大气层。所以,水汽是一种重要的温室气体。在大气的温度变化范围内,水汽是唯一可以发生相变的成分。随着大气温度、压力的变化,水汽的相态可以发生变化,生成雨、雪、云、雾等天气现象,同时向大气释放热量; 云、雾消散时,又从大气吸收热量。通过这样的热力过程,水的相变影响着大气的运动。大气中以不同相态存在的水与辐射之间,还存在着更复杂的相互作用。一旦水汽凝结成云,大气的辐射性质立即发生变化。不同性质的云,其辐射性质差异很大。水汽特有的这些物理性质,它对大气热力、动力过程的影响,它对形成天气现象的作用,以及它特别大的时空分布变率,使监测水汽的工作在天气和气候研究中占有重要的位置[2]。
大气中的水汽绝大部分位于对流层最底部的边界层,大气中水汽的总含量基本上是由边界层中水汽的含量决定的。因此,边界层水汽的监测是水汽分布监测的重点。然而,其中含有大气中大部分水汽的边界层,其温度与下垫面相差不大。从地物射出的热辐射,被边界层中的水汽吸收和再发射以后,其份额的改变也不会大。这就使得无论边界层中水汽的含量多还是少,从地物射出的热辐射在穿越边界层前后基本上保持不变。因此,用地物自身发射的红外热辐射,难以测量边界层中的水汽[3]。
R.Frouin等[4]首先提出,可以利用太阳反射光为辐射源,通过近红外区中一个弱吸收区、一个窗区两个通道,测量大气中水汽的总含量。这种方法利用太阳反射光作为辐射源,从而避免了在边界层里当介质与辐射源温度相同时无法测得水汽这个问题。R.Frouin等[4]还进行了飞机遥感实验,证实这种方法是可行的。黄意玢等曾计算过940 nm附近的水汽吸收对多个环境参数的敏感性,并且采用不同的通道组合作反演水汽总量的试验[5,6]。我国FY-1C星扫描辐射计己经设置了这样的观测通道。它的第2、第10通道的特征如表 1所示[7]。
|
|
表 1 FY-1C星扫描辐射计第2、第10通道的特征 |
从表 1可以看出,第2和第10通道都属于太阳反射光观测通道。其中第10通道在水汽的弱吸收区,第2通道在大气窗区。所以利用FY-1C的观测数据,可以实现R.Frouin等提出的大气低层水汽测量。
本项研究工作的目标是证实用FY-1C星第10通道与第2通道联合观测大气中水汽总含量的可行性,探索算法中存在的问题,提出解决的办法。
1 物理原理 1.1 用水汽吸收区与窗区反射率之比反演水汽总含量的方程在1 μm附近的近红外波段,从飞机或卫星上接收到的来自地物的辐射,主要是经过地气系统反射和散射的太阳辐射。在晴空陆地地区,由地表反射的直接太阳辐射,占该波段地物射出辐射的大部分; 除了被地表反射的太阳辐射以外,分子散射、气溶胶散射,以及这些散射辐射在地表、海表和大气内的多次反射和散射,也对地物射出辐射有贡献。我们把它们统称为程辐射,用LP表示。因此飞机或卫星上的传感器在某一波长λ所接收到的辐射可以表示为:
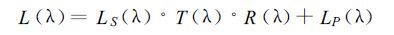
|
(1) |
其中LS是从大气外入射的太阳辐射,T(λ) 代表沿太阳—地表—传感器光路的大气透过率,R (λ) 为地表反射率。式中的第一项为地表反射项,第二项是程辐射。由于空气分子与气溶胶粒子和水汽一样,随着高度增加其密度迅速减少,所以程辐射主要来自低层大气,而且也受到水汽吸收的影响。即LP(λ) 本身就包含有大气中水汽含量的信息。
为了消除太阳对观测辐亮度谱分布的影响,同时将绝对测量问题变为相对测量问题,在可见光与近红外波段常采用叫做反照率的物理量描述地气系统的特征。它的定义为:
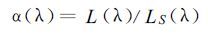
|
(2) |
由公式 (1) 和 (2) 得到:
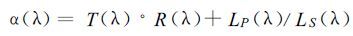
|
(3) |
在1 μm附近分子散射可以忽略。程辐射主要由气溶胶的散射辐射组成,其中包括一次散射和多次散射。在晴空,而且能见度较高 (如大于20 km) 的情况下,散射辐射又以一次散射的贡献为主。因此B.C.Gao等[8]假定:在气溶胶较少,如能见度大于20 km的情况下,在1 μm附近,程辐射可以认为与反射项成比例。若比例常数取为k,则式 (3) 变为
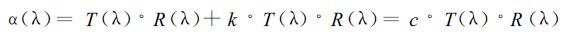
|
(4) |
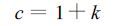
|
(5) |
在式 (4) 中,反照率α可以由观测得到,待求未知量 (水汽总含量) 包含在沿光路的大气透过率T(λ) 中。因此问题归结为两个:第一是如何求出式 (4) 中的另一个未知量地表反射率R(λ),从而可以求出T (λ); 第二是如何从T(λ) 中求出水汽总含量。
1.3 用水汽吸收区与窗区的反射率之比代替单个通道的反射率对于第一个问题,R.Frouin等[4]提出,虽然0.940 μm附近的地表反射率难以直接观测,但是可以在0.940 μm附近的窗区另外选一个观测通道,如0.865 μm或1.040 μm,将水汽吸收区与窗区两个通道的反射率相比较,求出其比率。这样就避免了对单个通道反射率作绝对测量的问题。水汽吸收区与窗区两个通道的反射率之比r表示为:
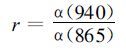
|
(6) |
将公式 (4) 代入公式 (6),可以得到:

|
(7) |
假定0.940 μm附近地表反射率随波长近似为线性变化:
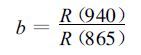
|
(8) |
则式 (7) 变为:
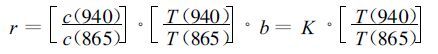
|
(9) |
式 (9) 中
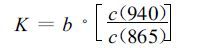
|
(10) |
K为比例系数。它计入了地表反射率的线性变化和气溶胶的消光。
假定0.865 μm通道的透过率为100 %,式 (10) 变为:
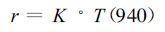
|
(11) |
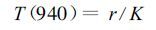
|
(12) |
r通过弱水汽吸收区和窗区两个通道测值的比求出。求准确的条件是对这两个通道进行高质量的相对定标。K是常数。所以第一个问题化为求两个通道上的地表反射率之比。
1.4 两个通道的反射率之比与水汽总含量的关系第二个问题是通过吸收带的透过率求水汽总含量。对于中等光谱分辨率的问题,较合适的透过率模式是Malkmus带模式[8]:
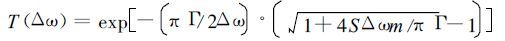
|
(13) |
式中Δω为光谱区间,Γ为谱线的平均半宽度,SΔω为谱线的平均线强,m为吸收成分含量。
从公式 (11)、(13) 式分析,水汽通道与窗区通道的反照率之比r随水汽吸收成分含量m变化的趋势大体是:r随m的平方根呈负指数变化。所以通道的反照率之比r可以表示为:
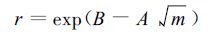
|
(14) |
式 (14) 中m为沿卫星观测光路的水汽含量。r可由卫星测值得到。用θS和θv分别表示获取r值那一时刻的太阳天顶角和卫星观测天顶角[8],当θS、θv不太大的时候 (如不大于60°),则垂直大气柱的水汽含量可近似表达为:
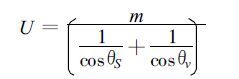
|
(15) |
所以只要求出m,垂直大气柱的水汽含量U可以用公式 (15) 推出。
1.5 以测站探空观测为辅助,用统计方法求大气中的水汽总含量用940 nm卫星观测值推算整层大气水汽含量的关键在于求出式 (14) 中的系数A和B。
A和B可以用统计方法求出。在探空站所在的地方,垂直大气柱的水汽含量U是已知量,用U可以求出沿卫星观测光路的水汽含量m。r当然也是已知量。用公式 (14),在探空站所在地方进行统计,可以求出系数A和B。最后用A和B两个系数作为己知量,又可以推算出图像上其它地方的水汽总含量U。
2 误差因素分析和为减少误差所采取的措施 2.1 传感器定标误差的影响仪器直接测量的是辐射能量值,然后利用辐射能量的比值导出水汽含量。因此,仪器的定标精度将影响反演水汽的精度。Y.J.Kaufman等认为,当仪器的定标精度为1 %或更好时,相应的水汽反演误差可以达到2 %~4 %[2]。但是,对于实际仪器而言,定标精度较高时也只能达到3 %~5 %。现在讨论定标系数的变化对反演结果的影响。定标公式写为:
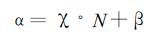
|
(16) |
式中N为观测计数值,定标得到的斜率为χ,截距为β。表 2为1999~2000年辐射校正场外定标的结果[9]。
|
|
表 2 1999~2000年辐射校正场外定标的结果[9] |
从表 2可以看出,FY-1C仪器的定标系数在一年之内发生了较大的变化。由式 (6) 可以求出每个观测像元水汽通道与窗区两个通道的反照率之比r为:
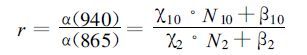
|
(17) |
公式 (17) 中变量的含义前面已经注解过,变量的下标为通道序号。式 (17) 中,χ10·N 10>>β10,χ2·N 2>>β2。因此,定标系数中的截距β对通道反射率之比r的影响是不大的。式 (17) 可以简写为:
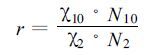
|
(18) |
为了考察定标系数的变化以及将定标公式简化对通道反射率之比计算结果的影响,我们将通道10和通道2的典型观测计数值150和202,分别用1999年7月7日和2000年9月20日的定标系数,以公式 (17) 和 (18) 代入,计算出这两个通道的典型反射率之比。计算结果列在表 3中。
|
|
表 3 水汽通道与窗区两个通道的典型反照率之比r的计算结果 |
从表 3中我们看到,无论用公式 (17) 还是用公式 (18) 进行计算,水汽吸收区与窗区两个通道典型反照率之比的计算结果都有很好的时间连续性。再来考察表 2,从1999年7月7日到2000年9月20日定标系数已经发生了很大的变化。但是1999年7月7日χ10/ χ2=0.988,2000年9月20日χ10/ χ2=0.981,两者相当一致。另外,用简化公式 (18) 与全公式 (17) 算出的通道反照率之比的差别大约为百分之二。以上事实说明:两个通道间的相对定标变化不大,它们的通道反射率之比也就变化很小,简化公式 (18) 也是可以用的。
2.2 温、压、湿廓线,云和气溶胶的影响由于吸收带的形状依赖于温度,所以同样多的水汽处于不同温度时,吸收辐射的量是不同的。B.C.Gao等预计由于大气温、压、湿廓线不准确带来的误差不超过5 %[3]。Lorentz加宽依赖于气压,大气压随高度增加单调下降,因此仪器视场内的地面气压或高程可以影响反演精度。
大部分水汽处于云层以下,有云层存在时,云下的反射辐射被云遮挡,在计算模型中没有计入,致使估算的水汽含量偏低。Y.J.Kaufman等认为由此造成的误差与图像内的云量有关[2]。另外,云区所在像元下垫面的反射率偏离地表反射率,对计算结果也有影响。
在气溶胶较少,如能见度大于20 km的情况下,可以认为在1 μm附近程辐射项与反射项成比例。这是用通道反射率之比反演水汽总含量的基本假定。但是,在气溶胶很多时这个假定不成立。这也是误差来源之一。
考虑到以上可能带来误差的因素,为了减少误差,本项研究工作取2000年6~7月这一特定季节的探空及卫星资料作为样本,按区域对样本分别统计系数A和B,以消除由于在不同地点,大气廓线差别较大带来的误差,这样做也可以消除地表反射率随地点不同引起的误差。
由于近红外通道对于云而言是不透明的,所以必须进行云检测,利用第4第5红外通道计算地面亮温,将它与该日期的地面温度观测报告做比较,亮温高于地面气温视为无云。
为了在反演中避免气溶胶的影响,用同时间同地点地面报表资料中的能见度观测作为气溶胶含量的一个指标。当能见度小于20 km时,这一天的样本不参与统计。
2.3 定位误差的影响如引言中所述,大气中水汽含量的空间变化率是很大的,所以如果卫星资料的定位精度不高,探空资料与卫星资料在空间上不匹配,就可能造成较大的计算误差。为了抑制定位不准所造成的误差,在数据处理中采用了对像元求平均的算法。取探空站所在地点周围15 ×15像元的区域内对图像进行平均处理; 以3个像元为步长,将15 ×15像元组成的区域分为25个子区域,对每个子区域求平均,分别反演水汽总含量。然后对25个子区域反演出的水汽总含量求标准差。若标准差大于某一阈值,则意味着此地水汽总含量的空间梯度很大。在这个地方,定位的偏差可能会造成较大的影响,这个探空站的数据不参与系数A和B的统计。下面以敦煌站为例,说明采取这个措施以后的计算结果。
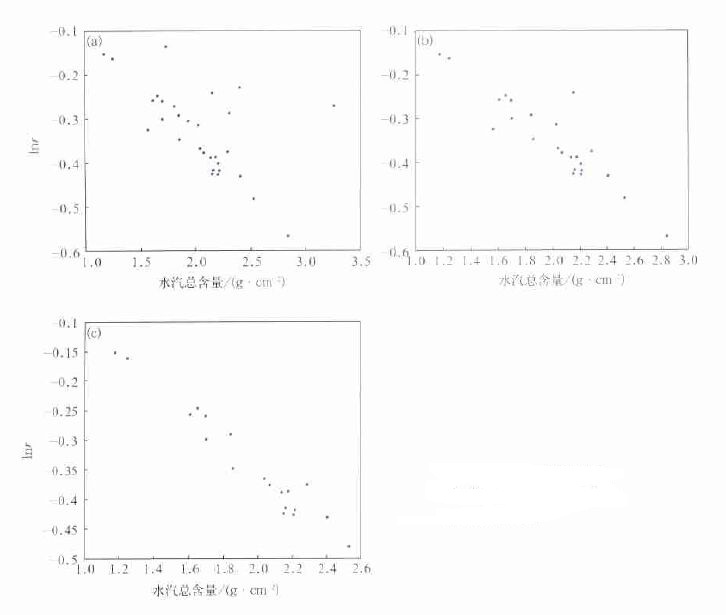
图 1是站号为52418敦煌站的统计结果。在图 1中,纵坐标为通道反射率之比r的自然对数值,横坐标为沿整个光路的水汽总含量。图 1a、b、c的区别就是所取的标准差门槛值不同。所得统计结果的相关系数也不同。标准差门槛值越严格,统计结果的相关系数越高。图 1a标准差门槛最大 (最不严格) 为0.1,统计结果的相关系数为60 %; 图 1b标准差门槛为0.05,统计结果的相关系数为91 %; 图 1c标准差门槛最小 (最严格) 为0.04,统计结果的相关系数为97 %。敦煌站的统计结果表明,采用区域标准差,可以有效地过滤掉水汽总含量空间梯度大时,定位不准可能带来的计算误差。
|
|
| 图 1. 敦煌站的系数统计结果 (a),(b),(c) 标准差门槛分别为0.1, 0.05, 0.04 | |
2.4 地表反射率的影响
将公式 (7) 与 (14) 联立,得:
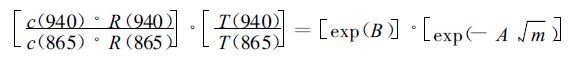
|
(19) |
式 (19) 等号的左右两端都是乘式。其中乘数


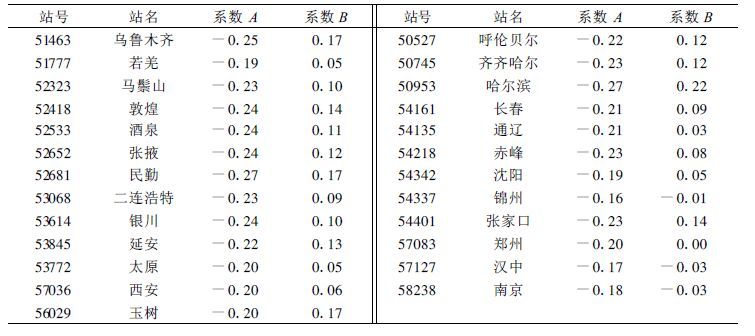
我国地形复杂多样,各地区的地表反射率有很大差异,地表反射率随季节变化也很大。如果把不同地区、不同季节的数据放在一起统计,对整幅图像都采用相同的系数进行水汽总含量反演,可能会造成较大偏差。表 4是对个别探空站分别统计所得的水汽总量反演系数A和B。
|
|
表 4 个别探空站分别统计所得的水汽总量反演系数A和B |
从表 4中对个别探空站分别统计所得的系数来看,斜率A的可变性并不很大,最大值为0.27,最小值为0.16。而截距B的可变性相当大,最大值为0.22,最小值为-0.03。本节中前面的分析己经指出,截距B与地表反射率关系密切。因为长江以南地区经常有云覆盖,有效样本很少,以上的分析主要依据东北、华北、西北地区的站点得出。
为了尽可能减少把地表反射率有很大差异的样本放在一起统计对计算结果的影响,我们把探空资料样本划分为几个不同的区域和时段,分别对通道反射率之比以及沿整个光路的水汽总含量两个物理量作统计回归,求出不同区域和不同时段的系数A和B。根据各地区的地理情况并参照以上个别探空站点的统计结果,自北向南分成5块:
① 33°~43°N、100°~115°E:该区域北边是内蒙古高原西部,海拔在1000~2000m,地表起伏和缓多为戈壁和沙漠,如腾格里沙漠,毛乌素沙地都在此区域内,西边是青藏高原的东端,东边是吕梁山与太行山,南边有岷山、秦岭和大巴山,中间是黄土高原。
② 40°~50°N、110°~120°E:是内蒙古高原东部。东边是大兴安岭,森林茂密,西部是广阔的草原。海拔在1000m上下,地势起伏和缓。
③ 40°~50°N、120°~130°E:该区域的西边是大兴安岭,东边是小兴安岭和长白山,都是我国重要的林区,中间地带有嫩江、松花江与辽河,形成土壤肥沃的东北平原。
④ 33°~40°N、115°~120°E:该地区大约处于长城以南、淮河以北、西起太行山一线、东至黄、淮河入海口和山东半岛。
⑤ 30°~33°N、105°~112°E:该地区处于淮河与长江之间。北边是大巴山,南边是川东北的丘陵,东边有武当山和巫山,西部是四川盆地的东北部。
对2000年6~7月每个区所有的样本进行了回归分析,求出逐区回归系数如表 5所列:
|
|
表 5 2000年6~7月分区统计所得的水汽总量反演回归系数A和B |
3 独立样本真实性检验 3.1 偏差
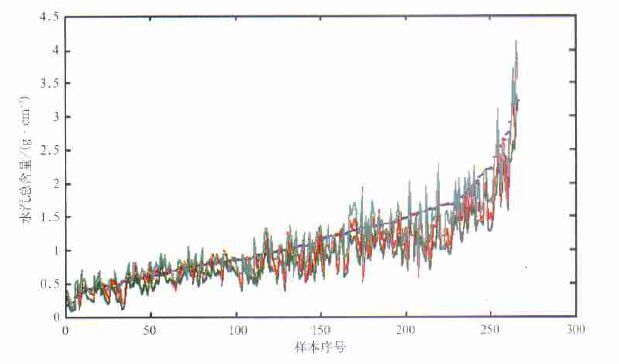
用2001年5月20日至30日的卫星和探空观测资料对反演结果进行了独立样本检验,图 2是独立样本真实性检验所得反演结果偏差。在图 2中,纵坐标为整层水汽总含量,横坐标为观测样本序号。观测样本依用探空资料算出的水汽总含量为排序的依据,即靠近图左侧的样本探空测得的水汽总含量较低,靠近右侧较高。图 2中有4条曲线:其中自左向右单调上升的曲线为探空测得的水汽值; 蓝色曲线为使用单个探空站点的资料计算出的系数反演所得的水汽值,其偏差为16 %; 红色曲线为使用分区资料计算出的系数反演所得的水汽值,偏差为17 %; 绿色曲线为使用全国统一资料计算出的系数反演所得的水汽值,其偏差为22 %。由图 2可见,由于全国各地的天气情况与地表状况差别很大,全国使用同一系数反演所造成的偏差较大。用分区系数使反演结果有了改进。但使用单个探空站点的资料计算出的系数与使用分区系数反演出的结果大致相当。这说明,在同一地区内使用几个站点作为样本,已经大致可以代表本区的大气与地表状况,此时反演偏差的主要来源已经不再是大气或地表状态的差别。
|
|
| 图 2. 独立样本真实性检验所得反演结果偏差 | |
3.2 相关
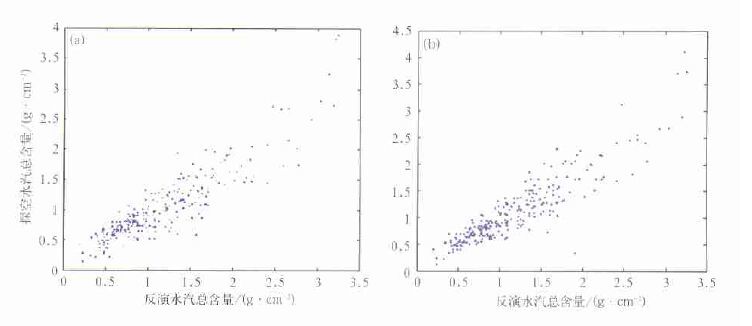
用同一组独立样本做了相关性检验。图 3是独立样本真实性检验所得反演结果与实况之间的相关系数。图 3中纵坐标为探空测得的水汽总含量,横坐标为反演所得的水汽总含量。图 3a中的反演水汽值是用分区系数算出的,相关系数为0.9013;图 3b中的反演水汽值是用单站系数算出的,相关系数为0.9164。
|
|
| 图 3. 独立样本真实性检验所得反演结果与实况之间的相关系数 (a),(b)分别为分区系数和单站系数计算结果 | |
3.3 反演水汽的水平分布
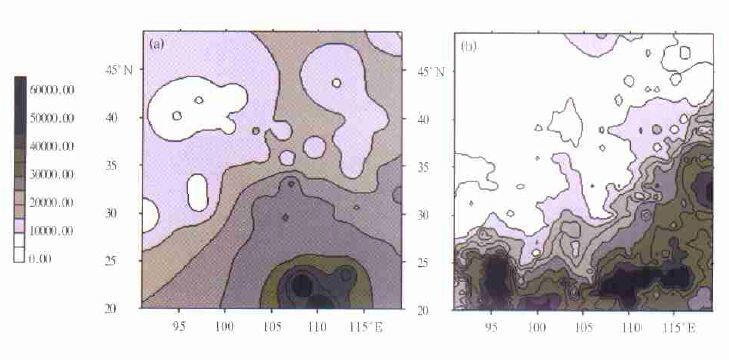
图 4a、b分别为用2001年5月13日的探空资料算出的水汽实况 (作为真值) 与反演值。从图 4中可以看出,真值与反演值两张图的大体形势是一致的,相应的高值区和低值区也能对应。而图 4b比图 4a显示出水汽总含量分布的更多细节。例如,在图 4b左下角有一个高值区,这个高值区在图 4a中没有。高值区位于喜马拉雅山南麓的平原地区,那里是地球上年降水量最多的地区之一,但是没有探空资料,我们认为反演图更加合理。
|
|
| 图 4. 用2001-05-13的探空资料算出的水汽总含量(a)和用FY-1C资料反演出的水汽总含量(b) | |
4 结论
本文利用FY-1C资料具体实现了用太阳反射光通道遥测大气中水汽的总含量的算法,并用独立样本与探空资料进行了比对,检验了反演结果。得出的主要结论如下:
(1) 用FY-1C资料中近红外水汽吸收区和窗区两个通道测值,可以反演出大气水汽总含量。反演关系式为
(2) 影响系数A的因素主要有大气温、压、湿廓线和仪器的通道响应函数,影响系数B的因素是地表反射率。
(3) 由于这些对反演关系式中的系数取值有影响的因素随时间和地点有变化,所以针对特定的地区和时段分别进行统计,采用不同的系数进行反演,取得了较好的效果。
(4) 用质量控制手段控制了定位误差可能带来的影响。
(5) 独立样本检验表明,反演值和探空测值之间的偏差约为15 %~20 %,相关系数在90 %以上。
| [1] | 许绍祖. 大气物理学基础. 北京: 气象出版社, 1993: 18. |
| [2] | Kaufman Y J, Gao B C, Remote sensing of water vapor in the near-IR from EOS-MODIS.IEEE Trans.Geosci. Remote Sensing, 1992, 30, (5): 871–884. DOI:10.1109/36.175321 |
| [3] | Weldon R B, Holms S T.Water vapor imagery interpretation and applications to weather analysis and forecasting.NOAA Technical Report NESDIS No.57, 1991. |
| [4] | Frouin R, Deschamps P Y, Lecomte P, Determination theory and airborne verification. J.App l.Meteor, 1990, 29, (6): 448–460. DOI:10.1175/1520-0450(1990)029<0448:DFSOAT>2.0.CO;2 |
| [5] | 黄意玢, 董超华, 刘志权, 等. 940 nm水汽通道反射率计算. 应用气象学报, 2002, 13, (4): 413–421. |
| [6] | 黄意玢, 董超华. 940 nm通道遥感水汽总量的可行性试验. 应用气象学报, 2002, 13, (2): 184–192. |
| [7] | 董超华, 章国材, 邢福源, 等. 气象卫星业务产品释用手册. 北京: 气象出版社, 1999: 218. |
| [8] | Gao B C, Goetz A F H, Column atmospheric water vapor and vegetation liquid water retrievals from airborne imaging spectrometer data. J.Geophys.Res, 1990, 95, (D4): 3549–3564. DOI:10.1029/JD095iD04p03549 |
| [9] | 张玉香, 胡秀清, 戎志国, 等. FY-1C和FY-2B卫星遥感器可见光通道在轨辐射定标.中国遥感卫星辐射校正场2000年敦煌青海湖场地综合试验成果文献. 北京: 国家卫星气象中心, 2001: 133. |
 2003, 14 (4): 385-394
2003, 14 (4): 385-394