2. 北京大学物理学院大气科学系, 北京 100871
2. Department of Geophysics, Pek ing University, Beijing 100871
在湍流大气中成像理论的研究中, Fried[1]提出了大气相干长度r0的概念, r0的物理意义是在达到理论衍射极限条件下, 所能使用的光学仪器孔径的上限[1, 2]。Roddier[3]给出了r0与折射率结构系数Cn2沿光路积分间的关系。当今, 在诸如航空、航天器的测量、跟踪与控制以及天文观测的实施过程中, r0都是需要了解的一个基本参量。得到r0的最好方法是直接或间接测量[4, 5, 6], 但由于人力物力所限, 这种测量很难在大范围内长时间地进行。为了了解r0在全国范围内的时空分布, 在Tatarski[7]理论模式的框架下, 利用常规气象探空资料从理论上计算Cn2[8, 9], 进而得到r0不失为一种可取方法。本文用这种理论计算方法, 计算了我国地面81个探空站地面上空的r0, 并讨论了其地理分布与季节变化。
1 理论模型, 计算方法与资料来源在满足局地均匀各向同性湍流条件下, 在惯性子区间内, 大气折射率n可以看作为保守被动混合场, 其随机扰动特征可用折射率n的二阶矩———结构函数Dn表述。r在湍流内尺度与外尺度之间时, Dn满足2/3定律[7], 即
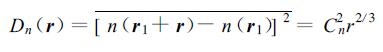
|
(1) |
对可见光波段, 大气湿度对折射率的作用可以略去。在空气受到扰动时, 可看作沿干绝热路径运动的假定下, 位温θ为保守被动混合场, 折射率亦可用具有保守属性的位温来表示。折射率结构系数Cn2可表示为[7, 10]
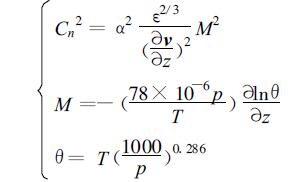
|
(2) |
其中α为数值常数, ε为单位质量流体湍能耗散率[7, 8, 9], p为压力, T为温度, v为水平风速, θ为位温。
相干长度Fried参数r0可表示为[3]
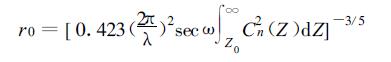
|
(3) |
λ为观测波长, ω为天顶距, Z0为大气底层高度。
ε为高度的函数。Hufnagel[9]综合实验结果所得到的拟合曲线, 由温景嵩给出此拟合曲线的内差公式[8]。Tatarski[7]通过观测近地面大气层温度结构函数得到α=2.4。但在此工作中, 对近地面出现逆温的稳定层结时, α显著变小, 而且发生缓慢变化, 平均α≈0.37。温景嵩[8]通过上海天文台佘山站星光抖动角与天顶距的关系及上海气象台探空资料的平均场得到20 m以上大气层的α=0.217。Colman等[10]在研究大气湍流外尺度时使用的α=1.67。我们用云南天文台在丽江高美古[7]以及安徽光机所[6]在北京天文台兴隆站实测所得的r0的27个样本, 与相应的丽江气象台和北京气象台的常规气象探空数据, 统计得到α=0.3532[11-15]。在得到这个α数值的过程中, 我们将式 (3) 变形为
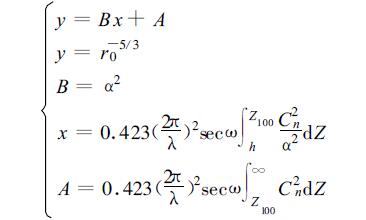
|
(4) |
其中Z100为100 hPa高度, 在假定Z100~100 hPa高度以上Cn2积分为常量的条件下, 得到线性回归方程为
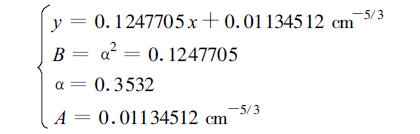
|
(5) |
其统计置信度通过1 ‰检验。
本文由式 (5) 出发, 取波长λ=0.55 ×10-6m, 天顶距ω=0, Z0=h为各站海拔高度, 用各站常规气象探空数据计算x, 得到y, 最终得到各站各次探空数据所对应的地面r0。
气象探空数据取自中国气象局气候资料中心所提供的数据光盘, 包括1986~1995年10年间08 :00(北京时, 下同) 和20 :00逐日逐次探空数据, 其中71个站包括10年数据, 10个站包括1~5年数据。本文所采集的数据量近5 ×107个。
2 计算结果与统计分析对各测站逐日12 :00(UTC) 的探空数据, 由式 (4)、(5) 计算出各自的r0, 进而统计得到多年年平均值及逐月平均值。
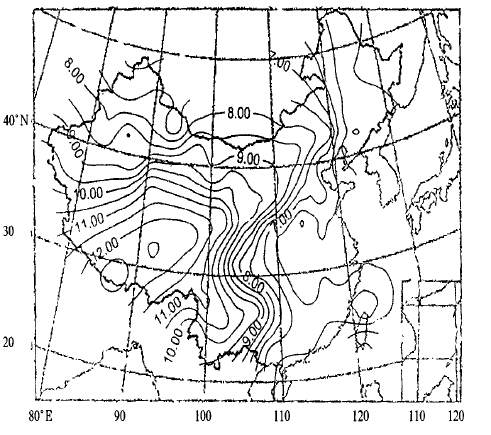
图 1给出12 :00(UTC) 的r0多年年平均值的地理分布, 由图 1可以看出世界时12 :00 r0的高值中心处于西藏定日 (12.87 cm)、黑河 (12.65 cm) 一带。其高值脊沿两个方向延伸, 一个由青藏高原伸向东北方经黄土高原至蒙古高原; 另一个由青藏高原伸向东南方经云贵高原东伸至江南丘陵。低值中心在武汉至郑州一带, 其低值槽向西伸向四川盆地。将上述r0的地理分布与我国地形图对比可以看出, r0的分布与地形分布基本一致, 即海拔高的地方r0大, 反之亦然。但也不尽如此, 如伸向蒙古高原的高值脊, 有一支向南伸至黄淮海平原。从在此脊内外相邻的两个测站—徐州 (海拔42 m, r0=6.58 cm), 郑州 (海拔111 m, r0=5.89 cm) 的数据可知, 郑州海拔高于徐州69 m, 但r0却低0.69cm。可见, 虽然地形基本上决定了地面r0的分布趋势, 但大气光学湍流结构的差异在海拔高度相近的条件下, 对地面r0分布起了关键的调制作用。
|
|
| 图 1. 12:00(UTC) r0多年年平均分布 (单位:cm, 下同) | |
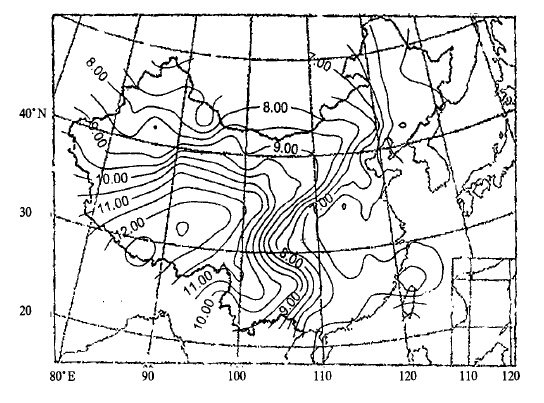
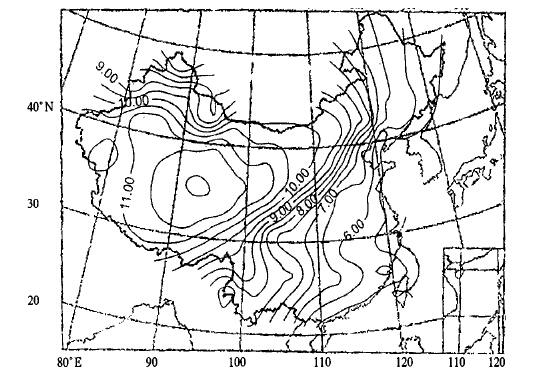
图 2和图 3分别给出了1月和7月12 :00(U TC) 的r0的月平均分布。由这两个图可以看出, r0分布的基本走势与图 1给出的r0年平均分布基本上一致。1月r0的高值中心区在西藏的定日 (海拔4301 m, r0=13.37 cm)、拉萨 (海拔3650 m, r0=13.06 cm) 一带; 7月r0的高值中心区在青海的格尔木 (海拔2809 m, r0=11.97 cm)、芒崖 (海拔3138m, r0=11.83 cm) 一带。r0的高值中心在7月较1月明显北移。7月海拔较高的定日及拉萨r0分别为10.96 cm及11.21 cm, 低于河西走廊的敦煌 (海拔1140 m, r0=11.41 cm)。1月r0低值中心在西安 (5.18 cm) 附近, 7月低值中心不甚明显, 但伸向四川盆地的低值槽依然可见。r0高值中心区在7月对1月而言明显北移了5°左右。从全年12个月r0的月平均值逐月分布可知, r0高值中心区自6月有一个明显的北移, 且维持到9月, 均在35°N左右, 而其它月份均在30°N左右。
|
|
| 图 2. 12 :00(UTC)1月r0月平均分布 | |
|
|
| 图 3. 12 :00(UTC)7月r0月平均分布 | |
3 讨论
(1) 上述高值中心区的季节性变化, 特别是6~9月高值中心明显地偏离了海拔高度的高值中心的现象与副热带急流在我国西部相应的月平均位置变化相一致[16]。副热带急流所处位置所对应的大尺度大气层结结构可能不利于光学湍流的发展[17]。
(2) 本文采用的计算模式 (5) 中A=0.01135 cm-5/3, 代表测站100 hPa高度以上大气光学湍流对r0的贡献为常量。它所对应的各测站的r0最大值均为14.69 cm, 这是本模式的一个局限性。当r0非常高而优于此值时, 本模式低估了r0的值。
(3) 由于常规气象探空数据取自气球探空仪的测量结果, 它只代表了一个测站附近、1小时左右的大气平均状态。所以由模式 (5) 所计算出的r0也只能代表测站附近区域1小时左右r0的平均结果。另外受常规气象探空仪探测精度的限制, 往往漏掉某些大气层结的精细结构, 而有时这种精细结构对r0的影响是十分重要的[18], 从而高估了r0的值。
| [1] | Fried D L, Optical resolution through a randomly inhomegeneous medium for very long and very short exposures. J.Opt.Soc.Am., 1966, 56, (10): 1372. DOI:10.1364/JOSA.56.001372 |
| [2] | 仇朴章, 刘忠. 现代天文选址中的视宁度. 天文学进展, 1993, 11, (1): 55. |
| [3] | Roddier F, The effects of atmospheric turbulence in optical astronomy. Prog.Opt, 1981, 19: 281. DOI:10.1016/S0079-6638(08)70204-X |
| [4] | Coulman C E, Fundmental and applied aspects of astronomical " seeing". Ann.Rev.Astron.Astrophys, 1985, 23: 19. DOI:10.1146/annurev.aa.23.090185.000315 |
| [5] | 吴晓庆, 曾宗泳, 马成胜, 等. 兴隆大气湍流气球探测. 量子电子学报, 1996, 13, (4): 385. |
| [6] | 于建明, 刘子忠, 栾蒂, 等. 丽江高美古天文候选点的视宁度观测. 云南天文台台刊, 1996, (增刊): 48. |
| [7] | 塔塔尔斯基. 湍流大气中波的传播理论. 温景嵩, 宋正方, 曾宗泳, 等译. 北京: 科学出版社, 1978. |
| [8] | 温景嵩, 顾慰渝, 魏公毅, 等. 上海湍流强度分布的一个模型. 气象学报, 1980, 38, (2): 160. |
| [9] | Hufnagel R H, Stanley N R, Modulationt ransfer function associated with image transmission through turbulent media. J.Opt.Soc.Am., 1964, 54, (1): 52. DOI:10.1364/JOSA.54.000052 |
| [10] | Coulman C E, Vernin J, Coqueugniot Y, et al. Outer scale of turbulence appropriate to modeling ref ractive index structureprofiles. Appl.Opt, 1988, 27, (1): 155. DOI:10.1364/AO.27.000155 |
| [11] | 李建国, 毛节泰, 黄寅亮, 等. 在折射率结构系数Cn2计算中决定数值常数α的一种方法. 中国学术期刊文摘 (科技快报), 1999, 5, (9): 1172. |
| [12] | 李双喜, 付元芬, 黄寅亮, 等. 利用兴隆站所测的Fried参数r0确定湍流折射率结构系数Cn2中的数值常数α. 天津理工学院学报, 2000, 16, (1): 64. |
| [13] | 付元芬, 李双喜, 黄寅亮, 等. 折射率结构系数Cn2中的数值常数α. 中国学术期刊文摘 (科技快报), 2000, 6, (1): 129. |
| [14] | 李双喜, 付元芬, 黄寅亮, 等. 对折射率结构系数Cn2中的数值常数α的修正. 中国学术期刊文摘 (科技快报), 2001, 7, (1): 126. |
| [15] | 李双喜, 付元芬, 黄寅亮, 等. 对湍流折射率结构系数Cn2中的数值常数α的讨论. 中国学术期刊文摘 (科技快报), 2001, 7, (2): 225. |
| [16] | 盛承禹. 中国气候总论. 北京: 科学出版社, 1986. |
| [17] | 付元芬, 李双喜, 黄寅亮, 等. 我国对流层中层大气Fried参数r0的计算与统计分析. 中国学术期刊文摘 (科技快报), 2001, 7, (8): 1005. |
| [18] | Coulman C E, Vernin J, Fuchs A, Optical seeing-mechanism of thin turbulent laminae in the atmosphere. Appl.Opt., 1995, 34, (24): 5461. DOI:10.1364/AO.34.005461 |
 2003, 14 (2): 230-235
2003, 14 (2): 230-235

