2. 西安建筑科技大学市政与环境工程学院, 西安 710055
2. Department of City Apparatus and Environmental Engineering, Xi'an Architecture and Technology University, Xi'an 710055
国际上较早开展空气污染预报的国家有美国、英国、日本、荷兰、前苏联等[1, 2], 我国在这方面的研究工作虽然起步较晚, 但目前已不同程度地在全国大部分地区开展起来。到1997年年底, 全国先后有39个城市开始发布空气质量周报。在周报工作的基础上, 又有许多城市利用自动监测数据进行空气质量的日报工作[3]。2000年11月国家环保总局和中国气象局联合发文, 要求47个环境保护重点城市于2001年6月5日联合发布环境空气质量预报。可见我国的空气污染预报工作正蓬勃发展。
大气污染预报的主要方法有:潜势预报、统计预报和数值模式预报, 它们各有优缺点[4]。数值模式是空气污染预报的发展方向。在当前情况下, 根据国内各城市现有的资料, 资源状况应首先以统计预报为主, 此方法易于推广使用。但当前采用的某些统计方法, 在选择预报因子时均没有考虑气象因子之间的相关性, 挑选的气象因子由于其非正交, 使回归计算的结果不稳定, 给计算带来一定的误差。针对以上不足, 本文把一元线性回归分析、自然正交分解 (EOF) 和逐步回归方法结合起来, 得到一种新的预报方法, 并建立了变量之间相互独立的统计模型。
1 使用方法、资料及统计量本文的新方法是以一元线性回归分析、逐步回归方法[5]、自然正交函数分解 (EOF)[6]为基础, 通过经验正交函数展开, 不仅使原来的预报各因子各个自变量变为正交的量便于回归分析, 而且一般只要分析几个主要分量就能代替对全部分量的分析, 获得要素场空间和时间基本特征的信息。
预报流程为对预报因子与西安市采暖期和夏季SO2浓度进行一元线性回归分析, 在一定置信水平下, 选取线性显著性相关的预报因子, 把这些因子进行EOF分析, 消除因子间的相关性, 得到正交的主成分, 再在一定置信水平下, 输入到逐步回归运算中, 建立预报模型, 从而形成一种新的建模方式。通过去掉最前一天的资料, 加入新一天的资料, 模型的系数及自变量都在滚动变化, 使预报模型反映污染物的最新情况, 预报模型更真实可信。因此该预报模型还是一个变系数的模型。
本研究挑选了西安市站1995~1999年采暖期和夏季每日的地面气象资料 (如温度、风、气压等) 和二氧化硫浓度资料, 其中, 1999年作为独立资料来验证模型预报效果。根据西安市的气候及采暖情况, 采暖期时段定为前一年11月中旬到当年3月中旬。夏季为6月到9月。
在进行运算前, 各预报因子均进行标准化处理, 使之变成无量纲量。建立预报模型时, SO2浓度使用距平值。
为检验预报模型的效果使用了如下统计量:
误差缩减值 (Re)[7], 计算方法如下:
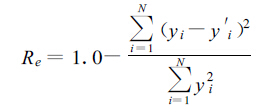
|
其中yi和y′i分别是观测值和估计值与非独立资料平均的偏差, 公式最后一项是估计量的误差平方总和与经验得到的回归方程估计之前的误差平方总和之比。
Re统计量可以从-∞到最大值1.0范围内, 1.0表示完全评价, 任何正的Re值表示回归模型具有一定的功能, 用该模型预报结果有一定的价值。它是精确检验所建方程可靠性的统计量, 比起别的检验统计量来, 它具有有效的诊断能力, 为一敏感的检验量。
相对误差 (%)=((预测值-实测值)/实测值)×100%。
预报的级别命中率 (%)=(预报值与实测值级别相同的天数/总天数)×100%。
2 统计预报模型的建立及结果分析 2.1 预报因子的选取城市空气中污染物的扩散、稀释和消除过程的快慢, 主要是由当地、当时的天气形势所决定, 影响污染物浓度的气象参数主要有风、大气稳定度、混合层高度和降水等。在此前提下, 结合天气预报经验, 粗略选取以下具有较明确物理意义的常规地面观测因子作为预报因子。
(1) 当日的日平均风速, 当日的08 :00, 14 :00, 20 :00(北京时, 下同) 风速。反映空气平流输送能力的强弱, 一般情况下, 风速大, 空气污染轻, 风速小, 空气污染就重。(2) 当日的日平均气温、前一日的日平均气温。反映城市所处冷暖气团状况。(3) 当日与前一日日平均气温之差。显示控制城市气团变化趋势, 间接反映气温稳定度状况。(4) 当日的日平均气压, 前一日的日平均气压。反映城市所处的气压场是低压还是高压。(5) 当日与前一日日平均气压之差。反映控制城市大气气压场的变化趋势。(6) 当日最低气温, 前一日最低气温, 当日最高气温, 前一日最高气温。反映城市逆温及混合层状况。(7) 当日降水量。反映天气状况及污染物的冲刷情况。(8) 当日辐射, 当日总云量。反映城市大气稳定度状况。(9) 当日的日照时数, 当日08 :00, 14 :00, 20 :00能见度。反映城市天气状况及污染状况。
另外, 由于空气污染物具有延续性, 污染物浓度由低到高有一个累积过程, 从高到低也有一个稀释过程, 如无特殊情况出现 (沙尘暴), 污染物浓度的变化是一个渐变过程, 因此把前一日的日均浓度当作一个预报因子来考虑。
2.2 预报模型的建立及结果分析 2.2.1 采暖期分别对上述所选预报因子与西安市采暖期SO2日均浓度进行一元线性回归分析, 在信度α=0.05下, 对因子进行筛选, 得到显著性线性相关的因子有:前一日日均浓度、前一日日均温度、当日日均温度、当日与前一日气压差、当日最高温度、当日最低温度、当日08 :00、14 :00、20 :00风速, 当日08 :00、14 :00、20 :00能见度, 当日日均风速。
14个预报因子与SO2浓度线性相关的合理性分析如下:采暖期天气形势变化较慢, 浓度延续性较大, 表现为前一日日均浓度与SO2浓度正相关; 采暖期温度高, 有利于大气扩散, 表现为前一日日均温度和当日日均温度与SO2浓度负相关; 当日与前一日气压差越大, 风速越大, 大气扩散越强烈, 有利于SO2扩散, 表现为与SO2浓度负相关; 当日最高温度、当日最低温度越高, 最大、最小混合层高度越高, 越有利于大气扩散, 表现为当日最高温度、当日最低温度与SO2浓度负相关; 风速越大, 越有利于大气扩散, 表现为08 :00、14 :00、20 :00风速、日均风速与SO2浓度负相关; 能见度越大 (小), 污染越轻 (重), 表现为08 :00、14 :00、20 :00能见度与SO2浓度负相关; 总云量越多, 往往是大气对流强烈, 或有雨、雪, 或风速大, SO2浓度低, 表现为总云量与SO2浓度负相关。以上分析表明, SO2浓度与预报因子的正、负相关均与SO2的扩散、稀释的物理过程相符, 说明这些预报因子的选择能反映SO2浓度变化的实际, 是合理的。
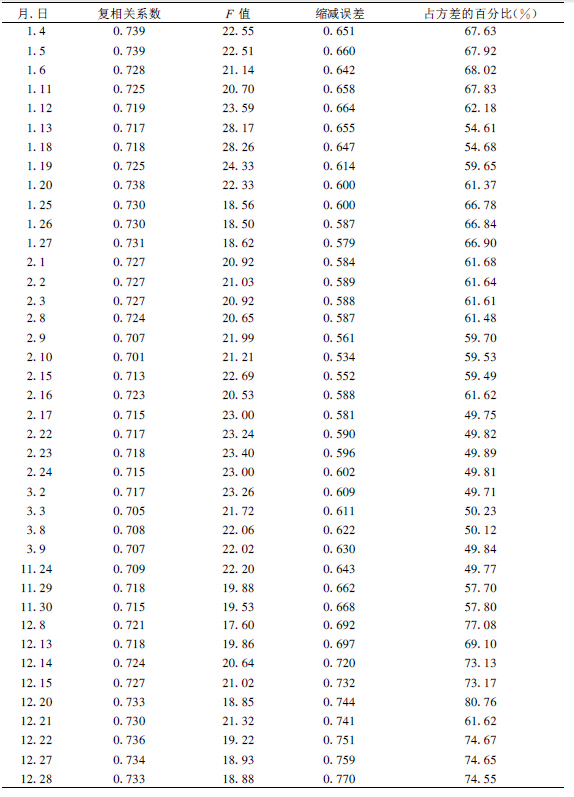
对上述14个因子组成的向量矩阵进行自然正交展开, 把它们分解为14个独立变量组成的列向量, 再以α=0.05的信度, 即F1=F2=1.7, 作为挑选和剔除因子的依据, 进行逐步回归分析, 建立预报模型。在资料的使用上, 随着预报模型改变, 不断滚动加入新一天的资料, 同时去掉最老的一天的资料, 再建立下一天的预报模型, 由此建立了一个变系数的滚动预报模型, 预报值采用的资料是没有参加建立模型的独立资料。各天方程中入选的主成分不同, 各统计预报模型的统计特征量见表 1。
|
|
表 1 1999年采暖期滚动预报模型的统计特征量 |
由表 1可知, 预报模型的复相关系数均大于0.7, 在α=0.01置信水平下, F值均远大于2.9, 超过信度99 %的显著性检验, 缩减误差大部分达0.6以上, 最大达到0.77, 由此可知, 建立的滚动预报模型是显著的、可信的, 可以用来做预报。从预报模型选取因子场的特征量可知, 污染物浓度大部分能够响应因子的60 %以上, 个别可达80 %以上, 表明预报因子的信息量较多。
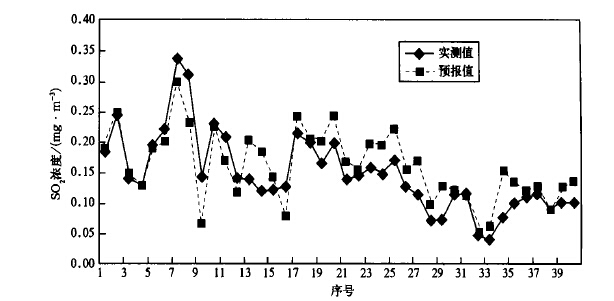
经过40天的预报, SO2浓度的预报结果与实测值对比如图 1所示, 由图 1可知, 两者趋势基本一致。
|
|
| 图 1. 采暖期SO2浓度预报值与实测值对比图 | |
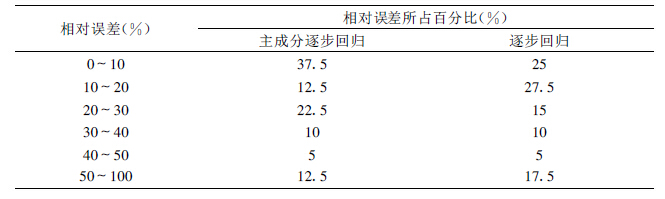
表 2为采暖期主成分逐步回归建立SO2浓度预报模型预报结果与不经过自然正交, 直接使用逐步回归建立预报模型的预报结果的比较。
|
|
表 2 逐步回归与主成分逐步回归SO2浓度预报结果相对误差的比较 |
由表 2可知, 新方法建立的预报模型的预报结果相对误差较小, 精确度也较高, 说明本文的方法有一个比较好的改进。
2.2.2 夏季同理, 分别对上文所选预报因子与SO2浓度进行一元线性回归分析, 在信度α=0.1下, 对因子进行筛选, 得到显著性线性相关的因子有:前一日的日均浓度 (复相关系数0.440)、当日平均气压 (复相关系数-0.282)、当日与前一日温差 (复相关系数0.300)、前一日最高气温 (复相关系数0.267)、当日日均气温 (复相关系数0.348)、当日最高气温 (复相关系数0.447)、当日日照时数 (复相关系数0.343)、当日辐射 (复相关系数0.491)、当日降水 (复相关系数-0.178)、当日总云量 (复相关系数-0.455)、当日14 :00能见度 (复相关系数0.315)、当日20 :00能见度 (复相关系数0.306)。同理分析所选择的预报因子与SO2浓度的线性相关性可知, 所选因子是合理的。以α=0.05置信水平来作为选入和剔除因子的依据, 建立滚动预报模型如下 (预报值采用的资料是没有参加建立模型的独立资料), 各天方程中入选的主成分也不同。预报模型的统计特征量分析及预报结果可知滚动预报模型复相关系数均超过0.6, F值也超过信度99 %的显著性检验, 预报场的信息量变化较大, 有的达80 %以上, 有的则只有50 %左右, 缩减误差超过0.4。预报级别与实测级别都一致, 对级别预报能力很好, 但有的预报值的相对误差较大, 这主要是因为SO2浓度最大值0.047 mg/m3与最小值0.002 mg/m3之间相差较大, 达到20多倍。
3 结束语本文针对统计预报方法的不足, 把一元线性回归分析、自然正交分解 (EOF) 和逐步回归方法结合起来, 建立变量之间相互独立的滚动的统计预报模型。通过预报试验, 采暖期预报的级别命中率为72.5 %, 夏季级别预报命中率为100 %, 具有较好的预报能力。通过比较试验此方法优于目前常用的逐步回归方法, 有很好的应用前景。
本文改进的方法, 已程序化, 可在计算机上运行。通过更新数据库、给定显著性水平, 可进行准自动滚动预报, 能够投入业务应用。
由于统计方法的前提是假设污染源及其排放量是不变的, 故本文采用滚动法截去前期资料, 使用近三年的资料建立预报方程, 使污染源及其排放量尽可能保持相对不变。但因为小概率事件需要从大量的历史样本得到信息才有可能进行预报, 所以本方法对极值或小概率事件很难预报出来。
本文的预报方法虽有所改进, 但仍有不足, 如没有考虑系统的非线性, 与其它统计方法一样, 对奇异值预报效果差。空气污染预报在我国也正处于发展时期, 还有许多工作要做, 本研究还是初步的, 有待于进一步完善。
| [1] | 蒋维楣, 曹文俊, 蒋瑞宾. 空气污染气象学教程. 北京: 气象出版社, 1993. |
| [2] | 李宗凯, 潘云仙, 孙涧桥. 空气污染气象学原理及应用. 北京: 气象出版社, 1985. |
| [3] | 洪钟祥, 胡非. 大气污染预测的理论和方法研究进展. 气候与环境, 1999, 4, (3): 226–230. |
| [4] | 雷孝恩, 张美根, 韩志伟, 等. 大气污染数值预报基础. 北京: 气象出版社, 1998. |
| [5] | 项静恬, 史久恩. 非线性系统中数据处理的统计方法. 北京: 科学出版社, 1997. |
| [6] | 苏炳凯. 大气科学中的统计诊断与预测. 南京: 南京大学出版社, 1988. |
| [7] | 吴祥定. 树木年轮与气候变化. 北京: 气象出版社, 1990. |
 2003, 14 (2): 223-229
2003, 14 (2): 223-229