2. 中国科学院地理科学与资源研究所, 北京 100101
2. nstitute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101
目前, 针对IPCC第3次评估报告[1]中的近千年温度变化曲线, 国内外还存在争论。由于20世纪50年代以前中国器测气象资料较为缺乏, 使得相关方面的研究更为迫切, 需要从更多方面研究历史时期不同区域的气候变化特征, 以了解历史上所发生的真实的气候变化。
树木年轮学 (Dendrochronology) 是一门以植物生理学为基础, 以树木年轮生长特性为依据, 研究环境对年轮生长影响的学科, 旨在获取代用资料, 重建环境因子的变化史实[2]。鉴于树木年轮资料具有定年准确、连续性强、分辨率高和易于获取复本等特点, 树木年轮分析长期以来在地球科学界受到了高度的重视[3], 在过去全球变化研究中, 被列为重要的技术途径之一①, 在历史时期气候变化研究中得到了广泛的应用[4-6]。
①ICSU.IGBP Report No.19.PAGES Past Global Changes Project :Proposed Implementation Plans for Research Activities.Edit ed by Eddy J A, 1992.1~112pp.
秦岭横亘于我国中部, 山脉以北气候相对干燥, 属暖温带亚湿润气候区; 山脉以南气候温暖湿润, 属北亚热带湿润气候区。秦岭被认为是我国气候划分上的一条重要分界线, 是我国气候变化的敏感区域[7]。秦岭地区为我国东部季风区的组成部分, 季风影响显著, 风向和降水均随季节的变化而存在明显的交替[8]。尤其是盛夏季节气流由南向北翻越秦岭山脉时, 在南坡地区导致较多的降水[7], 一般年降水量在800 mm以上, 尤其是位于山地2000~2500 m高度附近, 通常存在一个最大降雨带, 年降雨量可达1000 mm左右[9]。
邵雪梅等[10, 11]根据秦岭东端华山采集的华山松样本建立了3种树木年轮年表, 分析了树木生长对气候变化的响应关系, 认为华山松的生长主要受当年4月温度和4~7月 (特别是5~6月) 降水的影响, 与6月温度同样具有密切的关系, 并重建了华山4~7月降水; 刘洪滨等[12]根据华山的树轮年表重建了中国中北部地区1500年以来的干燥指数; 吴祥定等[13, 14]根据秦岭地区华山、太白、佛坪和镇安等样点前期建立的树轮年表, 分析了年轮宽度年表以及年轮密度年表对气候变化的响应, 得出“多数情况下, 年轮密度年表所包含的气候信息量可能高于宽度年表”的结论; 刘洪滨等[15]及刘禹等[16]根据秦岭南坡镇安地区的秦岭冷杉树轮年表, 重建了当地历史时期的初春温度序列, 并对重建结果进行了周期及突变分析。
本文采用秦岭南坡佛坪地区多个样点的树木年轮宽度和密度年表, 分析年表与气候要素变化的关系, 在此基础上重建佛坪历史时期相关气候要素的变化, 并对其变化特征进行分析。
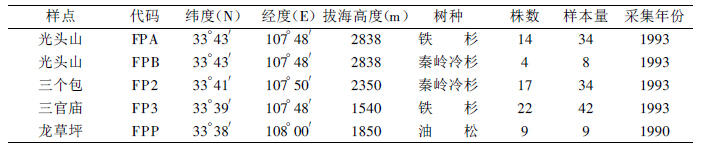
1 资料佛坪地区树木年轮样本的采集时间分别为1990年和1993年夏季 (见表 1), 样点为地属陕西佛坪县的龙草坪、光头山、三个包和三官庙, 树种包括油松 (Pinus tabulaeformis Carr.)、秦岭冷杉 (Abies chensiensis Van Tieg hem) 和铁杉 (Tsuga chinensis Beisen), 树木生长状况良好, 土壤湿润, 有机质含量丰富, 郁闭度约在0.4~0.6之间, 坡度约在10°~60°之间, 树木生长较少受到人为影响。
|
|
表 1 秦岭南坡佛坪地区树轮样点 |
按照树木年轮样本的基本处理程序[17], 对样本进行前期处理、交叉定年及定年检验。考虑到树木自身遗传作用导致的生长趋势以及树木间的生长竞争等非气候因子在年轮宽度序列中的反映, 采用样条函数进行生长趋势拟合、去趋势订正、自回归模型拟合、去持续性波动等过程对样本序列进行了标准化, 并最终分别建立了3种树木年轮年表, 即标准化年表 (STD)、差值年表 (RES) 和自回归年表 (ARS)。鉴于佛坪各样点树木生长受外界因子影响较为复杂, 样条函数的步长一般较短, 多数步长取在10年以下。
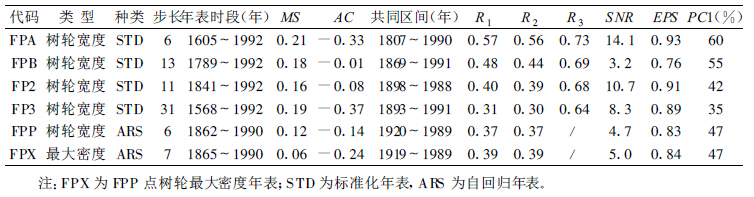
表 2为选用年表的统计参数以及共同区间分析部分结果, 其中包括:敏感度 (MS)、自相关系数 (AC)、样本间平均相关系数 (R1)、不同树木样本间平均相关系数 (R2)、同棵树木样本间平均相关系数 (R3)、信噪比 (SNR)、样本对总体的解释信号 (EPS)、以及第一主分量所占的方差百分比 (PC1)。共同区间分析选取去趋势序列相应统计参数。
|
|
表 2 佛坪地区树轮年表统计参数及共同区间分析 |
气候资料为陕西佛坪站 (33°32′N, 107°59′E, 拔海高度约1192 m) 月平均温度和月降水量资料序列 (见图 1)。分别采用Mann-Kandell方法[18]和Double-massanaly sis方法[19]检验气候序列的一致性。结果表明, 佛坪站月平均温度和月降水量资料能够较好地满足一致性要求, 可被认为代表了自然界的气候变化。
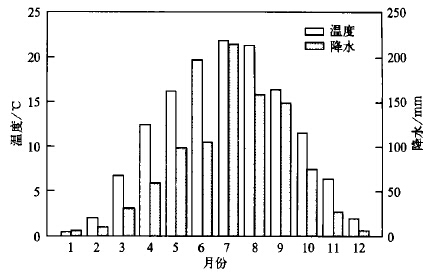
|
|
| 图 1. 佛坪各月月平均气温和月降水量 (1957~1992年) | |
佛坪站年降水量大于900 mm, 7~9月降水量占全年的50 %以上, 7月降水量最多, 平均高于210 mm; 年平均温度为11.4 ℃, 其中4~10月月平均温度大于10 ℃。
2 结果与分析 2.1 相关函数及响应函数定义在采用树轮年表对历史时期气候变化进行重建前, 首先应确定树木生长与气候要素变化的响应关系, 响应关系的好坏将直接影响到重建过程的稳定性, 并影响重建结果的可信度。本文采用相关函数 (Correlation Function) 与响应函数 (Response Function) 方法[20]分析树木生长与气候变化的关系, 其中相关函数即树轮年表与各月气候要素序列的相关系数, 响应函数的具体计算方法如下:
设C为以树轮年表为横向量的矩阵, M为以p个气候要素标准化向量为横向量的矩阵, C以及M中各序列的长度均为n, 得到回归方程
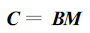
|
(1) |
其中B为系数矩阵。由于气候要素向量为标准化向量, B中各值的大小反映不同气候要素对树木生长的影响程度。
由于在不同气候要素以及相同气候要素不同月之间存在一定的相关性, 会造成B中各值大小与实况不符, 因此需要进行处理。计算M中标准化向量的主分量, 得到以p个主分量为横向量组成的矩阵P, 即

|
(2) |
其中V为以矩阵MM′的特征向量为列向量的矩阵。以P中各主分量为自变量, 以年表序列为因变量, 进行逐步回归, 回归方程为

|
(3) |
其中B1为回归系数矩阵, 将B1中“非显著”系数附值为0, 得到B1*。将式 (2) 代入式 (3), 并令B2=B1* V′, 得到回归方程
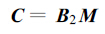
|
(4) |
其中B2为对应于M中各气候要素标准化向量的回归系数矩阵。经上述变换, B2中各值可被认为较真实地反映了树木生长对气候要素变化的响应。B2中各回归系数越大, 则说明相应的气候要素序列对树木生长的影响越显著, 因而称B2中各值为响应函数。
2.2 佛坪地区树木生长对气候变化的响应分别计算佛坪地区5个样点树轮年表与气候要素间的相关函数和响应函数。表 3中所列为各树轮年表与当年1~9月各月平均温度相关函数及响应函数分析的部分结果。其中黑体表示相应的相关函数超过0.05置信水平, 下划线表示相应的响应函数超过0.05置信水平; R 2为响应函数分析中温度和降水变化对树木生长的方差解释量; F为方程显著性检验值; p为显著水平。
|
|
表 3 佛坪树轮年表与月平均温度间的相关函数及响应函数分析结果 |
从相关函数分析结果可见, 大多数年表与1~4月月平均温度有较为明显的正相关关系, 其中FPASTD年表、FPBSTD年表、FPPARS年表以及FPXARS年表与当年2月月平均温度序列的相关系数达到或超过0.05置信水平。另外, 年表FP2STD、FP3STD以及FPBSTD分别与4月、5月和7月月平均温度序列的相关系数也达到或超过0.05置信水平。计算各年表与1~4月平均温度序列的相关系数发现, 除与FP3STD年表对应的相关系数置信水平为0.07外, 其它年表所对应的相关系数均接近或超过0.01置信水平。
从响应函数分析结果看, 回归方程的解释方差量以FPASTD年表最大, 为64 %, FPXARS的解释方差量最小, 为22 %, 而回归方程的显著性均超过了90 %。
相同样点不同树种对气候变化的响应也表现不同。如FPA和FPB两样点均为佛坪县光头山, 采样高度相同, 树木所处的生态环境相同, 而树种分别为铁杉和冷杉。从相关函数和响应函数分析结果来看, 二者虽大体相似, 但在细节上依然存在一定的差别。
产生上述分析结果是由于该地区树木的活跃生长期一般大致在4~9月[10, 15], 前期温度的高低将直接影响树木生长期开始的早晚, 前期温度较高使得树木形成层的细胞分裂早, 有利于树木生长期的提前, 从而在客观上使生长期延长, 形成较宽的年轮。随着温度的不断升高以及降水的不断增加, 树木生长所需要的温度和湿度条件能够得到充分的满足, 使得这两种气候因子不再成为树木生长的限制性因子, 表现为树轮年表与温度和降水的关系不明显。
2.3 佛坪1~4月平均温度重建根据佛坪地区树木生长与气候变化关系的分析, 选取与佛坪1~4月平均温度资料关系较好的6个树轮年表, 对佛坪地区1~4月平均温度变化进行重建。
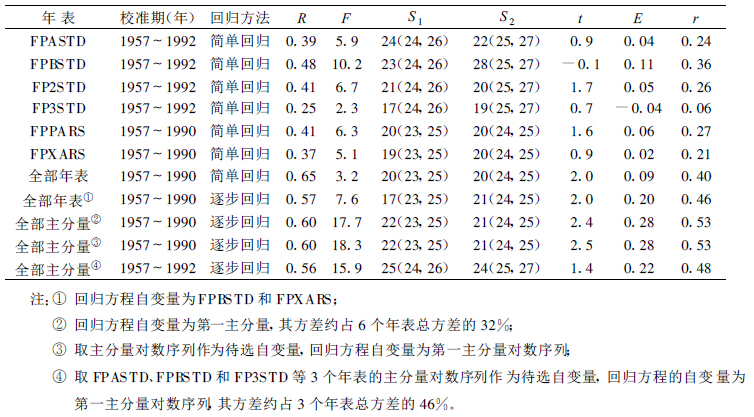
首先采用各样点年表与温度序列建立回归方程, 比较各重建方程的统计参数差异, 然后采用主分量分析方法得到这些年表的主分量, 并用主分量作为自变量建立回归方程。采用“逐一剔除法”[21]对回归方程的稳定性进行检验。检验方法包括4种:符号检验、乘积平均值检验、误差缩减和相关系数[22] (见表 4)。
|
|
表 4 佛坪1~4月平均温度重建结果统计参数比较 |
表 4中R为回归方程的复相关系数, 其平方 (R2) 即为回归方程的方差解释量, 代表树轮年表对温度变化的拟合程度, 取值范围在[0, 1]之间, 值越大, 说明方程的拟合程度越高; F值大小反映了回归方程的显著性程度, F值越大, 表示回归系数为0的可能性越小, 回归方程越显著。S1为重建序列与实测序列的一阶差值同号数, S2为重建序列与实测序列相对于实测序列平均值差值的同号数, 随后括号中分别为相应的95 %和99 %置信度临界值; t为乘积平均值检验值; E为误差缩减值; r为校准序列与实测序列间的相关系数值。
需要说明的是, 由于FPP点的年表 (FPPARS和FPXARS) 较短, 重建序列仅126年 (1865~1990年), 因此采用FPASTD、FPBSTD和FP3STD等3个较长的年表重建1865年以前的1~4月平均温度序列, 从而能够使重建序列得到有效的延长。
在单个树轮年表的重建结果中, 以FPBSTD年表的重建结果与实测序列最为吻合, 各项参数较其它年表为高, 其中S2值超过了99 %置信度。将6个年表全部作为自变量, 采用逐步回归方法, 建立回归方程, 其重建结果的可靠性和稳定性均有较大幅度的提高, 重建序列与实测序列的相关系数达到0.57, F值为7.6, 校准序列与实测序列的相关系数达到0.46, 而E值也提高到0.20, 说明运用多个年表的重建效果要比单个年表更为接近实测序列。
主分量分析方法的引用可使重建结果的可靠性和稳定性进一步提高, 而取主分量对数序列作为自变量建立回归方程所得到的重建结果的各项统计参数也有所加大。在重建结果的统计参数中可见, 重建序列与实测序列的相关系数提高到0.60, F值高达18.3, 而校准序列与实测序列的相关系数达到0.53, t值达到2.5, E值提高到0.28, 这些参数在所有重建过程中为最高。说明主分量分析方法及对数序列的引用在佛坪地区1~4月平均温度序列的重建过程中是有效的。
采用FPASTD、FPBS TD和FP3STD等3个年表的主分量对数序列作为自变量进行回归分析, 其结果略逊于由6个年表的主分量对数序列所建立的重建方程, 但此重建方程也同样具有很高的稳定性。从各项统计参数上看, 方程的复相关系数也达到了0.56, F值高达15.9, 超过0.01置信水平, 其它统计参数取值也同样较大。在1957~1990年时间段内两次重建结果间的相关系数为0.76, 在1865~1990年时间段内的相关系数为0.65, 且经验证两条序列之间不存在显著的均值和方差差异, 因此可以认为重建结果满足延长重建序列的需要。
将上述两次重建结果组合在一起, 得到1789~1992年长度为204年的佛坪1~4月平均温度重建序列。
从图 2a中可以看出, 总体上采用树轮年表重建的佛坪1~4月平均温度序列, 能够与实测温度序列较好地吻合, 但重建序列与实测序列的年际变化在某些时段存在较大的差异, 可能是由于多种因子同时作用于树木生长的结果。
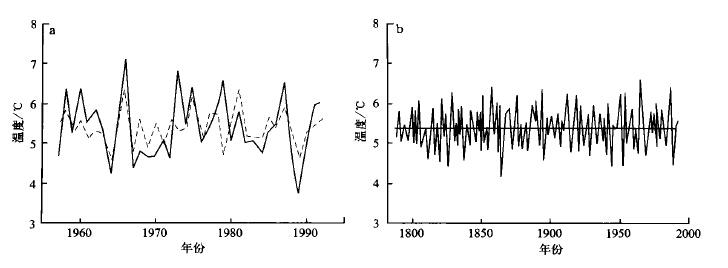
|
|
| 图 2. 重建值 (虚线) 与实测值 (实线) 比较 (1957~1992年)(b) 重建值序列 (1789~1992年) | |
另外, 图 2b中1~4月平均温度曲线的变化表明, 佛坪1~4月平均温度变化相对较为平稳, 这种现象与临近的镇安的初春温度重建结果不符, 其中部分原因是由于去趋势过程中样条函数步长较小, 从而人为地去除了树木生长中的低频变化部分, 导致了重建结果无法反映该地1~4月平均温度的低频变化。但正如前面提到, 佛坪地区各样点树木生长的影响因素较为复杂, 使得不同样本序列中所反映的低频变化各不相同, 无法有效地分清低频部分中哪些属于气候变化, 而哪些又是非气候因子作用的结果。
2.4 佛坪历史时期1~4月平均温度变化特征基于佛坪1~4月平均温度变化的重建结果, 分析重建序列变化的周期和突变特征。采用功率谱[23]对重建序列进行周期分析, 以了解在较长时间范围内佛坪1~4月平均温度变化的周期性 (见图 3)。序列长度为204年, 功率谱分析中最大后延数取68, 相当于序列长度的三分之一, 相应的图中横坐标为波数, 纵坐标为功率谱值, 当功率谱大于一定置信水平所对应的临界值时, 则认为相应周期显著。
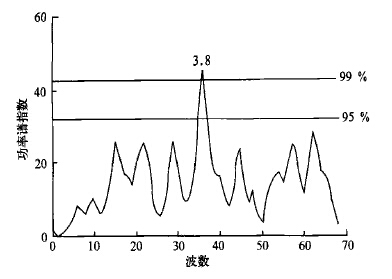
|
|
| 图 3. 佛坪1~4月平均温度变化周期分析 | |
由图 3可见, 19世纪中期以来, 佛坪地区1~4月平均温度变化存在明显的周期特征, 以3.8年的周期最为显著, 功率谱值超过99 %置信度临界值。鉴于样本序列标准化过程中样条函数步长很小, 重建序列中不包含更长时间尺度的周期变化。
采用滑动t检验法[24]、滑动F检验法[24]以及Lepage检验法[25]对重建序列进行突变检验分析 (见图 4)。其中滑动t检验法用于检验均值突变, 滑动F检验法用于检验方差突变, 而Lepage检验法对序列中存在的均值和方差突变均具有一定的检验效力。检验过程的时间尺度均取10年, 当检验值大于某置信水平所对应的临界值时, 则认为序列中相应两个10年之间存在显著差异, 即该地区气候可能存在突变。
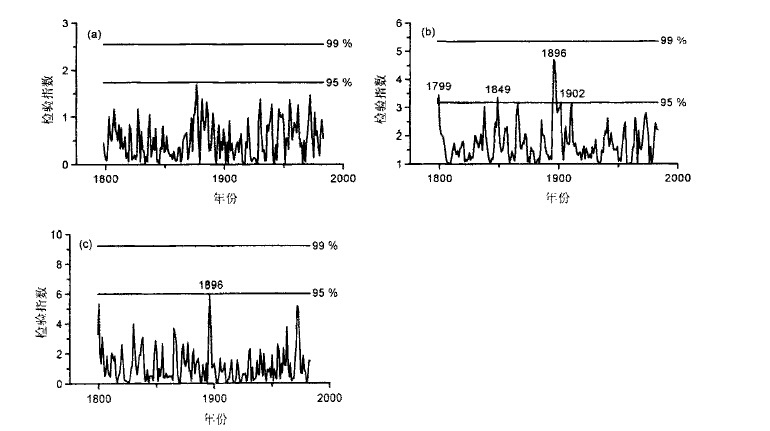
|
|
| 图 4. 佛坪1~4月平均温度变化突变分析 (1798~1983年)(a) 滑动t检验, (b) 滑动F检验, (c) Lepage检验 | |
滑动F检验法和Lepage检验法计算结果均明显地反映出佛坪地区1789年以来在1896年前后出现了10年尺度的显著的方差突变, 其置信度超过95 %, 其它可能存在的方差突变年份为1799年、1849年和1902年。但上述方法未检验出明显的均值突变。通过分析重建的温度序列 (见图 2b), 佛坪1~4月平均温度在突变点前后确实存在着波动幅度的变化。
以上周期分析及突变分析结果是否确实, 还需有关资料的进一步印证。
3 结论(1) 佛坪地区树木生长的前期温度在一定的程度上影响当年的树木生长, 表现为树轮年表指数大小与当年1~4月平均温度变化呈显著的正相关关系;
(2) 利用佛坪地区多个样点、多种类型的树轮年表进行1~4月平均温度变化重建, 并将主分量分析方法引入重建过程, 可以大幅度提高重建方程的显著性和稳定性, 从而有效地提高重建结果的可信度;
(3) 佛坪1~4月平均温度变化存在明显的3~4年周期, 其置信度超过99 %;
(4) 18世纪后期以来, 佛坪1~4月平均温度于1896年前后出现了10年尺度的突变, 表现为温度波动幅度的变化。
| [1] | Houghton J T, Ding Y, Griggs D J, et al.Climate Change 2001 :The Scientific Basis.Cambridge:Press Syndicate of Cambridge University, 2001. |
| [2] | 吴祥定. 树木年轮分析在环境变化研究中的应用. 第四纪研究, 1990, 10, (2): 188–196. |
| [3] | 吴祥定, 邵雪梅. 中国树木年轮气候学研究动态与展望. 地球科学进展, 1993, 8, (6): 31–35. |
| [4] | Fritts H C.Reconstruction Large-scale Climate Patterns from Tree-Ring Data.Arizona:University of Arizona Press, 1991. |
| [5] | Gambetti D, Lo Vecchio G, Nanni T, et al. Climate and site dependence of the annual growth of silver fir (Abies albaMiller) in the Northern Apennines, Italy. Geophysics and Space Physics, 2000, 23C, (2): 111–131. |
| [6] | Gervais B R, MacDonald G M, A 403-year record of July temperatures and treeline dynamics of Pinus sylvestris from the Kola Peninsula, northwest Russia. Arctic, Antarctic, and Alpine Research, 2000, 32, (3): 295–302. DOI:10.2307/1552528 |
| [7] | 陈明荣. 秦岭的气候与农业. 陕西: 陕西人民出版社, 1983. |
| [8] | 聂树人. 陕西自然地理. 陕西: 陕西人民出版社, 1981. |
| [9] | 李兆元, 傅抱璞. 秦岭山地的气候特点山地气候文集. 北京: 气象出版社, 1984: 87-97. |
| [10] | 邵雪梅, 吴祥定. 华山树木年轮年表的建立. 地理学报, 1994, 49, (2): 174–181. |
| [11] | Hughes M K, Wu X D, Shao X M, et al. A preliminary reconst ruction of rainfall in North-Central China since A.D.1600 from tree-ring density and width. Quaternary Research, 1994, 42: 88–99. DOI:10.1006/qres.1994.1056 |
| [12] | 刘洪滨, 邵雪梅, 黄磊. 中国陕西关中及周边地区近500年来初夏干燥指数序列的重建. 第四纪研究, 2002, 22, (3). |
| [13] | Wu X D, Tree-ring width chronologies and their response to climate in the Qinling Mountains, China.Terres.Atoms. Oceanic Sci, 1994, 5, (3): 365–372. |
| [14] | 吴祥定, 邵雪梅. 中国秦岭地区树木年轮密度对气候响应的初步分析. 应用气象学报, 1994, 5, (2): 253–256. |
| [15] | 刘洪滨, 邵雪梅. 采用秦岭冷杉年轮宽度重建陕西镇安1755年以来的初春温度. 气象学报, 2000, 58, (2): 223–233. |
| [16] | 刘禹, 马利民, 蔡秋芳, 等. 依据陕西秦岭镇安树木年轮重建3-4月份气温序列. 自然科学进展, 2001, 11, (2): 157–162. |
| [17] | Stocks, M, Smiley T.An Introduction to Tree-ring Dating.Chicago :University of Chicago Press, 1968. |
| [18] | Mann H B, Non-parametric test against trend. Econometrika, 1945, 13: 245–259. DOI:10.2307/1907187 |
| [19] | Kohler M A, On the use of double-mass analysis for testing the consistency of meteorological records and for makingrequired adjustment. Bulletin of the American Meteorologi cal Society, 1949, 30: 188–189. |
| [20] | Fritts H C, Tree Rings and Climate. London: Academic Press Incorporation, 1976. |
| [21] | Walpol R E, Myers R H, Probability and Statistics for Engineers and Scientist s. New York: Macmillan Publishing Company, 1985. |
| [22] | 尹训钢, 刘洪滨, 邵雪梅. 用树木年轮重建过去气候模型程序的流程分析.气候变化规律及其数值模拟研究论文 (第一集).. 北京: 气象出版社, 1996: 116-126. |
| [23] | 黄嘉佑. 气象中的谱分析. 北京: 气象出版社, 1984. |
| [24] | 刘洪滨. 秦岭地区三百年来的气候变化:. 北京:中国科学院国家计委地理研究所, 1996. |
| [25] | Yanetani T, Discontinuous changes of precipitation in Japanafter 1900 detected by the Lepage test. Journal of Meteorological Society of Japan, 1992, 70, (1): 95–103. |
 2003, 14 (2): 188-196
2003, 14 (2): 188-196